总体最小二乘同时考虑了系数矩阵和观测向量的误差，理论严密，受到广泛关注。目前，总体最小二乘已经被应用到各个方面。文献[1-2]针对线性回归，推导了总体最小二乘算法，考虑了自变量误差和系数矩阵中常数项；文献[3]推导了结构总体最小二乘，应用于自回归模型中，可以保证不同位置的相同元素有相同的改正数；文献[4]同样对自回归模型推导了一种新总体最小二乘方法，可以起到结构总体最小二乘一样的作用; 文献[5]将总体最小二乘应用到三维基准转换中；文献[6]将混合总体最小二乘应用到三维基准转换，并附加了约束条件；文献[7]推导了三维基准转换的总体最小二乘拟合推估，将求解坐标转换参数和非公共点坐标同时进行；文献[8]推导了附加约束条件的总体最小二乘，可用于大旋转角的三维坐标转换，但计算过于繁琐，存在系数矩阵含有常数和某些元素重复出现问题；文献[9]将多元总体最小二乘用于大旋转角的三维坐标转换，可以避免上述问题；此外，总体最小二乘还被应用到其他方面，针对不同的情况，学者们对总体最小二乘进行了不同的改进。

文献[10-11]推导了非线性总体最小二乘算法，当系数矩阵的元素不再是自变量本身，而是通过自变量计算得到，即是关于自变量的函数，将这种情况下的总体最小二乘平差称为非线性总体最小二乘平差，如GPS高程拟合。但以上都是针对非线性形式出现在系数矩阵的情况，而在球面拟合当中，非线性形式出现在观测向量中，并且系数矩阵中存在无误差的常数项和重复元素。为此，本文推导了一种改进的总体最小二乘算法来克服上述问题。

1 球面拟合

球面拟合是根据一定数量的球面点来求得球心坐标和球半径的过程，球面方程为:

$ {r^2} = {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} $

(1)

式中，(a，b，c)为球心坐标，r为球半径，(x, y, z)为球面上点的坐标。

将球面方程展开得：

$ \begin{array}{*{20}{c}} {{x^2} + {y^2} + {z^2} = }\\ {2xa + 2yb + 2zc + {r^2} - {a^2} - {b^2} - {c^2}} \end{array} $

(2)

将式中a、b、c、r²-a²-b²-c²看作待估参数，当观测获得n个球面点时，则有：

$ \begin{array}{*{20}{c}} {\underbrace {\left[ {\begin{array}{*{20}{c}} {2{x_1}}&{2{y_1}}&{2{z_1}}&1\\ {2{x_2}}&{2{y_2}}&{2{z_2}}&1\\ \vdots&\vdots&\vdots&\vdots \\ {2{x_n}}&{2{y_n}}&{2{z_n}}&1 \end{array}} \right]}_\mathit{\boldsymbol{A}}\underbrace {\left[ {\begin{array}{*{20}{c}} a\\ b\\ c\\ {{r^2} - {a^2} - {b^2} - {c^2}} \end{array}} \right]}_\mathit{\boldsymbol{X}} = }\\ {\underbrace {\left[ {\begin{array}{*{20}{c}} {x_1^2 + y_1^2 + z_1^2}\\ {x_2^2 + y_2^2 + z_2^2}\\ \vdots \\ {x_n^2 + y_n^2 + z_n^2} \end{array}} \right]}_\mathit{\boldsymbol{Y}}} \end{array} $

(3)

式中，A为系数矩阵，Y为观测向量，X为待估参数。

采用最小二乘求解，得：

$ \mathit{\boldsymbol{\hat X = }}{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $

(4)

观察系数矩阵和观测向量不难发现，球面拟合中系数矩阵亦是由坐标组成的，同样含有误差，此时采用最小二乘求解并不合理，而应采用总体最小二乘求解。但是系数矩阵和观测向量的误差同源，增广矩阵[A Y]中不同位置有相同的元素存在，并且非线性形式出现在观测向量中，这些在求解球面拟合时都是需要考虑的，此时传统的总体最小二乘也不再合适。

2 改进的总体最小二乘算法

根据文献[10-11]非线性总体最小二乘的思路，非线性总体最小二乘问题可以看作是一个双非线性问题，可以通过两次线性化的方法获得非线性总体最小二乘的解：一次是在系数矩阵中的随机元素初值处线性化，一次是在参数估值的初值处线性化。

在球面拟合中，非线性形式出现在观测向量中，因此根据式(2)对观测向量中的随机元素线性化，即在球面点坐标(x⁰, y⁰, z⁰)处线性化，舍弃二阶极小项，整理得：

$ \begin{array}{*{20}{c}} {2{x^0}\Delta x - 2a\Delta x + 2{y^0}\Delta y - 2b\Delta y + 2{z^0}\Delta z - }\\ {2c\Delta z - 2a{x^0} - 2b{y^0} - 2c{z^0} + }\\ {{a^2} + {b^2} + {c^2} - {r^2} = - {{\left( {{x^0}} \right)}^2} - {{\left( {{y^0}} \right)}^2} - {{\left( {{z^0}} \right)}^2}} \end{array} $

(5)

将上式对参数估值线性化，即在a⁰、b⁰、c⁰、r⁰处线性化，同样舍弃二阶极小项，整理得：

$ \begin{array}{*{20}{c}} {\left( {2{x^0} - 2{a^0}} \right)\Delta x + \left( {2{y^0} - 2{b^0}} \right)\Delta y + \left( {2{z^0} - 2{c^0}} \right)\Delta z = }\\ {\left( {2{x^0} - 2{a^0}} \right)\Delta a + \left( {2{y^0} - 2{b^0}} \right)\Delta b + \left( {2{z^0} - 2{c^0}} \right)\Delta c + }\\ {2{r^0}\Delta r - \left( {{{\left( {{x^0}} \right)}^2} + {{\left( {{y^0}} \right)}^2} + {{\left( {{z^0}} \right)}^2} + {{\left( {{a^0}} \right)}^2} + {{\left( {{b^0}} \right)}^2} + } \right.}\\ {\left. {{{\left( {{c^0}} \right)}^2} - {{\left( {{r^0}} \right)}^2} - 2{a^0}{x^0} - 2{b^0}{y^0} - 2{c^0}{z^0}} \right)} \end{array} $

(6)

假设有n个球面点，则可以得到：

$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\left( {2x_1^0 - 2{a^0}} \right)\Delta {x_1} + \left( {2y_1^0 - 2{b^0}} \right)\Delta {y_1} + \left( {2z_1^0 - 2{c^0}} \right)\Delta {z_1}}\\ {\left( {2x_2^0 - 2{a^0}} \right)\Delta {x_2} + \left( {2y_2^0 - 2{b^0}} \right)\Delta {y_2} + \left( {2z_2^0 - 2{c^0}} \right)\Delta {z_2}}\\ \vdots \\ {\left( {2x_n^0 - 2{a^0}} \right)\Delta {x_n} + \left( {2y_n^0 - 2{b^0}} \right)\Delta {y_n} + \left( {2z_n^0 - 2{c^0}} \right)\Delta {z_n}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {2x_1^0 - 2{a^0}}&{2y_1^0 - 2{b^0}}&{2z_1^0 - 2{c^0}}&{2{r^0}}\\ {2x_2^0 - 2{a^0}}&{2y_2^0 - 2{b^0}}&{2z_2^0 - 2{c^0}}&{2{r^0}}\\ \vdots&\vdots&\vdots&\vdots \\ {2x_n^0 - 2{a^0}}&{2y_n^0 - 2{b^0}}&{2z_n^0 - 2{c^0}}&{2{r^0}} \end{array}} \right]} {\left[ {\begin{array}{*{20}{c}} {\Delta a}\\ {\Delta b}\\ {\Delta c}\\ {\Delta r} \end{array}} \right] - \\ \left[ {\begin{array}{*{20}{c}} {{{\left( {x_1^0} \right)}^2} + {{\left( {y_1^0} \right)}^2} + {{\left( {z_1^0} \right)}^2} + {{\left( {{a^0}} \right)}^2} + {{\left( {{b^0}} \right)}^2} + {{\left( {{c^0}} \right)}^2} - {{\left( {{r^0}} \right)}^2} - 2{a^0}x_1^0 - 2{b^0}y_1^0 - 2{c^0}z_1^0}\\ {{{\left( {x_2^0} \right)}^2} + {{\left( {y_2^0} \right)}^2} + {{\left( {z_2^0} \right)}^2} + {{\left( {{a^0}} \right)}^2} + {{\left( {{b^0}} \right)}^2} + {{\left( {{c^0}} \right)}^2} - {{\left( {{r^0}} \right)}^2} - 2{a^0}x_2^0 - 2{b^0}y_2^0 - 2{c^0}z_2^0}\\ \vdots \\ {{{\left( {x_n^0} \right)}^2} + {{\left( {y_n^0} \right)}^2} + {{\left( {z_n^0} \right)}^2} + {{\left( {{a^0}} \right)}^2} + {{\left( {{b^0}} \right)}^2} + {{\left( {{c^0}} \right)}^2} - {{\left( {{r^0}} \right)}^2} - 2{a^0}x_n^0 - 2{b^0}y_n^0 - 2{c^0}z_n^0} \end{array}} \right]} \end{array} $

(7)

令$\mathit{\boldsymbol{V}} = \left[{\begin{array}{*{20}{c}} {(2{x^0}_1-2{a^0})\Delta {x_1} + (2{y^0}_1-2{b^0})\Delta {y_1} + (2{z^0}_1-2{c^0})\Delta {z_1}}\\ {(2{x^0}_2 - 2{a^0})\Delta {x_2} + (2{y^0}_2 - 2{b^0})\Delta {y_2} + (2{z^0}_2 - 2{c^0})\Delta {z_2}}\\ \vdots \\ {(2{x^0}_n - 2{a^0})\Delta {x_n} + (2{y^0}_n - 2{b^0})\Delta {y_n} + (2{z^0}_n - 2{c^0})\Delta {z_n}} \end{array}} \right], \delta \mathit{\boldsymbol{\xi }} = \left[{\begin{array}{*{20}{c}} {\mathit{\Delta a}}\\ {\mathit{\Delta }b}\\ {\mathit{\Delta }c}\\ {\mathit{\Delta }r} \end{array}} \right]$$\mathit{\boldsymbol{A}}{^0} = \left[{\begin{array}{*{20}{c}} {2{x_1}^0-2{a^0}}&{2{y_1}^0-2{b^0}}&{2{z_1}^0-2{c^0}}&{2{r^0}}\\ {2{x_2}^0 - 2{a^0}}&{2{y_2}^0 - 2{b^0}}&{2{z_2}^0 - 2{c^0}}&{2{r^0}}\\ \vdots & \vdots & \vdots & \vdots \\ {2{x_n}^0 - 2{a^0}}&{2{y_n}^0 - 2{b^0}}&{2{z_n}^0 - 2{c^0}}&{2{r^0}} \end{array}} \right], \mathit{\boldsymbol{L}}{^0} = $$\left[{\begin{array}{*{20}{c}} {{{({x_1}^0)}^2} + {{({y_1}^0)}^2} + {{({z_1}^0)}^2} + {{({a^0})}^2} + {{({b^0})}^2} + {{({c^0})}^2}-{{({r^0})}^2}-2{a^0}{x_1}^0-2{b^0}{y_1}^0 - 2{c^0}{z_1}^0}\\ {{{({x_2}^0)}^2} + {{({y_2}^0)}^2} + {{({z_2}^0)}^2} + {{({a^0})}^2} + {{({b^0})}^2} + {{({c^0})}^2} - {{({r^0})}^2} - 2{a^0}{x_2}^0 - 2{b^0}{y_2}^0 - 2{c^0}{z_2}^0}\\ \vdots \\ {{{({x_n}^0)}^2} + {{({y_n}^0)}^2} + {{({z_n}^0)}^2} + {{({a^0})}^2} + {{({b^0})}^2} + {{({c^0})}^2} - {{({r^0})}^2} - 2{a^0}{x_n}^0 - 2{b^0}{y_n}^0 - 2{c^0}{z_n}^0} \end{array}} \right]$, 则式(7)可以变为：

$ \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{A}}^0}\delta \mathit{\boldsymbol{\xi }} - {\mathit{\boldsymbol{L}}^0} $

(8)

将各点球面坐标提取出来组成列向量：

$ \mathit{\boldsymbol{l}} = {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_n}}&{{y_1}}&{{y_2}}& \cdots &{{y_n}}&{{z_1}}&{{z_2}}& \cdots &{{z_n}} \end{array}} \right]^{\rm{T}}} $

(9)

同时用e_l表示各点坐标误差改正数组成的列向量：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_l} = \left[ {\begin{array}{*{20}{c}} {\Delta {x_1}}&{\Delta {x_2}}& \cdots &{\Delta {x_n}}&{\Delta {y_1}}&{\Delta {y_2}}& \cdots \end{array}} \right.}\\ {{{\left. {\begin{array}{*{20}{c}} {\Delta {y_n}}&{\Delta {z_1}}&{\Delta {z_2}}& \cdots &{\Delta {z_n}} \end{array}} \right]}^{\rm{T}}}} \end{array} $

(10)

则有V = B⁰e_l，并且

$ {\mathit{\boldsymbol{B}}^0} = {\left[ {\begin{array}{*{20}{c}} {2x_1^0 - 2{a^0}}&0& \cdots &0\\ 0&{2x_2^0 - 2{a^0}}& \cdots &0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0& \cdots &{2x_n^0 - 2{a^0}}\\ {2y_1^0 - 2{b^0}}&0& \cdots &0\\ 0&{2y_2^0 - 2{b^0}}& \cdots &0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0& \cdots &{2y_n^0 - 2{b^0}}\\ {2z_1^0 - 2{c^0}}&0& \cdots &0\\ 0&{2z_2^0 - 2{c^0}}& \cdots &0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0& \cdots &{2z_n^0 - 2{c^0}} \end{array}} \right]^{\rm{T}}} $

(11)

此时总体最小二乘目标函数为e_l^TP_le_l=min，P_l为坐标观测值的权阵，与式(8)联立得：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{e}}_l^{\rm{T}}{\mathit{\boldsymbol{P}}_l}{\mathit{\boldsymbol{e}}_l} = \min \\ {\mathit{\boldsymbol{B}}^0}{\mathit{\boldsymbol{e}}_l} = {\mathit{\boldsymbol{A}}^0}\delta \mathit{\boldsymbol{\xi }} - {\mathit{\boldsymbol{L}}^0} \end{array} \right. $

(12)

构建拉格朗日方程：

$ \mathit{\Phi }\left( {{\mathit{\boldsymbol{e}}_l},\delta \mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}} \right) = \mathit{\boldsymbol{e}}_l^{\rm{T}}{\mathit{\boldsymbol{P}}_l}{\mathit{\boldsymbol{e}}_l} + 2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{L}}^0} + {\mathit{\boldsymbol{B}}^0}{\mathit{\boldsymbol{e}}_l} - {\mathit{\boldsymbol{A}}^0}\delta \mathit{\boldsymbol{\xi }}} \right) $

(13)

对上式求偏导数并令其等于0：

$ \frac{1}{2}\frac{{\partial \mathit{\Phi }}}{{\partial {\mathit{\boldsymbol{e}}_l}}} = {\mathit{\boldsymbol{P}}_l}{{\mathit{\boldsymbol{\hat e}}}_l} + {\left( {{\mathit{\boldsymbol{B}}^0}} \right)^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = 0 $

(14)

$ \frac{1}{2}\frac{{\partial \mathit{\Phi }}}{{\partial \mathit{\boldsymbol{\lambda }}}} = {\mathit{\boldsymbol{L}}^0} - {\mathit{\boldsymbol{A}}^0}\delta \mathit{\boldsymbol{\xi }} + {\mathit{\boldsymbol{B}}^0}{{\mathit{\boldsymbol{\hat e}}}_l} = 0 $

(15)

$ \frac{1}{2}\frac{{\partial \mathit{\Phi }}}{{\partial \left( {\delta \mathit{\boldsymbol{\xi }}} \right)}} = - {\left( {{\mathit{\boldsymbol{A}}^0}} \right)^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} = 0 $

(16)

通过整理可以得到：

$ \delta \mathit{\boldsymbol{\xi }} = {\left( {{\mathit{\boldsymbol{A}}^{0{\rm{T}}}}{{\left( {{\mathit{\boldsymbol{B}}^0}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{B}}^{0{\rm{T}}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^0}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{0{\rm{T}}}}{\left( {{\mathit{\boldsymbol{B}}^0}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{B}}^{0{\rm{T}}}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^0} $

(17)

$ \mathit{\boldsymbol{\hat \lambda }} = {\left( {{\mathit{\boldsymbol{B}}^0}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{B}}^{0{\rm{T}}}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{A}}^0}\delta \mathit{\boldsymbol{\hat \xi }} - {\mathit{\boldsymbol{L}}^0}} \right) $

(18)

$ {{\mathit{\boldsymbol{\hat e}}}_l} = - {\mathit{\boldsymbol{Q}}_l}{\left( {{\mathit{\boldsymbol{B}}^0}} \right)^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} $

(19)

式中，Q_l= P_l^-1。

总结计算步骤如下：

1) 采用最小二乘计算球心坐标和球半径的初值a⁰、b⁰、c⁰、r⁰，组成初值ξ⁽⁰⁾=[a⁰  b⁰  c⁰  r⁰]^T，将坐标观测值作为坐标初值，组成l⁰=[x₁⁰  x₂⁰ … x_n⁰  y₁⁰  y₂⁰ … y_n⁰  z₁⁰  z₂⁰ … z_n⁰]^T。

2) 构建A⁽ⁱ⁾、B⁽ⁱ⁾、L⁽ⁱ⁾，分别按式(17)和式(19)计算$\delta {\boldsymbol{\hat \xi} ^{(i + 1)}}$和$ \boldsymbol{\hat e}_l^{i + 1}$。

3) 用公式${\mathit{\boldsymbol{\hat \xi }}^{(i + 1)}} = {\mathit{\boldsymbol{\hat \xi }}^{(i)}} + \delta {\mathit{\boldsymbol{\hat \xi }}^{(i + 1)}}, {\mathit{\boldsymbol{l}}^{(i + 1)}} = {\mathit{\boldsymbol{l}}^{(i)}} + \mathit{\boldsymbol{\hat e}}_l^{(i + 1)}$计算新的更新值，重新构建A⁽ⁱ⁺¹⁾、B⁽ⁱ⁺¹⁾、L⁽ⁱ⁺¹⁾。

4) 重复第2)、3)步，直到满足收敛条件为止。

5) 计算单位权方差和参数估值的方差:

$ \hat \sigma _0^2 = \frac{{\mathit{\boldsymbol{\hat e}}_l^{\rm{T}}{\mathit{\boldsymbol{P}}_l}{{\mathit{\boldsymbol{\hat e}}}_l}}}{{n - 4}} $

(20)

$ {\mathit{\boldsymbol{D}}_{\hat \xi }} = \hat \sigma _0^2{\mathit{\boldsymbol{Q}}_{\hat \xi }} = \hat \sigma _0^2{\left( {{\mathit{\boldsymbol{A}}^{\left( i \right){\rm{T}}}}{{\left( {{\mathit{\boldsymbol{B}}^{\left( i \right)}}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{B}}^{\left( i \right){\rm{T}}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\left( i \right)}}} \right)^{ - 1}} $

(21)

3 算例分析 3.1 算例1

利用MATLAB模拟数据，取球心坐标真值为a=20，b=30，c=40，球半径真值为r=5。在球面上选取12点，12个点的坐标真值如表 1所示。模拟时在12个点坐标上加入期望为0、中误差为0.1 m、服从正态分布的随机误差。为了比较分析，采用如下两种方案。

1) 加权总体最小二乘(WTLS)^[12]。系数矩阵的协因数阵和观测向量的协因数阵按下式计算：

$ {\mathit{\boldsymbol{Q}}_A} = \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{M}}^{\rm{T}}},{\mathit{\boldsymbol{Q}}_Y} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{Q}}_l}{\mathit{\boldsymbol{N}}^{\rm{T}}} $

(22)

式中，$\mathit{\boldsymbol{N}} = \left[{\begin{array}{*{20}{c}} {2{x_1}}&0& \cdots &0&{2{y_1}}&0& \cdots &0&{2{z_1}}&0& \cdots &0\\ 0&{2{x_2}}& \cdots &0&0&{2{y_1}}& \cdots &0&0&{2{z_2}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0& \vdots &{2{x_{12}}}&0&0& \vdots &{2{z_{12}}}&0&0& \vdots &{2{z_{12}}} \end{array}} \right], \mathit{\boldsymbol{M}} = \left[\begin{array}{l} \mathit{\boldsymbol{J}}\\ \mathit{\boldsymbol{K}} \end{array} \right]$，J =2I₃₆，K = 0 _12×36，I₃₆为36×36的单位矩阵，0_12×36为12×36的零矩阵。

2) 本文的总体最小二乘(ITLS)。模拟500次实验，将500次参数估值的平均值列于表 2。

从表 2可以看出，本文方法的计算结果参数估值的平均值与真值之差要小于WTLS计算的参数估值平均值与真值之差，计算结果更为接近真值，说明本文的方法更为可靠，能够得到更好的计算结果。

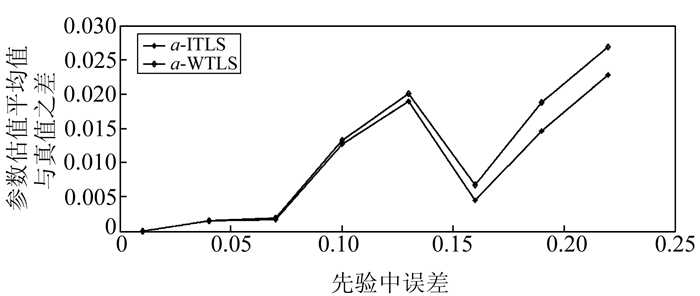
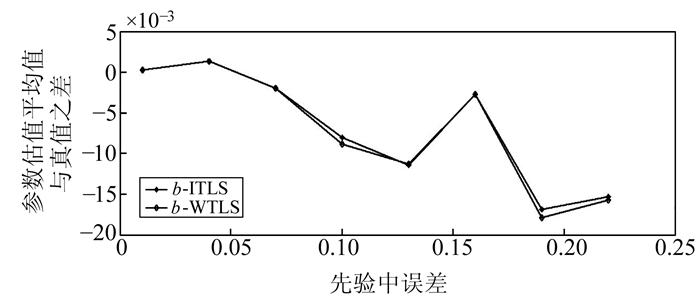
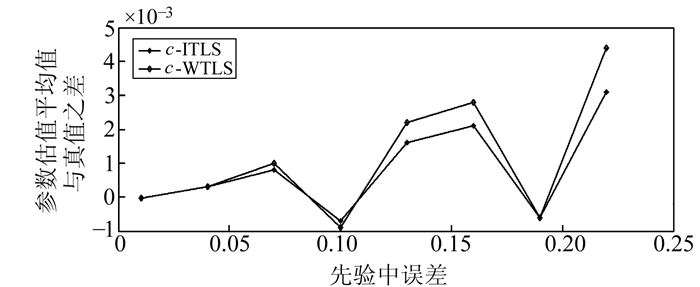
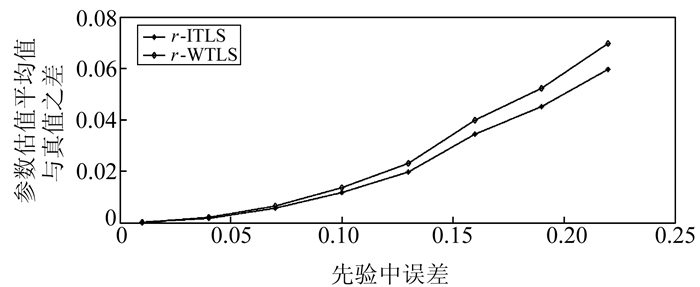
为了进一步说明本文方法的有效性，现进行如下实验。向坐标加入从0.01 m开始到0.22 m结束、步长为0.03的中误差，每个先验中误差下模拟500次，同样采用WTLS和ITLS进行计算。两种方法得到的参数估值的平均值与真值之差同先验中误差的关系如图 1~4所示。

从图中可以看出，在加入误差较小时，两种算法的计算结果差异不大，随着加入的误差越来越大，两种算法的计算结果偏离真值越远。整体看来，ITLS计算结果要优于WTLS的计算结果，每次计算结果都更为接近真值，特别是球半径的计算结果改进较为明显。因为WTLS没有考虑观测向量中的非线性形式，导致WTLS计算结果不合理，而ITLS则考虑了这一问题，可以得到更为可靠的参数估计。

3.2 算例2

采用表 1中相同的真值，对1~4号点的三维坐标加入中误差为0.1 m的随机误差，5~8号点的三维坐标加入中误差为0.2 m的随机误差，9~12号点的三维坐标加入中误差为0.3 m的随机误差，比较在精度不等的情况下两种算法的计算结果。同样模拟500次实验，计算参数估值的平均值，计算结果列于表 3。

从表 3可以看出，ITLS计算结果比WTLS要好，与真值更为接近，说明在精度不等的情况下ITLS同样有效，更加说明了本文方法的可行性。

4 结语

本文将总体最小二乘应用到球面拟合中，推导了一种改进的总体最小二乘算法。这种算法考虑到了观测向量中的非线性形式，还能保证系数矩阵和观测向量中不同位置的相同元素有相同的改正数，理论更为严谨。通过与加权总体最小二乘算法进行比较发现，本文方法的计算结果更为可靠，可以得到更准确的参数估值。