由于三维测量设备都具有一定的视场角,又要保证相邻测站之间具有一定的重合度,因此对于工程中尺寸巨大的物体就无法一次性进行测量,同时只能得到物体表面的数据信息。为得到整个被测物体表面的空间数据信息,就需要围绕目标物体进行多站扫描,从而造成在不同视角下测量坐标系的不同,因此将多测站数据转换到统一的坐标系下是必不可少的一步。点云配准的精度和效率直接影响点云三维建模的精度与效率[1]。1987年,Horn等[2]基于四元数法提出点集对点集的配准方法,成为解决复杂配准问题的关键方法。1992年,Besl等[3]介绍一种高层次的基于自由形态曲面的配准方法,也称为迭代最近点法ICP(iterative closest point),该方法首次利用点点距离进行约束。Chen等[4]利用点到最近点切平面的距离代替点点之间的欧氏距离进行迭代。在点云数据的采样方面,许多学者也进行了改进,Greg提出统一采样法,Blais等结合逆向标定法和随机搜寻法来提高速度,Masuda提出随机采样法,Rusinkiewicz提出最大化点法向量分布采样法[5-6]。2011年,Meng[7]提出基于采样球来寻找两组点云间相互对应的点。
ICP算法要求两个待匹配点集须有相当大的重叠区域,如果重叠度较低,则得不到好的配准结果。本文提出了一致性球的配准算法,可以克服ICP算法要求重叠度高的缺点。
1 一致性球的基本概念在目前的基于几何特征的点云配准算法中,常用三角形和4个共面点等几何模型来找寻对应点之间的相应关系。但是,这些都是二维描述子,只能得到少量的相互对应的点[8]。本文把三维球体作为特征描述子,且该描述子具有旋转不变的特性。
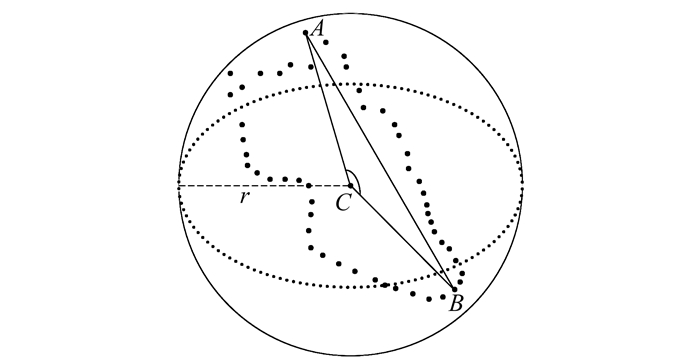
如图 1,用P表示点云数据集,数据集的每个点C都能够构成一个球体S,并把C和r当作球心与半径。与此同时,球体S的表面会包含数据集P中的一些点,将这些点所构成的集合记作D。用{C,D}表示上面所描述的球模型。
|
图 1 一致性球模型 Fig. 1 Consistent sphere model |
由上可知,对任一点都能构建一个球体,该球的球心即是该点,半径则为r。在要进行匹配的两组初始点云数据中,能够满足下列条件的任意两个球体{C,D}和{C′, D′}被认为是一致性球:
1) 两个球体具有相同的半径r;
2) 点集D中的点经过平移、旋转转换后可以与D′中的点相互对应匹配。
一致性球的球面上的对应点不能少于3组。如果由上述方法得到的两个球体是满足需要的球体,那么球体的球心C和C′便是一组对应点。
2 寻找对应点的算法上述算法的提出受益于Pilu等[9],该算法充分利用周围点的信息,对应点的准确度大大提高。本文将这种改进的基于SVD的配准方法由立体图像引入到3D点云数据。
已知两组待配准的初始点云数据集,球体模型分别为{C,J}和{C′, I},其中J={bj}(j=1, 2, …n),I={ai}(i=1, 2, …m),ai={xi, yi, zi}, bj={xj, yj, zj},则对应点寻找的流程如下。
1) 构建m×n矩阵G,且任一元素满足[9]:
| $ {G_{ij}} = [{e^{\frac{{-{{({C_{ij}}-1)}^2}}}{2}}}] \cdot {{\rm{e}}^{\frac{{ -r_{ij}^2}}{{2{\sigma ^2}}}}} $ |
式中,Ai是I中任一点,并寻找该点的邻域;Bj是相应的点。
2) 对矩阵G作SVD分解,得G = UDV,其中U是m维正交矩阵,V是n维正交矩阵,D表示非负对角矩阵(D满足Dij=0(i≠j), Dij>0)。
3) 用1替代矩阵D中的对角线元素Dij,得到一个新的m×n矩阵E。令P= UEV得到新的正交矩阵P,其中P的行元素表示点集I中任意点,列元素表示点集J中任意点,元素pij表示点ai和bj之间的匹配程度。
4) 如果pij不仅是第i行中元素的最大值,还是第j列中元素的最大值,那么可以把I点集中的第i个元素和J点集中的第j个元素当作一组相对应的点。
3 提取一致性球的方法已知初始数据集P中以r为半径的球{C,D},要在点云Q中找到一个大致相同的一致性球{C′, D′}。由于仪器设备和外部原因,采集到的点云中会含有噪声,因此近似球的半径并不严格为r。所以,为Q中的每一点构建一个半径区间为{r-δ, r+δ}的球体,也即是在数据集D′中,球心C′与每个数据点的距离属于区间{r-δ, r+δ}。接着,便需要在数据集Q中构造的所有球体中找到球{C,D}的一致性球{C′, D′}。
当球体半径相同时,点集D与D′中匹配点的个数是判断两个球体能不能成为一致性球的核心。因此,对应点非常重要。一致性球提取的具体流程如下。
1) 遍历{C,D}数据集D中的所有点,找出欧氏距离最大的两个点am1和am2,并保证am1、am2、C 3个点不在一条直线上。将该距离记为a-max,其中am1、am2∈(a)i。
2) 同样,在{C′, D′}数据集D′中寻找距离最大的两个点bm1和bm2,并将距离记为b-max。
3) 计算|a-max-b-max|的值,若该值超过限定值,则认为球{C′, D′}不正确,否则进入下一步。
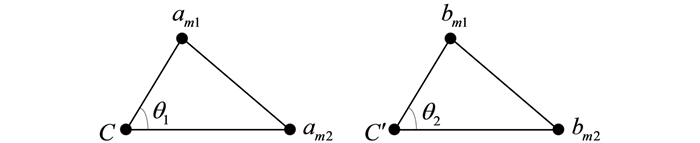
4) 此时得到两组对应关系:{(am1, bm1), (am2, bm2), (C, C′)}和{(am1, bm2), (am2, bm1), (C, C′)},如图 2所示。设定相应的距离阈值与角度阈值dth、θth满足条件‖amiC-bmjC′‖≤dth且‖θ1-θ2‖≤θth,则认为这是正确的对应点[10],将此对应点保留。
|
图 2 对应匹配点对示意图 Fig. 2 Corresponding points matching on sketch |
5) 根据步骤4)计算出旋转平移矩阵,记为R、T,并对数据集D进行更新。更新后的点集记为D1,使用前文提出的寻找对应点的算法寻找{D1, D′}的对应点。
6) 若对应点数量达到限值,就认为两个球体是一致性球,否则继续下个球的寻找。
4 基于扩散一致性球的精细配准考虑全局收敛性问题,如果只有局部的一个或几个一致性球,那么获得的空间匹配点也是很少的,未必能够做到算法的全局收敛性。所以需要考虑:1)找到的一致性球不一定和给定的球完全保持对应;2)仅用一组或几组对应球得到的对应点进行配准,得到的只是局部结果,不能代表全局;3)点集中含有噪声点的影响。由此可以看出,仅用一组或几组对应球得到的对应点求得的R和T具有局限性,精度不高。为了解决这些问题,需要对一致性球进行扩散。
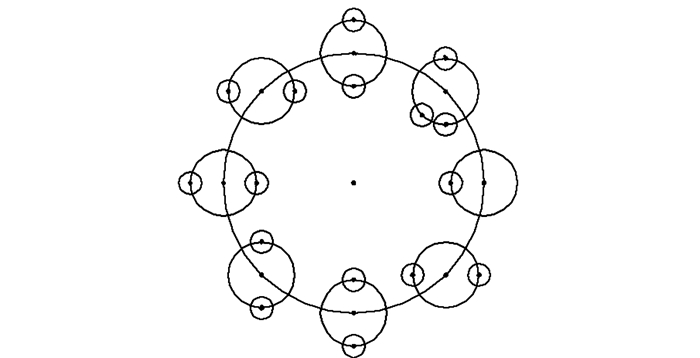
4.1 一致性球的扩散图 3为初始点云数据集构建一致性球后进行扩散的示意图,点云中的点用黑点表示。扩散的具体流程如下。
|
图 3 一致性球的扩散 Fig. 3 Spread of the consistent goal |
1) 把已得到的一组一致性球当作第一层,然后以该层为基础进行扩散;
2) 从首层一致性球表面上的对应点进行扩散,把每一组的对应点作为球心、r为半径作球;
3) 对得到的一致性球进行判断,验证其正确性,并且获得较多的对应点。
4.2 刚性约束剔除错误点对在对应点对搜索过程中难免会出现错误配准现象,有效地添加相应的约束条件来剔除这些误配准点,能提高算法的精度与鲁棒性。
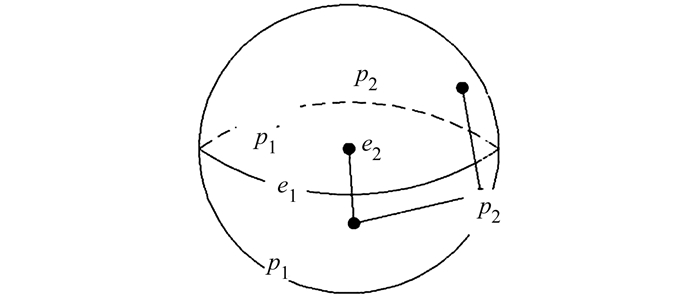
假设配准点对为(p1,p′1)和(p2, p′2),得到刚性约束理论(如图 4):
|
图 4 刚性约束 Fig. 4 Sketch of rigid constraint |
| $ \parallel p{\prime _2}-p{\prime _1}\parallel \le 2({e_1} + \parallel {p_2}-{p_1}\parallel ) $ | (1) |
证明:假设
| $ \parallel p{\prime _2}-p{\prime _1}\parallel > 2({e_1} + \parallel {p_2}-{p_1}\parallel $ | (2) |
根据三角不等式原理得到:
| $ \begin{array}{l} \parallel p{\prime _2}-p{\prime _1}\parallel = \parallel p{\prime _2}-{p_1}-p{\prime _1} + {p_1}\parallel \le \\ \parallel p{\prime _2} - {p_1}\parallel + \parallel p{\prime _1} - {p_1}\parallel = \\ \parallel p{\prime _2} - {p_2} + {p_2} - {p_1}\parallel + {e_1} \le \\ \parallel p{\prime _2} - {p_2}\parallel + \parallel {p_2} - {p_1}\parallel + {e_1} \end{array} $ | (3) |
而且
| $ \begin{array}{l} {e_1} + \parallel {p_2}-{p_1}\parallel = \parallel p{\prime _1}-{p_1}\parallel + {\rm{ }}\\ \parallel {p_1}-{p_2}\parallel \ge \parallel p{\prime _1} - {p_2}\parallel \end{array} $ | (4) |
结合式(1)~(4)可以得到‖p′2-p2‖>‖p′1-p2‖,与配准原理相悖。因此假设不成立,理论得证。
这个理论指出,对于随意给出的一个点对(p1, p′1),对于P中任意一点寻找其在P′中对应点p′2时,应满足如下条件:p′2应该落在以p′1为球心、半径为2(‖p2-p1‖+e1)的球形内部。这个理论十分重要,因为它将搜索范围从原来的P′缩小到一个由‖p2-p1‖以及初次点对配准误差e1确定的球形内部,而且适用于任何形状的点云数据。
只要初始配准位置不是十分差,总能找到这样的满足误差e1在限界内的点对(p1, p′1)。定义一个相关误差RIDD(relative intrapoint distance difference)并给出相关误差的限界:
| $ \begin{array}{l} -1 \le {\rm{ }}\frac{{\parallel p{\prime _2}-p{\prime _1}\parallel-\parallel {p_2} - {p_1}\parallel }}{{\parallel {p_2} - {p_1}\parallel }} \le \\ \frac{{2{e_1}}}{{\parallel {p_2} - {p_1}\parallel }} + 1 \end{array} $ | (5) |
根据相关误差得到结论:点对(p1, p′1)配准的误差越小,p1、p2两点相距越远,就越能把相关误差控制在一个更小的范围内,这表示在配准点出现违反刚性约束的条件时能被检测。这种理论对于一些特征提取配准方法[7-10]具有很强的吸引力,因为它们无法判别所寻找的点对是否满足了刚性约束。
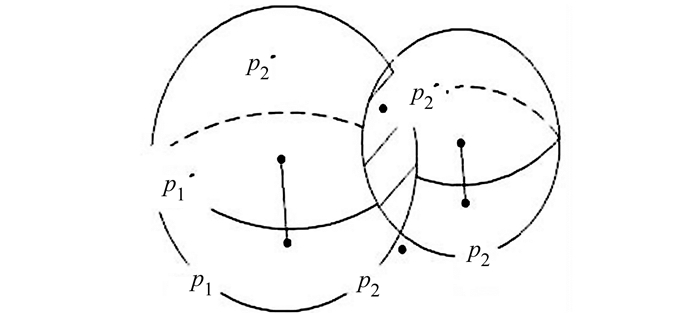
接着拓展到3组点对。假设已经存在的两组点对为(p1, p′1)和(p2, p′2),现在在参考点云P中任意找一点p3,那么其在目标点集P′中的对应点p′3应该落在这样的区域里:在两个球体的相交部分,这两个球体分别以p′1和p′2为球心,半径分别为2(‖p′1-p1‖+‖p3-p1‖)和2(‖p′2-p2‖+‖p3-p2‖)(图 5)。
|
图 5 3组点对刚性约束 Fig. 5 Three sets of points on the rigid constraints |
为了验证理论的合理性,给出两个球体必然相交的证明。根据三角不等式原理以及误差的非负性质,可以得出以下不等式推导:
| $ \begin{array}{l} \parallel p{\prime _2}-p{\prime _1}\parallel \le 2({e_1} + \parallel {p_2}-{p_1}\parallel ) \le 2({e_1} + {\rm{ }}\\ \parallel p{\prime _2}-{p_2}\parallel + \parallel {p_3} - {p_2}\parallel + \parallel {p_3} - {p_1}\parallel ) \end{array} $ | (6) |
即D < r+R,理论得证。这种约束同样不仅剔除了错误配准点,还能提高搜索速度。
同样,要拓展到k组点对的情况如下。假设k组匹配点对,得到以下一系列约束条件:
| $ \begin{array}{l} \parallel p{\prime _l}- p{\prime _j}\parallel \le {\rm{mi}}{{\rm{n}}_{i, i \ne l}}(\parallel p{\prime _i}- {p_i}\parallel + \\ \parallel {\rm{ }}{p_l}- {p_i}\parallel ) + \parallel {p_l} - {p_j}\parallel + \parallel p{\prime _j} - {p_j}\parallel \\ \left( {j, l \in [2, k]} \right) \end{array} $ | (7) |
对于k组点对,存在着多种组合方式进行约束,提供了足够的约束条件来得到精确的配准点对。对得到的精确点对使用四元数法求解R和T,完成配准。
4.3 实例验证为验证本文提出的方法,对来自斯坦福大学数据库的斯坦福兔数据和公鸡模型数据进行配准实验。图 6分别为0°、45°和90°的原始点云数据,分别对0°和45°、45°和90°、0°和90°的点云进行配准实验,结果如图 7~9所示。

|
图 6 Bunny原始数据 Fig. 6 Bunny the raw data |
|
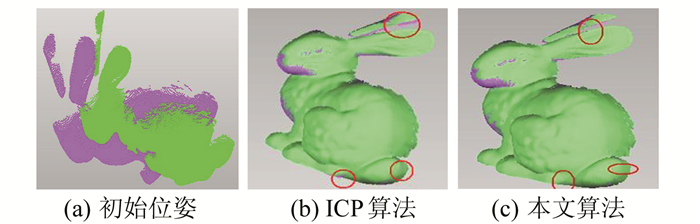
图 7 0°和45°点云配准结果 Fig. 7 Point cloud registration results of 0°and 45° |

|
图 8 45°和90°点云配准结果 Fig. 8 Point cloud registration results of 45°and 90° |

|
图 9 0°和90°点云配准结果 Fig. 9 Point cloud registration results of 0°and 90° |
图 7是0°点云和45°点云的配准结果,由(b)和(c)中红色圈的范围可知,本文算法在配准精度上优于传统的ICP算法。
图 8和图 9分别是45°点云和90°点云、0°点云和90°点云的配准结果。很明显,由于配准前两组点云的重叠度较低,所以单独使用ICP配准算法根本无法得到正确的匹配结果。而本文提出的算法可以克服这种局限,并能够得到较好的配准结果(配准精度在0.5 mm以内)。
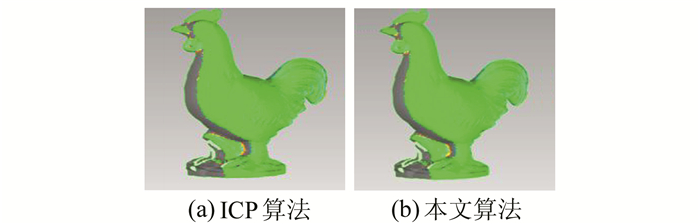
对公鸡模型的4站数据进行配准实验。图 10(a)是公鸡模型第1站和第2站点云的初始位姿,二者的重叠区域较大。图 10(b)和(c)是使用ICP算法和本文算法得到的配准结果,二者的配准效果都较好。为了直观地观察配准效果,对其进行精度分析,如图 11所示。ICP算法和本文算法大部分的配准精度都在0.2 mm以下,但ICP算法却有一小部分配准精度达到2 mm,本文算法所有的配准精度不超过0.6 mm。所以,当重叠区域较大时,ICP算法和本文算法都能达到较好的配准结果,但整体来讲,本文算法精度要高于ICP算法。

|
图 10 1站和2站点云配准结果 Fig. 10 Point cloud registration results of stations 1 and 2 |
|
图 11 配准结果精度分析 Fig. 11 Accuracy of registration results |
图 12(a)、13(a)分别为公鸡模型第1站和第3站、第1站和第4站点云的初始位姿,都只有部分重叠区域。配准结果分别如图 12(b)、12(c)和13(b)、13(c)所示。由图 12的点云融合度以及图 13鸡冠、前身和底座可知,ICP算法不能完成较好的配准结果,精度远小于本文算法。

|
图 12 1站和3站点云配准结果 Fig. 12 Point cloud registration results of stations 1 and 3 |

|
图 13 1站和4站点云配准结果 Fig. 13 Point cloud registration results of stations 1 and 4 |
针对三维建模中经典ICP算法在点云重叠度低时配准精度不高的问题,本文提出一种基于一致性球的配准算法。该算法在寻找对应点方面,创新性地将球体的旋转不变性与基于邻域的SVD正交一致性算法结合起来,找寻点云中在相应的一致性球上的对应点,克服了传统ICP算法要求点云重叠度高的问题。实验显示,当模型的重叠度较高时,本文算法和传统ICP算法都能得到较好的配准结果,但本文算法的精度优于传统ICP算法;当重叠度较低时,单纯使用传统ICP算法得不到正确的配准结果,而本文算法可以得到较好的配准结果。
| [1] |
周春艳, 李勇, 邹峥嵘. 三维点云ICP算法改进研究[J]. 计算机技术与发展, 2011, 21(8): 75-77 (Zhou Chunyan, Li Yong, Zou Zhengrong. Three - Dimensional Cloud ICP Algorithm Improvement[J]. Computer Technology and Development, 2011, 21(8): 75-77)
(  0) 0) |
| [2] |
Horn B K P. Closed-Form Solution of Absolute Orientation using Unit Quaternions[J]. Journal of the Optical Society of America, 1987, A(4): 629-642
(  0) 0) |
| [3] |
Besl P J, McKay N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256 DOI:10.1109/34.121791
(  0) 0) |
| [4] |
Chen Y, Medioni G. Object Modeling by Registration of Multiple Range Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991(3): 24-27
(  0) 0) |
| [5] |
Blais G, Levine M. Registering Multi View Range Data to Create 3D Computer Objects[J]. IEEE Transactions on Industry Applications, 1995, 17(8): 1128-1130
(  0) 0) |
| [6] |
Rusinkiewicz S, Levoy M. Efficient Variants of the ICP Algorithm[J]. IEEE Transactions on Industry Applications, 2001(2): 145-152
(  0) 0) |
| [7] |
Meng Y, Gu D, Zhang F, et al. Ordered Mesoporous Polymers and Homologous Carbon Frameworks: Amphiphilic Surfactant Templating and Direct Transformation[J]. Angewandte Chemie, 2011, 117(43): 7215-7221
(  0) 0) |
| [8] |
肖慧敏. 点云数据的配准算法[D]. 西安: 西安电子科技大学, 2013 (Xiao Huimin. A New Registration Method of Point Cloud Data[D]. Xi'an: Xidian University, 2013)
(  0) 0) |
| [9] |
Pilu M. A Direct Method for Stereo Correspondence Based on Singular Value Decomposition[C]. Computer Society Conference on IEEE, 1997
(  0) 0) |
| [10] |
严剑锋, 邓喀中. 基于特征点提取和匹配的点云配准算法[J]. 测绘通报, 2013(9): 62-65 (Yan Jianfeng, Deng Kazhong. Point Cloud Registration Algorithm Based on Extracting and Matching Feature Points[J]. Bulletin of Surveying and Mapping, 2013(9): 62-65)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

