2. 桂林市测绘研究院,广西壮族自治区桂林市临桂路12号, 541002;
3. 广西壮族自治区地理信息测绘院, 广西壮族自治区柳州市东环大道10号, 545006
目前建筑物沉降预测的统计研究逐渐受到重视,运用统计方法对变形数据的处理也越来越多样化,如时序分析模型[1-2]、半参数模型[3]、回归模型[4]和灰色模型[5-6]等各种统计模型已应用于建筑变形数据分析。对于同一组数据,采用不同的单项预测方法得出的预测结果不尽相同,因此如果选择的预测方法不当,就有可能导致预测不准确。综合利用各种预测模型的信息,以适当的加权平均形式得出组合预测模型,被很多学者应用到建筑变形数据处理中。陈华友等[7]指出,传统的组合预测方法是按照单项预测方法的不同而赋予不同的加权平均系数,同一个单项预测方法在样本区间上各个时点的加权平均系数是不变的,但实际上,就同一个单项预测方法而言,它在不同时刻的表现可能不相同,即在某个时点上的精度较高,而在另一时点上的预测精度较低。诱导有序加权平均算子(IOWA)通过每个单项预测方法在样本区间上各个时点的拟合精度的高低按顺序赋权,该种赋权思想解决了传统组合预测模型赋权的缺陷。本文结合IOWA算子与Theil不等系数最小化准则,提出一种基于Theil不等系数的IOWA算子最优变形组合预测模型,并将其应用于建筑物变形监测分析与预测中,最后通过工程实例验证本文方法的可行性与精度。
1 模型建立假设预测对象某个指标的时间序列观测值为{xt, t=1, 2, …, N},有m种可行的单项预测方法对其进行预测,xit为第i种(i=1, 2, …, m)预测方法在t时刻的预测值,则有
令
| $ \begin{array}{*{20}{c}} {{a_{it}} = \left\{ \begin{array}{l} 1 - \left| {{e_{it}}} \right|,当\left| {{e_{it}}} \right| \le 1\\ 0,当\left| {{e_{it}}} \right| > 1 \end{array} \right.}\\ {i = 1,2, \cdots ,m;t = 1,2, \cdots ,N} \end{array} $ | (1) |
式中,eit=(xt-xit)/xt为第i种预测方法在t时刻的预测相对误差,则ait表示第i种预测方法在t时刻的预测精度,且ait∈[0, 1]。将预测精度ait看成预测值xit的诱导值,则m种单项预测方法在t时刻的预测精度和其对应的样本区间的预测值就构成了m个二维数组(〈a1t, x1t〉, 〈a2t, x2t〉, …, 〈amt, xmt〉)。将m种单项预测方法在t时刻的预测精度序列a1t、a2t、…amt按从大到小的顺序排列,设a-index(it)是第i个预测精度的下标,根据诱导有序加权平均的概念,可以定义IOWA算子的组合预测值如下:
| $ \begin{array}{*{20}{c}} {\hat x = {\rm{IOW}}{{\rm{A}}_p}\left( {\left\langle {{a_{1t}},{x_{1t}}} \right\rangle ,\left\langle {{a_{2t}},{x_{2t}}} \right\rangle , \cdots ,\left\langle {{a_{mt}},{x_{mt}}} \right\rangle } \right) = }\\ {\sum\limits_{i = 1}^m {{p_i}{x_{a - {\rm{index}}\left( {it} \right)}}} } \end{array} $ | (2) |
式中,
| $ \begin{array}{*{20}{c}} {{{\hat e}_t} = {x_t} - {{\hat x}_t} = {x_t} - }\\ {\sum\limits_{i = 1}^m {{p_i}{x_{a - {\rm{index}}\left( {it} \right)}}} = \sum\limits_{i = 1}^m {{p_i}{e_{a - {\rm{index}}\left( {it} \right)}}} } \end{array} $ | (3) |
由文献[8]可得:
| $ \left\{ \begin{array}{l} {\tau _i} = \sqrt {\sum\limits_{t = 1}^N {{{\left( {{x_t} - {x_{it}}} \right)}^2}} } /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } ,i = 1,2, \cdots ,m\\ \tau = \sqrt {\sum\limits_{t = 1}^N {{{\left( {{x_t} - {{\hat x}_t}} \right)}^2}} } /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } \end{array} \right. $ | (4) |
式中,τi为第i种预测方法预测值与实际值序列改进的Theil不等系数(τi∈[0, ∞)),τ为IOWA组合预测值序列与实际值序列的改进Theil不等系数(τ∈[0, ∞))。τ值越小表示组合预测精度越高,当τ=0时,
| $ \begin{array}{*{20}{c}} {\sum\limits_{t = 1}^N {{{\left( {{x_t} - {{\hat x}_t}} \right)}^2}} = \sum\limits_{t = 1}^N {{{\left( {{{\hat e}_t}} \right)}^2}} = }\\ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{p_i}{p_j}\left( {\sum\limits_{t = 1}^N {{e_{a - {\rm{index}}\left( {it} \right)}}{e_{a - {\rm{index}}\left( {it} \right)}}} } \right)} } } \end{array} $ | (5) |
故Theil不等系数又可表示为:
| $ \left\{ \begin{array}{l} {\tau _i} = \sqrt {\sum\limits_{t = 1}^N {{{\left( {{e_{it}}} \right)}^2}} } /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } ,i = 1,2, \cdots ,m\\ \tau = \sqrt {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{p_i}{p_j}\left( {\sum\limits_{t = 1}^N {{e_{a - {\rm{index}}\left( {it} \right)}}{e_{a - {\rm{index}}\left( {it} \right)}}} } \right)} } } /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } \end{array} \right. $ | (6) |
记P =(p1, p2, …, pm)T,则P表示组合预测加权系数列向量。令
| $ {e_{ij}} = \sum\limits_{t = 1}^N {{e_{a - {\rm{index}}\left( {it} \right)}}{e_{a - {\rm{index}}\left( {jt} \right)}}} ,i,j = 1,2, \cdots ,m $ | (7) |
则称E =(eij)(m×m)为m阶IOWA算子的组合预测误差信息方阵,则式(5)的结果可以写成:
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{p_i}{p_j}\left( {\sum\limits_{t = 1}^N {{e_{a - {\rm{index}}\left( {it} \right)}}{e_{a - {\rm{index}}\left( {it} \right)}}} } \right)} } = }\\ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{p_i}{p_j}{e_{ij}}} } = {\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{EP}}} \end{array} $ | (8) |
由式(6)、(8)知,IOWA算子的组合预测值序列与实际值序列的Theil不等系数τ可表示为:
| $ \tau = \sqrt {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{EP}}} /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } $ | (9) |
由式(9)可知,基于Theil不等系数的IOWA算子组合预测值序列与实际值序列的Theil不等系数为组合预测方法的加权系数p1, p2, …pm的函数,记为τ(p1, p2, …pm)。当τ(p1, p2, …pm)越小,表示组合预测方法越有效,则基于Theil不等系数的IOWA算子组合预测模型可表示成如下最优模型:
| $ \begin{array}{*{20}{c}} {\min \tau \left( {{p_1},{p_2}, \cdots ,{p_m}} \right) = \sqrt {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{EP}}} /\sqrt {\sum\limits_{t = 1}^N {x_t^2} } }\\ {{\rm{s}}.\;{\rm{t}}.\left\{ \begin{array}{l} \sum\limits_{i = 1}^m {{p_i} = 1} \\ {p_i} \ge 0,i = 1,2, \cdots ,m \end{array} \right.} \end{array} $ | (10) |
根据预测的原则,可用上述过程求出的IOWA算子组合预测的最优权系数P*=(p1*, p2*, …, pm*)T进行预测。假设预测区间为[N+1, N+2, …],则IOWA预测公式可表示为:
| $ \begin{array}{*{20}{c}} {{\rm{IOW}}{{\rm{A}}_p}\left( {\left\langle {{a_{1t}},{x_{1t}}} \right\rangle ,\left\langle {{a_{2t}},{x_{2t}}} \right\rangle , \cdots ,\left\langle {{a_{mt}},{x_{mt}}} \right\rangle } \right) = }\\ {\sum\limits_{i = 1}^m {p_i^ * {x_{a - {\rm{index}}\left( {it} \right)}}} ,t = N + 1,N + 2, \cdots } \end{array} $ | (11) |
其中, 在预测区间[N+1, N+2, …]上预测精度序列a1t, a2t, …amt的大小确定原则是依据各种单项预测方法在区间上近几期拟合平均精度的高低,即若要进行未来k期的预测,则用第i种预测方法最近k期拟合精度
在实际工程建筑物的沉降变形监测中,时间间隔往往并不是那么规则,而是呈现出非等间隔的状态。这时需要把非等间隔的数列转化为等间隔序列,再进行预测模型的建立。本文采用拉格朗日线性插值进行非等间隔数据处理。为了评判本文预测模型的有效性与精度,采用平方和误差(SSE)、均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方百分比误差(MSPE)作为评价指标。
利用本文模型对湖南益阳某小区高层建筑物的沉降变形监测数据进行变形分析与预测,同时与G曲线模型、二次多项式模型以及传统组合模型进行对比分析。施工期间在建筑物的主要承重梁上共布设了12个沉降形变监测点,分别在不同时间间隔下进行沉降观测。本文选取其中1个监测点的沉降监测数据进行变形监测分析与预测,该监测点共观测20期,取前12期作为拟合建模区,后8期作为预测区。表 1列出该点后8期的原始观测数据。
|
|
表 1 监测点的原始沉降量 Tab. 1 The original settlement of the monitoring point |
1) 数据预处理。由于原始观测数据是非等时间间隔,故在进行建模分析之前,先采用上文所述的拉格朗日线性插值法对原始观测数据进行预处理,将非等时间间隔的数据转化成等时间间隔,以便进行预测模型的建立。后8期数据预处理结果如表 2所示。
|
|
表 2 预处理后监测点的沉降量 Tab. 2 The settlement of the monitoring point after preprocessing |
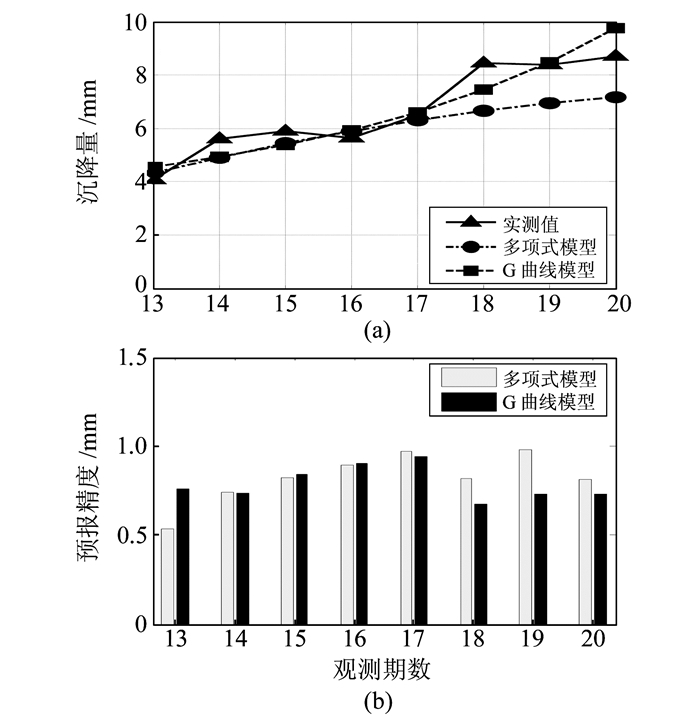
2) 单项预测模型的建立。本文选取G曲线模型与二次多项式模型对沉降监测数据进行建模分析与预测,2种单项模型的预测曲线与预测精度曲线如图 1所示。
|
图 1 单项模型预测值与预测精度对比 Fig. 1 Comparison of the individual models' predicted value and prediction precision |
由图 1可以看出,2个单项模型均可以较好地预测沉降形变的发展趋势,但随着时间的推移,多项式模型的预测精度逐渐偏低。综合对比分析图 1(a)与1(b)可知,G曲线模型的预测精度高于多项式模型。
3) 本文模型的建立。基于上述单项模型以及各单项模型的预测精度,建立基于Theil不等系数的IOWA算子最优变形组合预测模型。为与本文所提的基于Theil不等系数的IOWA算子最优变形组合预测模型进行对比,同时建立基于误差平方和最小的传统组合预测模型。2种组合模型的预测结果如表 3所示。
|
|
表 3 组合模型预测值对比 Tab. 3 Comparison of the combination models' predicted value |
由表 3可以得出,传统组合模型与本文方法的最大残差分别为-1.179 mm与-1.157 mm,本文方法的均方根误差为0.599 mm,传统组合模型的均方根误差为0.643 mm。综上所述,本文方法在一定程度改善了传统组合模型的预测精度。
4) 模型精度检验与对比分析。依据上述5种精度评价指标,对G曲线模型、二次多项式模型、传统组合模型以及本文模型进行精度评定,各种模型的精度评价指标的计算结果如表 4所示。
|
|
表 4 各种模型预测效果评价指标 Tab. 4 The evaluation indexs of the model forecast effect |
由表 4可知,2种组合模型的各项误差指标均低于G曲线模型与多项式模型,说明组合模型综合了单项模型的优势,提高了单项模型的预测精度。本文所建立的基于Theil不等系数的IOWA算子最优变形组合预测模型的各项误差指标相对于其他3种模型均较低,这进一步证明了本文方法较单项模型的优势以及本文方法在一定程度上优化了传统组合模型,提高了组合模型的预测精度。
4 结语1) 在沉降变形监测分析与预测中,基于Theil不等系数的IOWA算子最优变形组合预测模型,通过诱导有序加权平均IOWA算子,考虑不同时点上单项预测方法预测精度大小之间的改变,有效改善了模型的自适应性,在一定程度上优化了传统组合模型,提高了模型的预测精度。
2) 组合模型是建立在单一预测模型基础上的,因此在实际应用中,除了尽量选取不同角度的单项预测模型外,还要选取预测精度较高的单项预测模型,以提高组合预测模型的精度。
| [1] |
臧妻斌, 黄腾. 时间序列分析在地铁变形监测中的应用[J]. 测绘科学, 2014, 39(7): 155-157 (Zang Qibin, Huang Teng. Application of Time Series Analysis in Subway Deformation Monitoring[J]. Science of Surveying and Mapping, 2014, 39(7): 155-157)
(  0) 0) |
| [2] |
文富勇. 基于时间序列的地下水封洞库变形监测模型研究[J]. 人民长江, 2015, 46(24): 88-93 (Wen Fuyong. Research on Monitoring Model of Deformation of Underground Water-Sealed Cavern Based on Time Series Theory[J]. Yangtze River, 2015, 46(24): 88-93)
(  0) 0) |
| [3] |
许昌, 岳东杰, 董育烦, 等. 基于主成分和半参数的大坝变形监测回归模型[J]. 岩土力学, 2011, 32(12): 3738-3742 (Xu Chang, Yue Dongjie, Dong Yufan, et al. Regression Model for Dam Deformation Based on Principal Component and Semi-Parametric Analysis[J]. Rock and Soil Mechanics, 2011, 32(12): 3738-3742 DOI:10.3969/j.issn.1000-7598.2011.12.033)
(  0) 0) |
| [4] |
邓兴升, 陈石桥, 殷自成. 动态回归模型在变形分析中的应用[J]. 大地测量与地球动力学, 2011, 31(5): 132-135 (Deng Xingsheng, Chen Shiqiao, Yin Zicheng. Application of Dynamic Regression Model in Deformation Analysis[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 132-135)
(  0) 0) |
| [5] |
周吕, 文鸿雁, 韩亚坤. 灰色预测与Kalman滤波在建筑物沉降变形分析中的应用[J]. 测绘科学, 2014, 39(4): 149-152 (Zhou Lü, Wen Hongyan, Han Yakun. Application of Grey Prediction and Kalman Filter in Building Settlement Deformation Analysis[J]. Science of Surveying and Mapping, 2014, 39(4): 149-152)
(  0) 0) |
| [6] |
陶鑫, 文鸿雁, 何美琳, 等. 灰色二阶预测模型在变形监测中的应用[J]. 测绘科学, 2014, 39(6): 135-137 (Tao Xin, Wen Hongyan, He Meilin, et al. Application of Grey Prediction Model of Second Order in Deformation Monitoring[J]. Science of Surveying and Mapping, 2014, 39(6): 135-137)
(  0) 0) |
| [7] |
陈华友, 刘春林. 基于IOWA算子的组合预测方法[J]. 预测, 2003, 22(6): 61-65 (Chen Huayou, Liu Chunlin. A Kind of Combination Forecasting Method Based on Induced Ordered Weighted Averaging(IOWA) Operators[J]. Forecasting, 2003, 22(6): 61-65)
(  0) 0) |
| [8] |
陈华友. 组合预测方法有效性理论及其应用[M]. 北京: 科学出版社, 2008 (Chen Huayou. Combination Forecast Method and Its Application[M]. Beijing: Science Press, 2008)
(  0) 0) |
2. Guilin Institute of Surveying and Mapping, 12 Lingui Road, Guilin 541002, China;
3. The Second Institute of Surveying and Mapping of Guangxi, 10 East-Ring Road, Liuzhou 545006, China
 2018, Vol. 38
2018, Vol. 38

