2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 中国科学院大学,北京市玉泉路19号甲,100049
共模误差是影响GPS时间序列速度及其不确定度估值的主要因素。Wdowinski等[1]在分析1992年兰德斯地震形变场时首次发现共模误差(CME), 并提出使用堆栈滤波方法进行剔除。Nikolaidis[2]在Wdowinski基础上提出加权堆栈滤波方法。Dong等[3]采用PCA与KLE相结合的滤波方法进行CME剔除。田云锋[4-5]用相关加权滤波法对时间序列进行滤波。此外,学者们在此基础上对GPS时间序列进行应用研究[6-9],并进一步对各种方法进行了分析对比[10-11]。但相关文献中对大区域、长基线GPS网剔除共模误差的研究较少。本文分别采用叠加滤波、PCA、KLE方法提取欧洲区域平均基线长度2 000 km的12个IGS站点2006-01~2014-12共9 a的共模误差,并对3种方法的滤波效果进行对比分析。
1 共模误差的计算方法叠加滤波法是将单日解中误差作为权重,假定GPS网中所有测站的共模误差是相同的;PCA和KLE法都是基于数理统计分析而进行的正交变换,对不同测站分别剔除共模误差。
1.1 区域叠加滤波叠加滤波法[2]将单日解中误差作为权重。假设其在某空间内均匀分布,则:
| $ {\varepsilon _i} = \sum\limits_{S = 1}^{{S_i}} {\frac{{{v_{i, s}}}}{{\sigma _{i, s}^2}}/} \sum\limits_{S = 1}^{{S_i}} {\frac{1}{{\sigma _{i, s}^2}}} $ | (1) |
式中,εi为第i个台站的共模误差值;S为GPS站点数;v表示残余坐标时间序列;δi, s为单日坐标解中误差。
1.2 PCA/KLE方法PCA/KLE[3]都是正交分解方法,通过矩阵变换构造出尽可能不相关的新变量,从中提取有价值的信息以达到用少量新变量代替原始变量的目的。残差矩阵为X (i, j)(i=1, …, m, j=1, …, n),元素xi, j表示第j天第i个历元的坐标误差,m>n。X的协方差矩阵定义为:
| $ \boldsymbol{B} = \frac{1}{{m-1}}{\boldsymbol{X}^{\rm{T}}}\boldsymbol{X} $ | (2) |
利用协方差向量σ对协方差矩阵进行标准化,可得关联矩阵C。如cij=bij/(σiσj),σ定义为:
| $ {\sigma _j} = \sqrt {{b_{jj}}} = \sqrt {\frac{1}{{m-1}}\sum\limits_{k = 1}^m {{\boldsymbol{X}^2}(k, j)} } $ | (3) |
关联矩阵通过分解可以得到:
| $ \mathit{\boldsymbol{X = W}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_c}{\mathit{\boldsymbol{W}}^{\rm{T}}} $ | (4) |
PCA和KLE的不同之处在于PCA是使用协方差矩阵B进行变换,而KLE则采用关联矩阵C来计算正交矩阵。特征值的大小反映了相应分量对残差时间序列贡献率的大小,将特征值从大到小排列,将前几个模式分量之和称为主分量,它包含了原始数据的大部分信息。主分量可以由下式计算:
| $ {\varepsilon _{i, j}} = \sum\limits_{k = 1}^P {{a_{i, k}}{v_{j, k}}} $ | (5) |
式中,P为具有较大特征值的分量个数,通常把其中空间响应比较一致的分量称为共模误差。
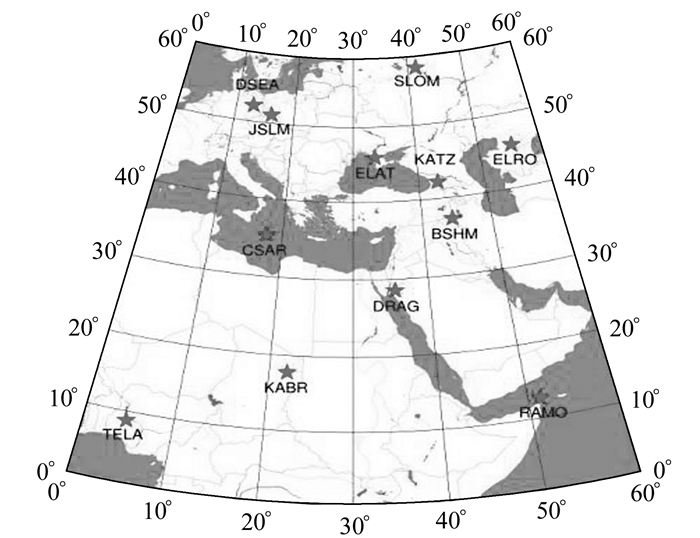
2 GPS时间序列处理本文采用SOPAC提供的GPS时间序列,从中选取欧洲12个IGS站点9 a的数据,站点之间平均基线长度为2 000 km。站点分布如图 1所示。
|
图 1 台站分布 Fig. 1 Distribution of IGS stations |
GPS台站时间序列中包含速度项、阶跃信号、周年和半周年项等非构造信号,GPS单站、单分量位置时间序列y(ti)通常满足:
| $ \begin{array}{l} y({t_i}) = a + b{t_i} + c{\rm{sin}}(2\pi {t_i}) + d{\rm{cos}}(2\pi {t_i}) + \\ e{\rm{sin}}(4\pi {t_i}) + f{\rm{cos}}(4\pi {t_i}) + \\ \sum\limits_{j = 1}^{{n_g}} {{g_j}H({t_i}-{T_{gj}})} + \sum\limits_{j = 1}^{{n_h}} {{h_j}H({t_i}-{T_{hj}}){t_i}} + \\ \sum\limits_{j = 1}^{{n_k}} {{k_j}} {\rm{exp}}(({t_i}-{T_{kj}})/{\tau _j})H({t_i} - {T_{kj}}) + {v_i} \end{array} $ | (6) |
其中,a表示初始位置,b表示速率,c、d、e和f分别表示年、半年周期项系数,g表示阶跃,h表示震后速率变化,k表示震后速率衰减指数模型,H表示阶梯函数,ti表示时间,v表示误差。
由于外界条件、硬件或软件原因,时间序列观测值中存在粗差,在进行时间序列分析时必须将这些粗差予以剔除。利用式(6)进行拟合,用实际数据y(ti)与拟合后对应数据u(ti)进行相减操作,得到新的时间序列del(ti)=y(ti)-u(ti)。计算del(ti)的标准差,式(7)为标准差计算公式:
| $ s = {(\frac{1}{{n-1}}\sum\limits_{i = 1}^n {{{({x_i}-\bar x)}^2}} )^{\frac{1}{2}}} $ | (7) |
剔除大于3倍中误差的数据。在进行时序分析时要求是等间隔的,因此需要对缺失或者是剔除后缺失的时间序列进行插值补齐。经过对比线性插值、多项式拟合和三次样条3种方法的插值效果,最终采用三次样条进行插值补齐,以使数据满足等间隔要求。
2.2 残差时间序列的获取利用式(6)对GPS站3个坐标分量的时间序列采用最小二乘方法,消除台站时间序列的阶跃项、速度项、对数衰减、指数等后,得到干净的残余坐标时间序列。
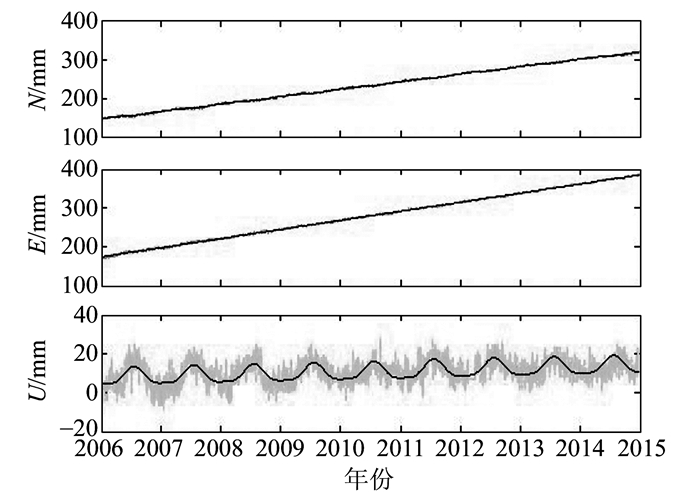
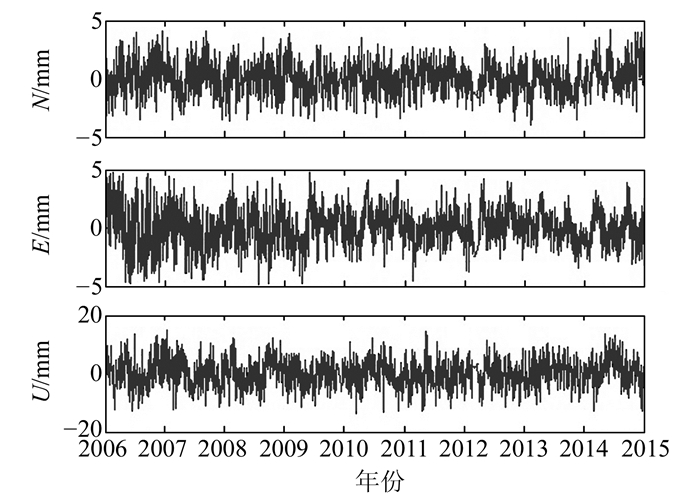
以RAMO站为例,图 2是原始时间序列,图 3是得到的残差时间序列。
|
图 2 原始时间序列(RAMO站) Fig. 2 Originaltime series (RAMO station) |
|
图 3 残差时间序列(RAMO站) Fig. 3 Residual time series (RAMO station) |
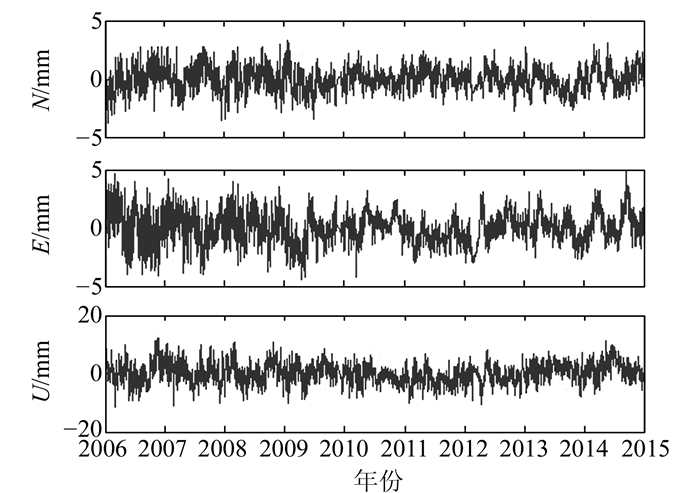
利用叠加滤波提取的共模误差如图 4所示。叠加滤波前后各站点均方根比较见表 1。
|
图 4 区域叠加滤波提取的共模误差 Fig. 4 Common mode error extracted by regional stacking |
|
|
表 1 叠加滤波前后各站点均方根比较 Tab. 1 Comparison between mean RMS before and after stacking filtering |
利用PCA、KLE法分别计算欧洲区域12个IGS站的前3个主成分的空间响应,分别对应三坐标分量。
采用PCA法得到的第一主成分贡献率分别为41.43%、50.21%、39.07%;第二主成分的贡献率分别为22.39%、17.53%、13.06%;第三主成分的贡献率为8.31%、6.84%、9.00%;第四主成分的贡献率为5.92%、4.57%、7.45%。前3个主成分累计贡献率为72.13%、74.58%、61.13%,前3个主成分的贡献率综合了大部分的有用信息,因此本文PCA采用这3个主成分的和作为区域共模误差。
采用KLE法得到的第一主成分的贡献率分别为44.76%、48.76%、40.4%;第二主成分的贡献率分别为17.94%、13.1%、9.78%;第三主成分的贡献率为8.01%、7.55%、7.92%;第四主成分的贡献率为5.45%、5.84%、6.64%。前3个主成分累计贡献率为70.71%、69.42%、58.1%,前3个主成分的贡献率综合了大部分的有用信息,因此本文KLE采用这3个主成分的和作为区域的共模误差。
表 2显示台站残差分别经过PCA、KLE两种滤波后的均方根,滤波前均方根参照表 1。

|
图 5 PCA法得到的空间响应 Fig. 5 Spatial response with PCA approach |

|
图 6 KLE法得到的空间响应 Fig. 6 Spatial response with KLE approach |
|
|
表 2 PCA/KLE滤波后各站点均方根 Tab. 2 Mean RMS after PCA/KLE |
为了进一步对比3种滤波方法的效果,对每一站滤波前后的均方根进行比较,得到各站3种方法滤波后均方根减少的百分比,如表 3所示。
|
|
表 3 滤波后各站均方根减少百分比 Tab. 3 Percent reduction of mean RMS after filtering |
基于本文选取的12个IGS台站,由表 3分析可以得出,整体而言,叠加滤波N、E、U 3个方向的平均剔除百分比分别为27.19%、27.62%、22.8%;PCA滤波后N、E、U 3个方向的平均剔除百分比分别为44.42%、43.61%、36.71%;KLE滤波后N、E、U 3个方向的平均剔除百分比分别为37.52%、35.72%、33.92%。进一步分析可得,N方向上PCA、KLE优于叠加滤波的站点数分别为9个和7个;E方向上PCA、KLE优于叠加滤波的站点数分别为12个和7个;U方向上PCA、KLE优于叠加滤波的站点数分别为9个和8个。部分台站空间特征明显,如KATZ站U方向、SLOM站N方向和E方向。总体而言,PCA、KLE两种滤波方法在大尺度空间域GPS网中,剔除共模误差的效果优于叠加滤波。
4 结语本文采用叠加滤波、PCA、KLE等3种方法对12个IGS站9 a的观测数据进行滤波,结果表明3种方法都能在一定程度上剔除区域GPS网中的共模误差。但叠加滤波假设所有站点的共模误差分布完全一致,具有局限性,对于小观测网比较适用,而对于较大的观测网,共模误差的分布可能不再均匀。本文特意选取平均基线长度2 000 km且个别台站(KATZ站、SLOM站)空间特征明显的较大区域GPS网来进行滤波分析,结果表明,PCA、KLE滤波效果明显优于叠加滤波。
| [1] |
Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 057-18 070 DOI:10.1029/97JB01378
(  0) 0) |
| [2] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [3] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen‐Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research Atmospheres, 2006, 111(B3)
(  0) 0) |
| [4] |
田云锋, 沈正康. GPS观测网络中共模分量的相关加权叠加滤波[J]. 地震学报, 2011, 33(2): 198-208 (Tian Yunfeng, Shen Zhengkang. Correlation Weighted Stacking Filtering of Common-Mode Component in GPS Obsvervation Network[J]. Acta Seismologica Sinica, 2011, 33(2): 198-208)
(  0) 0) |
| [5] |
田云锋. GPS位置时间序列中的中长期误差研究[D]. 北京: 中国地震局地质研究所, 2011 (Tian Yunfeng. Study on Intermediate-and Long-term Errors in GPS Position Time Series[D]. Beijing: Institute of Geology, CEA, 2011)
(  0) 0) |
| [6] |
Li W W, Shen Y Z, Li B F. Weighted Spatiotemporal Filtering Using Principal Component Analysis for Analyzing Regional GNSS Position Time Series[J]. Acta Geodaetica et Geophysica, 2015, 50(4): 1-18
(  0) 0) |
| [7] |
敖敏思, 胡友健, 赵斌, 等. PCA和KLE在高采样率GPS定位中的应用[J]. 大地测量与地球动力学, 2011, 31(6): 145-150 (Ao Minsi, Hu Youjian, Zhao Bin, et al. Application of PCA and KLE to high-rate positioning[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 145-150)
(  0) 0) |
| [8] |
殷海涛, 甘卫军, 熊永良, 等. PCA空间滤波在高频GPS定位中的应用研究[J]. 武汉大学学报:信息科学版, 2011, 36(7): 825-829 (Yin Haitao, Gan Weijun, Xiong Yongliang, et al. Study on the Effect of PCA Spatial Filtering on High-rate GPS Positioning[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 825-829)
(  0) 0) |
| [9] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1 372-1 384 (Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Characterisrics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1 372-1 384)
(  0) 0) |
| [10] |
胡守超, 伍吉仓, 孙亚峰. 区域GPS网三种时空滤波方法的比较[J]. 大地测量与地球动力学, 2009, 39(3): 95-99 (Hu Shouchao, Wu Jicang, Sun Yafeng. Comparison among Three Spatiotemporal Filtering Methods for Regional GPS Networks Analysis[J]. Journal of Geodesy and Geodynamics, 2009, 39(3): 95-99)
(  0) 0) |
| [11] |
贺小星, 花向红, 周世健, 等. PCA与KLE相结合的区域GPS网坐标序列分析[J]. 测绘科学, 2014, 39(7): 113-117 (He Xiaoxing, Hua Xianghong, Zhou Shijian, et al. Discussion on Geological Evaluation of Plateau Airport Engineering Using Remote Sensing and Geoscience Knowledge[J]. Science of Surveying and Mapping, 2014, 39(7): 113-117)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2018, Vol. 38
2018, Vol. 38


