2. 中国测绘科学研究院,北京市莲花池西路28号,100830;
3. 国家测绘地理信息局卫星测绘应用中心,北京市三虎桥北路百胜村1号院,100830
2016-05-30资源三号02星(ZY3-02)成功发射。其搭载三线阵测绘相机和多光谱相机等有效载荷,前后视相机分辨率优于2.7 m,并拥有更优异的影像融合能力、更高的图像高程测量精度。还搭载了双频GPS接收机,可以采用星载GPS观测数据实现精密定轨;同时装载了SLR激光反射器,可以采用SLR激光测距数据进行轨道精度外部检核。
利用星载GPS数据进行低轨卫星精密定轨是轨道确定的主要方法之一。随着星载GPS定轨技术在TOPEX/Poseidon卫星上的成功应用[1],国内外学者对CHAMP、SAC-C、Jason-1、GRACE等低轨卫星进行精密定轨,径向精度达到cm级。Svehla等[2]利用双差观测值对CHAMP卫星进行几何法和动力法定轨,精度均达到5 cm。美国喷气实验室[3-4]利用星载GPS数据对Jason-1卫星进行简化动力定轨,径向精度达到2 cm。Liu等[5]利用精密单点定位方法对CHAMP卫星定轨,位置精度为0.48 m。李建成等[6]利用非差运动学方法解算GRACE卫星精密轨道,径向精度为3~5 cm。赵春梅等[7-8]利用伪随机脉冲参数和简化动力学方法解算CHAMP卫星和资源三号卫星轨道,经过SLR数据检核,精度优于4 cm。因此,低轨卫星定轨已经达到cm级的定轨精度,并得到广泛应用。
本文基于激光联测需要,采用星载GPS数据和CODE快速星历,结合简化动力学方法实现了资源三号02星快速精密定轨,通过重叠弧段和SLR数据检核,快速精密定轨精度达到cm级,并根据定轨结果实现了短期m级轨道预报。
1 观测数据质量低轨卫星在太空中处于高速运动中,受复杂环境的影响,而星载GPS数据质量是卫星精密定轨的关键。影响观测数据质量的主要因素包括电离层延迟、多路径效应以及接收机噪声等。
GPS观测数据质量检核的主要指标为多路径效应(MP1、MP2)、周跳比(o/slps)和观测数据的完整性。其中,MP1、MP2分别为L1、L2频率上的多路径观测误差;周跳比直接反映了数据周跳情况,比值越大,周跳越少,反之则越多;数据的完整性反映了星载设备的性能和数据量大小,直接影响低轨卫星的定轨精度。
多路径效应误差可通过伪距观测值和载波相位观测值的线性组合来估计[9]:
| $ \begin{array}{l} M{P_1} = {P_1}- [1 + 2/\left( {\alpha-1} \right)]{\varphi _1} + [2/\left( {\alpha-1} \right)]{\varphi _2}\\ M{P_2} = {P_2} - [1 + 2/\left( {\alpha-1} \right)]{\varphi _1} + [2/\left( {\alpha-1} \right)]{\varphi _2} \end{array} $ | (1) |
式中,P1、P2为双频伪距观测值;φ1、φ2为载波相位观测值;a=f12/f22, f为载波频率。
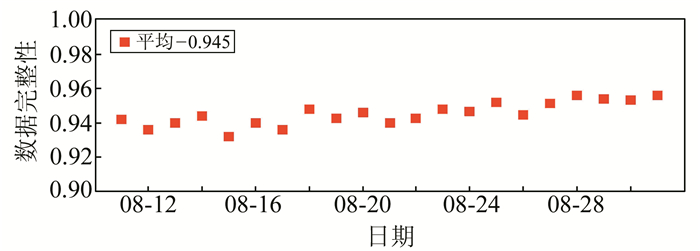
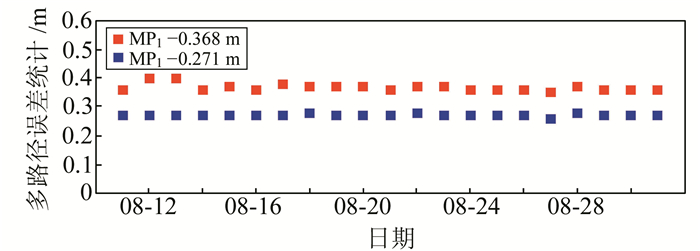
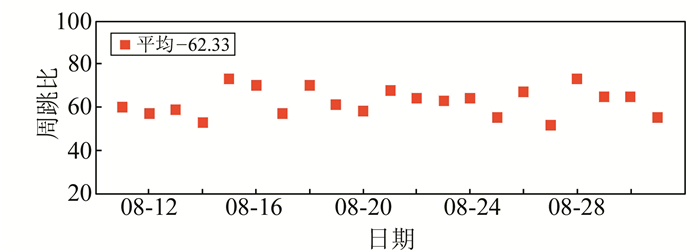
图 1~3给出了2016-08-11~08-31资源三号02星双频GPS数据统计结果。由图 1可知,观测数据完整性良好,平均为94.5%;图 2为观测数据P1和P2码上多路径效应误差,分别为0.368 m、0.271 m,整体上L2频率上的多路径误差比L1要大;图 3为周跳比统计结果,平均为62.33。
|
图 1 观测数据完整性统计 Fig. 1 The statistic of spaceborne GPS measurement |
|
图 2 观测数据的多路径效应误差统计 Fig. 2 The measurement statistics of P1 and P2 code |
|
图 3 观测数据周跳比统计 Fig. 3 The measurement statistics of cycle slips |
低轨卫星位于地球外200~2 000 km范围内绕地球运动,受到包括地球引力、日月引力、地球非球形摄动力、潮汐摄动、大气阻力、太阳辐射压、地球辐射压以及相对论效应等多种力的作用。结合牛顿定律,其运动微分方程可表示为:
| $ \ddot r =-{\rm{ }}\frac{{GM}}{{{r^3}}}r + {f_1}({t_1}, r, \dot r, {q_1}, \cdots {q_d}) $ | (2) |
式中,r、
假设先验轨道r0(t)为已知,动力法定轨可视为是一个改善轨道的过程。对r(t)进行泰勒级数展开,并消去未知扰动力参数部分,则真实轨道r(t)可由参数pi的先验值pi0表示:
| $ r\left( t \right) = {r_0}\left( t \right) + \sum\limits_{i = 1}^n {\frac{{\partial {r_0}\left( t \right)}}{{{\rm{ }}\partial {p_i}}}} \cdot({p_i}-{p_{i0}}) $ | (3) |
式中,pi为轨道参数;n=6+d表示未知参数的个数(6个初始轨道元素与d个动力参数)。
简化动力学方法在采用力学模型和数值积分求解轨道时引入伪随机脉冲参数来平衡观测数据和力学摄动对定轨结果的影响,即每隔一段时间在卫星径向、切向和法向上附加伪随机脉冲参数,如大气阻力摄动、相对论摄动以及地球红外辐射和地球反射压摄动等。
2.2 模型参数与数据策略定轨过程中采用的力学模型及参数见表 1,定轨数据来源见表 2。
|
|
表 1 力学模型及参数 Tab. 1 Mechanical model and parameters |
|
|
表 2 定轨数据来源 Tab. 2 Date used in orbit determination |
本文采用重叠弧段和卫星激光测距(SLR)检核两种方法来评估星载GPS数据简化动力学定轨结果。
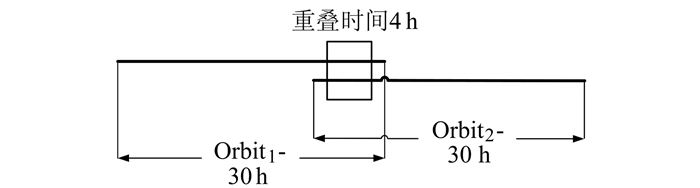
1) 重叠弧段精度分析。定轨弧段采用30 h,即每天00:00:00至第二天06:00:00,相邻定轨弧段有6 h重叠(图 4)。虽然重叠弧段的GPS观测数据是相同的,但是相邻两次精密定轨结果是独立的,可以用重叠弧段的比较结果来评估卫星的轨道精度。由于定轨弧段开始和结束的约束较弱,将Orbit1的后1 h数据和Orbit2的前1 h数据删除,取重叠弧段为4 h。
|
图 4 轨道重叠 Fig. 4 Sketch map of overlap orbit |
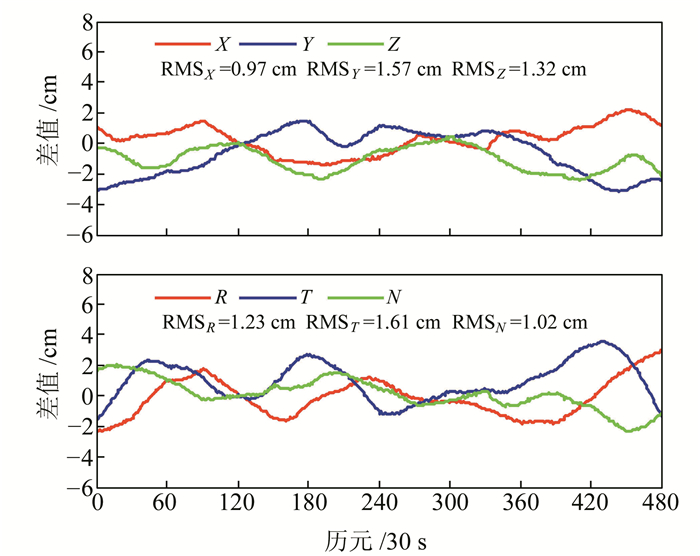
图 5为2016-08-11与2016-08-12定轨重叠弧段残差图。在地固系下,X方向残差值在-2~2 cm之间,RMS为0.97 cm;Y方向残差值在-3.20 ~1.50 cm之间,RMS为1.57 cm;Z方向残差值在-2.40~0.40 cm之间,RMS为1.32 cm。在星固系下,R(径向)方向残差值在-2.33~2.98 cm之间,RMS为1.23 cm;T(切向)方向残差值在-1.52~3.56 cm之间,RMS为1.61 cm;N(法向)方向残差值在-2.35~2.09 cm之间,RMS为1.02 cm。统计表明,两个定轨弧段的拟合效果较好,定轨结果可靠。
|
图 5 2016-08-11重叠弧段精度统计 Fig. 5 Orbit determination accuracy of overlapping arc from August 11 to 12, 2016 |
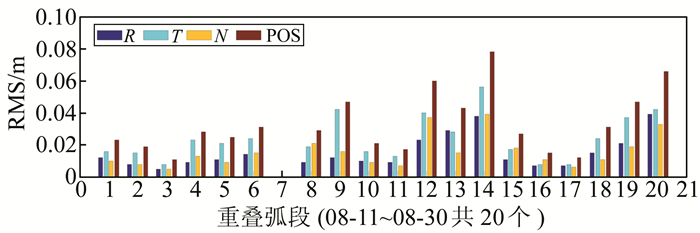
图 6为2016-08-11~31相邻定轨重叠弧段的精度统计。由图 6可知,R方向RMS最大为3.9 cm,最小为0.5 cm,平均为1.59 cm;T方向RMS最大为5.6 cm,最小为0.8 cm,平均为2.48 cm;N方向RMS最大为3.9 cm,最小为0.50 cm,平均为1.65 cm;三维位置精度在1.1~7.8 cm之间,平均为3.3 cm。由于重叠弧段的两次定轨相互独立,由误差传播定律,资源三号02星精密定轨精度为
|
图 6 2016-08-11~31重叠弧段精度统计 Fig. 6 Orbit determination accuracy of overlapping arc from August 11 to 31, 2016 |
2) SLR检核轨道。利用高精度的星载SLR观测数据对本文定轨结果进行外部检核。其中,SLR残差为SLR测得的站星距与星载GPS数据定轨结果计算的站星距之差,计算时需要考虑SLR观测数据和SLR测站的各项误差改正,包括对流层延迟改正、固体潮、海洋潮汐改正、相对论效应改正、卫星质心改正、测站偏心改正等。
跟踪资源三号02星的SLR站有3个:北京站(7249)、长春站(7237)和上海站(7821)。由于SLR观测受天气影响较大,截至2016-08-31,出现SLR跟踪间断。鉴于SLR观测数据量较少,本文在检核时未设置卫星截止高度角。
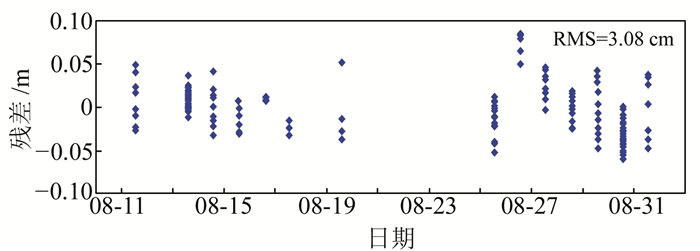
SLR观测时存在明显的系统误差。图 7为去除系统误差后SLR数据校轨结果,最大值为8.5 cm,最小为-6.0 cm,RMS为3.08 cm,检核结果较好。
|
图 7 资源三号02星SLR较轨结果 Fig. 7 The results of SLR validation for ZY3-02 satellite orbits |
对资源三号02星轨道进行预报是在轨检校和轨道监控的必要手段之一。本文采取两种方法对资源三号02星进行预报,通过预报精度对比验证预报方法的可靠性。
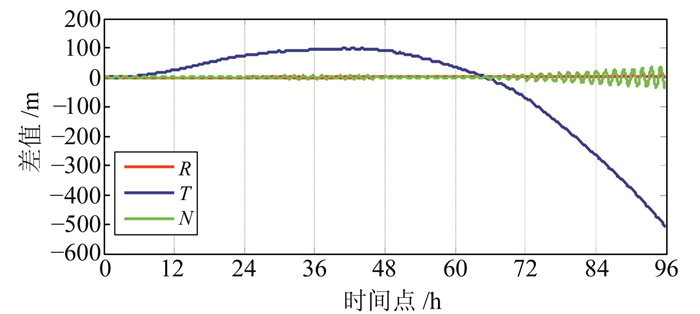
3.1 轨道外推根据星载GPS数据单天定轨结果进行轨道外推,外推弧长设为1 d,当天的伪随机脉冲参数和太阳辐射压参数与前一天相同,用于轨道积分的轨道根数由前一天最后一个历元的位置坐标计算得到。图 5为2016-08-11精密定轨结果外推08-12~16的轨道与精密定轨结果的差异对比。图 8表明,伪随机脉冲参数能够有效地拟合轨道,T(切向)方向变化明显,12 h内精度优于30 m,12 ~24 h精度为30~80 m。国内SLR观测站一般观测时间为12 ~24 h,该方法预报轨道精度满足SLR观测需要。同时,验证了本文定轨精度的精确性和可靠性。
|
图 8 资源三号02星外推轨道与精密轨道对比 Fig. 8 The results of SLR validation for ZY3-02 satellite orbits |
瞬时根数是根据卫星测轨技术计算的某个时刻卫星轨道根数。当星载GPS观测数据下传不稳定或者间断时,可以采用瞬时根数进行轨道预报。本文利用当天的轨道瞬时根数,采用两天前精密定轨的伪随机脉冲参数和太阳辐射压参数解算当天的卫星轨道。图 9为2016-08-11预报2016-08-11~13的卫星轨道与精密定轨结果的差异对比。由图可知,12 h内切向差值优于160 m,12 ~24 h精度在200 m左右。

|
图 9 瞬时根数预报轨道与精密轨道对比 Fig. 9 The results of SLR validation for ZY3-02 satellite orbits |
1) 资源三号02星快速轨道的重叠弧段径向精度在1.59 cm左右,切向精度在2.48 cm左右,法向精度在1.65 cm左右,三维位置精度优于5.52 cm。
2) 利用SLR观测数据对资源三号02星精密定轨结果进行检核,精度可达3 cm。
3) 基于星载GPS定轨结果的轨道预报精度优于基于瞬时根数的预报。由于星载数据下传出现延迟和间断,瞬时根数的方法可作为基于星载GPS定轨预报的辅助,同样满足SLR观测的需要。
4) 本文定轨结果达到cm级,短期预报结果可达m级,能够满足立体测图数据的应用需求和激光联测需要,为实现双星组网提供了精度依据。
致谢 感谢国家测绘地理信息局卫星测绘应用中心提供星载GPS观测数据。
| [1] |
Schutz B E, Tapley B D, Abusali P A M, et al. Dynamic Orbit Determination Using GPS Measurements from TOPEX/POSEIDON[J]. Geophysical Research Letters, 1994, 21(19): 2 179-2 182 DOI:10.1029/94GL01040
(  0) 0) |
| [2] |
Svehla D, Rothacher M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters[J]. Advances in Geosciences, 2003, 1(1): 47-56
(  0) 0) |
| [3] |
Luthcke S B, Zelensky N P, Rowlands D D, et al. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation[J]. Marine Geodesy, 2003, 26(3-4): 399-421
(  0) 0) |
| [4] |
Haines B, Desai S, Willis P, et al. Precise Orbit Determination for Jason-1: GPS and the 1-cm Challenge[C]. EGS - AGU - EUG Joint Assembly, 2003
(  0) 0) |
| [5] |
刘经南, 赵齐乐, 张小红. CHAMP卫星的纯几何定轨及动力平滑中的动力模型补偿研究[J]. 武汉大学学报:信息科学版, 2004, 29(1): 1-6 (Liu Jingnan, Zhao Qile, Zhang Xiaohong. Geometric Orbit Determination of CHAMP Satellite and Dynamic Models Compensation during Orbit Smoothing[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1): 1-6)
(  0) 0) |
| [6] |
李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨[J]. 科学通报, 2009, 35(6): 2 355-2 362 (Li Jiancheng, Zhang Shoujian, Zou Xiancai, et al. Zero-Difference Kinematic POD for GRACE at Centimeter-Level[J]. Chinese Science Bulletin, 2009, 35(6): 2 355-2 362)
(  0) 0) |
| [7] |
赵春梅, 唐新明. 基于星载GPS的资源三号卫星精密定轨[J]. 宇航学报, 2013, 34(9): 1202-1206 (Zhao Chunmei, Tang Xinming. Precise Orbit Determination for the ZY-3 Satellite Mission Using GPS Receiver[J]. Journal of Astronautics, 2013, 34(9): 1202-1206)
(  0) 0) |
| [8] |
赵春梅, 程鹏飞, 益鹏举. 基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011, 32(4): 762-766 (Zhao Chunmei, Cheng Pengfei, Yi Pengju. Reduced-Dynamics Satellite Orbit Determination Based on Pseudo-Stochastic Pulse Estimation[J]. Journal of Astronautics, 2011, 32(4): 762-766)
(  0) 0) |
| [9] |
余文坤, 戴吾蛟, 杨哲. 基于TEQC的GNSS数据质量分析及预处理软件的设计与实现[J]. 大地测量与地球动力学, 2010, 30(5): 81-85 (Yu Wenkun, Dai Wujiao, Yang Zhe. GNSS Data Analysis & Pre-Processing Software Design Based on TEQC[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 81-85)
(  0) 0) |
| [10] |
秦建, 郭金运, 孔巧丽, 等. Jason-2卫星星载GPS数据cm级精密定轨[J]. 武汉大学学报:信息科学版, 2014, 39(2): 137-141 (Qin Jian, Guo Jinyun, Kong Qiaoli, et al. Precise Orbit Determination of Jason-2 with Precision of Centimeters Based on Satellite-borne GPS Technique[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 137-141)
(  0) 0) |
| [11] |
盛传贞, 甘卫军, 赵春梅, 等. 不同观测技术的Jason-2卫星精密定轨评估[J]. 测绘学报, 2014, 15(8): 796-802 (Sheng Chuanzhen, Gan Weijun, Zhao Chunmei, et al. Assessment of Precise Orbit Determination of Jason-2 Satellite Using Different Observation Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 15(4): 796-802)
(  0) 0) |
| [12] |
林明森, 王晓慧, 彭海龙, 等. HY-2卫星双频GPS精密定轨技术[J]. 中国工程科学, 2014, 16(6): 97-101 (Lin Mingsen, Wang Xiaohui, Peng Hailong, et al. Precise Orbit Determination Technology Based on Dual-Frequency GPS Solution for HY-2 Satellite[J]. Engineering Sciences, 2014, 16(6): 97-101)
(  0) 0) |
| [13] |
彭冬菊, 吴斌. Jason-1卫星厘米级星载GPS精密定轨[J]. 科学通报, 2008, 53(21): 2 569-2 575 (Peng Dongju, Wu Bin. Precise Orbit Determination of Jason-1 with Precision of Centimeters Based on Satellite-Borne GPS Technique[J]. Chinese Science Bulletin, 2008, 53(21): 2 569-2 575)
(  0) 0) |
| [14] |
周旭华, 王晓慧, 赵罡, 等. HY2A卫星的GPS/DORIS/SLR数据精密定轨[J]. 武汉大学学报:信息科学版, 2015, 40(8): 1 000-1 005 (Zhou Xuhua, Wang Xiaohui, Zhao Gang, et al. The Precise Orbit Determination for HY2A Satellite Using GPS, DORIS and SLR Data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(8): 1 000-1 005)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. Satellite Surveying and Mapping Application Center, NASMG, 1 Baisheng Village, North-Sanhuqiao Road, Beijing 100830, China
 2018, Vol. 38
2018, Vol. 38

