2. 地理信息工程国家重点实验室,西安市雁塔路126号,710054
BDS实时精密定位通常采用短基线差分定位的方式,短基线差分定位的精度依赖于模糊度浮点解的精度和模糊度固定的准确性。在改善模糊度浮点解精度方面,针对快速定位的BDS双差法方程严重病态、最小二乘(LS)模糊度精度较差且协方差相关性强的问题,可利用正则化方法改善浮点模糊度的精度[1-2],进而利用LAMBDA方法进行模糊度搜索[3],确定正确的模糊度值。在模糊度固定方面,正确固定所有模糊度能够获得最优的定位精度。然而在某些条件下(如卫星刚升起、卫星信号发生粗差等),部分模糊度参数精度较差,正确固定所有模糊度较困难。同时,精度较差的模糊度将会影响整体模糊度的固定,导致该历元模糊度未能成功固定。
本文提出一种部分模糊度固定策略,能够有效控制非最优模糊度的影响,提高用户端模糊度固定的成功率[4]。最后,采用正则化方法和部分模糊度固定策略,利用香港卫星定位参考站网数据进行实时北斗差分定位系统的研究并进行验证。算例结果表明,本文提出的方法能有效提高BDS基线解算的精度。
1 BDS单历元基线解算原理对于双差相对定位,卫星钟差和接收机钟差能在双差过程中完全消除[5]。对于短基线,轨道误差和大气延迟(对流层延迟和电离层延迟)经双差处理后,影响也可以忽略不计[5]。
本文单历元基线解算采用非组合双差方式,固定的模糊度均为基频模糊度。为不失一般性,这里仅给出一个频点的双差观测方程。若仅利用相位观测值时,观测方程是秩亏的,可以引入伪距观测值来解决:
| $ \left. \begin{align} &\Delta \nabla P=\Delta \nabla \rho +{{e}_{1}} \\ &\Delta \nabla \varphi =\Delta \nabla \rho +\lambda \Delta \nabla N+{{e}_{2}} \\ \end{align} \right\} $ | (1) |
式中,Δ∇P为双差伪距观测值,Δ∇φ为载波相位双差观测值(单位m),Δ∇ρ为双差卫地距,λ为波长,Δ∇N为双差整周模糊度,e1、e2为双差观测值的随机噪声。
2 病态逆问题的正则化方法将式(1)线性化得:
| $ \mathit{\boldsymbol{y}}\text{ }=\left[\mathit{\boldsymbol{A}}\ \ \ \ \ \mathit{\boldsymbol{B}} \right]\left[\begin{align} &\mathit{\boldsymbol{X}} \\ &\mathit{\boldsymbol{n}} \\ \end{align} \right]+\mathit{\boldsymbol{e}} $ | (2) |
式中,y和e分别为观测向量和随机噪声向量,X和n分别为基线向量和模糊度向量,A和B分别为基线向量和模糊度向量的系数矩阵。令A′=[A B],x=[X n]T,如果A′病态,则小的观测误差会引起大的LS估值扰动。采用TIKHONOV正则化准则计算稳定的估值[6]:
| $ \|\mathit{\boldsymbol{{A}'x}}-\mathit{\boldsymbol{y}}{{\|}^{2}}+\alpha {{\mathit{\boldsymbol{x}}}^{\text{T}}}\mathit{\boldsymbol{x}}=\text{min}~ $ | (3) |
正则化解有偏,只有合理地确定正则化参数,才能有效地平衡观测值和偏差对解的贡献[6]。如果正则化参数过小,则无法有效地抑制观测噪声对解的影响;反之,正则化参数过大,则会降低观测值对解的贡献,导致解的偏差较大[6]。正则化参数的求解方法较多,如偏差原理法、广义交叉检核法(GCV)和L-曲线法等。其中,L-曲线法最常用,但其计算的参数往往偏大,导致过度正则化[7]。事实上,每种方法都有优缺点以及适用性,不存在某一个准则在所有场合都最优[8]。本文通过大量实验选取正则化参数α=1,此时正则化后的法方程为:
| $ \mathit{\boldsymbol{{N}'=}}\left[\begin{matrix} {{\mathit{\boldsymbol{A}}}^{\text{T}}}\mathit{\boldsymbol{PA}}+\mathit{\boldsymbol{I}}&{{\mathit{\boldsymbol{A}}}^{\text{T}}}\mathit{\boldsymbol{PB}} \\ {{\mathit{\boldsymbol{B}}}^{\text{T}}}\mathit{\boldsymbol{PA}}&{{\mathit{\boldsymbol{B}}}^{\text{T}}}\mathit{\boldsymbol{PB}} \\ \end{matrix} \right] $ | (4) |
对应的基线浮点解为:
| $ \mathit{\boldsymbol{x}}={{({{\mathit{\boldsymbol{A}}}^{\text{T}}}\mathit{\boldsymbol{PA}}+\mathit{\boldsymbol{I}})}^{-1}}~{{\mathit{\boldsymbol{A}}}^{\text{T}}}\mathit{\boldsymbol{Py}} $ | (5) |
利用TIKHONOV正则化修正后的模糊度浮点解作为模糊度搜索的浮点解,(ATPA+I)-1中模糊度对应的协方差阵作为模糊度搜索的协方差阵,组成模糊度搜索准则,利用LAMBDA方法进行搜索。
3 部分模糊度固定策略GNSS高精度定位中,模糊度参数的正确解算是关键。然而在某些条件下,正确固定所有模糊度(模糊度全集)较为困难,如卫星刚升起时受多路径和噪声影响较大,某颗卫星发生粗差导致模糊度浮点解不准确。这种条件下,若从模糊度全集中依据一定的准则选出质量较好的部分模糊度子集进行固定,反而能够提高模糊度的固定成功率[9]。鉴于此,本文提出一种质量控制的部分模糊度固定策略,按照一定的策略选出最优的模糊度子集进行固定:1)模糊度对应的卫星高度角应大于15°(可减小低高度角卫星受到的多路径和噪声影响,阈值可根据观测环境调整);2)观测数据发生粗差或周跳的卫星不参与模糊度固定。
文中提出的部分模糊度固定方法,不用对LAMBDA方法进行更改,只对实数模糊度和协方差进行调整,简单易行。具体算法如下。
设X1为不满足上述条件的次优模糊度子集和时变参数(如坐标参数等),X2为满足上述准则选出的最优模糊度子集。对式(1)采用正则化方法获取的法方程为:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}}_{11}}&{\mathit{\boldsymbol{N}}_{12}}\\ {\mathit{\boldsymbol{N}}_{21}}&{\mathit{\boldsymbol{N}}_{22}} \end{array}} \right]\left[ \begin{array}{l} {\mathit{\boldsymbol{X}}_1}\\ {\mathit{\boldsymbol{X}}_2} \end{array} \right] = \left[ \begin{array}{l} {\mathit{\boldsymbol{W}}_1}\\ {\mathit{\boldsymbol{W}}_2} \end{array} \right] $ | (6) |
令
| $ \mathit{\boldsymbol{Q=}}{{\left[\begin{matrix} \mathit{\boldsymbol{N}}_{11}&\mathit{\boldsymbol{N}}_{12} \\ \mathit{\boldsymbol{N}}_{21}&\mathit{\boldsymbol{N}}_{22} \\ \end{matrix} \right]}^{-1}}=\left[\begin{matrix} \mathit{\boldsymbol{Q}}_{11}&\mathit{\boldsymbol{Q}}_{12} \\ \mathit{\boldsymbol{Q}}_{21}&\mathit{\boldsymbol{Q}}_{22} \\ \end{matrix} \right] $ | (7) |
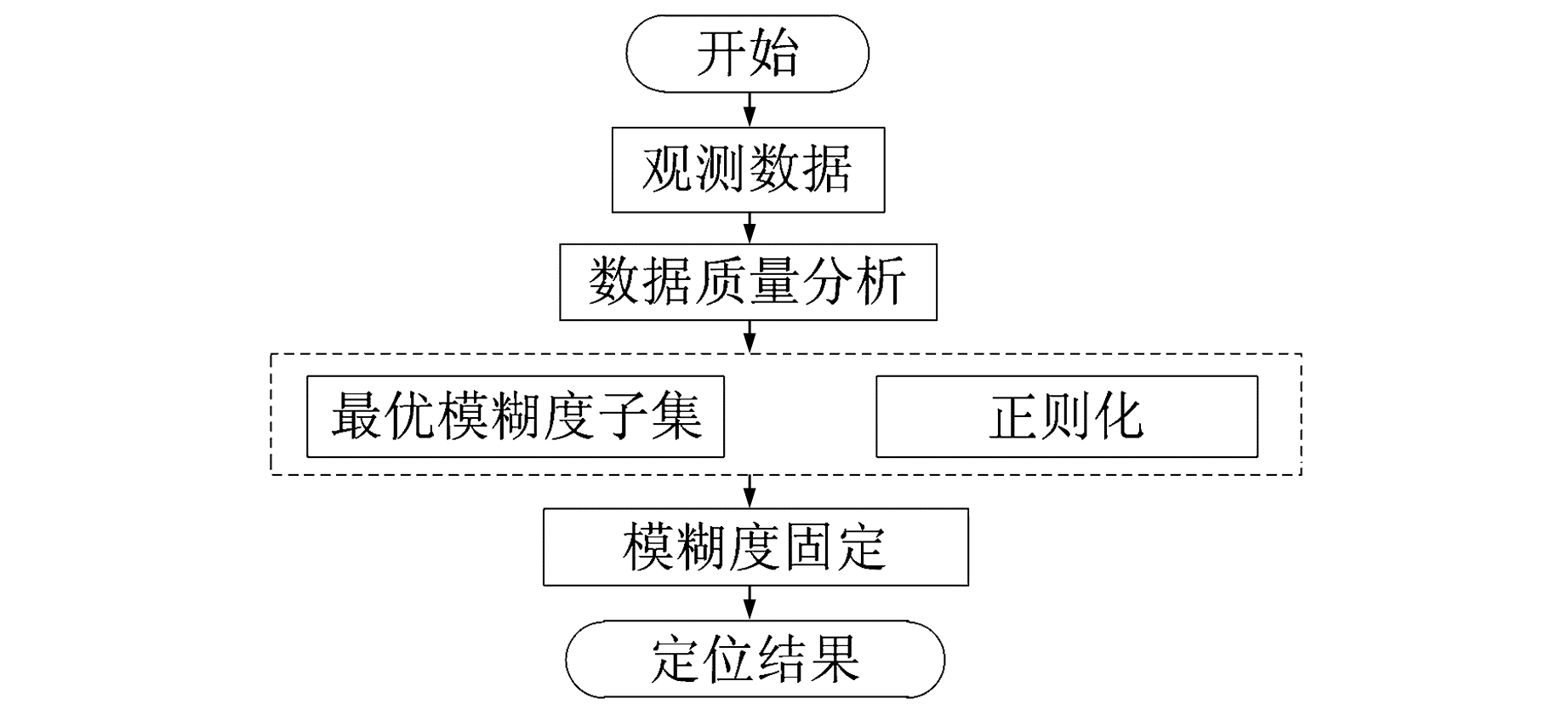
式中,Q为协方差阵, Q11和Q22分别为X1和X2对应的协方差阵。最后通过X2和Q22组成模糊度搜索准则,利用LAMBDA方法进行搜索固定X2,而不满足上述策略的模糊度只作为浮点解与基线向量一起解算。综合以上内容,可以得到BDS短基线单历元差分定位算法流程图,见图 1。
|
图 1 BDS短基线单历元差分定位算法流程 Fig. 1 Process of BDS short baseline single epoch differential positioning algorithm |
利用自主开发的软件计算香港卫星定位参考站网2016年第129天8个参考站22:00:00~22:59:59采样率为1 s的BDS数据,基线信息如表 1所示。下面通过算例1对TIKHONOV正则化方法的有效性进行验证;通过算例2对部分模糊度固定的效果进行分析。
|
|
表 1 基线信息 Tab. 1 Baseline information |
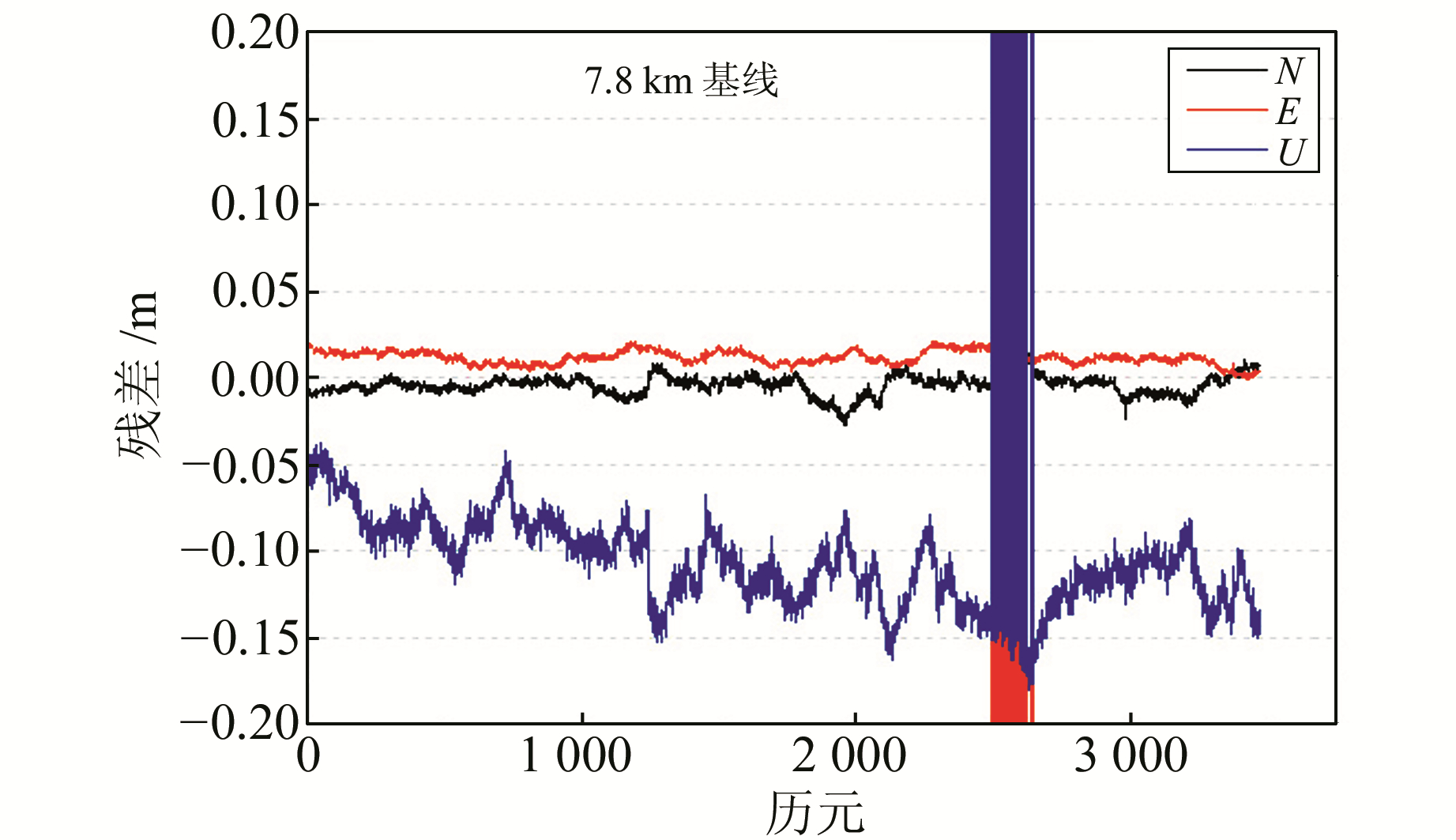
选择通过TIKHONOV正则化的方法与否,对基线2(可视卫星数为8颗)进行解算(经验证,基线1和基线3不存在病态问题),得到的基线残差结果见图 2和图 3(各历元解算结果的残差换算至平面与高程方向,下同)。
|
图 2 未进行正则化的定位结果残差 Fig. 2 Positioning results residuals before regularization |

|
图 3 进行正则化的定位结果残差 Fig. 3 Positioning results residuals after regularization |
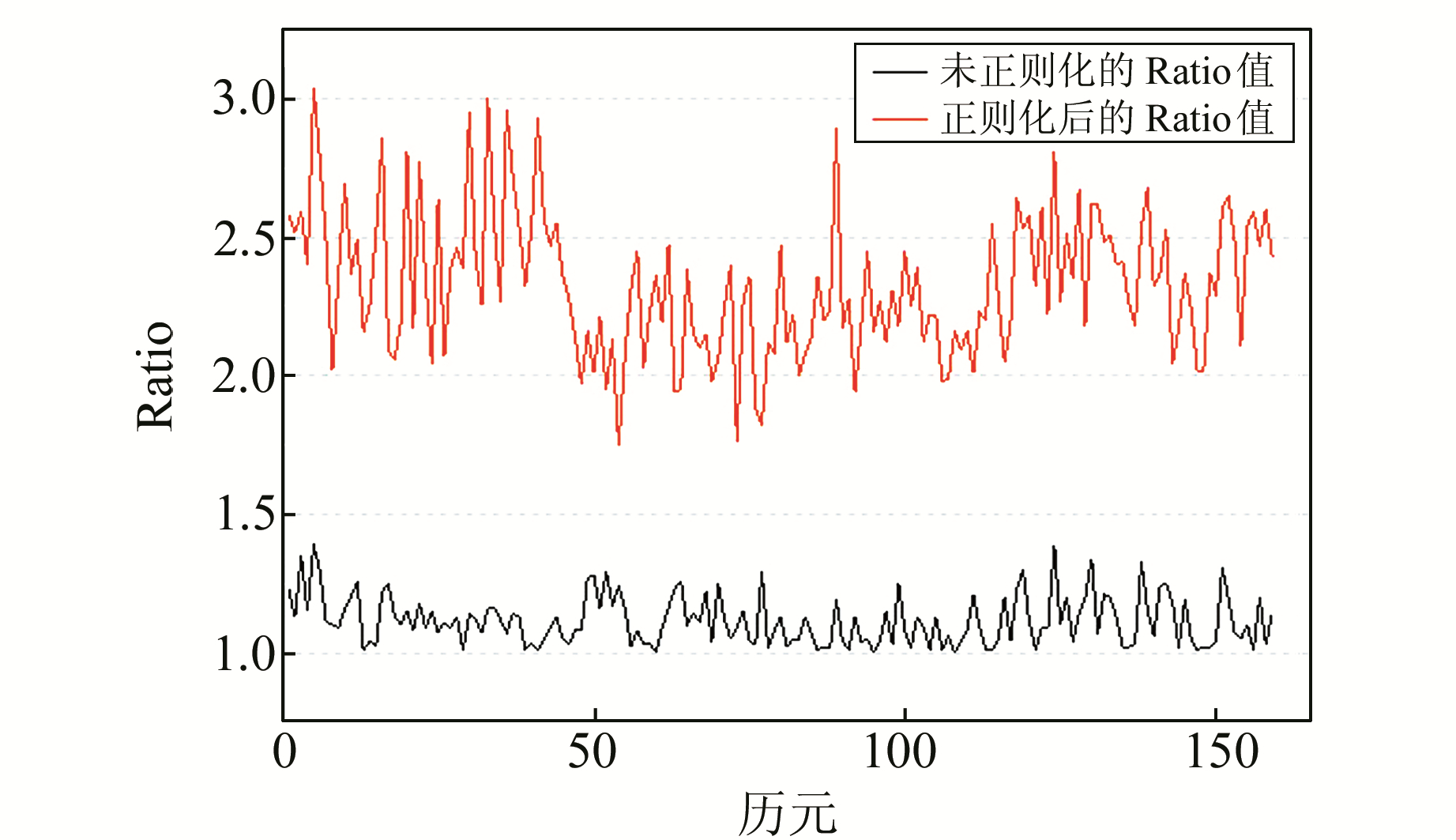
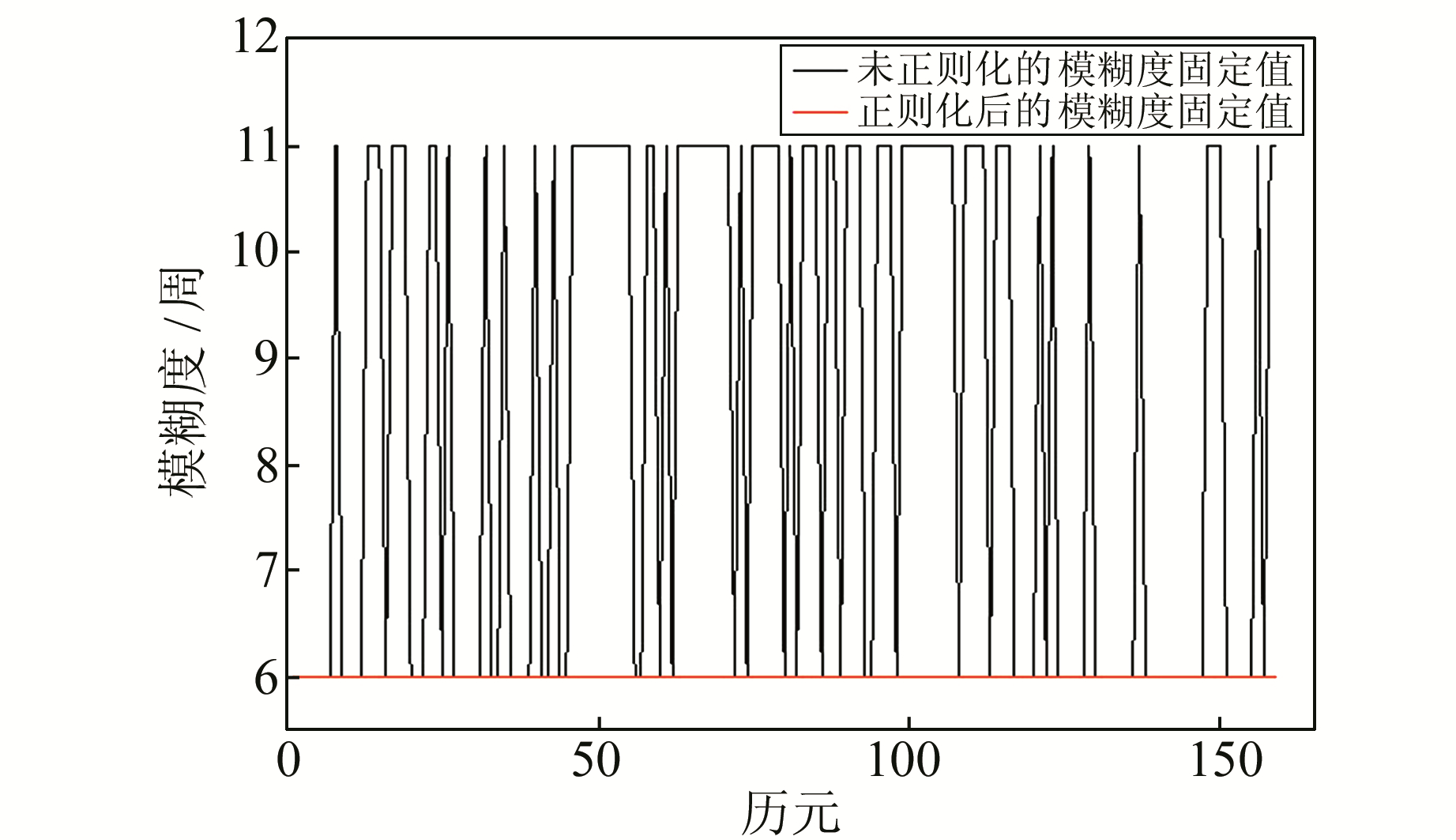
由图 2和图 3对比可知,未进行TIKHONOV正则化的定位结果存在部分异常,而且高程方向定位结果不稳定。因此,在定位异常处,分析Ratio值和模糊度固定结果发现,在22:43:16~22:45:47时间段,卫星组C07~C14的模糊度固定结果出现异常。将未进行TIKHONOV正则化和进行TIKHONOV正则化的结果进行对比。由图 4可以看出,TIKHONOV正则化后,Ratio值增大1倍,说明模糊度固定值较可靠。由图 5可知,TIKHONOV正则化后,模糊度固定值稳定在6周(与真值相符),所以TIKHONOV正则化方法提高了模糊度固定的准确性。
|
图 4 正则化前后的Ratio值 Fig. 4 The Ratio before and after regularilization |
|
图 5 正则化前后的模糊度固定值 Fig. 5 The fixed ambiguity before and after regularilization |
通过基线1和基线3(可视卫星数均为8颗)对部分模糊度固定策略的有效性进行分析。图 6和图 7是未采用部分模糊度固定策略(高度角较低和发生周跳粗差的卫星不参与模糊度固定)的定位结果残差,图 8和图 9是采用部分模糊度固定策略的定位结果残差。

|
图 6 定位结果残差 Fig. 6 Positioning results residuals |
|
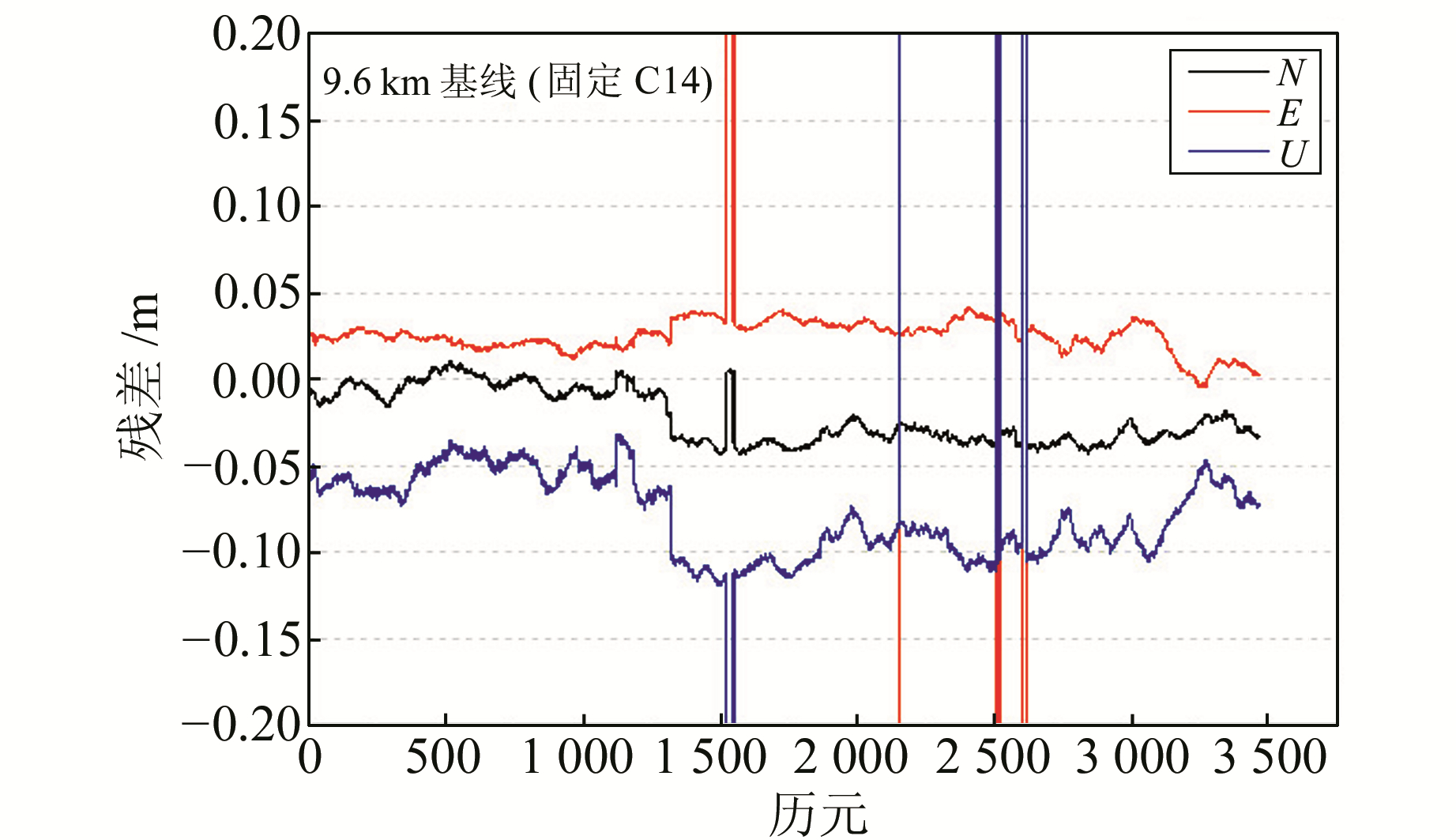
图 7 定位结果残差 Fig. 7 Positioning results residuals |
|
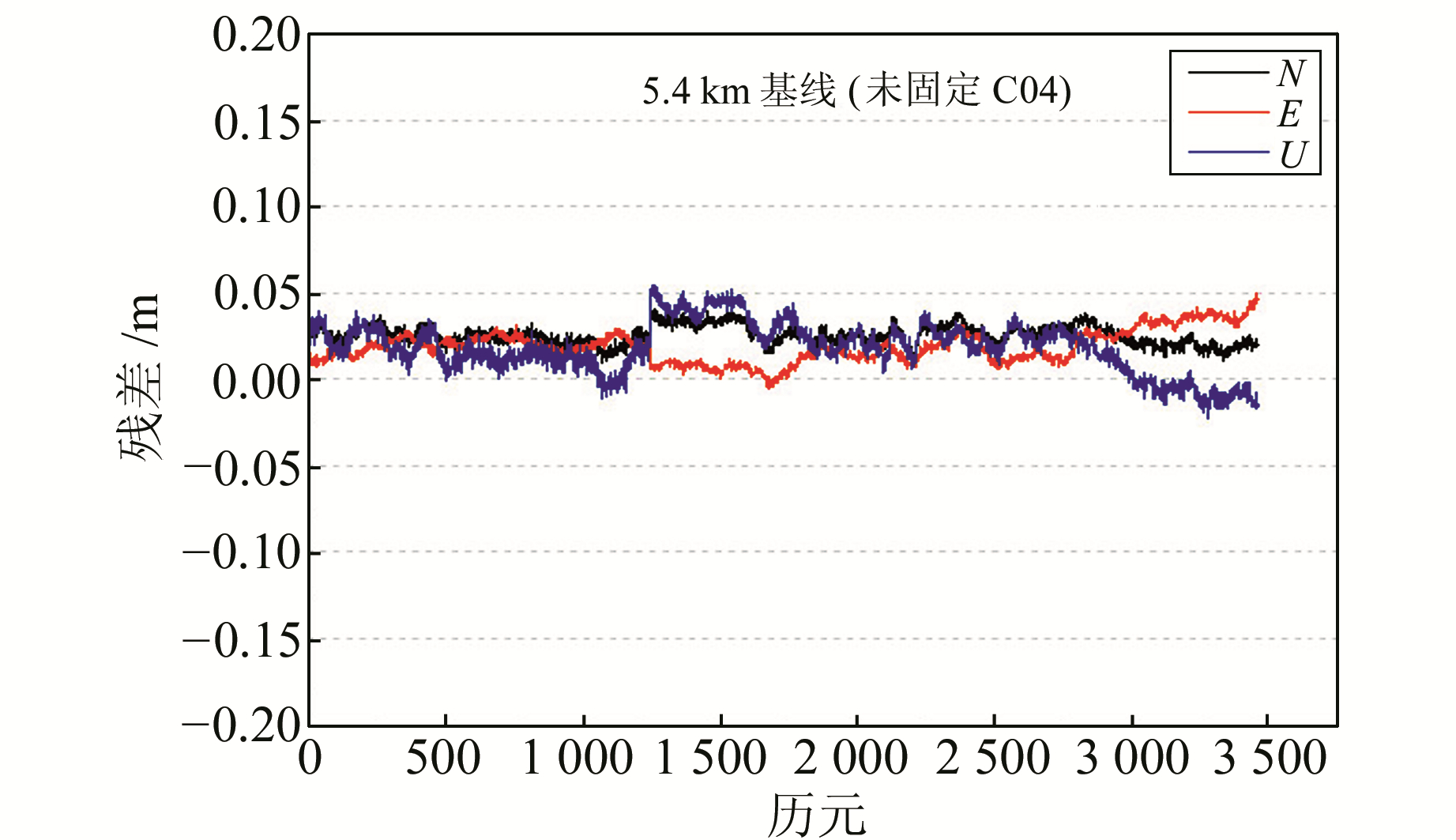
图 8 定位结果残差 Fig. 8 Positioning results residuals |

|
图 9 定位结果残差 Fig. 9 Positioning results residuals |
对比图 6、图 8及图 7、图 9可知,采用部分模糊度固定策略(未固定高度角较低的卫星C04和C14的模糊度)能有效控制非最优模糊度的影响,提高基线定位结果的精度。
5 结语目前亚太区域BDS观测卫星数保持在7~8颗以上,已具备区域高精度定位的能力。对于短基线单历元差分定位法方程病态性,可以利用TIKHONOV正则化方法进行有效的改善,进而使用LAMBDA方法进行模糊度搜索,得到可靠的固定解。在部分模糊度精度较差、难以正确固定时,本文采用的部分模糊度固定策略能有效控制非最优模糊度的影响。两种策略综合使用,可以使得北斗系统定位解算精度在平面和高程上均优于2 cm。
本文算例仅包括短基线,对于中长距离基线需要进一步讨论。
致谢 感谢香港地政总署提供数据。
| [1] |
孔令杰, 黄观文. 基于TIKHONOV正则化的短基线单历元模糊度解算方法研究[J]. 大地测量与地球动力学, 2010, 30(2): 148-155 (Kong Lingjie, Huang Guanwen. On Single Epoch Ambiguity Resolution of Short Baseline Based on TIKHONOV Regularilization[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 148-155)
(  0) 0) |
| [2] |
王振杰, 欧吉坤, 柳林涛. 单频GPS快速定位中病态问题的解法研究[J]. 测绘学报, 2005, 34(3): 196-201 (Wang Zhenjie, Ou Jikun, Liu Lintao. Investigation on Solutions of Ill-Conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 196-201)
(  0) 0) |
| [3] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1): 65-82
(  0) 0) |
| [4] |
潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1 210-1 217 (Pan Zongpeng, Chai Hongzhou, Liu Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-Difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1 210-1 217)
(  0) 0) |
| [5] |
张勤, 李家权. GPS测量原理及应用[M]. 北京: 科学出版社, 2005 (Zhang Qin, Li Jiaquan. Principle and Application of GPS Surveying[M]. Beijing: Science Press, 2005)
(  0) 0) |
| [6] |
李博峰. 混合整数GNSS函数模型及随机模型参数估计理论与方法[D]. 上海: 同济大学, 2010 (Li Bofeng. Theory and Method of Parameter Estimation for Mixed Integer GNSS Stochastic and Function Models [D]. Shanghai: Tongji University, 2010) http://kns.cnki.net/KCMS/detail/detail.aspx?filename=chxb201003024&dbname=CJFD&dbcode=CJFQ
(  0) 0) |
| [7] |
徐天河, 杨元喜. 抗差TIKHONOV正则化方法及其应用[J]. 武汉大学学报:信息科学版, 2003, 28(6): 719-722 (Xu Tianhe, Yang Yuanxi. Robust TIKHONOV Regularization Method and Its Applications[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 719-722)
(  0) 0) |
| [8] |
沈云中, 许厚泽. 不适定方程正则化解的谱分解式[J]. 大地测量与地球动力学, 2002, 22(3): 10-14 (Shen Yunzhong, Xu Houze. Spectral Decomposition Formula of Regularization Solution for Ill-Posed Equation[J]. Journal of Geodesy and Geodynamics, 2002, 22(3): 10-14)
(  0) 0) |
| [9] |
Brack A. On Reliable Data-Driven Partial GNSS Ambiguity Resolutions[J]. GPS Solutions, 2015, 19(3): 411-422 DOI:10.1007/s10291-014-0401-9
(  0) 0) |
2. State Key Laboratory of Geographic Information Engineering, 126 Yanta Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38


