2. 信息工程大学导航与空天目标工程学院,郑州市科学大道62号,450001;
3. 95806部队,北京市,100076
自1990年Schildknecht等提出利用GPS码伪距和载波相位组合观测量进行时间传递的设想以来,文献[1-3]对GPS载波相位时频传递算法进行研究,文献[4]对GLONASS时间传递算法进行研究,文献[5]对GPS/GLONASS组合载波相位时频传递进行研究。但由于GPS、GLONASS分别受美国和俄罗斯国防部控制,其可在必要时伪造甚至局部停发信号,因此研究BDS时频传递技术具有重要意义。目前,针对BDS的研究主要集中在RDSS单向、双向时间传递及共视时间传递[6-9]。RDSS单向时间传递精度较低;双向时间传递在水下潜艇等一些特殊场合有重要作用,但用户有限[8-9]; BDS共视时间传递可获得优于1 ns的精度,但需要两测站同时观测同一颗卫星,精度还会随测站向距离的增加而降低[6-7]。载波相位时间传递具有精度高、操作灵活方便的优点,有必要对BDS载波相位时频传递性能进行研究。
1 载波相位时间传递模型GNSS载波相位时间传递主要采用精密单点定位(PPP)算法[10]。BDS PPP与GPS PPP类似,通常采用双频消电离层组合。BDS具有三频信号,采用B1、B2频点的数据进行组合。观测方程如下:
| $ \begin{array}{l} {\mathit{\Phi }^j} = {\rho ^j} - c \cdot \delta t + c \cdot \delta {t^j} + \lambda \cdot {N^j} + {T^j} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{d_{{\rm{hd}}(\mathit{\Phi })}} - d_{{\rm{hd}}\left( \mathit{\Phi } \right)}^j + \varepsilon _\mathit{\Phi }^j \end{array} $ | (1) |
| $ \begin{array}{l} {P^j} = {\rho ^j} - c \cdot \delta t + c \cdot \delta {t^j} + {T^j} + {d_{{\rm{hd}}(\mathit{P})}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; - d_{{\rm{hd}}\left( \mathit{P} \right)}^j + \varepsilon _P^j \end{array} $ | (2) |
式中,j为卫星号,Φ和P分别为载波相位和伪距消电离层组合观测量,ρ为卫星天线相位中心到接收机天线相位中心的几何距离,c为光速,δt、δtj分别为接收机和卫星钟差,λ为消电离层组合载波波长,N为消电离层组合模糊度,T为对流层延迟,dhd(Φ)、dhd(P)为接收机端载波、伪距硬件延迟,dhd(Φ)j、dhd(P)j为卫星端载波、伪距硬件延迟,εΦj、εPj分别为载波和伪距测量噪声。
观测方程中卫星轨道和钟差采用GFZ提供的精密轨道和钟差产品内插得到。三维测站坐标、天顶对流层延迟作为未知参数进行估计,地球自转、相对论效应、天线相位缠绕、固体潮采用模型进行改正,模糊度参数采用浮点解。若接收机观测到m颗卫星,对观测模型进行线性化,可写成矩阵形式:
| $ \underset{2m\times 1}{\mathop{\mathit{\boldsymbol{Y}}}}\,=\underset{2m\times \left( m+5 \right)}{\mathop{\mathit{\boldsymbol{H}}}}\,\cdot \underset{\left( m+5 \right)\times 1}{\mathop{\mathit{\boldsymbol{X}}}}\,+\underset{2m\times 1}{\mathop{\mathit{\boldsymbol{ }}\!\!\varepsilon\!\!\rm{ }}}\,\nu \tilde{\ }N(0,{{\mathit{\boldsymbol{Q}}}_{y}}) $ | (3) |
| $ \mathit{\boldsymbol{X}} = [X, Y, Z, c\delta t, ztd, {N^1}, {N^2}, \cdots, {N^m}] $ | (4) |
式中,Y为观测向量,H为系数矩阵,X为未知参数向量,X、Y、Z为接收机三维坐标,ztd为天顶对流层延迟,其他参数含义同上。Qy为观测量的协方差矩阵,其元素Qii=a2+b2/sin2(E),E为卫星高度角,对于伪距观测量a=b=3 dm,对于载波相位观测量a=b=3 mm。
通过参数估计可解得接收机钟差参数δt。由于GNSS测量的是测站与卫星之间的相对时间,各分析中心发布的精密卫星钟差产品都是相对于参考时间(REFT,通常为GNSS系统时间)的相对钟差,采用PPP得到的钟差δt是测站相对于参考时间的相对钟差,解得δt即可实现接收机钟与参考时间(REFT)的同步。设测站接收机真实时间为T,参考时间为TREFT,则:
| $ \delta t = T - {T_{{\rm{REFT}}}} $ | (5) |
为分析BDS载波相位时频传递性能,对比BDS、GPS和GLONASS载波相位时频传递结果。选取2016-01-13澳大利亚卡拉特哈(KARR)和瓦努阿图首府维拉港(PTVL)站的数据进行分析。两测站均采用TRIMBLE NET R9接收机,可以接收所有卫星导航系统可用频率的信号,包括BDS(B1、B2、B3)、GLONASS(L1、L2、L3)、GPS(L1、L2、L5)、Galileo(E1、E5a、E5b)和QZSS(L1、L2、L5)[11]。数据来源于全球多系统定位服务实验网(Multi-GNSS experiment,MGEX),观测数据采样间隔为30 s,精密卫星轨道和钟差采用GFZ提供的5 min采样间隔的综合精密轨道和30 s采样间隔的综合精密钟差产品。
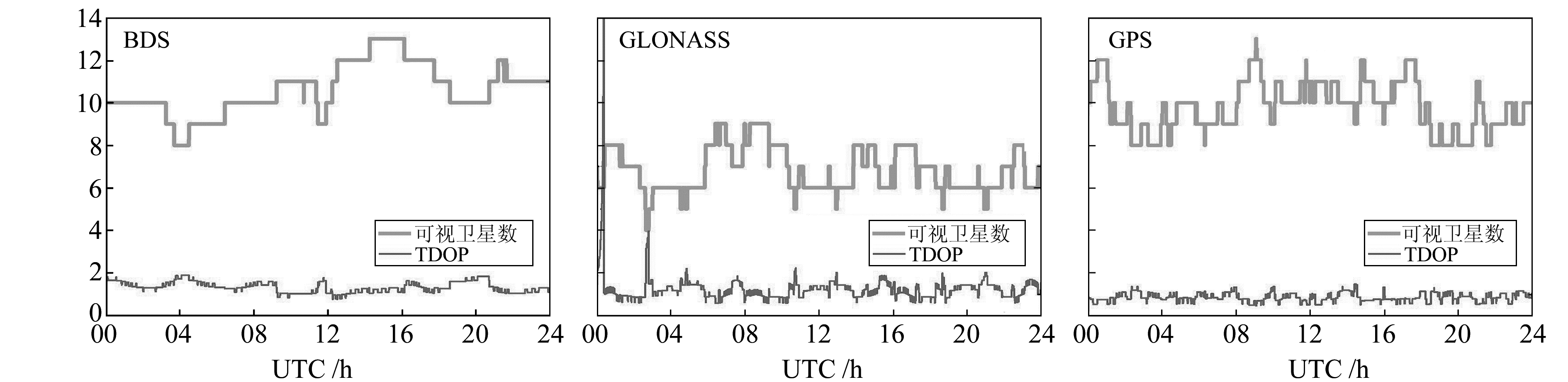
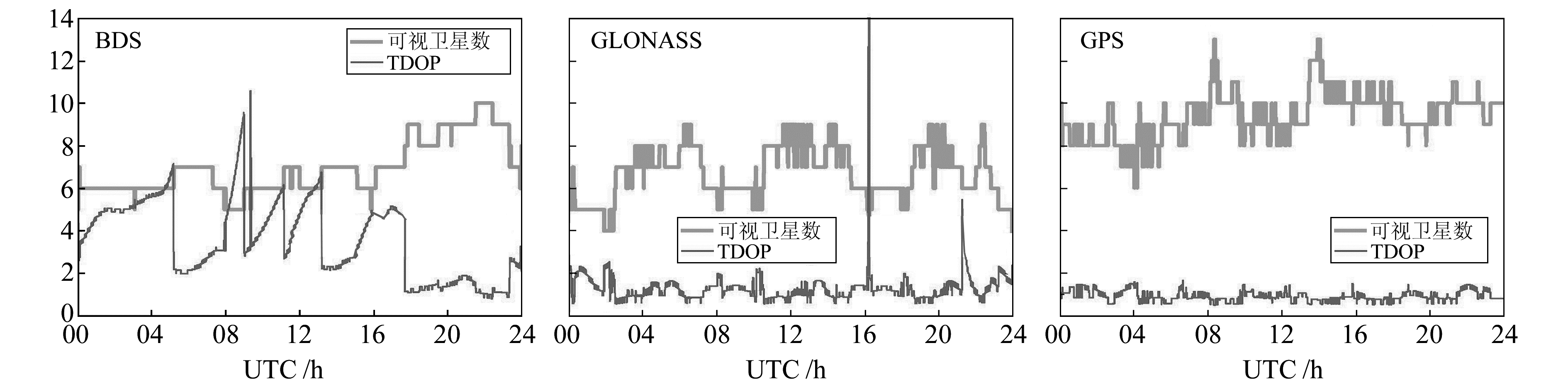
实验中卫星高度截止角设为7°,图 1、图 2分别给出了KARR和PTVL两测站BDS、GPS和GLONASS的可视卫星数和时间精度衰减因子(TDOP),表 1给出了BDS、GPS和GLONASS的平均可视卫星数和TDOP值。
|
图 1 KARR站3个系统的可视卫星数和TDOP Fig. 1 Satellite visibility and TDOP of three system constellations at KARR |
|
图 2 PTVL站3个系统的可视卫星数和TDOP Fig. 2 Satellite visibility and TDOP of three system constellations at PTVL |
|
|
表 1 平均可视卫星数和TDOP值 Tab. 1 The average value of satellite visibility and TDOP |
由图 1、图 2及表 1可知,KARR站BDS平均可视卫星数为10.1,与GPS基本相当,多于GLONASS的6.8颗。KARR站GPS的TDOP值最优为0.9,BDS在可视卫星数多于GLONASS的情况下TDOP与GLONASS相当,相对于GLONASS并没有明显提升。对于PTVL站,BDS平均可视卫星数较少,为6.9颗,平均TDOP值仅为3.5,在与GLONASS卫星数量基本相同的情况下TDOP值比GLONASS要差。这主要是因为目前BDS的MEO卫星数目较少,测站的可视卫星大部分为GEO、IGSO卫星,总体上的空间结构反而不如GPS和GLONASS。GPS和GLONASS的可视卫星在不同测站分布相对均匀,BDS在不同地区可视卫星数差别略大,这主要是因为BDS目前是区域系统,还未建成覆盖全球的卫星导航系统。
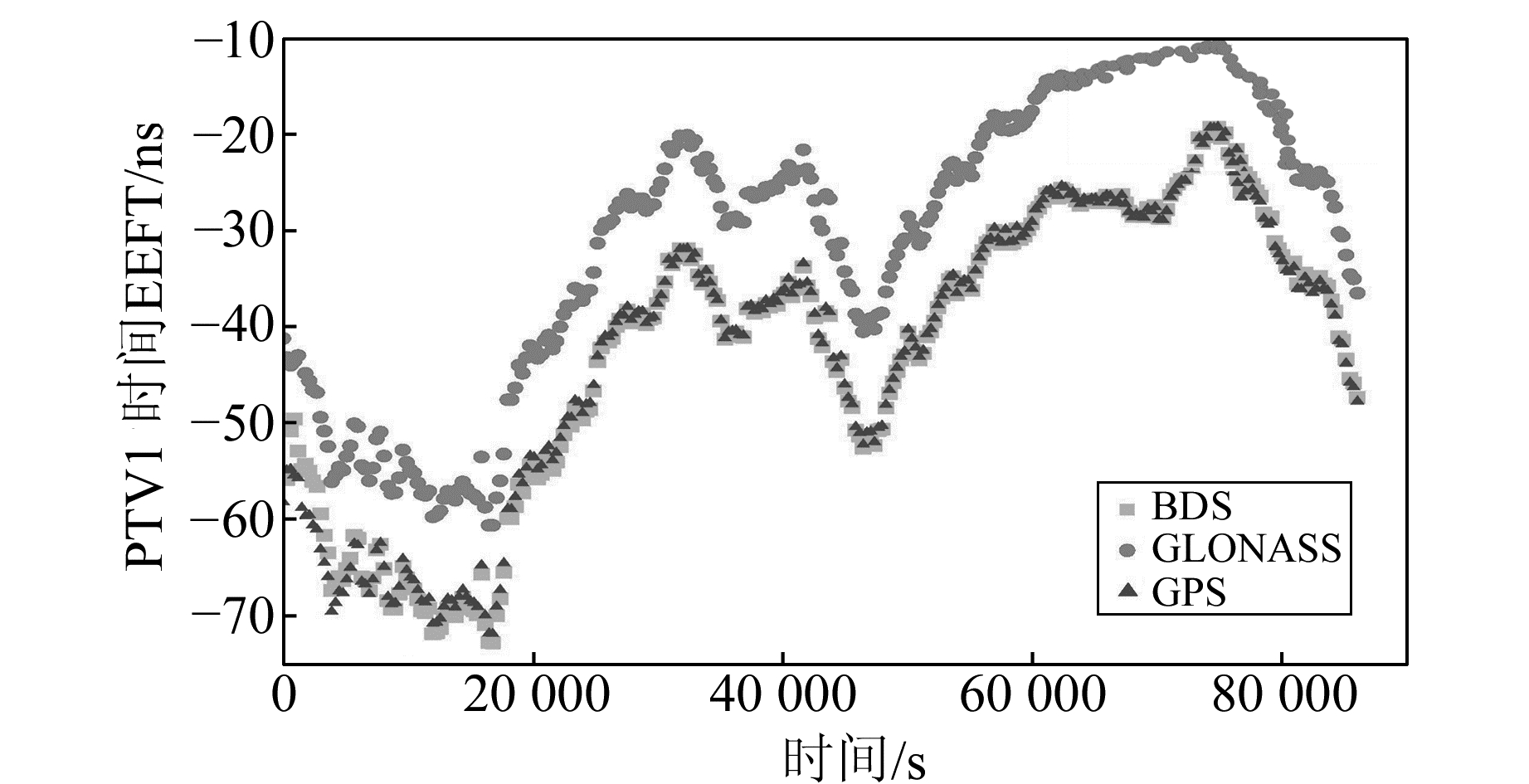
分别采用BDS、GPS和GLONASS观测量,使用前向Kalman滤波可得各站相对于参考时间的时间传递结果,如图 3、图 4所示。

|
图 3 KARR-REFT的时间传递结果 Fig. 3 Time transfer results of KARR-REFT |
|
图 4 PTVL-REFT的时间传递结果 Fig. 4 Time transfer result of PTVL-REFT |
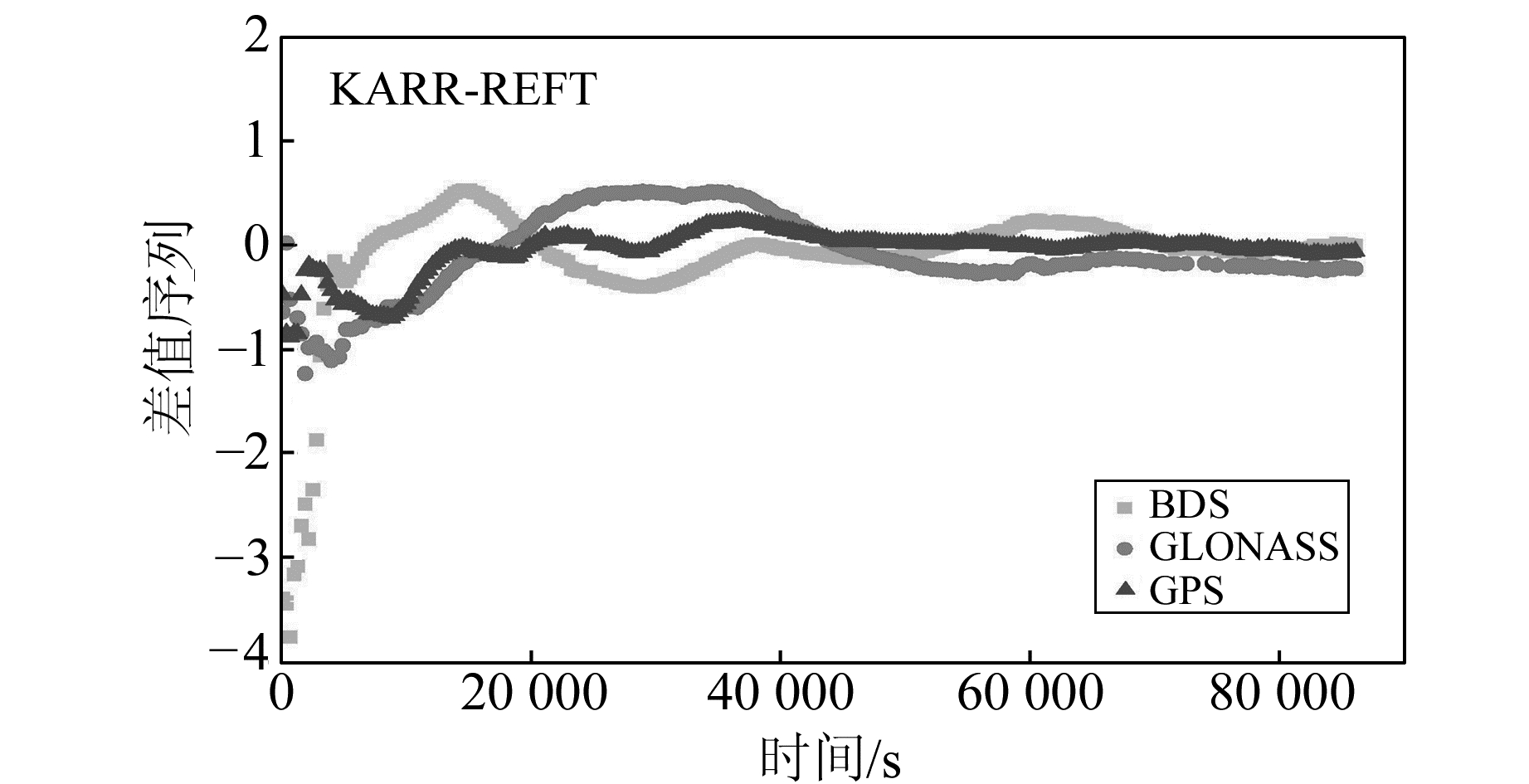
由图 3、图 4可知,测站KARR和PTVL的BDS、GPS和GLONASS的时间传递结果变化趋势十分一致,但不同系统间存在系统性偏差,不同测站系统偏差不同,这主要是由于不同系统卫星信号在接收机内部的硬件延迟不同所造成的,且不同卫星导航系统时间存在一定偏差,采用不同的模型和处理方法也会使结果存在一定的固定系统偏差。为了进一步分析各系统载波相位时间传递的性能,引入GFZ发布的网解钟差作为真值,将各系统结果与GFZ网解结果作差,可得到相应的差值序列。因GFZ只发布了5 min的网解结果,故以5 min为采样间隔进行分析。表 2(单位ns)给出了收敛后的精度统计结果,图 5、图 6给出去掉收敛后平均值的差值序列。
|
|
表 2 时间传递精度结果 Tab. 2 Accuracy of time transfer |
|
图 5 KARR-REFT减去平均值后的差值序列 Fig. 5 Difference sequence of KARR-REFT after removing the mean value |

|
图 6 PTVL-REFT减去平均值后的差值序列 Fig. 6 Difference sequence of PTVL- REFT after removing the mean value |
由图 5、图 6知,BDS能够用来进行时间传递,但BDS收敛速度较慢,明显长于GPS和GLONASS。这一方面是因为BDS跟踪站数量有限,导致其卫星精密轨道和钟差产品精度有限;另一方面可能是因为目前BDS星座主要由GEO和IGSO卫星构成,MEO卫星数较少,而GEO卫星相对地球位置变化较小,卫星空间几何结构变化缓慢,模糊度参数需要较长时间才能收敛。KARR站由于观测到的BDS卫星较多,其时间传递精度可以达到0.2 ns,与GPS和GLONASS基本相当。PTVL站由于观测到的BDS卫星相对较少,且几乎全部是GEO和IGSO卫星,空间构型较差,导致最终时间传递精度仅为0.68 ns,明显差于GPS和GLONASS。
利用GNSS载波相位观测量获得时间传递结果后,根据频率计算公式可得到相应的频率传递结果:
| $ y\left( t \right) = \left[{\delta \left( t \right)-\delta \left( {t-\mathit{\Delta } T} \right)} \right]/\mathit{\Delta } T $ | (6) |
式中,y为频率,ΔT为采样间隔(文中取300 s)。
图 7、图 8给出了KARR和PTV1的频率传递结果。为了更好地对比显示各方案得到的频率传递结果,图中分别对GLONASS、GPS和GFZ得到的频率传递结果加上4×10-11、-4×10-11、-8×10-11。表 3(单位10-12)给出了各频率传递结果的标准差。

|
图 7 KARR-REFT频率传递结果 Fig. 7 Frequency transfer solution of KARR-REFT |

|
图 8 PTVL-REFT频率传递结果 Fig. 8 Frequency transfer solution of PTVL-REFT |
|
|
表 3 频率传递结果的标准差 Tab. 3 Standard deviation of frequency transfer solution |
由图 7、图 8及表 3可知,BDS、GLONASS、GPS及GFZ的频率传递序列变化趋势十分一致,结果基本相当。对比文献[12]可知,本文解算的频率结果相对较差,这主要是因为测站KARR、PTVL均未配备高稳定度的原子钟作为外接频标,使用的是接收机内部时钟。而载波相位时频传递精度不仅由解算算法的精度决定,还取决于接收机钟的稳定性。为了从频率稳定度进一步分析各系统的时间传递性能,采用阿伦方差来计算频率稳定度:
| $ \begin{array}{l} \sigma _y^2\left( \tau \right) = \frac{1}{{2\left( {N - 2m} \right){\tau ^2}}}\cdot\\ \sum\limits_{i = 1}^{N - 2m} {{{[{x_{i + 2m}}-2{x_{i + m}} + {x_i}]}^2}} \end{array} $ | (7) |
式中,xi为历元i对应的钟差数据;τ=mτ0为取样时间;N为采样个数;m为钟差平滑因子,一般取
表 4给出了KARR和PTVL的BDS、GLONASS、GPS及GFZ的频率稳定度结果。由表 4可知,BDS与GLONASS、GPS及GFZ频率稳定度变化趋势完全一致,精度基本相当。但因测站KARR和PTVL接收机均未配备高稳定度的原子钟作为外接频标,解算得到的频率稳定度较差。
|
|
表 4 频率稳定性结果 Tab. 4 Frequency stability result |
本文利用GFZ发布的卫星精密产品和测站KARR、PTVL观测数据,以GPS、GLONASS载波相位时频传递为参考,分析BDS系统的时频传递性能。结果表明,BDS可以独立进行时间频率传递,但时频传递的收敛速度明显慢于GPS、GLONASS。在KARR站BDS可视卫星数较多(平均为10.1颗)的情况下,BDS时间传递性能同GPS、GLONASS基本相当;在PTVL站BDS可视卫星较少(平均为6.9颗)的情况下,TDOP大于GPS和GLONASS,时间传递精度差于GPS和GLONASS。两测站三系统频率传递结果和频率稳定度结果基本相当,变化趋势十分一致。时频传递精度由解算方法和接收机钟的频率稳定性共同决定,因测站KARR、PTVL均未配备高稳定度的原子钟作为外接频标,导致频率传递结果及频率稳定度结果相对较差。随着BDS导航卫星和全球跟踪站陆续增多,BDS空间几何结构将会显著改善,BDS精密产品的精度以及时频传递性能也将得到进一步提高。
| [1] |
Dach R, Beutler G, Hugentobler U, et al. Time Transfer Using GPS Carrier Phase Error Propagation and Results[J]. Journal of Geodesy, 2003, 77: 1-14 DOI:10.1007/s00190-002-0296-z
(  0) 0) |
| [2] |
Petit G, Kanj A, Loyer S, et al. 1 × 10-16 Frequency Transfer by GPS PPP with Integer Ambiguity Resolution[J]. Metrologia, 2015, 52(2): 1-4
(  0) 0) |
| [3] |
Cerretto G, Perucca A, Tavella P, et al. Network Time and Frequency Transfer with GNSS Receivers Located in Time Laboratories[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2010, 57(6): 1 276
(  0) 0) |
| [4] |
Jiang Z, Lewandowski W. Accurate GLONASS Time Transfer for the Generation of the Coordinated Universal Time[J]. International Journal of Navigation & Observation, 2012, 1 687-5 990
(  0) 0) |
| [5] |
Defraigne P, Harmegnies A, Petit G. Time and Frequency Transfer Combining GLONASS and GPS Data[C]. Frequency Control Symposium & the European Frequency and Time Forum, IEEE, 2011
(  0) 0) |
| [6] |
Kong Y, Yang X, Chang H, et al. Method of Precise Common-ViewFrequency Transfer Based on Beidou GEO Satellite[C]. Frequency Control Symposium IEEE, 2014
(  0) 0) |
| [7] |
Yi H, Wang H, Zhang S, et al. Research on Time and Frequency Transfer Based on Beidou Common View[C]. Frequency Control Symposium & the European Frequency and Time Forum, IEEE, 2015
(  0) 0) |
| [8] |
吴海涛, 李变, 武建锋. 北斗授时技术及其应用[M]. 北京: 电子工业出版社, 2016 (Wu Haitao, Li Bian, Wu Jianfeng. Beidou Timing Technology and Its Application[M]. Beijing: Electronic Industry Press, 2016)
(  0) 0) |
| [9] |
沙海, 占建伟, 王建辉, 等. 北斗卫星导航系统授时方法的比较与研究[C]. 中国卫星导航学术年会, 武汉, 2013 (Sha Hai, Zhan Jianwei, Wang Jianhui. Research and Compare of Timing Method Application for Compass Satellite Navigation System[C]. China Satellite Navigation Conference, Wuhan, 2013)
(  0) 0) |
| [10] |
于合理, 郝金明, 谢建涛, 等. 一种实时GNSS时间传递算法[J]. 天文学报, 2016, 57(3): 320-325 (Yu Heli, Hao Jinming, Xie Jiantao, et al. A Real-Time Algorithm of GNSS Time Transfer[J]. Acta Astronomica Sinica, 2016, 57(3): 320-325)
(  0) 0) |
| [11] |
Li W, Teunissen P, Zhang B, et al. Precise Point Positioning Using GPS and Compass Observations[C]. China Satellite Navigation Conference, 2013
(  0) 0) |
| [12] |
Chen J, Zhang Y, Yang S. Real-Time Time and Frequency Transfer Based on Network Solution[C]. IGS Workshop, 2016
(  0) 0) |
2. School of Navigation and Aerospace Engineering, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China;
3. Troops 95806 of PLA, Beijing 100076, China
 2018, Vol. 38
2018, Vol. 38

