电离层对地震预报有着重要作用^[1-2]，因此电离层电子总量(total electric contents，TEC)的预报成为近些年的研究热点。学者们提出各种预测方法^[3-7]，常见的有时间序列分析^[8-10]、神经网络^[9]、自相关分析法^[5]、灰色模型^{[7, 11]}等，但采用某一固定模型一般情况下难以满足预报精度的需求^[12]。

TEC数据具有非线性、非平稳性^[12]，如果直接使用时间序列模型进行预测，模型简单但预测精度不高；神经网络选择模型参数比较复杂，且人为干涉较多；自相关分析法没有考虑非线性，不能及时有效地反映电离层变化^[5]；灰色模型在预测领域运用非常广泛，但由于电离层TEC数据量比较大，离散程度也相应变大，其预报精度较差^[13]。汤俊^[8]提出经验模态分解(EMD)与时间序列分析法相结合来预报TEC值，但EMD的模态混叠可能造成信号分解不准确，影响预测精度。针对模态混叠，郑旭^[14]提出改进的集总平均经验模态分解(modified ensemble empirical model decomposition，MEEMD)。利用传统ARMA模型预测的主要问题是极值点预测误差较大，为此李磊^[15]提出了ARMA模型残差修正预测。本文提出一种改进的集总平均经验模态分解与自回归移动平均模型(ARMA)组合的残差修正模型，即MEEMD-ARMA残差修正模型。

1 模型原理

本文结合MEEMD分解和抑制模态混叠两方面的优势以及ARMA残差修正预报模型对极值点预测修正的优点，建立MEEMD-ARMA残差修正模型。具体步骤如下^[16]。

1) 利用MEEMD将TEC数据时间序列x(t)进行分解。

2)将所有分量用ARMA(p，q)模型^{[9, 12, 15, 17]}进行预测。设x_t(t=1, 2, …)为电离层TEC数据构成的时间序列，对于任意t, 满足：

$ \begin{array}{l} {\mathit{\boldsymbol{x}}_t} - {\varphi _1}{\mathit{\boldsymbol{x}}_{t - 1}} - {\varphi _2}{\mathit{\boldsymbol{x}}_{t - 2}} - \cdots - {\varphi _p}{\mathit{\boldsymbol{x}}_{t - p}} = \\ {\mathit{\boldsymbol{\varepsilon }}_t} - {\theta _1}{\mathit{\boldsymbol{\varepsilon }}_{t - 1}} - {\theta _2}{\mathit{\boldsymbol{\varepsilon }}_{t - 2}} - \cdots - {\theta _q}{\mathit{\boldsymbol{\varepsilon }}_{t - q}} \end{array} $

(1)

式中，x(t)由m个IMF分量和一个残余分量组成，即${{\mathit{\boldsymbol{x}}}_{t}}\xrightarrow{\rm{MEEMD}}\sum\limits_{k=1}^{m}{\left[ {{\mathit{\boldsymbol{c}}}_{k}}\left( t \right) \right]+\mathit{\boldsymbol{r}}\left( t \right);}$$\varepsilon =\{{\mathit{\boldsymbol{\varepsilon }}_{t}},t=0,\pm 1,\cdots \}$是方差为σ²的白噪声序列，{x_t}是均值为μ的ARMA(p，q)过程。

本文ARMA模型定阶采用AIC准则：

$ \begin{array}{l} {\rm{AIC}}(p, q) = \mathop {{\rm{min}}}\limits_{0 \le m, n \le L} \left( {m, n} \right) = \\ \mathop {{\rm{min}}}\limits_{0 \le m, n \le L} \left\{ {{\rm{ln}}{{\hat \sigma }^2} + \frac{{2\left( {m + n} \right)}}{N}} \right\} \end{array} $

(2)

式中，${{{\hat \sigma }^2}}$是对噪声项方差的估计，L为预先给定的最高阶数，N为已知观测数据样本容量。利用AIC准则定阶是指在p、q一定变化范围内寻求使得统计量AIC(p, q)达到最小的点(p, q)，用作(p, q)的估计^{[9, 15]}。

3) 利用式(1)对所有IMF分量和残余分量进行预报，得到预报值${{\mathit{\boldsymbol{\hat c}}}_\mathit{k}}$，则预报值与观测值的残差$\mathit{\boldsymbol{\gamma }} ={\mathit{\boldsymbol{c}}_k} - {{\mathit{\boldsymbol{\hat c}}}_\mathit{k}}$；再对残差用式(1)进行预报，得到预报值${\mathit{\boldsymbol{\hat \gamma }}}$。则修正后的预报值为：

$ {{\mathit{\boldsymbol{\tilde x}}}_t} = \mathit{\boldsymbol{\hat \gamma }} + {{\mathit{\boldsymbol{\hat x}}}_t} $

(3)

式中，${{\mathit{\boldsymbol{\tilde x}}}_t}$为预测残差修正后的TEC预测值，${{\mathit{\boldsymbol{\hat x}}}_t}$、${\mathit{\boldsymbol{\hat \gamma }}}$分别为ARMA模型预测的TEC值及其相应的预报残差值。

2 实例计算与分析 2.1 数据选取及模型评价指标

本文采用IGS提供的2 h时间分辨率的全球TEC数据对改进模型进行分析。参照文献[12]，选取2015年年积日16~45、135~164、225~254、315~344四个时段内低纬(5°N，120°W)、中纬(45°N，60°E)以及中纬(45°N，120°W)、高纬(85°N，120°W)的TEC数据进行分析，用前25 d的TEC值预测后5 d的TEC值。先对选取的数据进行MEEMD分解，得到IMF分量和残余分量，然后利用ARMA残差修正模型对各分量进行预测，将各分量预测值相加得到后5 d的预测值，利用后5 d的观测数据作预测检验。本文采用标准差σ、平均相对精度P以及平均绝对误差Δ来评定预测结果：

$ \sigma = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({{\mathit{\hat x}}_i} - {x_i})}^2}} } $

(4)

$ P = 1 - \sum\limits_{i = 1}^n {\frac{{\left| {{{\mathit{\hat x}}_i} - {x_i}} \right|}}{{{x_i}}}} $

(5)

$ \mathit{\Delta } = \frac{1}{n}\sum\limits_{{\rm{i}} = 1}^n {\left| {{{\mathit{\hat x}}_i} - {x_i}} \right|} $

(6)

其中，x_i和${{{\mathit{\hat x}}_i}}$分别为TEC的观测数据和预测数据；n为数据个数。

2.2 数据处理及分析

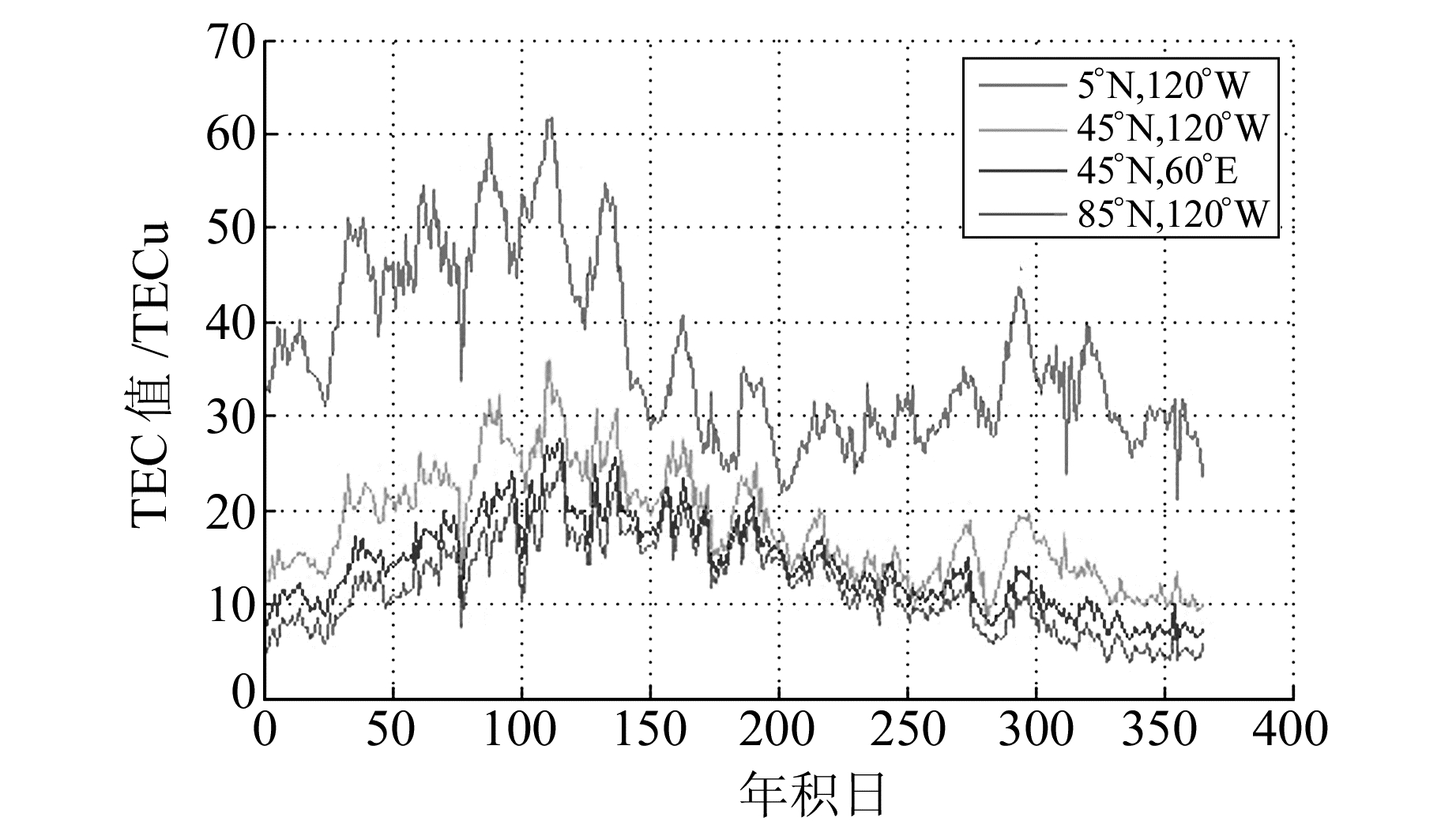
由图 1对比发现，选取的数据波动变化趋势基本一致。在低纬(5°N，120°W)，全年TEC值变化幅度较大，最大值与最小值相差40.5 TECu，而其他3个位置相对较小；在经度一定时，TEC值随纬度增大而减小，与文献[12]结论一致，且各年积日低纬TEC日均值明显比中高纬大；在中纬(45°N，60°E)和(45°N，120°W)两个位置，TEC值有一定差异，但差值跨度不大。

本文选取中纬(45°N，120°W)年积日135~164的TEC数据进行具体分析。先进行MEEMD及EMD分解，而两种方法均通过筛分过程将信号分解成一系列特征尺度由最小到最大依次增大的IMF和一个残余分量。从图 2可知，EMD分解将原始数据分解成6个本征模态和1个残余分量，而MEEMD分解将原始数据分解成7个本征模态和1个残余分量。从分解效果看，MEEMD分解比EMD分解多1个本征模态，分解频率尺度更加精细；而两种分解方法前3个高频分量可以反映出，EMD分解模态混叠现象比MEEMD分解更加明显，表明MEEMD分解能有效抑制模态混叠。

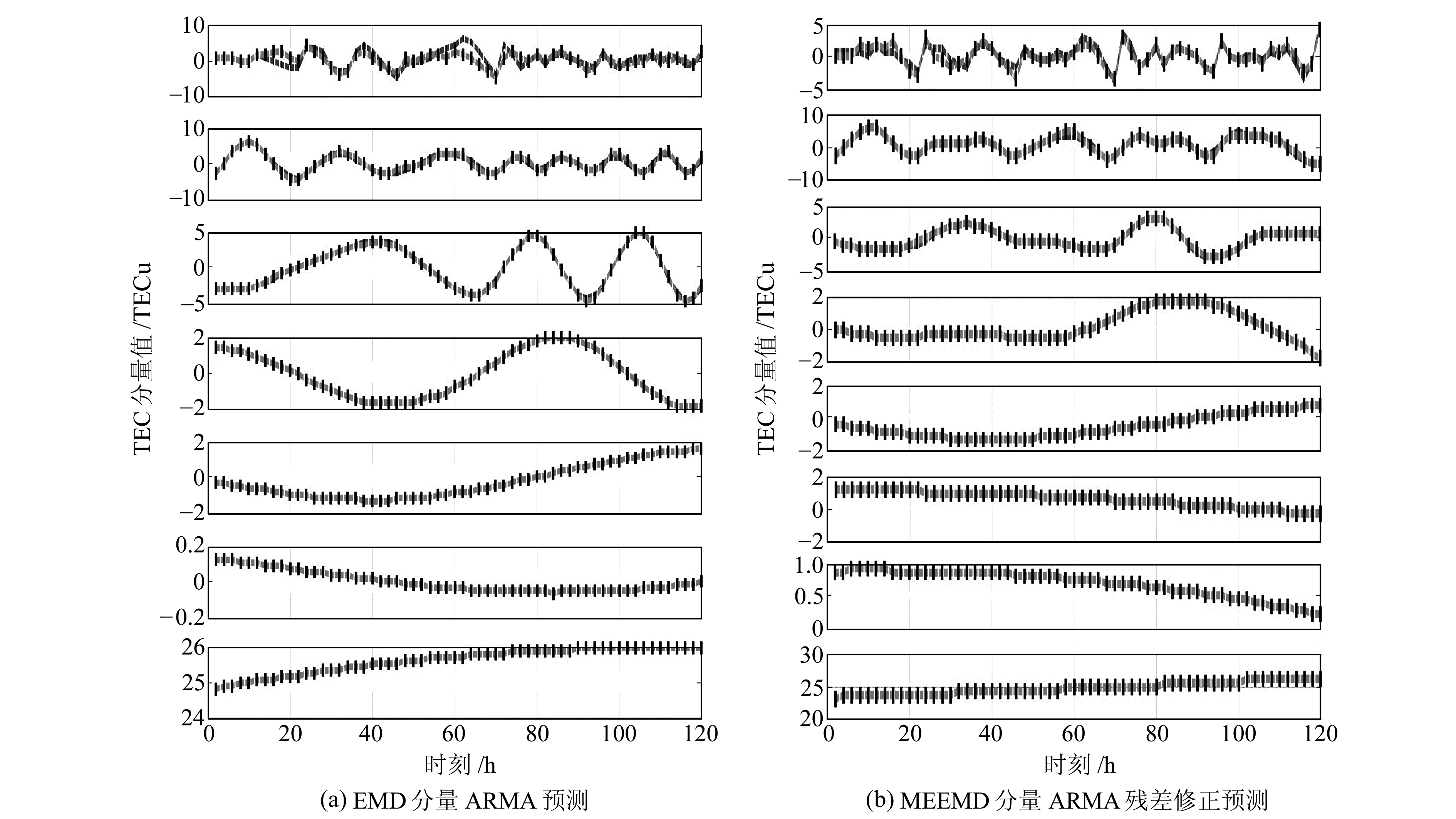
分别利用ARMA预测模型和ARMA残差修正预测模型对EMD分量和MEEMD分量进行预测(见图 3，浅色为分量预测值，深色为原始分量)。可以看出，图 3(a)第一个分量预测值与实际值的符合程度明显比图 3(b)第一个分量预测值与实际值的符合程度差，其他分量的符合程度基本相当。从整体考虑，利用MEEMD-ARMA残差修正模型的预测精度比EMD-ARMA模型预测精度高。

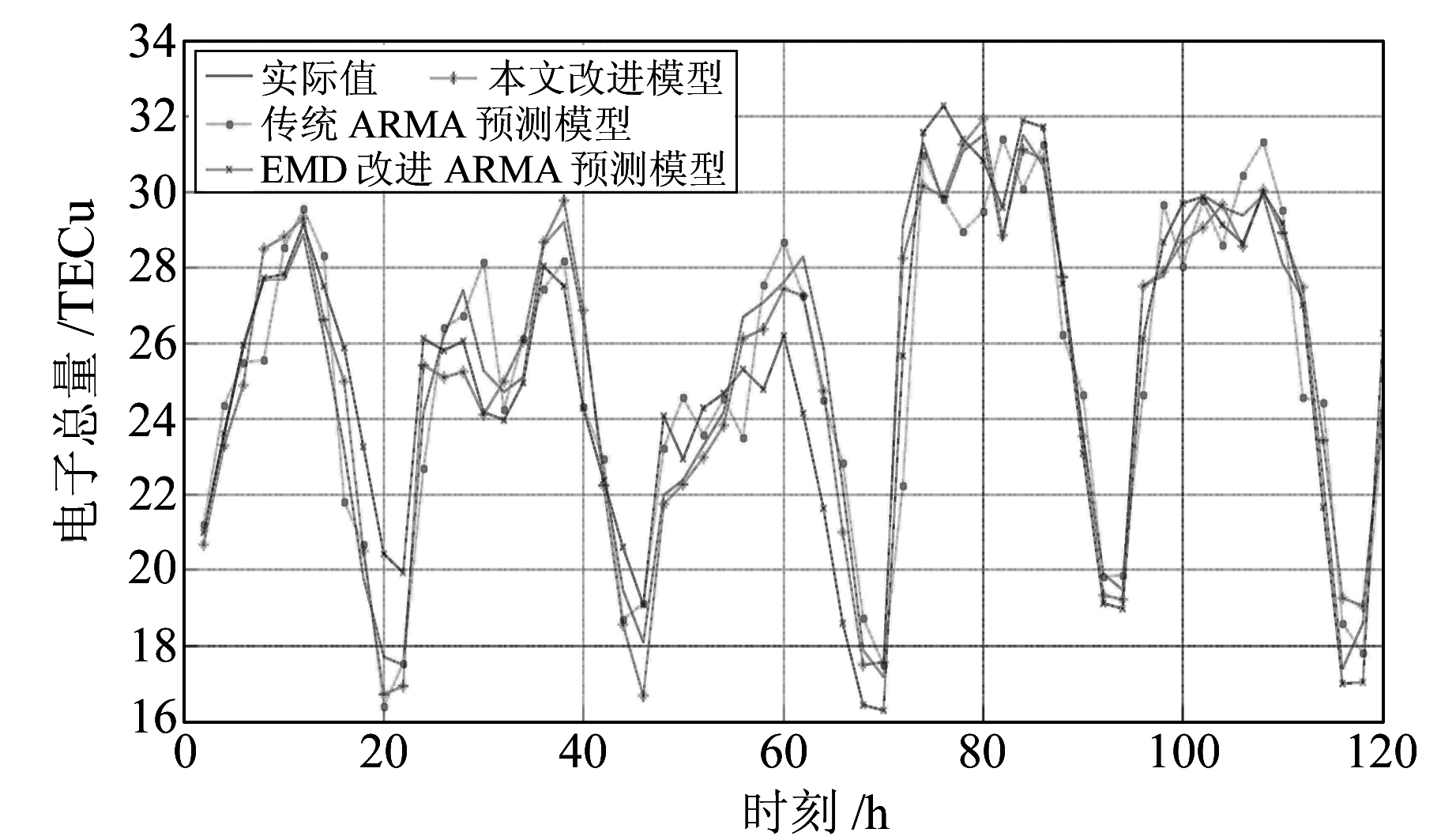
以中纬(45°N，120°W)年积日135~159的TEC数据为训练数据，分别用传统的ARMA模型、EMD-ARMA组合模型以及MEEMD-ARMA残差修正组合模型对数据进行拟合，利用最小二乘法计算拟合参数，再对160~164年积日内60个TEC数据进行预测。从图 4可以看出，传统ARMA预测模型和EMD-ARMA组合模型在极点附近历元的预测效果普遍不好，而本文的MEEMD-ARMA残差修正组合模型在EMD-ARMA组合模型的基础上得到进一步优化，与实际值符合较好。还可以看出，电离层TEC值在每天UT22：00左右达到最低值，UT12:00达到最高值，而在这些极点附近，MEEMD-ARMA残差修正组合模型与实际值的符合程度普遍比其他两种模型要好。

表 1、表 2分别给出相同经纬度、不同时段以及相同时段、不同经纬度5个年积日的平均预测误差结果。从表 1可以看出，同一位置、不同时段，改进模型的预测精度普遍高于原有的两种模型，各指标随选取时段的变化而变化，其中在TEC值相对稳定的时段精度更高。对比表 2，在同一时段、同一经度标准差随纬度的增加而减小，相对精度随纬度的增加呈现升高趋势；而相同时刻、相同纬度、不同经度预测精度也有变化，标准差的差异比较明显，而平均绝对误差却比较接近，这在一定程度上验证了文献[12]的结论。表 3数据同样验证了改进模型的预测精度比原有两种模型高。

对电离层TEC值影响较大的因素主要有地磁活动及K_p太阳活动(F_10.7)。图 5给出4个时段的K_p指数和F_10.7指数。16~45段F_10.7指数为116~167，太阳辐射较为强烈，K_p指数均小于4，说明该时段太阳活动较少，属于磁宁静；135~ 164段F_10.7指数为94~145，而在145~151段F_10.7指数低于100，K_p指数仅在159年积日超过4，其他时间均小于3，而年积日159的F_10.7指数与前后几天基本持平，说明该时段太阳活动并不活跃；231~241段F_10.7指数超过100但小于137，225~230及242~254段F_10.7指数均小于100，K_p指数在年积日228、239、240、250、254均超过4，有弱磁暴，而在年积日252，K_p指数超过5，有中等磁暴，说明该段太阳活动较多；315~344段F_10.7指数为91~120，K_p指数均小于4，说明该段太阳活动较少。由图 5可知，16~45段及315~344段F_10.7指数相对稳定，而135~164段及225~254段波动相对明显，但4个阶段的观测段与预测段太阳活动差异并不是很大。

为验证改进模型抵抗太阳活动和地磁活动影响的能力，选取年积日16~45的中纬(45°N，120°W)和年积日225~254的中纬(45°N，120°W)的TEC预测数据进行分析。对第42~44年积日内TEC值进行预测，分析3种模型在这3个年积日内预测值的评价指标以及平均绝对误差范围的百分比统计。由表 4可知，3种模型的平均绝对误差Δ均小于2 TECu，而|Δ＜|1时，改进模型的平均绝对误差百分比为94%，EMD-ARMA模型及ARMA模型分别为86%、81%；平均绝对误差在1≤Δ＜2范围时，改进模型的平均绝对误差百分比为6%，EMD-ARMA模型及ARMA模型分别为14%、19%。改进模型、EMD-ARMA模型以及ARMA模型的标准差分别为0.55、0.67、0.71，而相对精度分别为0.95、0.94、0.93。

分析3种模型在年积日252~254内预测值的评价指标以及平均绝对误差范围的百分比统计。对比表 5数据，从3项评价指标看，改进模型的预测精度比ARMA模型及EMD-ARMA模型都高。就平均绝对误差|Δ|而言，改进模型平均绝对误差|Δ|＜1时的百分比为86%，ARMA模型、EMD-ARMA模型分别为61%、70%；平均绝对误差在1≤|Δ|＜2时，改进模型、ARMA模型、EMD-ARMA模型的百分比分别是11%、31%、25%；平均绝对误差范围为2≤|Δ|＜3时，改进模型、ARMA模型、EMD-ARMA模型的百分比分别是3%、3%、5%；而平均绝对误差|Δ|≥3时，改进模型以及EMD-ARMA模型百分比均为0。显然，在太阳活动和地磁活动比较活跃时，改进模型的预测效果也比原有两种模型的预测效果好。对比表 4、表 5可知，就3种预测模型的各项指标而言，太阳活动及地磁活动水平较低的16~45段比太阳活动及地磁活动水平相对高的225~254段更为理想。就单个预测模型来看，本文改进模型在太阳活动及地磁活动水平高低时预测精度表现出的差异并不大，而另外两个预测模型表现出的差异较大，这表明改进预测模型抵抗太阳活动及地磁活动影响的能力较强。

3 结语

1) 通过对比本文模型与EMD-ARMA模型的预测值以及两种分解模型的效果，改进模型比EMD-ARMA模型的预测精度高，对于模态混叠情况有所改善。

2) 本文提出的方法对于非线性、不平稳信号处理的自适应性更强，效果更好。另外，对残差进行修正，从而提高了预测精度。

3) 通过对比不同太阳活动及地磁活动预测结果表明，改进模型TEC值预测抵抗太阳活动和地磁活动影响的能力比原有两种模型强。

本文提出的模型优于另外两种模型，但在利用ARMA模型预测时，难以确定阶数；虽然MEEMD分解相对EMD分解而言，很大程度上抑制了模态混叠，但本文并未考虑端点效应；且电离层数据影响因素复杂，这决定了TEC值准确预测模型建立十分困难。本文改进模型虽提高了预测精度，但限于预测模型的局限性以及分解中并未考虑端点效应，接下来的研究中仍有较多改进，如分解分量时同时考虑模态混叠和端点效应，并结合像神经网络等非线性预测模型进行组合预测。

致谢 感谢IGS组织提供电离层格网数据和NOAA提供太阳活动指数及地磁活动指数。