2. 中南大学地球科学与信息物理学院, 长沙市麓山南路932号, 410083
高频大地电磁法(HMT)是根据近地表工程地质勘察需求提出来的[1]。但实际工作中,复杂的地形条件对HMT的勘探效果产生严重影响,如果不考虑起伏地形对HMT数据的响应特性,将会对其资料分析带来显著误差。国内外学者针对起伏地形下传统的大地电磁法(MT)的响应特性开展研究,如Wanamaker等[2]模拟了山脊、山谷等纯地形,针对测点不同位置对结果的影响进行对比分析;Yang等[3]对比分析了不同高度的山脊、地堑等经典地形下MT的响应,得出地形影响随高度变化的规律;陈小斌等[4]提出复杂地表条件下的MT有限元格式和视电阻率定义,对斜坡型台阶和悬崖型台阶两种地形进行数值模拟,得出TM模式比TE模式更容易受地形影响的结论。尽管国内外已对起伏地形条件下MT的数值模拟作了大量研究[5-8],但研究频段均在10-3~103Hz,缺乏对高频段103~105 Hz下大地电磁法的地形影响的研究。本文采用自适应有限元方法正演模拟起伏地形,分析地垒、地堑等典型地形对10 Hz~100 kHz范围内HMT资料的影响规律,为后续通过HMT资料进行地形校正及地质解释提供必要的依据。
1 高频大地电磁二维正演基本理论当平面电磁波以任意角度入射地面时,地下介质中的电磁波总以平面波的形式,几乎垂直于大地向下传播。将Maxwell方程组按分量展开,并考虑到沿走向∂/∂z=0,得出的TE和TM模式应满足偏微分方程[1]:
| $ \frac{\partial }{\partial x}(\frac{1}{\text{i}\omega \mu }\frac{\partial {{E}_{z}}}{\partial x})+\frac{\partial }{\partial y}(\frac{1}{\text{i}\omega \mu }\frac{\partial {{E}_{z}}}{\partial y})+\sigma {{E}_{z}}=0 $ | (1) |
| $ \frac{\partial }{\partial x}(\frac{1}{\sigma }\frac{\partial {{H}_{z}}}{\partial x})+\frac{\partial }{\partial y}(\frac{1}{\sigma }\frac{\partial {{H}_{z}}}{\partial y})+\text{i}\omega \mu {{H}_{z}}=0 $ | (2) |
式(1)、(2)可表示为:
| $ \nabla \left( \tau \nabla u \right)+\lambda u=0 $ | (3) |
其中,∇为二维哈密顿算子。对E型波:u=Ez,
结合内、外边界条件, 正演的边值问题可以表示为:
| $ \left. \begin{align} & \nabla \left( \tau \nabla u \right)+\lambda u=0\ \ \ \ \ \in \mathit{\Omega } \\ & u=1\ \ \ \ \ \ \in AB \\ & \frac{\partial u}{\partial n}=0\ \ \ \ \in AD, BC \\ & \frac{\partial u}{\partial n}+ku=0\ \ \ \ \in CD \\ & {{u}_{1}}={{u}_{2}}\ \ \ \ \in {{\mathit{\Gamma }}_{1}} \\ & {{\tau }_{1}}\frac{\partial {{u}_{1}}}{\partial n}={{\tau }_{2}}\frac{\partial {{u}_{2}}}{\partial n}\ \ \ \ \in {{\mathit{\Gamma }}_{1}} \\ \end{align} \right\} $ | (4) |
倘若在区域内仅有一个不均匀体存在, 利用广义变分原理构造泛函[2-4]:
| $ \begin{align} & I\left( u \right)={{\int }_{\mathit{\Omega }}}\left[\frac{1}{2}\tau {{\left( \nabla u \right)}^{2}}-\frac{1}{2}\lambda {{u}^{2}} \right]\text{d}\mathit{\Omega }= \\ & {{\int }_{{{\mathit{\Omega }}_{1}}}}\left[\frac{1}{2}{{\tau }_{1}}{{(\nabla {{u}_{1}})}^{2}}-\frac{1}{2}{{\lambda }_{1}}u_{_{1}}^{^{2}} \right]\text{d}\mathit{\Omega }+ \\ & {{\int }_{{{\mathit{\Omega }}_{2}}}}\left[\frac{1}{2}{{\tau }_{2}}{{(\nabla {{u}_{2}})}^{2}}-\frac{1}{2}{{\lambda }_{2}}u_{_{2}}^{^{2}} \right]\text{d}\mathit{\Omega } \\ \end{align} $ | (5) |
代入边界条件, 二维大地电磁边值问题式(4)与下列变分问题等价:
| $ \left. \begin{align} & F\left( u \right)={{\int }_{\mathit{\Omega }}}\left[\frac{1}{2}\tau {{\left( \nabla u \right)}^{2}}-\frac{1}{2}\lambda {{u}^{2}}\text{d} \right]\mathit{\Omega }+ \\ & {{\int }_{CD}}\frac{1}{2}\tau k{{u}^{2}}\text{d}\mathit{\Gamma } \\ & u{{|}_{AB}}=1, \delta F\left( u \right)=0 \\ \end{align} \right\} $ | (6) |
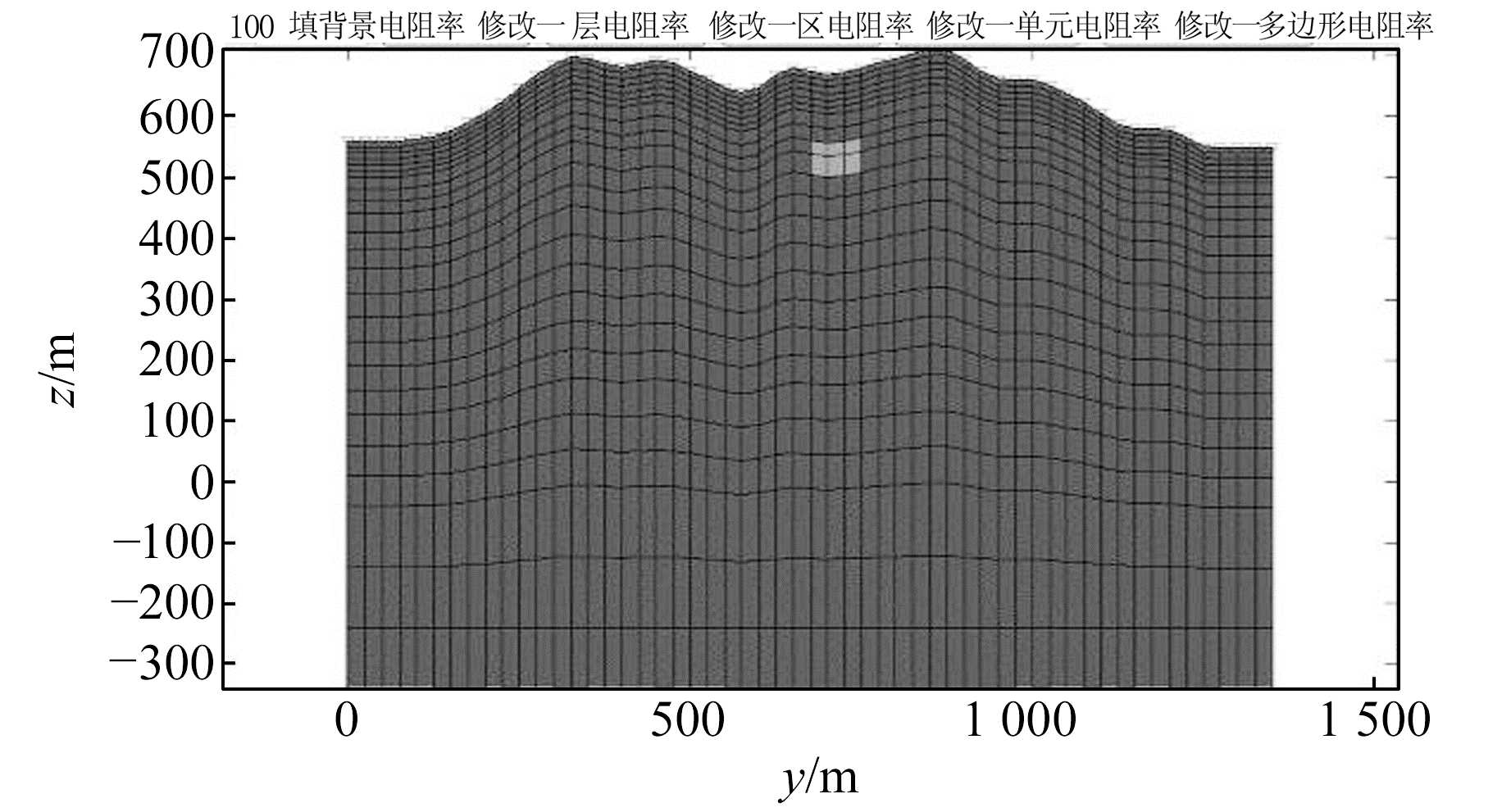
基于电磁法正演基本理论,在Matlab平台上编制二维HMT自适应地形建模软件,软件功能主要包括任意地形建模、填充电阻率、大地电磁正演功能(图 1)。
|
图 1 二维大地电磁自适应地形建模软件 Fig. 1 Adaptive terrain forward modeling of magnetotelluric |
结合EH-4电导率成像系统的参数设置,频率选取与之保持一致,选用的频点为10 Hz~100 kHz,共41个频点。
二维情况下单元网格剖分如下。x轴网格扩展宽度(单位m):80 000,25 000,10 000,4 000,1 500,500;测点点距:25 m。z轴网格宽度(单位m):40 000,16 000,8 000,2 000,500,200,50,10,10,10,10,10,10,20,20,20,30,30,30,40,40,40,40,40,40,50,50,50,100,100,100,2 500,4 000,5 000,10 000,20 000,50 000,100 000;空气网格宽度(单位m):40 000,16 000,8 000,2 000,500,200,50;底部扩边网格(单位m):2 500,4 000,5 000,10 000,20 000,50 000,100 000。
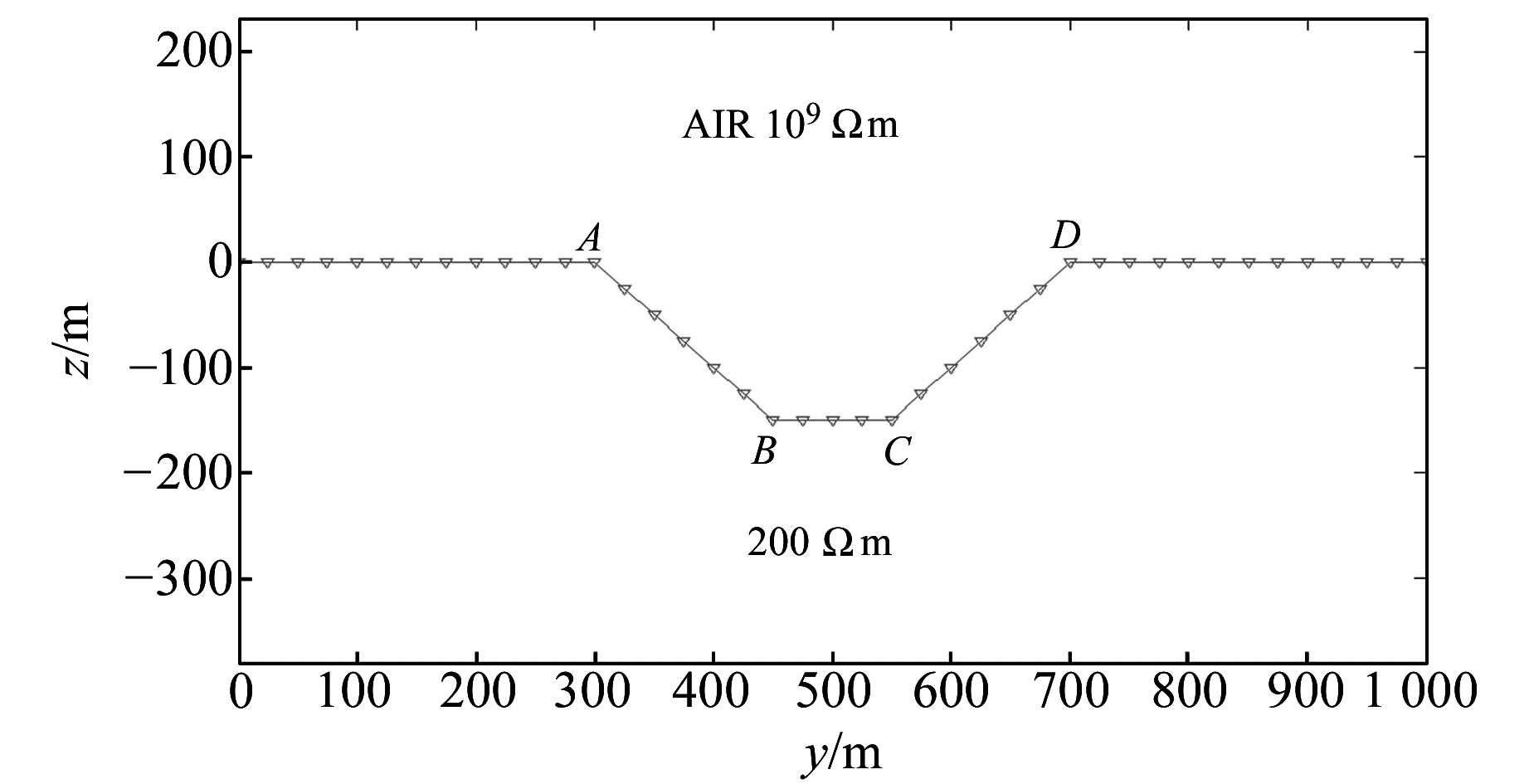
3 地形影响规律分析 3.1 地堑模型设计的地堑地形模型如图 2所示,研究区域是电阻率为200 Ωm的均匀半空间,地堑模型上部宽度400 m,下部宽度100 m,高差150 m。
|
图 2 地堑模型 Fig. 2 The valley model |
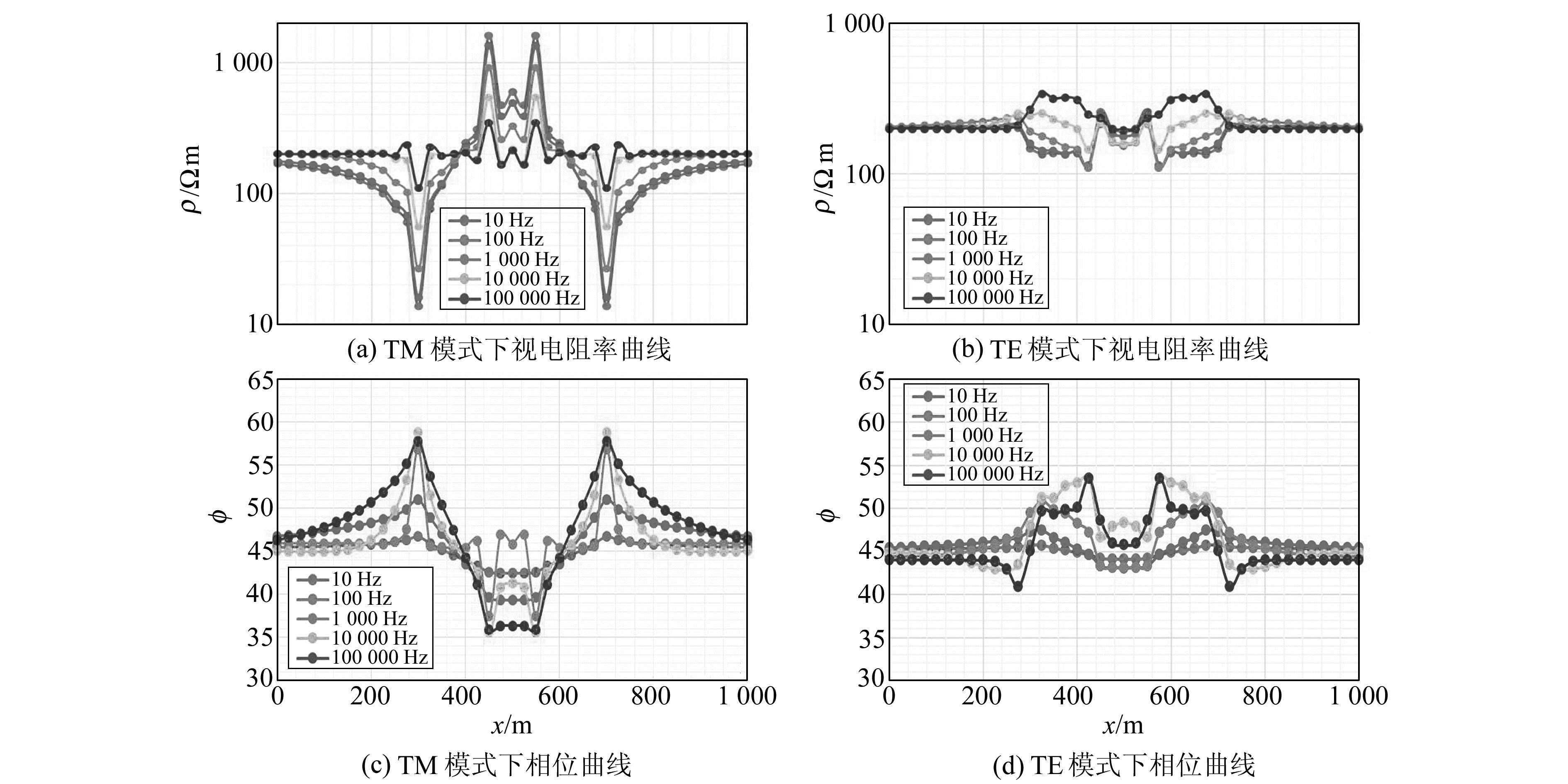
图 3分别给出地堑地形模型下不同测点位置与不同频率的模拟计算结果。分析地堑地形模型下的HMT响应,可以得出如下规律。
|
图 3 地堑模型HMT响应曲线 Fig. 3 HMT response curve of the valley model |
1) 地堑地形不论对TM模式还是TE模式均有影响,但对TM模式的影响比TE要严重。
2) 地堑地形对TM模式的响应特征:视电阻率曲线在A、D两点出现极小值,B、C两点出现极大值;高频段影响小,低频段影响大。相位曲线与视电阻率曲线规律相反,在A、D两点出现极大值,B、C两点出现极小值。
3) 地堑地形对TE模式的响应特征:视电阻率曲线在A、D两点出现相对极大值,B、C两点出现相对极小值;高频段影响大,低频段影响小。相位曲线规律与视电阻率曲线类似。
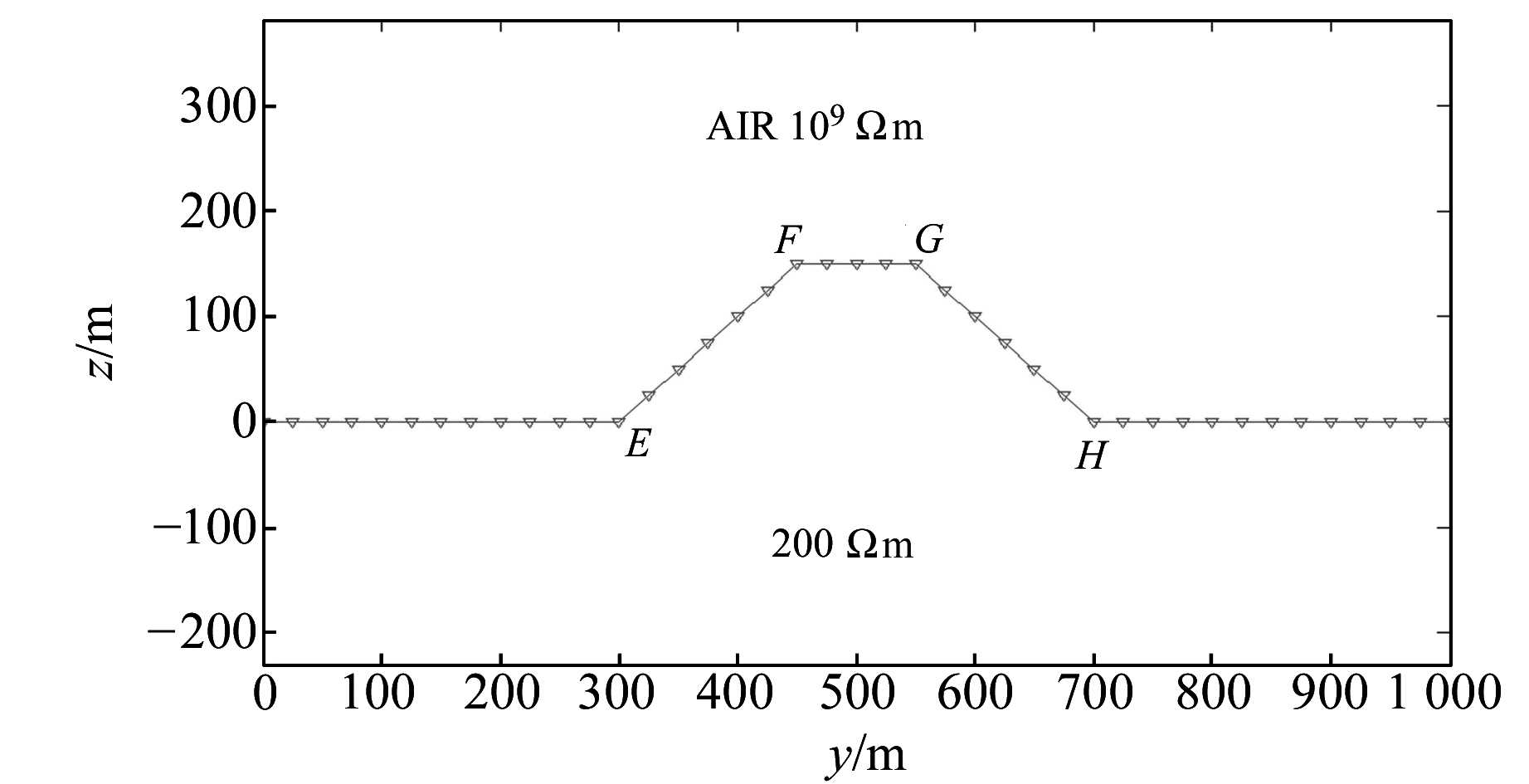
3.2 地垒模型设计的地垒地形模型如图 4所示,研究区域是电阻率为200 Ωm的均匀半空间,地垒模型上部宽度100 m、下部宽度400 m,高差为150 m。图 5分别给出地垒地形模型下不同测点位置与不同频率的模拟计算结果。分析地垒地形模型下的HMT响应,可以得出以下规律。
|
图 4 山峰模型 Fig. 4 The peak model |

|
图 5 地垒模型HMT响应曲线 Fig. 5 HMT response curve of the peak model |
1) 地垒地形不论对TM模式还是TE模式均有影响,但对TM模式的影响比TE要严重。
2) 地垒地形对TM模式的响应特征:视电阻率曲线在E、H两点出现极大值,F、G两点出现极小值;高频段影响小,低频段影响大。相位曲线与视电阻率曲线规律相反,在E、H两点出现极小值,F、G两点出现极大值。
3) 地垒地形对TE模式的响应特征:视电阻率曲线在E、H两点出现相对极小值;F、G两点出现相对极大值;高频段影响大,低频段影响小。相位曲线规律与视电阻率曲线类似。
3.3 任意起伏地形模型任意地形模型如图 6所示,地形起伏不平,最大高差约200 m,研究区域是电阻率为1 000 Ωm的均匀半空间。图 7为正演模拟所得的HMT响应拟断面图,图 7(a)为TM模式下视电阻率和阻抗相位断面图,其中纵坐标为频率(取对数),横坐标为模型测点里程;图 7(b)为TE模式下视电阻率和阻抗相位断面图。从正演模拟结果可以看出,山脊和山谷位置的HMT响应特征与地垒、地堑相符。另外,可得出以下规律。
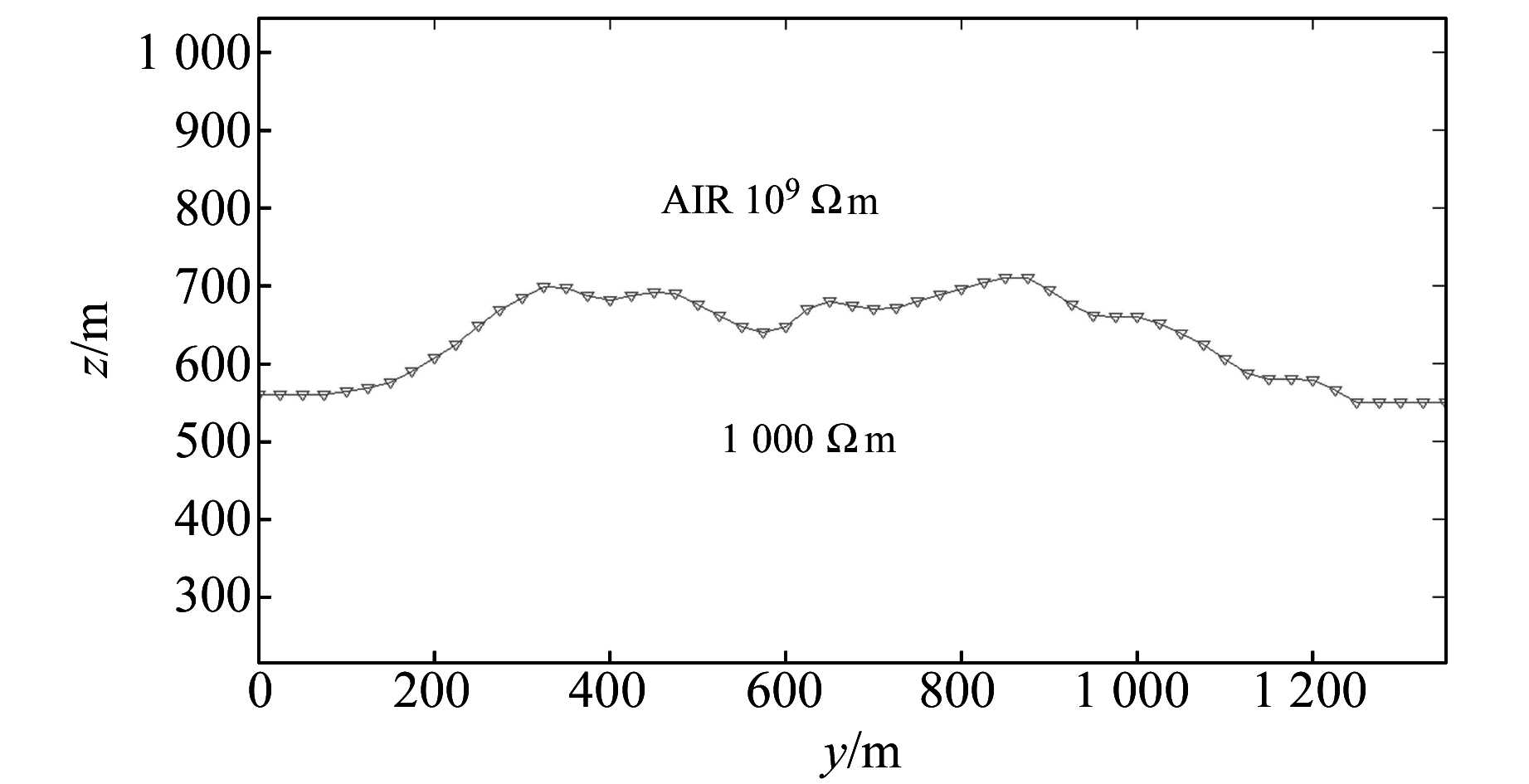
|
图 6 任意地形模型 Fig. 6 The rolling terrain model |
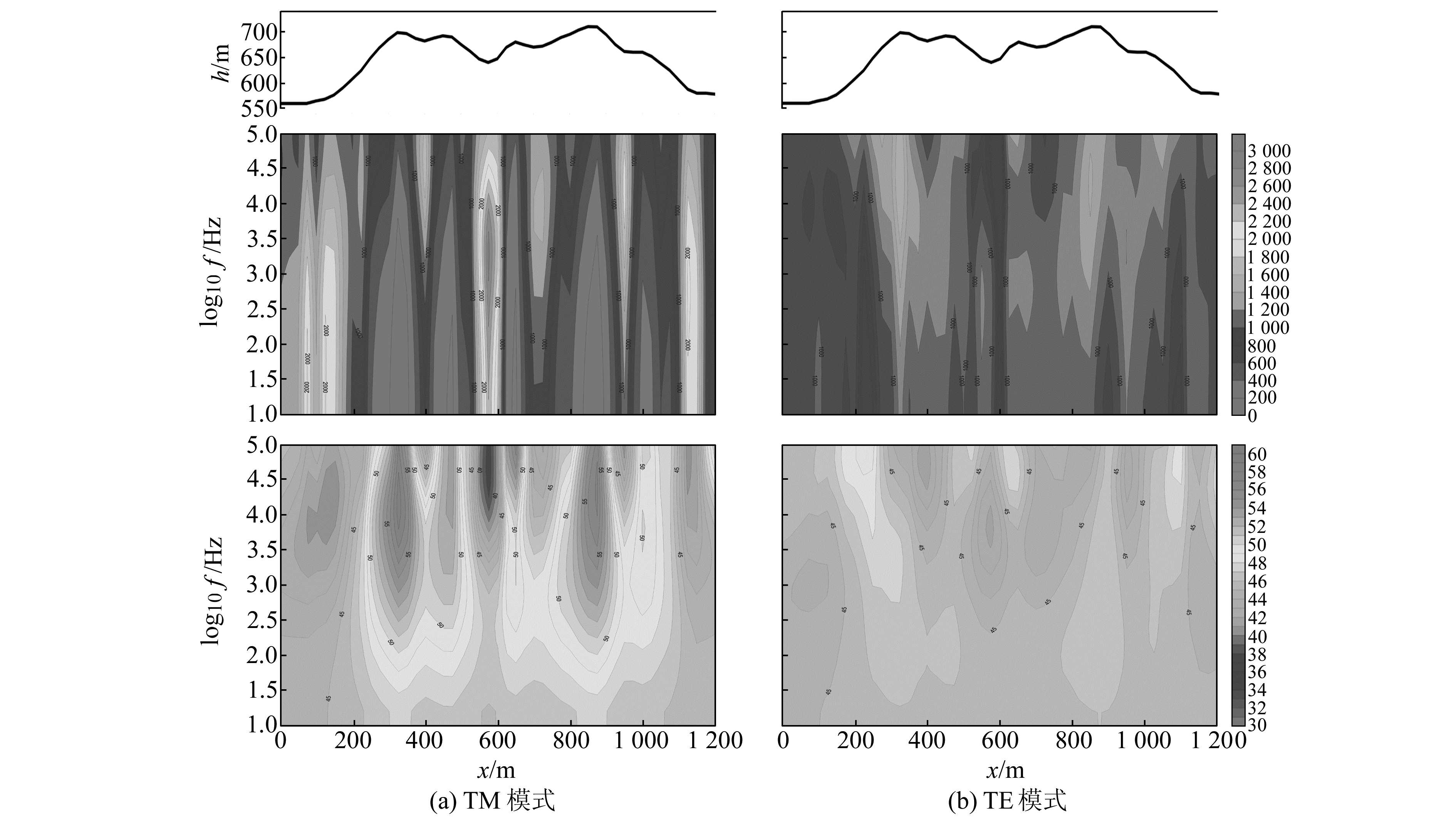
|
图 7 任意起伏地形HMT响应曲线 Fig. 7 HMT response curve of rolling terrain model |
1) 起伏地形对二维地电模型的HMT响应都有影响,视电阻率所受地形影响比阻抗相位资料更为强烈。
2) 起伏地形对TE和TM极化模式资料都有影响,其中TM极化模式的视电阻率资料所受影响远比其他资料大得多。
3) 在TM极化模式中,低频部分的视电阻率比高频部分更容易受起伏地形的影响。而在TE极化模式中,高频部分的视电阻率比低频部分更容易受起伏地形的影响。
4) 山脊地形的影响范围比山谷地形大,为降低地形影响,测点位置应尽量避开山脊或山峰,最好选在宽阔的山谷。
4 结语本文通过有限元数值模拟,对典型地堑、地垒、任意起伏地形的数值模拟结果进行分析,得出起伏地形条件下高频大地电磁法的响应特征,所揭示的规律具有普适性,可为山区高频大地电磁勘探外业布置与数据分析解释提供参考。
| [1] |
王烨, 曹哲明, 汤井田. 铁路隧道工程勘察中高频大地电磁测深应用效果研究[J]. 工程地质学报, 2005, 13(3): 424-428 (Wang Ye, Cao Zheming, Tang Jingtian. Application of the High Frequency Magnetotellurics Sounding in the Exploratory Investigation of Railway Tunnel Engineering[J]. Journal of Engineering Geology, 2005, 13(3): 424-428)
(  0) 0) |
| [2] |
Wannamaker P E. Two-Dimensional Topographic Response in Magnetotellurics Modeled Using Finite Element[J]. Geophysics, 1986, 51(11): 2131-2144 DOI:10.1190/1.1442065
(  0) 0) |
| [3] |
Yang C H, Tseng H W. Topographic Responses in Magnetometric Resistivity Modeling[J]. Geophysics, 1992, 57(10): 1409-1418
(  0) 0) |
| [4] |
陈小斌. MT二维正演计算中地形影响的研究[J]. 石油物探, 2000, 39(3): 65-71 (Chen Xiaobin. On the Research of the Influence of Terrain to MT 2D Forward Computation[J]. Geophysical Prospecting for Petroleum, 2000, 39(3): 65-71)
(  0) 0) |
| [5] |
汤井田, 任政勇, 化希瑞. 地球物理学中的电磁场正演与反演[J]. 地球物理学进展, 2007, 22(4): 1181-1194 (Tang Jingtian, Ren Zhengyong, Hua Xirui. The Forward Modeling and Inversion in Geophysical Electromagnetic Field[J]. Progress in Geophysics, 2007, 22(4): 1181-1194)
(  0) 0) |
| [6] |
王绪本, 李永年, 高永才. 大地电磁测深二维地形影响及其校正方法研究[J]. 物探化探计算技术, 1999, 21(4): 327-332 (Wang Xuben, Li Yongnian, Gao Yongcai. Two Dimensional Topographic Responses in Magnetotellric Sound and Its Correction Methods[J]. Computing Techniques for Geophysics and Geochemical Exploration, 1999, 21(4): 327-332)
(  0) 0) |
| [7] |
陈小斌, 张翔, 胡文宝. 有限元直接迭代算法在MT二维正演计算中应用[J]. 石油地球物理勘探, 2000, 35(4): 487-496 (Chen Xiaobin, Zhang Xiang, Hu Wenbao. Application of Finite-Element Direct Iteration Algorithm to MT 2-D Forward Computation[J]. Oil Geophysical Prospecting, 2000, 35(4): 487-496)
(  0) 0) |
| [8] |
赵广茂, 李桐林, 王大勇, 等. 基于二次场二维起伏地形MT有限元数值模拟[J]. 吉林大学学报:地球科学版, 2008, 35(6): 1055-1059 (Zhao Guangmao, Li Tonglin, Wang Dayong, et al. Secondary Field-Based Two Dimensional Topographic Numerical Simulation in Magnetotellurics by Finite Element Method[J]. Journal of Jilin University:Earth Science Edition, 2008, 35(6): 1055-1059)
(  0) 0) |
2. School of Geosciences an Info-Physics, Central South University, 932 South-Lushan Road, Changsha 410083, China
 2018, Vol. 38
2018, Vol. 38

