近20 a来,卫星测高技术日趋成熟,极大地推动了海洋潮汐研究,特别是1992年TOPEX/Poseidon(T/P)卫星发射以来,许多学者利用这种高质量的数据研制发布了全球海潮模型[1]。然而T/P卫星地面轨迹相对稀疏,相邻平行轨迹在赤道上的经度差达到2.83°[2],使得基于T/P数据的海潮模型在局部近海地区准确度不佳。ERS-2与后续卫星Envisat(ERS系列卫星)弥补了T/P卫星空间分辨率的不足,其相邻平行轨迹在赤道上的经度差仅为0.7°,空间分辨率优于1°×1°。但受限于太阳同步轨道以及35 d的重复周期,利用潮汐调和分析方法不能从中准确分离出S2等太阳分潮,如何利用这些资料提取潮汐信息有待进一步研究。Anderson[3]以及Shepherd等[4]相继基于ERS卫星测高数据,采用正交响应分析提取了北大西洋海域和南极George Ⅵ冰架附近的海域潮汐信息。Ray[5]建议使用数据同化的方法将ERS系列测高数据与动力学模式结合起来,以克服太阳同步采样的限制。目前,ERS-1/2、Envisat-1系列卫星积累了超过10 a的连续观测资料,本文选取中国海及其邻近西太平洋海域作为研究区域,探讨ERS卫星35 d重复周期下潮汐的混叠现象,利用ERS系列卫星的海面高观测时间序列进行正交响应分析以提取潮汐调和常数,并给出初步研究成果。
1 ERS系列测高卫星的潮汐混叠及正交响应分析 1.1 潮汐混叠执行精密重复轨道任务的测高卫星为我们在开阔海域提供了良好的星下点观测时间序列,然而测高卫星受重复周期轨道的限制,对某一点的采样间隔ΔT一般为数d或者数10 d,远大于作为潮汐主体的半日分潮和全日分潮,从而导致信号彼此重叠失真的混叠现象,潮汐信号将混叠到频率低于1/2ΔT的频率上[6-7]。表 1(单位d)给出了ERS-2(Envisat-1)卫星12个主要分潮的混叠周期,包括主要半日分潮(M2、S2、N2、K2)、全日分潮(O1、P1、K1、Q1)和长周期分潮(Mf、Mm、Ssa、Sa),表中对角线元素是各分潮的混叠周期,非对角线元素是对应两个分潮的会合周期,即分辨两个频率分潮所需要的最短时间[8]。
|
|
表 1 主要分潮混叠周期与汇合周期 Tab. 1 Alias periods (diagonal) and alias synodic period (off diagonal) |
在太阳同步轨道下,一个交点日等于一个平太阳日,ERS-2和Envisat-1的35 d重复周期正好是S2分潮周期的70倍,这样在某一固定星下点,测高卫星在每一个周期获得的S2分潮相位相同,S2分潮变成一个常数。在该采样规律下,利用传统调和分析方法分离M2和N2分潮需要大约9 a的连续观测,分离K1、P1与周年分潮Sa需要20 000 a以上。同样地,K2的混叠周期和Ssa也难以分离。本文采用了正交响应分析方法,这种方式依据导纳函数的平滑性推算各潮族中的分潮信息,不需要事先指定分潮,避免了单个分潮之间的相角比较,对于从ERS系列卫星数据中提取S2分潮有相当的优势。
1.2 正交响应分析潮汐响应分析是Munk等[9]提出的一种潮汐谱分析方法。它把海洋作为一个物理响应系统,通过一个响应权函数把平衡潮和实际潮位联系起来,将某点在时刻t的潮高表示成一种卷积的形式:
| $ \begin{matrix} \zeta \left( \lambda, \theta, t \right)=\sum\limits_{n=2}^{3}{\sum\limits_{m=0}^{n}{\sum\limits_{s=-S}^{S}{{}}}} \\ [a_{_{n}}^{^{m}}(t-s\Delta T)U_{_{n}}^{^{m}}\left( \lambda, \theta, s \right)+b_n^m(t-s\Delta T)V_{_{n}}^{^{m}}\left( \lambda, \theta, s \right)] \\ \end{matrix} $ | (1) |
式中,a和b是引潮位随时间变化的部分,可以写成a+ib的复数形式,由月球和太阳位置所决定;s是一个小整数,s=0,±1,±2,±3;ΔT为时间间隔;U和V是随位置变化的待求权函数。
Groves等[10]指出,推算潮汐的时间项a和b不正交,建议利用导纳函数固有的平滑度和正交性,以时间项组合的正交函数来代替原来的时间项。在只考虑半日分潮、全日分潮以及主要项n=2的情况下,正交响应分析中的潮高可表示成:
| $ \zeta \left( t \right)=\sum\limits_{m=1}^{2}{\sum\limits_{j=0}^{2S}{[U_{_{j}}^{^{m}}\left( \lambda, \theta \right)P_{_{j}}^{^{m}}\left( t \right)+V_{_{j}}^{^{m}}\left( \lambda, \theta \right)Q_{_{j}}^{^{m}}\left( t \right)]}} $ | (2) |
式中,P和Q是引潮位中时间函数a和b的线性组合。一般情况下,正交潮展开为3项(j=0,1,2),s=1,已经足够解释大多数潮位变化[11]。在实际展开中,这种正交展开式是根据各潮族进行的,即针对每一个潮族给出一组正交权。具体正交权系数以及正交潮参数与调和常数的转换关系见文献[12]。
本文选取表 1中12个分潮Ssa、Sa、Mf、Mm、M2、S2、N2、K2、O1、P1、K1、Q进行计算,采用如下潮高观测方程:
| $ \begin{align} &\zeta \left( t \right)={{h}_{0}}+a(t-{{t}_{0}})+ \\ &\sum\limits_{m=1}^{2}{\sum\limits_{j=0}^{2s}{{}}}[U_{_{j}}^{^{m}}\left( \lambda, \theta \right)P_{_{j}}^{^{m}}\left( t \right)+V_{_{j}}^{^{m}}\left( \lambda, \theta \right)Q_{_{j}}^{^{m}}\left( t \right)]+ \\ &\sum\limits_{i=1}^{4}{{{f}_{i}}}{{C}_{i}}\left( \lambda, \varphi \right)\text{cos}[{{\sigma }_{i}}t+{{({{V}_{0}}+U)}_{i}}]+ \\ &\sum\limits_{i=1}^{4}{{{f}_{i}}}{{S}_{i}}\left( \lambda, \varphi \right)\text{sin}[{{\sigma }_{i}}t+{{({{V}_{0}}+U)}_{i}}] \\ \end{align} $ | (3) |
式中,h0是平均海面,a为海面变化的长期趋势,t0为参考初始时间,σ为分潮角速度;C与S为4个长周期分潮Sa、Ssa、Mf、Mm的调和常数余弦分量和正弦分量,与U和V一起构成方程的待求参数。
2 数据处理本文研究海域包括中国海和西太平洋(0°~50°N,100°~150°E),采用ERS-2卫星1~84周期OPR数据与Envisat-1卫星9~93周期GDR数据,时间跨度为1995-05~2010-10。对这两颗卫星的数据分别进行预处理,包括对流层干湿改正、电离层改正、海况偏差改正、逆气压改正、固体潮改正、海潮负荷改正和极潮改正,具体改正模型如表 2所示,具体编辑准则见文献[13-14]。将预处理后的数据统一到Topex椭球,并采用共线平差处理,构建统一的沿轨海面高观测时间序列[15]。
|
|
表 2 卫星测高数据处理改正模型 Tab. 2 Satellite altimetry data processing correction models |
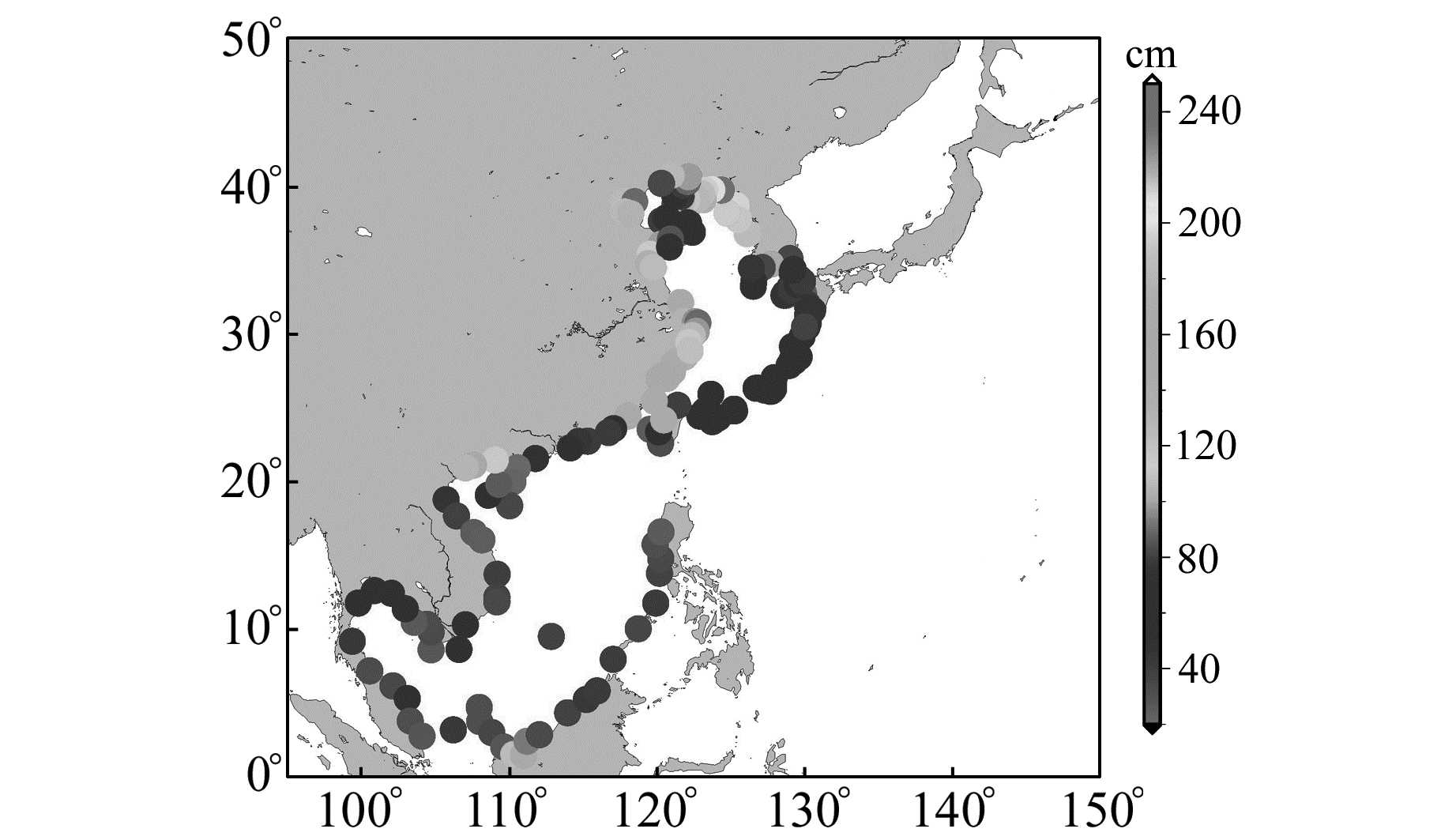
利用式(3)计算中国海及西太平洋海域12个主要分潮的调和常数,其中M2、S2、K1、O1分潮的振幅分布见图 2。
|
图 2 ERS系列卫星沿轨分析调和常数与验潮站的比较 Fig. 2 RSS of tidal height differences of 4 major constituents between interpolated constituents from ERS series of altimeter data and tide gauge constituents |
利用交叉点处上升与下降轨所得调和常数的差值可以评估分析结果的精度。选取研究区域内953个交叉点位置进行统计分析,结果见表 3。可以看出,太阳分潮S2、K1分潮振幅精度略差,分别为10.486 cm和13.979 cm,其他分潮的振幅精度均在5 cm以内。除S2、K1、K2外,各分潮潮高不符值[6]均在5 cm以内。整体而言,计算得到的调和常数中,太阴分潮M2、N2、O1、Q1比太阳分潮S2、K2、K1、P1精度高。除了主要太阳分潮S2、S1外,K1/P1/Sa与K2/SSa这两组分潮在混叠后也具有很强的相关性,从相位很难获取分辨它们的有用信息。从沿轨分析结果上看,利用近15 a连续观测资料得到的K2和P1分潮潮高不符值内符合精度在4.18 cm和5.59 cm,与T/P结果相比略差[8]。表 4是利用交叉点位置测高数据正交响应分析结果分别与上升和下降弧段沿轨分析结果的比较。在交叉点位置,包含上升轨迹和下降轨迹所有数据的交叉点分析结果好于沿轨分析结果,可见交叉点不能看作是沿轨分析结果的简单平均。对于ERS系列卫星来说,重复采样周期正好是S2、S1分潮的整数倍,无法计算它们的调和常数,但是交叉点位置的采样规律能够起到削弱混叠效应的作用,它不是简单的等间隔采样,在这种条件下对混叠效应的削弱作用明显,因为在均匀采样下混叠信号集中于一些和真实潮汐信号相关的频率,而非均匀采样混叠信号均匀地分布到所有频段上,从而最大程度地降低了混叠信号的幅值,有利于真实潮汐信息的提取。另一方面,在交叉点上,参与分析的卫星测高数据是沿轨分析时的2倍,表明在相同时段下观测样本数量增加,分析结果的内符精度也会显著提高。
|
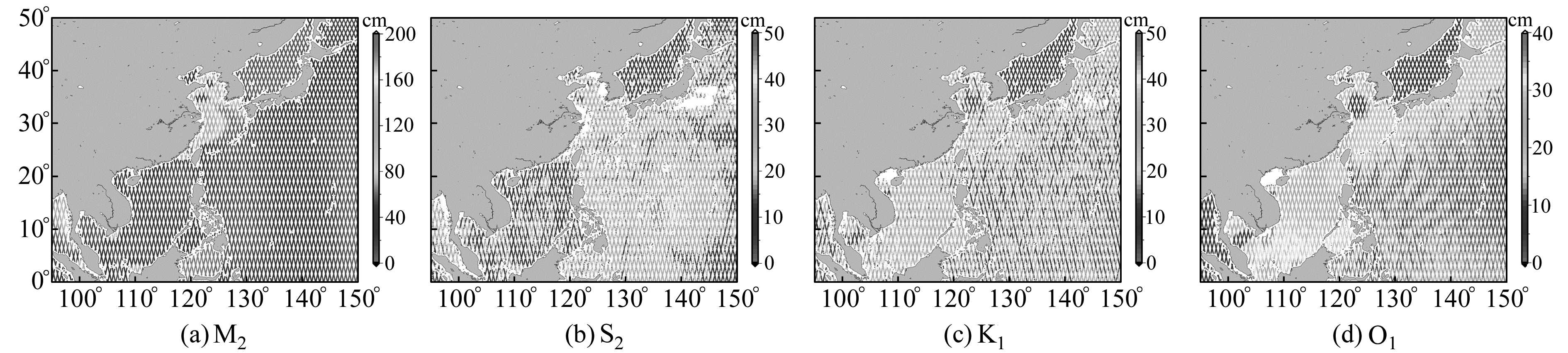
图 1 ERS系列卫星沿轨分析结果 Fig. 1 Amplitudes derived from ERS series altimeter data by along track analysis |
|
|
表 3 交叉点处上升与下降轨迹沿轨分析结果比较 Tab. 3 Difference between harmonics derived from ascending and descending passes at crossover points |
|
|
表 4 ERS交叉点分析结果与沿轨分析结果比较 Tab. 4 Difference between harmonics derived from crossover points and along tracks |
本文选取沿中国渤海、黄海、东海以及南海分布的200个验潮站4个主要分潮M2、S2、K1、O1的调和常数[16-17]。利用这些验潮站的各分潮潮高不符值的和方根(root sum square, RSS)进行统计比较[6],结果见表 5(单位cm)和图 2。为了验证本文计算结果,将T/P、Jason-1/2系列卫星自1992~2011年683个重复周期近19 a的数据进行沿轨正交响应分析,得到的调和常数与验潮站进行比较,结果见表 5。从图 2可以看到,从南海、东海、黄海再到渤海,随着海况和海域形状越来越复杂,计算的潮汐调和常数越来越不理想,特别是黄、渤海海域,由于潮波系统比较复杂导致潮汐性质变化急剧,全日潮、半日潮、混合潮一应俱全。由表 5可见,ERS系列卫星的结果略优于T/P系列卫星。分析表明,T/P系列卫星地面邻近平行轨迹间隔较大,在经向上仅有300 km的空间分辨率,明显低于ERS系列卫星,这使得T/P的沿轨分析结果在经向上过于平滑。同时,近海海域地理环境复杂,受海底地形、海况以及海域形状等多种因素的影响,非线性潮汐动力学特征明显,导致测高数据不连续。在T/P卫星测高数据分辨不足的情况下,通过内插方法得到的结果不如精度稍差而数据分辨率高的数据内插的结果。因此,联合多源卫星测高数据建立海潮模型,ERS-2、Envisat-1以及GFO等重复周期和地面采样规律的卫星势必会起到积极的作用。
|
|
表 5 ERS系列卫星与T/P系列卫星计算的潮汐调和常数与验潮站的比较 Tab. 5 Comparison between tide gauge constituents and interpolated constituents from ERS and T/P series of altimeter data |
本文利用正交响应分析对ERS-2、Envisat-1数据进行沿轨分析,得到中国海及西太平洋海域的潮汐分布。结果表明,除S2、K1分潮外,太阳同步轨道测高卫星能够提取出可靠和分布合理的潮汐调和常数。与T/P系列卫星相比,ERS系列卫星的相邻平行地面轨迹在赤道上的经度差为0.7°,在高纬度地区仅为0.5°。随着新一代ERS后续卫星SARAL以及Cryosat-2卫星数据的发布和积累,联合多源测高数据能够为建立高精度的局部海潮模型提供资料,从而为其他高精度大地测量技术提供潮汐改正。
| [1] |
Stammer D, Ray R D, Anderson O B, et al. Accuracy Assessment of Global Barotropic Ocean Tide Models[J]. Rev Geophys, 2014, 52: 1-40 DOI:10.1002/rog.v52.1
(  0) 0) |
| [2] |
Parke M E, Stewart R H, Farless D L, et al. On the Choice of Orbits for an Altimetric Satellite to Study Ocean Circulation and Tides[J]. J Geophys Res, 1987, 92: 11693-11707 DOI:10.1029/JC092iC11p11693
(  0) 0) |
| [3] |
Andersen O B. Ocean Tides in the Northern North Atlantic and Adjacent Seas from ERS 1 Altimetry[J]. J Geophys Res, 1994, 99(C11): 22557-22573 DOI:10.1029/94JC01433
(  0) 0) |
| [4] |
Shepherd A, Peacock N R. Ice Shelf Tidal Motion Derived from ERS Altimetry[J]. J Geophys Res, 2003, 108(C6): 3198 DOI:10.1029/2001JC001152
(  0) 0) |
| [5] |
Ray R D. Tidal Analysis Experiments with Sun-Synchronous Satellite Altimeter Data[J]. J Geod, 2007, 81: 247-257 DOI:10.1007/s00190-006-0105-1
(  0) 0) |
| [6] |
Andersen O B, Woodworth P L, Flather R A. Intercomparison of Recent Ocean Tide Models[J]. J Geophys Res, 1995, 100: 25261-25282 DOI:10.1029/95JC02642
(  0) 0) |
| [7] |
Andersen O B, Scharroo R. Range and Geophysical Corrections in Coastal Regions, and Implications for Mean Sea Surface Determination, in Coastal Altimetry[M]. New York: Springer, 2010
(  0) 0) |
| [8] |
Fang G H, Wang Y G, Wei Z X, et al. Empirical Cotidal Charts of the Bohai, Yellow, and East China Seas from 10 Years of TOPEX/Poseidon Altimetry[J]. J Geophys Res, 2004, 109(C11): 227-251
(  0) 0) |
| [9] |
Munk W H, Cartwright D E. Tidal Spectroscopy and Prediction[J]. Phil Tran Roy Soc London, 1966, 259(1105): 533-581 DOI:10.1098/rsta.1966.0024
(  0) 0) |
| [10] |
Groves G W, Reynolds R W. An Orthogonalized Convolution Method of Tide Prediction[J]. J Geophys Res, 1975, 80(30): 4131-4138 DOI:10.1029/JC080i030p04131
(  0) 0) |
| [11] |
Cartwright D E, Ray R D. Oceanic Tides from Geosat Altimetry[J]. J Geophys Res, 1990, 95: 3069-3090 DOI:10.1029/JC095iC03p03069
(  0) 0) |
| [12] |
李培良, 左军成. 南海TOPEX/POSEIDON高度计资料的正交响应法潮汐分析[J]. 海洋与湖沼, 2002, 33(3): 287-295 (Li Peiliang, Zuo Juncheng. Orthogonalized Convolution Method for Analysis of South China Sea Tidal Data from Topex/Poseidon[J]. Oceanologia et Limnologia Sinica, 2002, 33(3): 287-295)
(  0) 0) |
| [13] |
CERSAT. Altimeter & Microwave Radiometer ERS Products: User Manual[Z]. Frascat: ESRIN, 2001
(  0) 0) |
| [14] |
ESA. ENVISAT RA2/MWR Product Handbook[Z]. Frascat: ESRIN, 2004
(  0) 0) |
| [15] |
金涛勇. 多源海洋观测数据确定全球海平面及其变化的研究[D]. 武汉: 武汉大学, 2010 (Jin Taoyong. Research on Global Mean Sea Level and Its Change from Multi-Oceanic Observations[D]. Wuhan: Wuhan University, 2010)
(  0) 0) |
| [16] |
张继才. 三维正压潮汐潮流伴随同化模型数值建模及应用研究[D]. 青岛: 中国海洋大学, 2008 (Zhang Jicai. Development and Application of a Three-Dimensional Numerical Barotropic Adjoint Assimilation Tidal Model[D]. Qingdao: Ocean University of China, 2008) http://cdmd.cnki.com.cn/Article/CDMD-10423-2008176302.htm
(  0) 0) |
| [17] |
Fang G H, Kwok Y K, Yu K J. Numerical Simulation of Principal Tidal Constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand[J]. Continental Shelf Research, 1999, 19: 845-869 DOI:10.1016/S0278-4343(99)00002-3
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

