GRACE重力卫星能以前所未有的精度和时空分辨率观测全球时变重力场信号,为全球表层质量迁移和重新分布研究提供直接观测手段[1-3]。利用卫星重力对陆地水变化进行研究主要基于GRACE数据中观测到的最大信号来自地表及地下质量变化[4]。但是,由于GRACE数据在垂直分辨率上的限制[5],其不能有效区分TWS(陆地水储量)不同储水形式产生的异常,如地表水、地下水、土壤水分、冻雪等。通过同化大量地表和卫星观测资料,目前的水文模型已可以模拟全球和区域的土壤水储量变化和冰雪质量变化(如GLDAS系列模型和CPC水文模型)[6-7]。少数水文模型还考虑了农业灌溉等人类活动对土壤含水量的影响以及气候变化驱动下的地下水储量的变化(如WGHM和CLM等模型)[8-9]。
近年来,利用水文模型数据提高GRACE数据纵向分辨率的研究得到长足发展,但也存在问题。例如,没有任何一个水文模型(GLDAS和CLM)可以被校准到地表现场测量值,模型建立也未考虑人为因素或者动态湖泊及水库的贡献;GLDAS模型不能模拟地下水和河道库水变化[7],且CLM模型过高估计了地表水蒸发,不能充分模拟土壤蒸发分区、林冠蒸发与蒸腾等因素[10]。因此,针对水文模型数据自身的质量,包括其驱动数据(降水、气温)及模拟结果(径流、土壤含水量及蒸散发量),国内外学者[11-13]通过不同模型之间的对比,或模型输入参数与地面台站观测数据的对比得出,不同水文模型在不同河流流量及流域范围内数据有很大差别,且精度有显著的区域性差异;不同季节的模型精度差异较大,春夏季能量模拟效果好于秋冬季,且地势相对低平地区的模拟效果要好于海拔较高的青藏高原和纬度较高的地区;各类模型中,GLDAS的降水数据总体性能最好,其数据精度能满足蒸散发研究的需要,比地面气象站点观测具有更好的时空连续性。
在青藏高原地区,国内外学者已经开展基于GRACE监测该地区季节性与长期TWS变化方面的研究,如喜马拉雅冰川消融[14]及青藏高原内陆陆地水增加[15],所使用的GRACE数据版本、研究时段以及平滑方法和半径有所不同,更重要的是水文模型的选取不同,造成结果存在一定的差异。基于此,本文利用GRACE及气象数据,从水文模型的适用性出发,评估目前常用的GLDAS模型在青藏高原的性能,以期在该地区利用GLDAS模型提高GRACE的垂直分辨率。
1 数据与方法 1.1 GLDASGLDAS水文模型是由美国宇航局哥达德飞行中心(Goddard space flight center, NASA)和美国国家环境预报中心(national centers of environmental prediction,NCEP)共同建立的全球水文模型。GLDAS使用的气象要素、降水、辐射等驱动数据基于多源观测、再分析资料和大气同化产品。降水数据来源于卫星观测降水数据以及NOAA气候预报中心的业务化融合分析降水资料(CMAP),短波和长波辐射数据由空军天气署农业气象模拟系统(AGMET)提供的算法结合云和雪的产品估算得到,大气同化资料来源于哥达德飞行中心的大气数据同化系统(GEOS)、NCEP全球大气数据同化系统(GDAS)和欧洲中尺度天气预报中心(ECMWF)数据。GLDAS陆面数据同化系统共调用了CLM、NOAH、Mosaic 3个陆面过程模式以及VIC水文模型。该模式利用陆地表面建模和数据同化技术,其发布的数据主要包括输入与输出陆地表面的各项参数(土壤湿度、土壤温度、蒸发量、降雨、径流和雪量等)。可见,虽然GLDAS融合了大量多源气候资料,但主要以卫星观测数据为主,难免存在空间分布不均、时间跨度不一且离散等问题。
1.2 GRACE采用CSR提供的时间跨度为2003-01~2012-12的GRACE RL05模型,系数最高阶次为60阶,且扣除了潮汐影响和非潮汐的大气和海洋影响。由于C20项误差较大,将此项替换为SLR观测结果[16],而模型一阶项则采用Swenson等[17]提供的一阶项系数。由于模型受卫星轨道误差和球谐系数截断误差等影响,采用多项式去条带滤波[18]和高斯平滑滤波[4]相结合的方法对模型系数进行滤波,其中高斯滤波半径取300 km。利用GRACE估算冰盖质量变化结果的不确定性在很大程度上受不同GIA模型的影响,选取Geruo等[19]的GIA模型进行校正。
1.3 台站气温与降雨台站资料来源于国家气象信息中心,包括中国756个基本、基准地面气象观测站及自动站1961年至今的气温与降雨月值资料。通过克里金插值同时引入数字高程资料以消除地形对气温空间插值的影响,并利用全球历史气候网数据对各站点进行扩充,以减小边界资料稀少造成的边界效应,其空间分辨率为0.5°×0.5°。
1.4 相关性与Nash-Sutcliffe效率系数(NSE)为有效评估GLDAS与GRACE 2个数据源在研究区的符合程度,计算二者的相关系数用以反映利用不同手段监测TWS变化之间的密切程度。此外,本文对GRACE去除GLDAS模型后的反演结果进行均方根误差减小(RMSreduction)计算[20]:
| $ \text{RM}{{\text{S}}_{\text{reduction}}}=\frac{\text{RM}{{\text{S}}_{\text{GRAC}{{\text{E}}_{i}}}}-\text{RM}{{\text{S}}_{\text{GRAC}{{\text{E}}_{i}}}}-\text{GLDA}{{\text{S}}_{i}}}{\text{RM}{{\text{S}}_{\text{GRAC}{{\text{E}}_{i}}}}} $ | (1) |
式中,RMSGRACEi与RMSGRACEi-GLDASi为GRACE去除GLDAS模型前后结果的均方根误差,RMSreduction越接近1表示二者符合度越高。Nash-Sutcliffe效率系数(NSE)通常被用作水文模型的效率评价指标,也可用于水文模型约束参数与地面实测数据之间的结果评定。NSE作为一个标准化统计方法,其系数变化范围为-∞~1。理想情况下,1值对应于水文模型输入参数与实测值的完美匹配[21]:
| $ \text{NSE}=1-\frac{\sum\limits_{i=1}^{n}{{{(\text{In }\!\!\_\!\!\text{ sit}{{\text{u}}_{i}}-\text{GLDA}{{\text{S}}_{i}})}^{2}}}}{\sum\limits_{i=1}^{n}{{{(\text{In }\!\!\_\!\!\text{ sit}{{\text{u}}_{i}}-\overline{\text{In }\!\!\_\!\!\text{ situ}})}^{2}}}} $ | (2) |
式中,In_situi与GLDASi分别为地面实测与水文模型输入数据在第i个月的降雨或气温数据,而
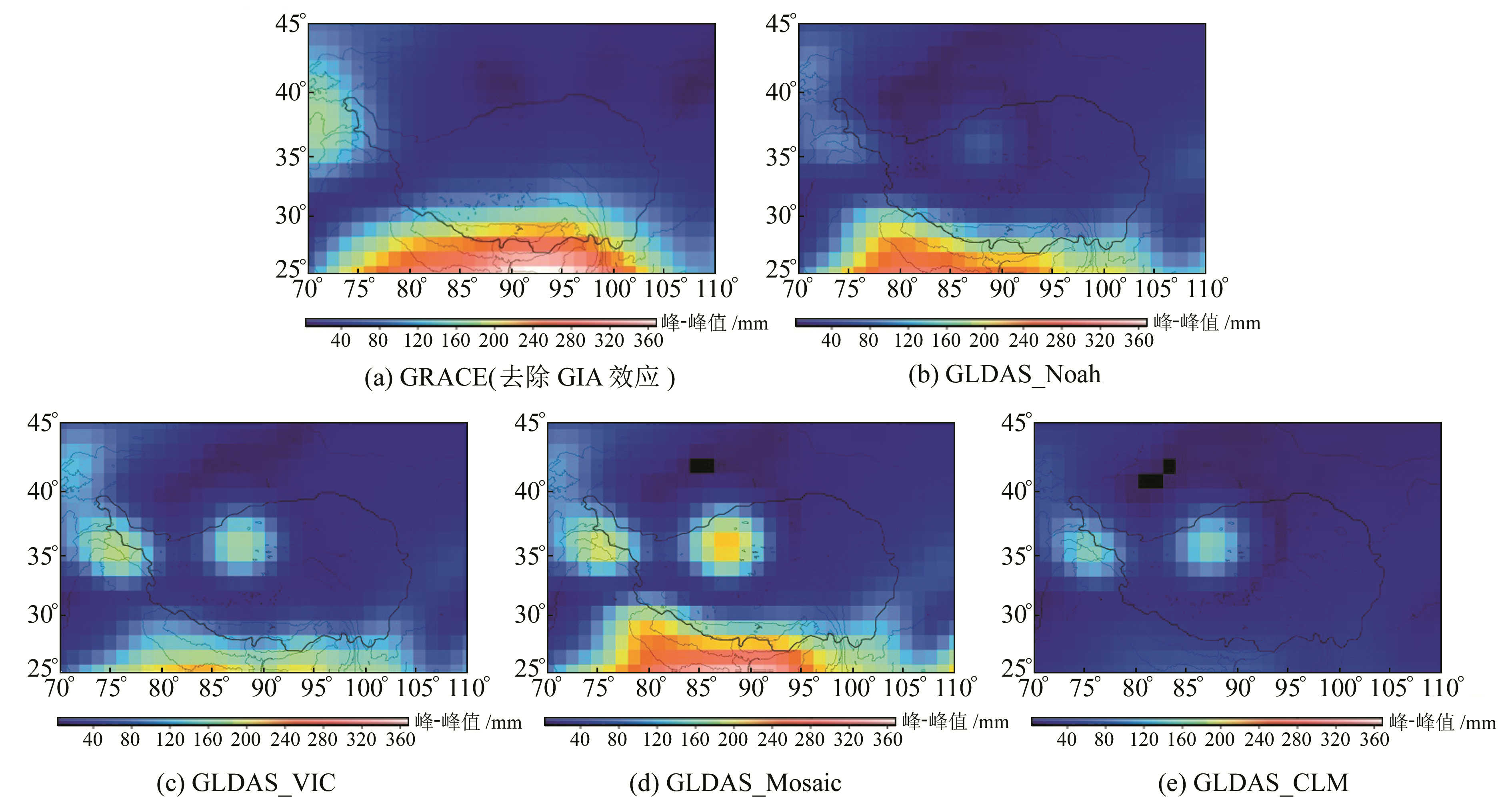
图 1为由GRACE(去除GIA效应)及GLDAS模型的Noah、VIC、Mosaic及CLM 4个版本反演得到的青藏高原地区2003~2012年TWS周年变化的峰-峰值空间分布。可见,GRACE反演得到的TWS与GLDAS模型除CLM以外的3个版本周年幅值空间整体分布较为一致,但存在局部不同。整体上,青藏高原由于海拔高、温度低及降雨少,周年变化峰-峰值平均值为80 mm;南部地区TWS周年峰-峰值变化能达到约300 mm,主要集中在喜马拉雅山地区南端,由于该地区冰川与积雪的季节性融化以及南端较大区域的恒河流域,因此存在显著的季节性变化。GLDAS/Noah相对其他版本周年幅值变化总体上与GRACE一致,而CLM版本由于与其他模型有较大差距,故在后续评估中忽略。
|
图 1 青藏高原地区2003~2012 TWS周年变化的峰-峰值空间分布 Fig. 1 Peak-to-peak amplitude of annual cycle of TWS over the Tibet plateau from January 2003 to December 2012 |
区域核函数方法是目前用于研究区域质量变化时间序列的主要方法。平均(敏感)核函数方法的主要思想是基于预先定义的一个明确(exact)的平均核函数(区域内为1、区域外为0的等间距网格点),结合高斯平滑抑制GRACE高阶误差。Swenson等[22]为克服平滑半径增大导致的泄漏误差增加,给出了基于最小二乘原理的最优平均核函数(optimizing the averaging kernel)。本文假设研究区域内的TWS高度为1 cm,区域外为0,对该网格数据进行球谐展开并进行与GRACE处理相同的过程,得到研究区域内的平均核函数分布(图 2),并以此提取区域空间平均后的时间序列。

|
图 2 提取青藏高原区域质量变化时间序列的平均核函数 Fig. 2 The averaging kernel used to find time series of mass variability in Tibet plateau |
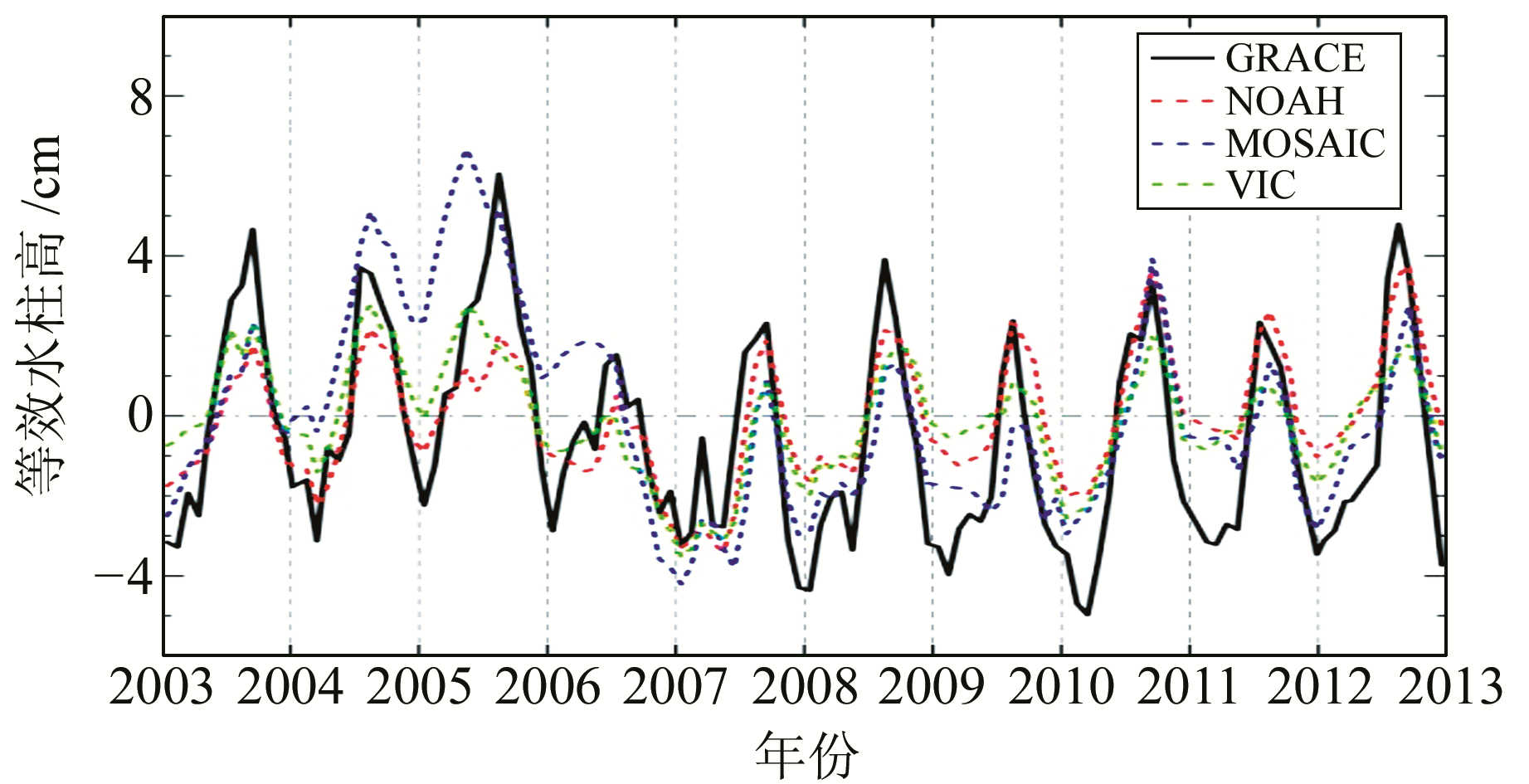
利用GRACE及GLDAS提取的青藏高原TWS时间序列(图 3)表明,GRACE与GLDAS 3个版本的幅值与相位模式存在不同程度的对应关系。由于青藏高原主要受到冰川积雪与内陆湖泊TWS变化的影响,因此2个数据源呈现出2003~2005年TWS以较高幅值变化,以及2005年以后明显增加的趋势。此外,GRACE反演得到的TWS幅值要明显高于GLDAS水文模型,这是由于GRACE监测到的是地表至地下所有水文参数的整体效应,而GLDAS模型涵盖了部分效应(土壤湿度与降雪)。根据§1.4的评估方法,对GEACE与GLDAS 3个版本TWS结果之间的相关系数、RMSreduction、趋势变化率、周年幅值与相位进行计算分析(表 1)可见,GLDAS/Noah各项指标与GRACE更相近,而从时间序列也能发现GLDAS/Noah不管是周年还是长周期趋势,都与GRACE对应较好;GLDAS/VIC与GRACE的对比结果相比GLDAS/Noah各项指标稍偏低,但比GLDAS/MOSAIC要高。
|
图 3 基于平均核函数的GRACE及GLDAS提取青藏高原TWS时间序列 Fig. 3 Time series of TWS in Tibet plateau using GRACE and GLDAS based on averaging kernel |
|
|
表 1 GRACE与GLDAS之间的相关系数、RMS减小值、趋势变化率以及周年幅值与相位 Tab. 1 The correlation coefficients, RMS reduction, the secular trend, annual amplitude and phase between GRACE and GLDAS |
从GLDAS输入量出发,聚焦模型约束参数与地面观测之间的相关性。由于GLDAS模型未模拟地下水及河道储水量,且约束输入参数(降雨与气温)也未与地面观测值进行校准,因此,GLDAS/Noah模型虽然相比其他版本与GRACE更为接近,但也存在高估或低估实际TWS变化的可能。基于地面气象观测数据以及NSE评价方法,能够有效评估甚至提高水文模型的适应性。
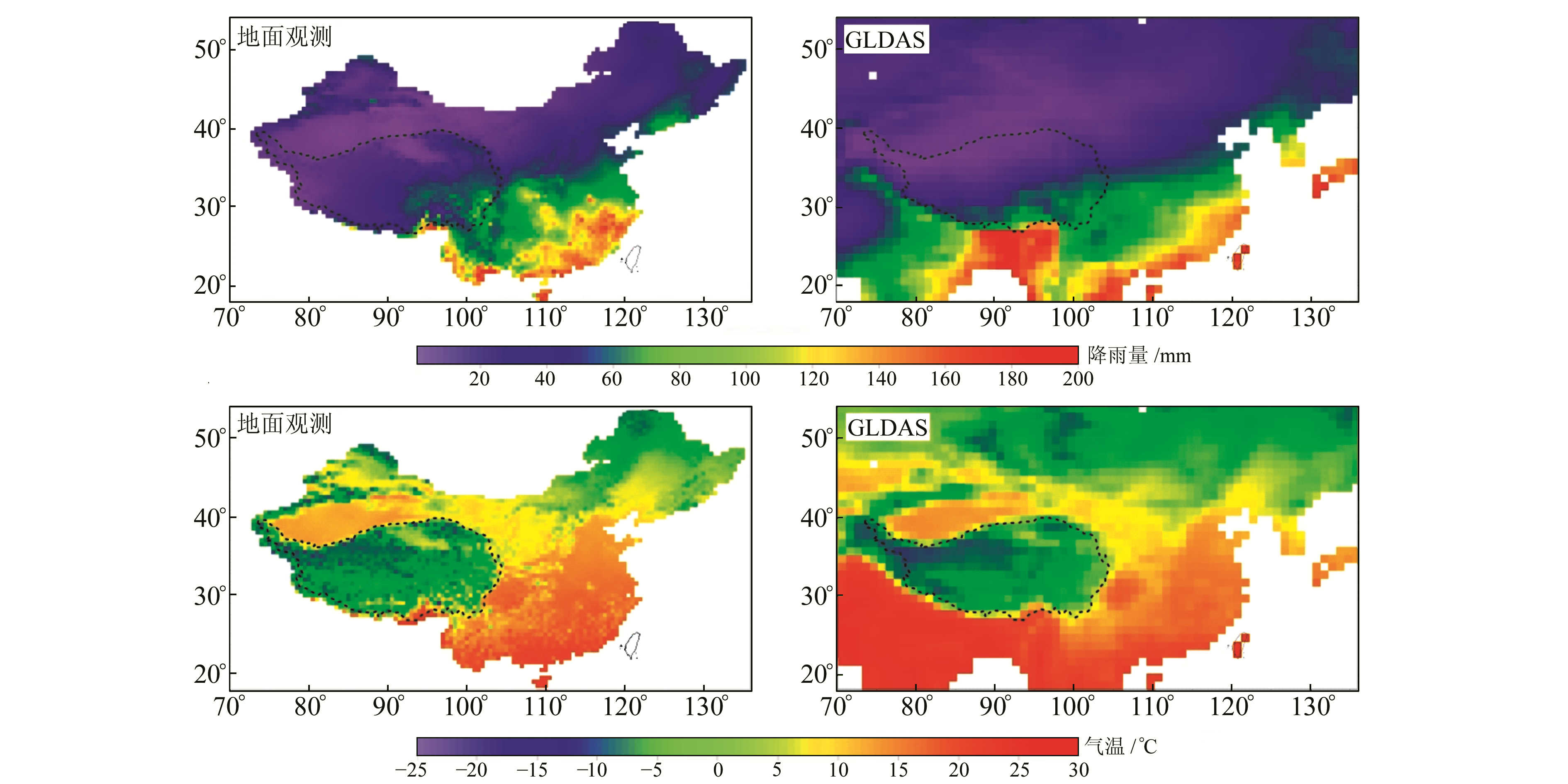
图 4给出了中国地区降雨及气温的台站观测与GLDAS模型的月平均空间分布,地面台站数据的空间分辨率为0.5°×0.5°,高于GLDAS模型1.0°×1.0°的分辨率。对于青藏高原地区,月平均降雨量约40 mm(图 4(a)),月平均气温变化在0 ℃左右(图 4(b))。由于地面观测值分辨率高,能够识别出局部地区的降雨与气温变化,而GLDAS模型分布较为平缓,整体上与地面观测值相似,但不能突出局部细节。
|
图 4 地面观测与GLDAS模型的降雨与温度分布(2003-07) Fig. 4 Rainfall and temperature of in-situ measurements and GLDAS input forcing parameters on July 2003 |
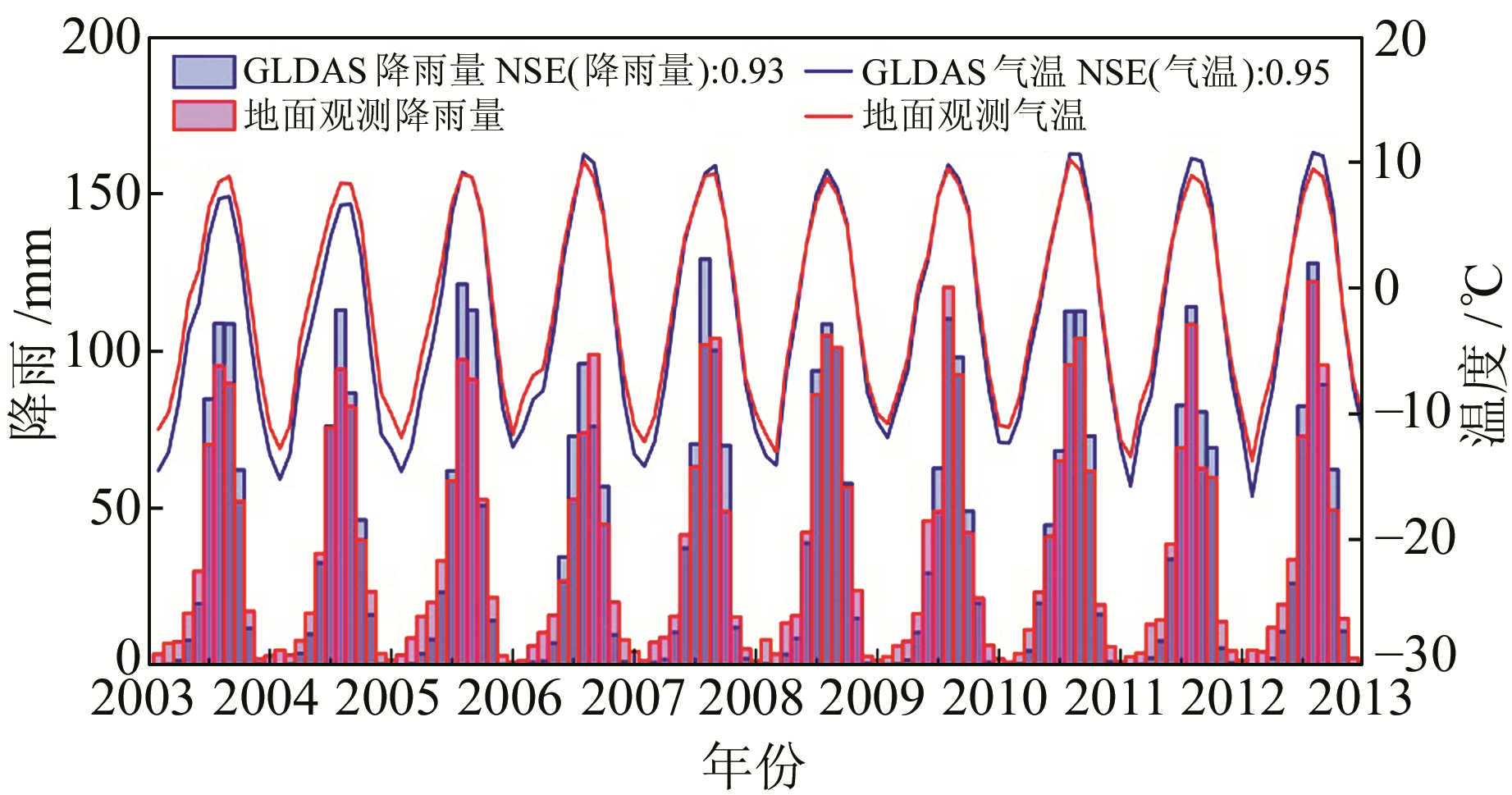
对青藏高原地区地面与GLDAS模型的气温与降雨格点数据集进行月平均后得到的时间序列如图 5所示,地面观测与GLDAS模型输入约束参数之间显示出较好的一致性,但在夏季时期二者幅值存在一定的差异,主要表现为GLDAS模型月降雨量在夏季高于地面台站观测数据,而在其他季节偏少;对于气温变化,二者的不同主要体现在夏冬两季1~2 ℃的偏差。此外计算GLDAS模型与地面观测之间的NSE,结果表明GLDAS模型的降雨量与气温约束参数整体上与地面观测数据有较高的相关性,验证了GLDAS模型数据在青藏高原地区的适用性。
|
图 5 地面台站与GLDAS约束参数的降雨和气温时间序列 Fig. 5 Time serise of rainfall and temperature of in-situ measurements and GLDAS input forcing parameters |
针对青藏高原地区冰雪与内陆湖泊质量变化问题,利用GRACE及气象数据评估GLDAS水文模型在该地区的适用性。得到以下结论:
1) GRACE与GLDAS水文模型提取的TWS之间的相关性及差异结果表明,GLDAS/Noah各项指标与GRACE更为相近,相比GLDAS/Noah,GLDAS/VIC与GRACE的各项指标稍微偏低,但比GLDAS/Mosaic高,而CLM版本与GRACE以及其他版本存在较大差距。
2) 利用与地面观测数据的相关性及误差评估水文模型输入参数的降雨与气温,结果显示除夏冬两季存在幅值差异外,整体上周年幅值与相位都存在较高的NSE系数,表明GLDAS模型的降雨及气温输入参数与地面观测数据有较高的一致性。
致谢 GRACE、GLDAS模型数据以及地面气象资料分别由CSR、NASA以及中国气象局国家气象信息中心提供,在此表示感谢。
| [1] |
Tapley B D, Bettadpur S, Watkins M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9)
(  0) 0) |
| [2] |
宁津生. 卫星重力探测技术与地球重力场研究[J]. 大地测量与地球动力学, 2002, 22(1): 1-5 (Ning Jinsheng. The Satellite Gravity Surveying Technology and Research of Earth's Gravity[J]. Journal of Geodesy and Geodynamics, 2002, 22(1): 1-5)
(  0) 0) |
| [3] |
许厚泽. 卫星重力研究:21世纪大地测量研究的新热点[J]. 测绘科学, 2002, 22(3): 1-3 (Xu Houze. Satellite Gravity Missions-New Hotpoint in Geodesy[J]. Science of Surveying and Mapping, 2002, 22(1): 1-3)
(  0) 0) |
| [4] |
Wahr J, Swenson S, Zlotnicki V, et al. Time-Variable Gravity from GRACE: First Results[J]. Geophysical Research Letters, 2004, 31: L11501
(  0) 0) |
| [5] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30205-30229 DOI:10.1029/98JB02844
(  0) 0) |
| [6] |
Fan Y, Dool H. Climate Prediction Center Global Monthly Soil Moisture Data Set at 0.5° Resolution for 1948 to Present[J]. Journal of Geophysical Research, 2004, 109(D10)
(  0) 0) |
| [7] |
Rodell M, Houser P R, Jambor U, et al. The Global Land Data Assimilation System[J]. Buletin of the American Meteorological Society, 2004, 85(3): 381-394 DOI:10.1175/BAMS-85-3-381
(  0) 0) |
| [8] |
Doll P, Kaspar F, Lehner B. A Global Hydrological Model for Deriving Water Availability Indicators: Model Tuning and Validation[J]. Journal of Hydrology, 2003, 270(1): 105-134
(  0) 0) |
| [9] |
Bonan G B, Drewniak B, Huang M. Technical Description of Version 4. 5 of the Community Land Model (CLM)[R]. NCAR Technical Note NCAR/TN-503+STR, Boulder, Colorado, 2013
(  0) 0) |
| [10] |
Swenson S, Lawrence D. Assessing a Dry Surface Layer-Based Soil Resistance Parameterization for the Community Land Model Using GRACE and FLUXNET-MTE Data[J]. Journal of Geophysical Research:Atmospheres, 2013, 119(17): 10299-10312
(  0) 0) |
| [11] |
王婉昭, 高艳红, 许建伟. 青藏高原及其周边干旱区气候变化特征与GLDAS适用性分析[J]. 高原气象, 2013, 32(3): 635-645 (Wang Wanzhao, Gao Yanhong, Xu Jianwei. Applicability of GLDAS and Climate Change in the Qinghai-Xizang Plateau and Its Surrounding Arid Area[J]. Plateau Meteorology, 2013, 32(3): 635-645 DOI:10.7522/j.issn.1000-0534.2013.00054)
(  0) 0) |
| [12] |
王文, 汪小菊, 王鹏. GLDAS月降水数据在中国区的适用性评估[J]. 水科学进展, 2014, 25(6): 769-778 (Wang Wen, Wang Xiaoju, Wang Peng. Assessing the Applicability of GLDAS Monthly Precipitation Data in China[J]. Advances in Water Science, 2014, 25(6): 769-778)
(  0) 0) |
| [13] |
Bi H, Ma J, Zheng W, et al. Comparison of Soil Moisture in GLDAS Model Simulations and In-situ Observations over the Tibetan Plateau[J]. Journal of Geophysical Research :Atmospheres, 2016, 121(6): 2658-2678 DOI:10.1002/2015JD024131
(  0) 0) |
| [14] |
Matsuo K, Heki K. Time-Variable Ice Loss in Asian High Mountains from Satellite Gravimetry[J]. Earth & Planetary Science Letters, 2010, 290(1-2): 30-36
(  0) 0) |
| [15] |
钟敏, 段建宾, 许厚泽, 等. 利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势[J]. 科学通报, 2009, 54(9): 1290-1294 (Zhong Min, Duan Jianbin, Xu Houze, et al. Trend of China Land Water Storage Redistribution at Medi- and Large-Spatial Scales in Recent Five Years by Satellite Gravity Observations[J]. Chinese Science Bulletin, 2009, 54(5): 1290-1294)
(  0) 0) |
| [16] |
Cheng M K, Tapley B D, Ries J C. Deceleration in the Earth's Oblateness[J]. Journal of Geophysical Research, 2013, 118(2): 740-747
(  0) 0) |
| [17] |
Swenson S, Famiglietti J, Basara J, et al. Estimating Profile Soil Moisture and Groundwater Variations Using GRACE and Oklahoma Mesonet Soil Moisture Data[J]. Water Resources Research, 2008, 44(1)
(  0) 0) |
| [18] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letters, 2006, 33(8)
(  0) 0) |
| [19] |
Geruo A, Wahr J, Zhong S. Computations of the Viscoelastic Response of a 3-D Compressible Earth to Surface Loading: An Application to Glacial Isostatic Adjustment in Antarctica and Canada[J]. Geophysical Journal International, 2013, 192(2): 557-572 DOI:10.1093/gji/ggs030
(  0) 0) |
| [20] |
Dam T, Wahr J, Lavallée D. A Comparison of Annual Vertical Crustal Displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B3)
(  0) 0) |
| [21] |
Ahmed M, Sultan M, Yan E, et al. Assessing and Improving Land Surface Model Outputsover Africa Using GRACE, Field, and Remote Sensing Data[J]. Surveys in Geophysics, 2016, 37(3): 1-28
(  0) 0) |
| [22] |
Swenson S, Wahr J. Methods for Inferring Regional Surface-Mass Anomalies from Gravity Recovery and Climate Experiment (GRACE) Measurements of Time-Variable Gravity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B9)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


