2. 贵州大学资源与环境工程学院,贵阳市花溪区,550025
基于陆地重力观测手段获取近地表高精度重力场变化,是研究地壳内部物质运移和属性变化的重要手段之一。绝对重力观测技术在本世纪迅速发展,使得应用陆地重力重复观测手段获取高精度“微重力”时变信号成为可能。地表重力场随时间的微弱变化是一种典型的微重力信号[1],对于研究浅层质量变化过程应用较为广泛[2-5],但是用来研究地壳内部更深层(5~15 km)的场源过程则难度更大。在地表观测与深部场源相关的重力信号中,除可观测信号强度较弱外,如何定量分离浅部干扰也是一个重要问题。而以获取地震前兆为目的的地震重力测量,为获取较深层场源信号的变化特征,则需要深入研究该类微重力信号的观测与分离问题。
研究认为,地震、地下水、火山活动及各种构造运动和地壳垂直形变等地球动力学过程,都会引起一定程度的地球重力场变化[6-10]。本文主要研究如何通过改进陆地重力观测系统,来提取深部场源重力变化信号。通过对重力观测系统的敏感度分析和模型正演来提高深部介质物性变化的监测能力,并交叉运用多种观测手段,来减少反演结果的不确定性,其核心是提高地表重力观测对深部场源信号的信噪比。
1 重力观测的场源敏感性分析地表可观测的重力异常可以认为是地下介质剩余质量的积分。假如将地下介质离散化为体积相同的单元,每个单元在单位密度下对地表观测点的重力异常贡献为Ai,将每个单元的贡献大小求和后与全部单元贡献之比定义为累积敏感度f:
| $ f=\frac{100\cdot \sum\limits_{{{w}_{hi}}}^{w}{{{w}_{i}}{{A}_{i}}}}{\iint{{{w}_{i}}\text{d}}A} $ | (1) |
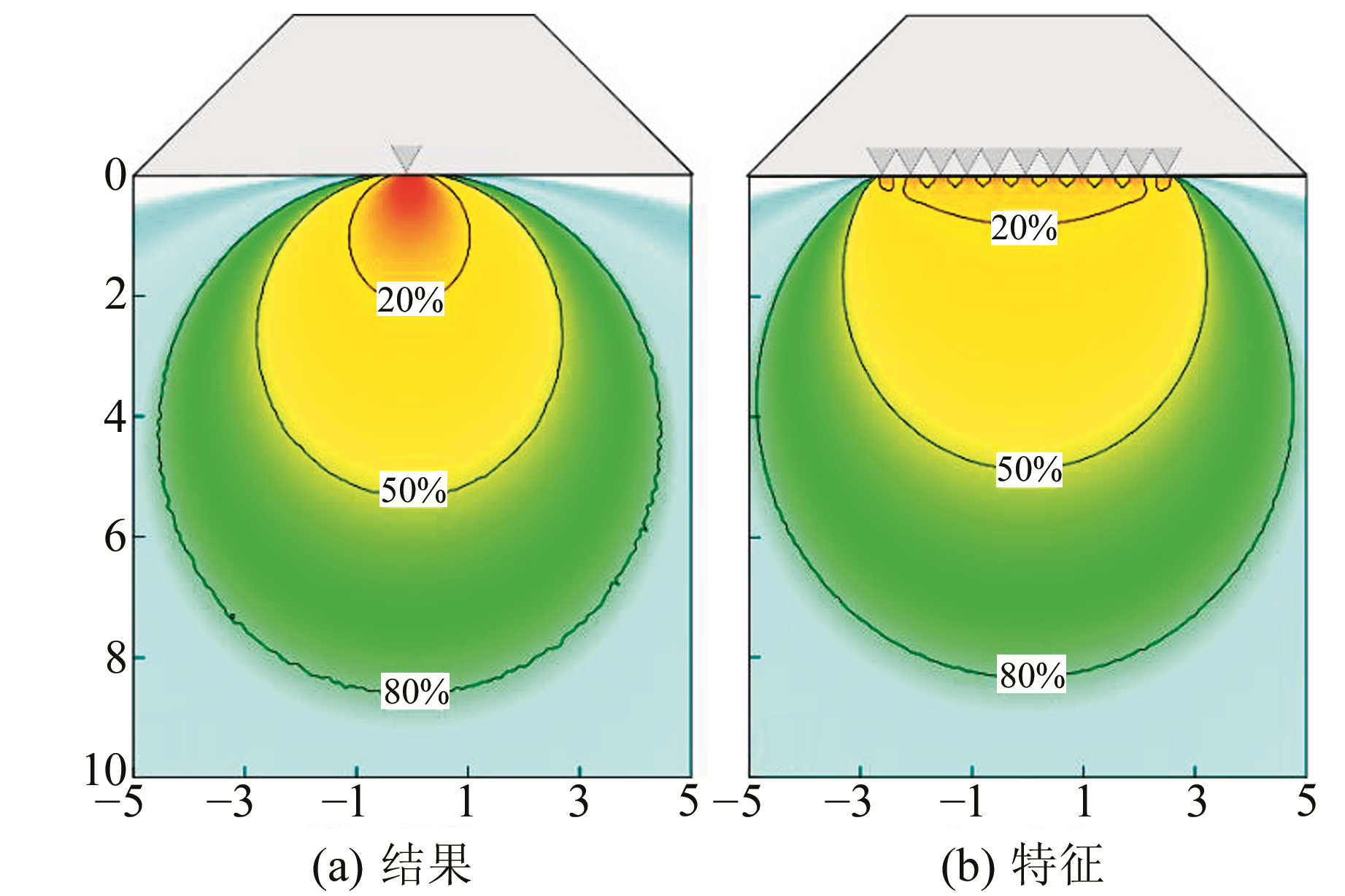
依据式(1)得到如图 1(a)所示的场源敏感度计算结果,图中横纵坐标与计算单元大小成比例关系,等值线的数值表示地表可观测异常的场源贡献百分比,即对等值线范围内单元异常的贡献进行积分后在总异常中的占比。可以看出,对于地表重力观测,地下介质的敏感度范围呈倒扇状分布,场源敏感性在水平方向衰减很快,大于垂直方向。图 1(a)中用颜色表示每个单元的贡献大小,红色表示对观测敏感度高,蓝色为敏感度低。容易看出,距离观测点越近的单元贡献越大,这意味着如果在近场源点发生密度变化,则相比距离较远的单元更敏感。如果在地表采用等间距排列方式构建的11个点观测系统,叠加观测后平均可得到图 1(b)所示的敏感度分布特征。可以看出,叠加后的观测系统可以有效降低浅场源物质的敏感度水平,提高深部场源可测量信号的信噪比。
|
图 1 重力观测的场源敏感度分析 Fig. 1 The sensitivity analysis of field source on the gravity observation |
场源敏感度分析方法给出了重力观测系统可探测场源能力的一种定量方法。利用这种方法,通过地表多个测点之间的组合观测,可以利用观测点之和差运算来调节观测网络的敏感区范围,进而形成可以聚焦特定时空位置的重力观测系统,也就是近年来所谓的变基线重力梯度方法[11]。
2 阵列式重力观测系统微重力观测系统设计通常都针对特定的探测目标,而不同空间位置的重力观测对地下场源敏感程度有显著差别,如果根据模型计算场源敏感度来设计多方式组合的重力观测系统,将更有利于识别特定时空尺度的场源重力信号。
基于以上原理,本文设计一种可用于探测时变重力场变化信号的“阵列式场地微重力综合观测系统”,简称“阵列式重力观测系统”。该系统联合运用物理、几何和水文3种观测方式,来减少地下场源微重力信号分离的不确定性。具体做法如下:选择具有较好观测条件的场地环境,联合绝对重力、相对重力、梯度、水准、GNSS和近地表流体等相互协调的组合重力观测系统。通过在场地内部构建小尺度重力与形变观测点阵,分离不同深部场源引起的重力变化信号,提高观测信号的信噪比,形成针对深部介质物性变化的监测能力。
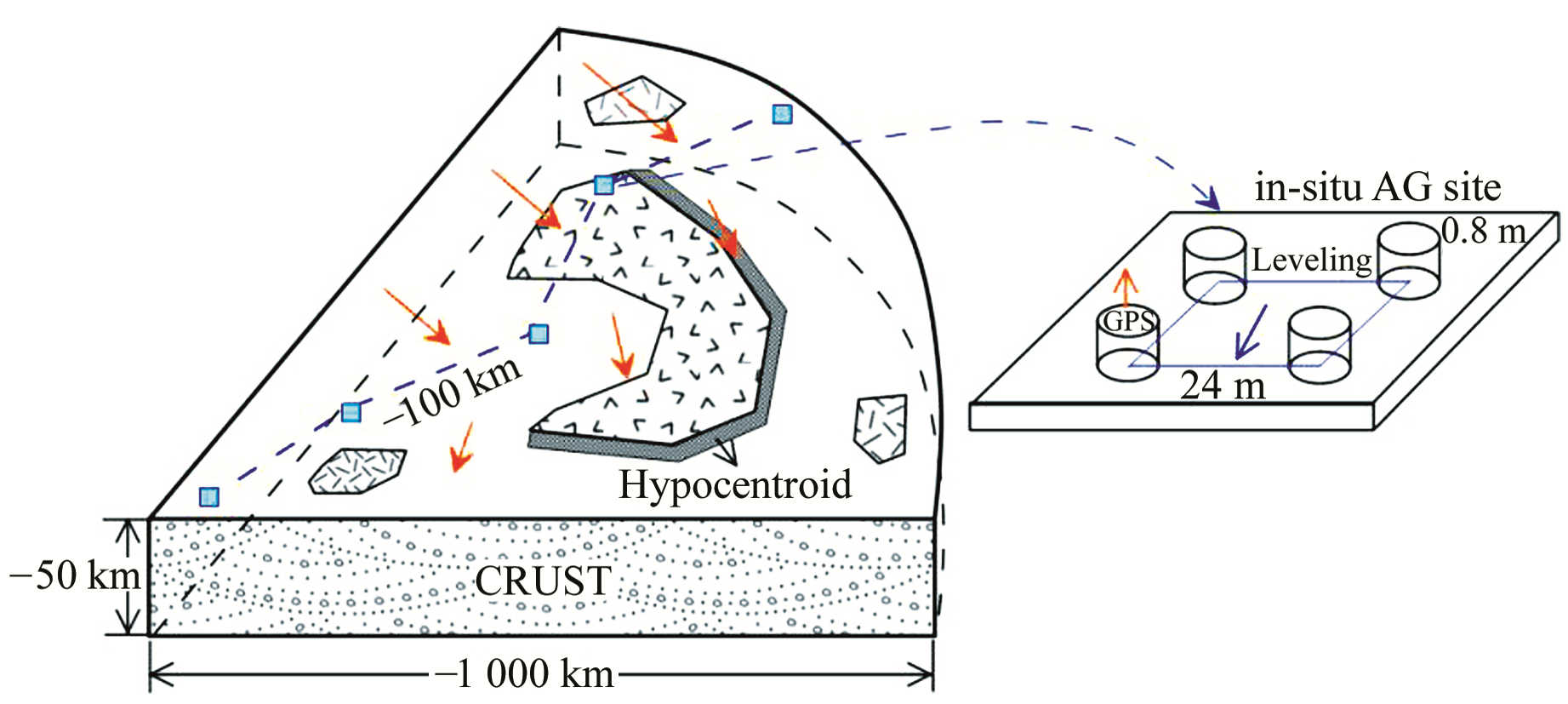
图 2是该系统的概念设计。将图中蓝色的传统重力观测点扩展为重力观测阵列,阵列之间的水平间距和垂直间距可以根据时间观测场源参数进行调节,不同深度场源信号在这种小尺度观测系统中的衰减差别是提高该系统敏感性的关键。表 1模拟了多个不同场源参数的圆盘模型在小尺度观测系统中的信号衰减特征。根据模型设计,在圆盘中心位置正上方都可以观测到约34 μGal的重力异常,但两个模型的场源参数差别很大,模型1的场源埋深为10 m,可以模拟常见的地下水过度开采引起的重力异常;而模型2的场源埋深为10 km,圆盘的半径为1 km,远小于当前地震重力测量的几十km点间距,应用现有重力观测网络虽然可以观测到该异常,但由于测网过于稀疏,很难判断该异常的场源位置。如果在水平和垂直位置分别设计两个阵列点,如表 1所示,浅部场源模型1则很容易通过近场地水平观测识别出来。在垂直方向,近地表场源随着高度的增加衰减也更快,而深部场源的重力异常信号在这种小尺度阵列式重力观测系统中则更多表现为较一致的信号特征,这也是该系统提高微重力观测信噪比的关键设计之一。
|
图 2 阵列式重力观测系统概念设计 Fig. 2 The conceptual design of gravity array observation system |
|
|
表 1 基于圆盘模型的理论重力异常计算 Tab. 1 The theory gravity anomaly on disk models |
此外,对于时变重力观测,通过地表几何观测和水文等辅助手段,还可以扣除地表变形和近地表土壤、地下水等环境干扰。在地震行业,主要应用目标是通过分离不同深部场源引起的重力变化信号,形成针对深部介质物性变化的监测能力,探索深部介质变化与地震活动的关联性。
3 场源模型测试和分析本文通过数值模型计算来讨论不同时空尺度下重力观测系统的设计与场源敏感区域的关系。
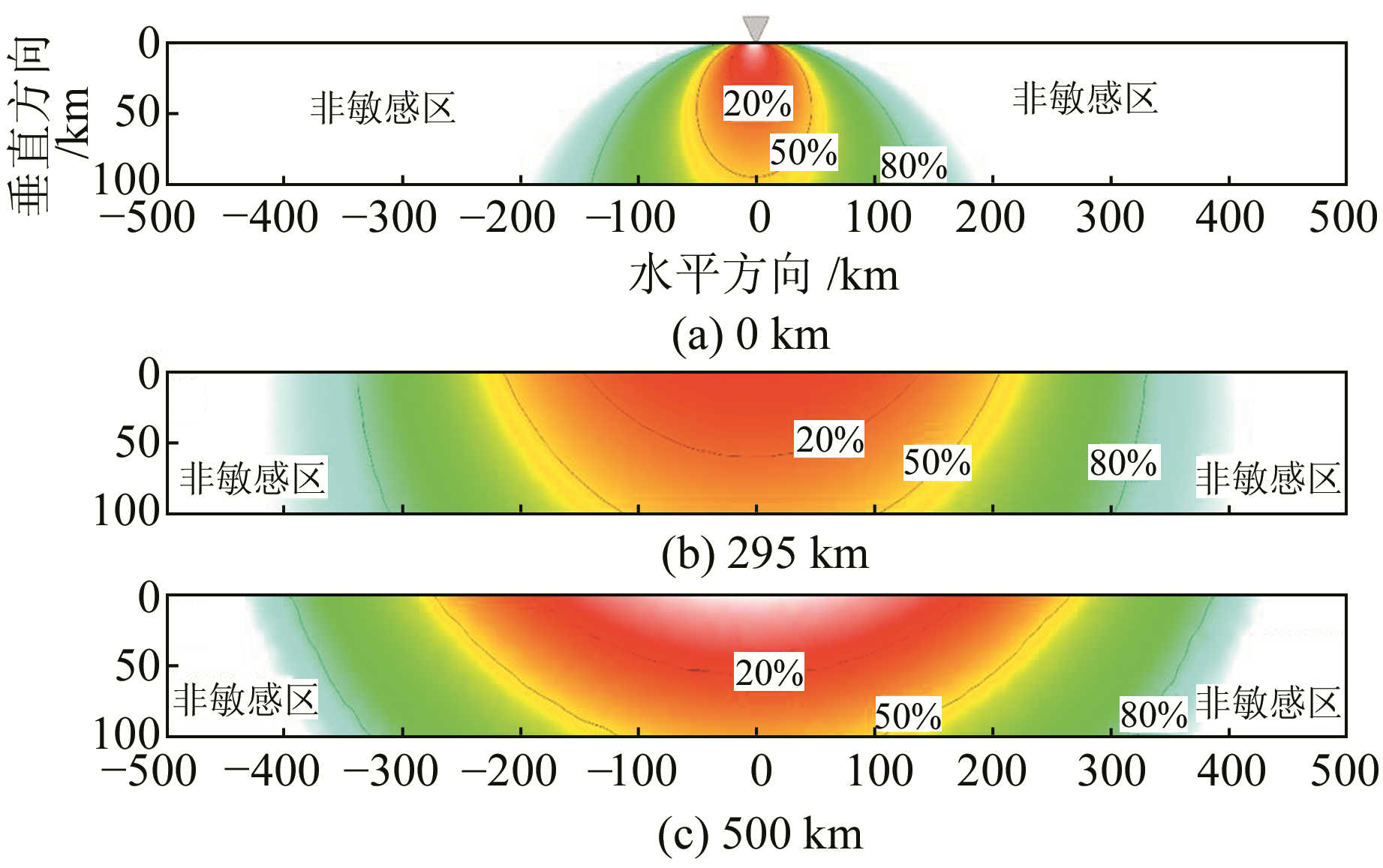
首先,通过模型计算地表不同高度的可探测场源敏感区特征。由于本文重点是讨论时变重力场信号的场源探测问题,而常见的地表重力观测和卫星重力观测都可以探测到μGal级重力时变信号,因此模拟了地表、295 km(GOCE卫星观测高度)、500 km(GRACE卫星观测高度)3个观测高度对地下100 km范围内的场源敏感度特征,如图 3所示。如果将累积敏感度参数f=80%范围内区域定义为敏感区,可以看出陆地重力观测和卫星重力观测对地壳内部场源的敏感性差别十分明显,地表、295 km和500 km高度重力观测的场源敏感水平尺度分别约为260 km、650 km和800 km。图 3(a)所示的陆地重力观测敏感区范围f=50%区域主要集中于测点下方,且在近地表水平方向敏感度随测点距离增加而迅速减小。相反,图 3(b)和3(c)所示的卫星观测高度重力敏感区域范围更集中于中上部区域,如在500 km观测高度,敏感度集中于近地表水平方向约800 km范围内。
|
图 3 不同观测高度的场源敏感性分析 Fig. 3 The sensitivity analysis of field source for the different vertical observed positions |
根据图 3给出的不同观测高度场源敏感度计算结果可以得到,虽然卫星重力和陆地重力都可以获得μGal级的时变重力信号,但是能用于研究的场源问题是有区别的。如果研究大范围陆面场源物质的运移问题,卫星重力观测高度可能占有一定优势。但是,如果研究地壳深部介质的场源参数,陆地重力测量优势十分明显。
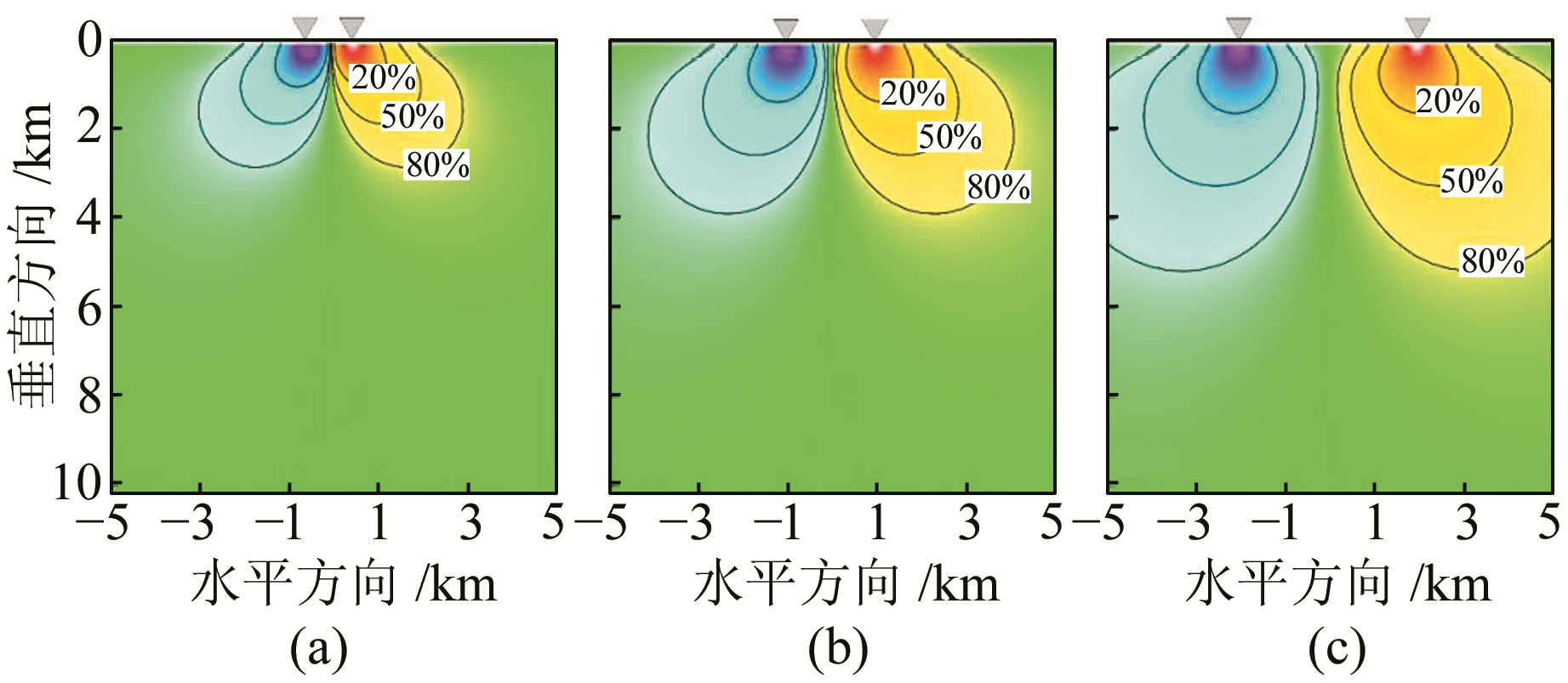
其次,分析不同水平距离对重力观测的场源敏感性。对不同的水平距离,通过观测两者之间的重力段差来计算其场源敏感性,如图 4所示。为了便于理解,图中模型单位采用km,但根据不同目的图中的单位适用于等比例缩放,如坐标单位统一变为m,敏感度计算结果不变。图 4(a)~4(c)分别给出了相距1 km、2 km和3 km的重力段差敏感度特征。结果显示,随着观测间距的加大,场源敏感区范围逐渐由浅源向深源方向增加。
|
图 4 不同水平间距时重力段差信号的场源敏感性分析 Fig. 4 The sensitivity analysis of field source for the different horizontal observed positions |
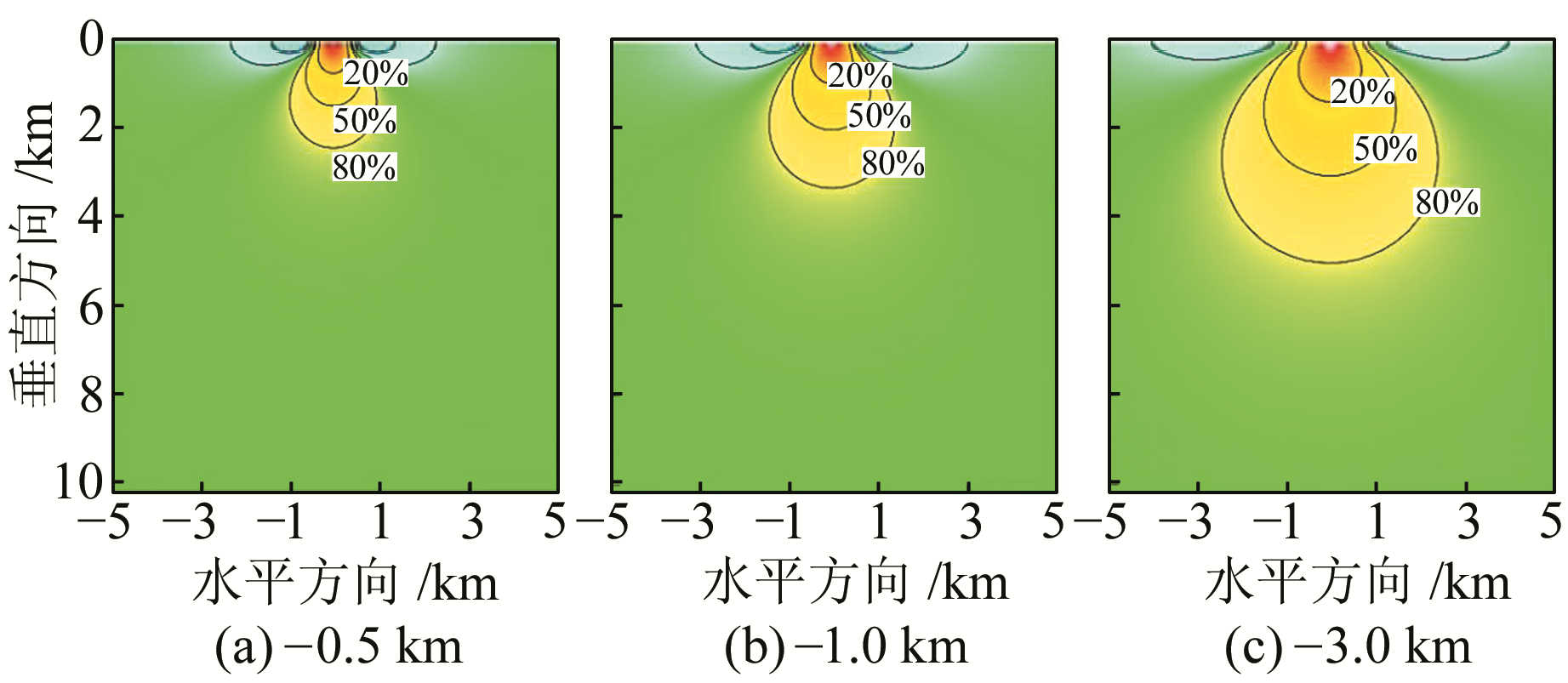
最后,计算不同垂直距离时的重力观测场源敏感性。做法同上,结果如图 5所示。与水平重力观测不同的是,垂直观测敏感区主要集中于观测点下方,但水平方向容易受浅部场源体的干扰。根据图 5(a)~5(c)所示的敏感性特征,测量不同高度的重力段差,较适合于研究浅层场源参数问题。
|
图 5 不同垂直高度的重力段差信号敏感度分析 Fig. 5 The sensitivity analysis of field source for the vertical gravity differences |
通过以上3个模型,分别对不同观测高度、水平段差、垂直段差的重力场源敏感性进行分析。这3类简单模型的计算结果对于认识观测系统的特性具有一定的指导意义,但现实情况下场源参数更加复杂,需要根据具体问题构建概念模型进行计算与分析,从而得到预期场源参数的重力信号特征,并辅助进行异常判断和信号分离。图 1(b)模型是基于叠加方法给出的场源敏感度结果,更适用于压制浅层干扰、分离出深部场源信号;而图 4、5给出的重力段差或梯度方法,则更适于分析浅源重力信号,压制深部场源的重力效应。
4 结语本文根据变基线重力梯度方法,提出一种“阵列式场地微重力观测系统”,并通过场源敏感度分析方法,利用多种模型计算给出了多种组合重力观测方式的潜在优势,其目的是让陆地重力观测能更加聚焦潜在的发震构造位置和深部介质场源信号。本文给出的重力场源敏感性分析方法也可以用于分析当前地震重力监测网络在各个地区的实际监测能力。
本文设计的阵列式重力观测系统,优点在于可以通过调整地表重力观测点之间的形态和布局来识别不同深度的场源信号。在实际工作中,场源敏感性分析方法可以帮助我们认识观测系统的探测能力,但还需要考虑各种观测本身的误差。当观测误差不足以识别潜在的场源信号时,需要及时改变观测系统的测量方式来优化观测系统。
本文设计的阵列式重力观测系统已经在北京国家地球观象台建成并进行实验性观测,相关研究结果可为研究深部地壳介质变形和可靠地震前兆提供具有重要科学意义的基础观测资料。
| [1] |
王谦身, 张赤军, 周文虎, 等. 微重力测量——理论、方法与应用[M]. 北京: 科学出版社, 1995 (Wang Qianshen, Zhang Chijun, Zhou Wenhu, et al. Microgravimetry-Theory, Method and Application[M]. Beijing: Science Press, 1995)
(  0) 0) |
| [2] |
Ferguson J F, Chen T, Brady J, et al. The 4D Microgravity Method for Waterflood Surveillance: Part Ⅱ-Gravity Measurements for the Prudhoe Bay Reservoir, Alaska[J]. Geophysics, 2007, 72(2): 133-143
(  0) 0) |
| [3] |
Ferguson J F, Klopping F J, Chen T, et al. The 4D Microgravity Method for Waterflood Surveillance: Part Ⅲ-4 D Absolute Microgravity Surveys at Prudhoe Bay, Alaska[J]. Geophysics, 2008, 73(6): 163-171 DOI:10.1190/1.2992510
(  0) 0) |
| [4] |
Hasan S, Troch P A, Bogaart P W, et al. Evaluating Catchment-Scale Hydrological Modeling by Means of Terrestrial Gravity Observations[J]. Water Resources Res, 2008, 44(8)
(  0) 0) |
| [5] |
郑秋月, 陈石. 应用GRACE卫星重力数据计算陆地水变化的相关进展评述[J]. 地球物理学进展, 2015, 30(6): 2603-2615 (Zheng Qiuyue, Chen Shi. Review on the Recent Development of Terrestrial Water Variations Using GRACE Satellite-Based Datum[J]. Progress in Geophysics, 2015, 30(6): 2603-2615 DOI:10.6038/pg20150619)
(  0) 0) |
| [6] |
Kuo J T, Sun Y F. Modeling Gravity Variations Caused by Dilatancies[J]. Tectonophysics, 1993, 227(1-4): 127-143 DOI:10.1016/0040-1951(93)90091-W
(  0) 0) |
| [7] |
Chen S, Jiang C, Zhuang J. Statistical Evaluation of Efficiency and Possibility of Earthquake Predictions with Gravity Field Variations and Its Analytic Signal in Western China[J]. Pure and Applied Geophysics, 2016, 173(1): 305-319 DOI:10.1007/s00024-015-1114-x
(  0) 0) |
| [8] |
Chen S, Liu M, Xing L L, et al. Gravity Increase before the 2015 MW7. 8 Nepal Earthquake[J]. Geophysical Research Letters, 43(1): 111-117 http://adsabs.harvard.edu/abs/2016GeoRL..43..111C
(  0) 0) |
| [9] |
顾功叙, 郭宗汾, 刘克人, 等. 中国京津唐张地区时间上连续的重力变化与地震的孕育和发生[J]. 科学通报, 1997, 42(18): 1920-1930 (Gu Gongxu, Kuo J T, Liu Keren, et al. Seismogenesis and Occurrence of Earthquake as Observed by Temporally Continuous Gravity Variation in China[J]. Chinese Science Bulletin, 1997, 42(18): 1920-1930)
(  0) 0) |
| [10] |
徐伟民, 陈石, 石磊. 新疆于田及周边地区地震活动性与重力异常特征[J]. 地球科学——中国地质大学学报, 2014, 39(12): 1831-1841 (Xu Weimin, Chen Shi, Shi Lei. Seismic Activity and Gravity Anomaly Characteristics of Yutian in Xinjiang and Surrounding Regions[J]. Earth Science-Journal of China University of Geosciences, 2014, 39(12): 1831-1841)
(  0) 0) |
| [11] |
Kenndy J, Ferre T P A, Guntner A, et al. Direct Measurement of Subsurface Mass Change Using the Variable Baseline Gravity Gradient Method[J]. Geophysical Research Letters, 2014, 41(8): 2827-2834 DOI:10.1002/2014GL059673
(  0) 0) |
2. Resource and Environmental Engineering College, Guizhou University, Huaxi District, Guiyang 550025, China
 2018, Vol. 38
2018, Vol. 38

