2. 武汉大学测绘学院,武汉市珞喻路129号,430079;
3. 苏州建设交通高等职业技术学校建筑工程系,苏州市吴中大道,215104
北冰洋表面的2/3被海冰所覆盖,这些海冰对北极地区的气候具有决定性的影响[1]。海冰出水高度的确定不仅是海冰研究的一个主要方面,也是北冰洋海面高、海面动力地形等海洋学研究的最大阻碍。尽管利用卫星遥感影像对海冰覆盖面积的监测已经持续了将近40 a,但由于技术条件的限制,海冰出水高度及厚度的反演一直是个难题。ICESat (ice, cloud, and land elevation satellite)激光测高卫星的出现改变了这一现状,其激光光波具有光斑小、不穿透雪层的特点,轨道覆盖的纬度范围达到±86°,为两极冰雪变化的研究提供了丰富、可靠的数据。2004年,Kwok等[2]首次论证利用ICESat数据确定海冰出水高度的可行性;此后几年,不同学者先后利用ICESat数据进行了确定两极海冰出水高度及厚度的研究[1, 3-8];文献[9-10]利用类似技术对海冰和海面数据进行分离,从而对北冰洋平均海面高及海面动力地形进行研究。在国内的研究中,范春波[11]探讨了联合重力数据和ICESat数据获取海冰出水高度的可能性; 邬晓冬[12]利用ICESat数据反演了南极罗斯海的海冰厚度; Bi等[13]利用ICESat数据获得的海冰出水高度对北冰洋海冰厚度变化进行了研究; 陈国栋等[14]对2005~2006年北冰洋海冰出水高度进行了分析。
本文利用2003-10~2008-03秋(10~11月)、冬(2~4月)2个季节共10期ICESat数据对北冰洋海冰出水高度的变化趋势进行研究,并对利用ICESat数据获取海冰出水高度过程中可能存在的系统误差进行分析。
1 数据描述及编辑ICESat卫星由美国国家航天局(NASA)于2003-01在戈达德航天中心发射升空,是全球首颗绕地飞行的激光测高卫星,其轨道倾角为94°,飞行高度约600 km,搭载的主要观测仪器为地学激光测高系统GLAS(geoscience laser altimeter system),采样率为40 Hz,其主要任务是研究两极地区冰雪的变化。由于设计缺陷,GLAS的第1个激光器在观测了37 d后损坏,且另外2个激光器可能存在同样的缺陷,因此ICESat观测任务由原计划的全年连续观测改为每年2~3个任务期、每期连续观测约33 d,轨道重复周期为91 d。最终,GLAS的3个激光器于2009-09全部损坏。6.5 a时间内ICESat共传回18期观测数据,根据使用的激光器编号及观测时间顺序,18个任务期被命名为L1、L2a~L2f以及L3a~L3k。
ICESat数据由美国冰雪数据中心(NSIDC)发布,共分为15种数据,本文使用的是Level 2海冰观测数据GLA13。在18期观测数据中,第1期观测(L1)由于采用了重复周期为8 d的试运行轨道造成地面轨迹间距过大,夏季的3期(L2c、L3c、L3f))以及2008-10以后的4期观测(L3k、L2d、L2e、L2f)则分别由于严重的大气散射和激光器的能量衰减导致观测质量较差,因此本文仅选取2003-09~2008-03的5期秋季和5期冬季观测数据,这些任务期的相关信息如表 1所示。
|
|
表 1 研究使用的ICESat数据信息 Tab. 1 Summary of ICESat data used in this research |
大气前向散射和波形饱和等误差会使ICESat测高数据产生cm级至m级的偏差[5]。为保证数据质量,本文对质量较差的数据进行剔除,主要编辑准则包括[4]:1)剔除反射率>1的数据;2)剔除接收回波拟合残差V>60的数据;3)剔除接收机增益大于30的数据;4)剔除反射率小于0.05以及波形展宽大于0.8 m的数据[5];5)由于本文的研究对象是海冰覆盖区域的海面,根据NSIDC发布的AMSR-E微波12.5 km分辨率的海冰覆盖率数据,剔除海冰覆盖率低于35%的区域[7]。
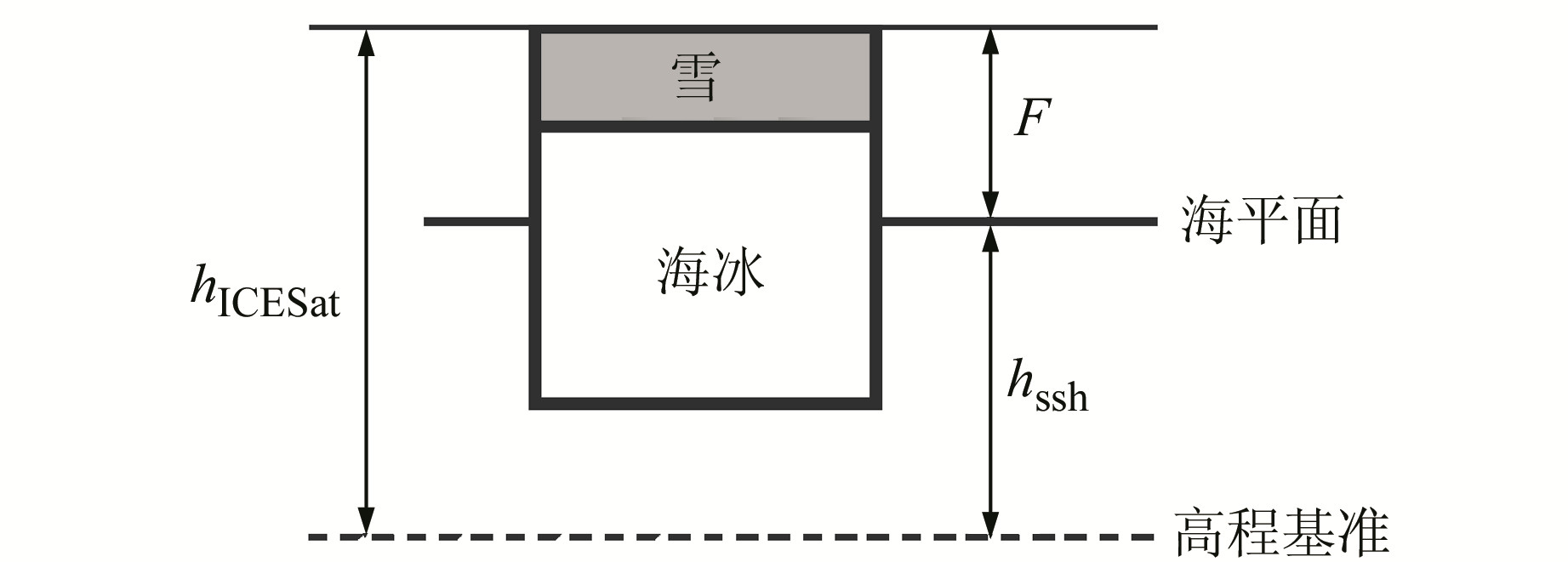
2 计算方法 2.1 ICESat高程预处理海冰出水高度(F)是指海冰露出海平面的高度。对于ICESat来说,由于激光无法穿透海冰表面的雪层,得到的出水高度是海冰露出海水的高度加上雪层的厚度(图 1)。故出水高度为ICESat测得的高度与海面高之差:
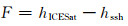
|
(1) |
|
图 1 ICESat海冰出水高度 Fig. 1 Illustration of ICESat freeboard |
目前,北冰洋海域没有可靠的平均海平面模型,因此要对ICESat高程进行预处理,尽量减少地球物理方面改正带来的影响。GLA13产品提供的测高数据中已经进行了潮汐和大气改正,因此ICESat高程观测值可表示为:
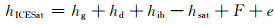
|
(2) |
式中,hg、hd、hib分别表示大地水准面、平均海面动力地形(mean dynamic topography,MDT)和逆气压改正,F为海冰出水高度,hsat为ICESat波形饱和改正,e为观测误差。选用的大地水准面模型为EGM2008,hsat在GLA13数据中已给出,hib由下式计算:
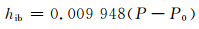
|
(3) |
式中,P0为标准大气压,P为GLA13给出的观测时的海面气压。将ICESat高程观测值加上MDT以外的各项改正后可得:
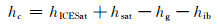
|
(4) |
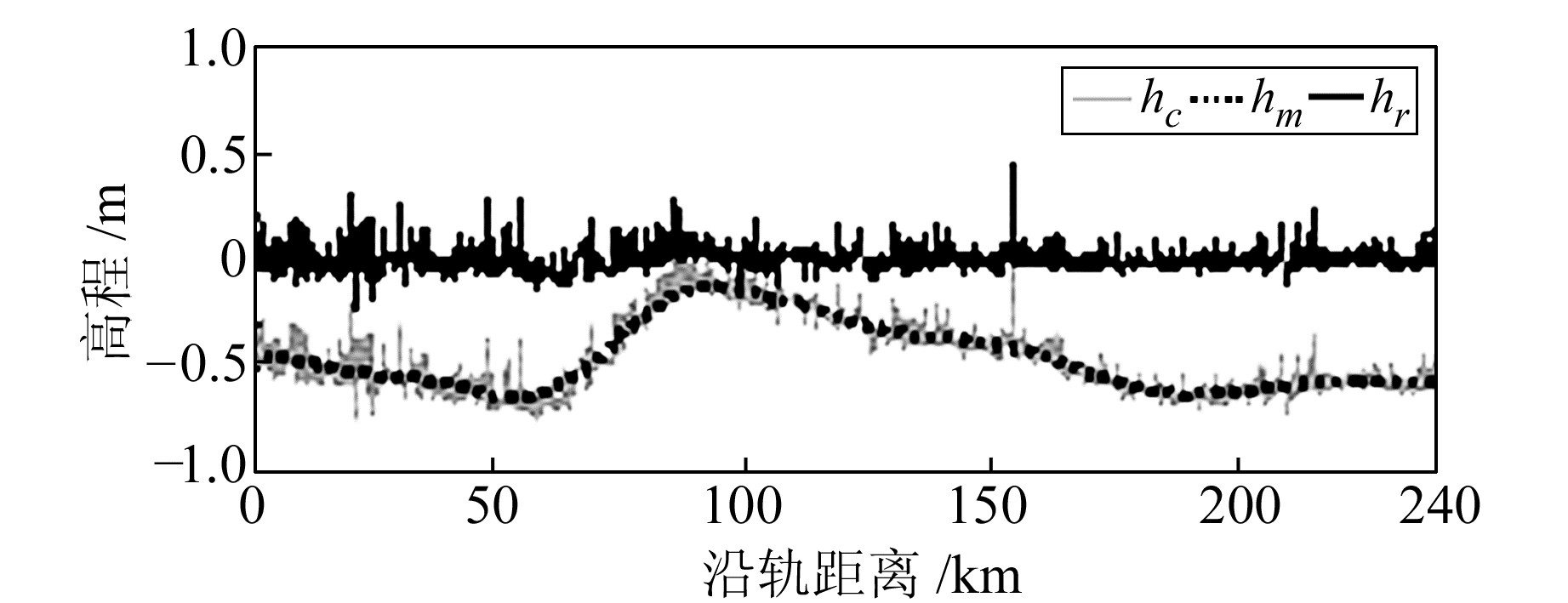
目前,北冰洋不同的MDT模型之间的差异较大[1],因此本文没有直接用模型来去除MDT的影响,而是将hc移去50 km移动平均值hm来获得一个零均值的高程序列hr(图 2),这可以有效地去除MDT以及大地水准面、潮汐等模型残差的长波部分。最后,获得的高程序列为:
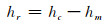
|
(5) |
|
图 2 ICESat高程序列 Fig. 2 ICESat derived elevation series |
式中,hm表示hc的50 km移动平均值。
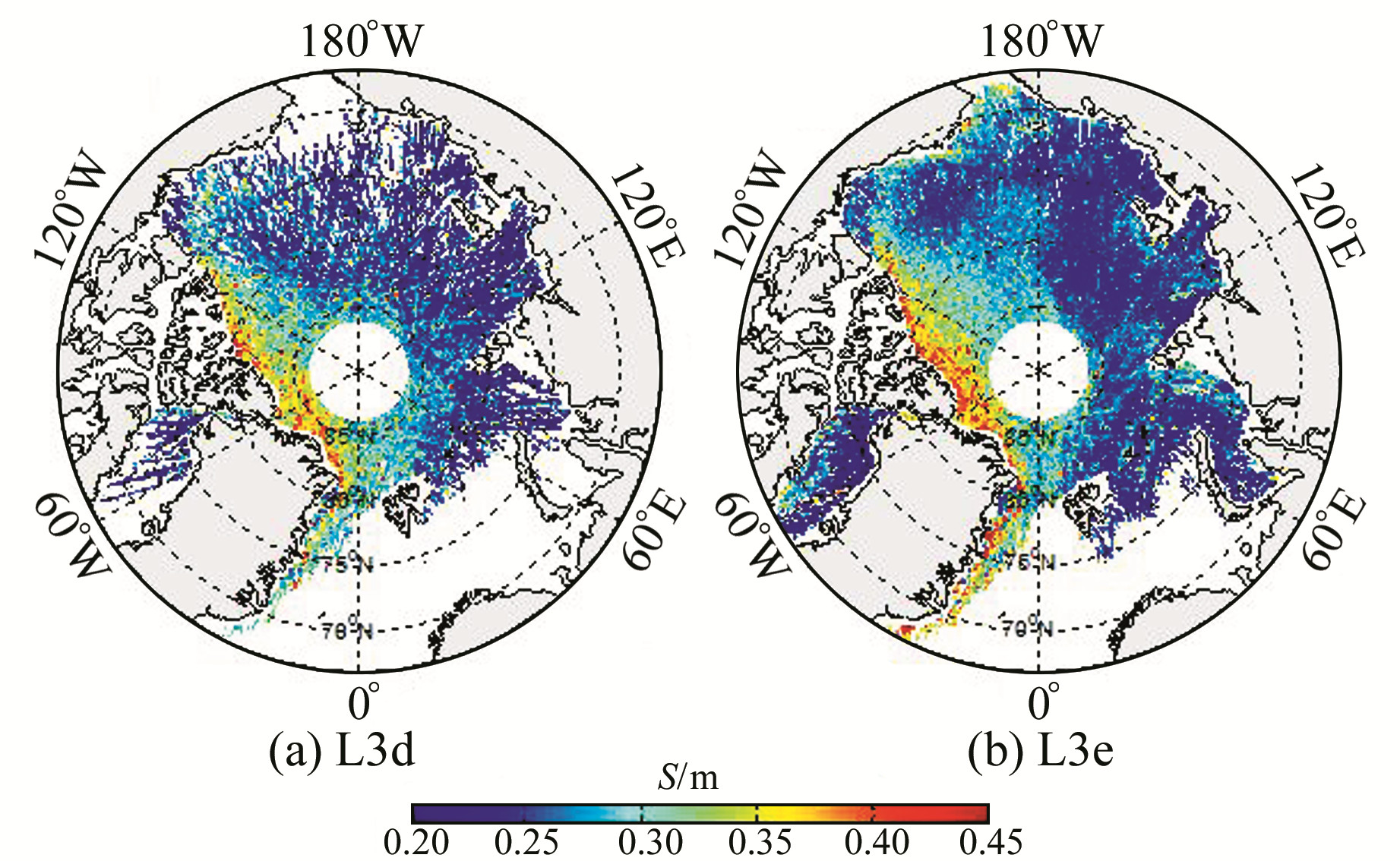
2.2 海冰出水高度的确定由于目前北极地区的地球物理模型精度不高,直接利用模型获得的北冰洋海面高并不准确,而在海冰水平运动的动力学效应下,海冰之间会产生一些巨大的裂缝,称为冰间水道(open lead),这些裂缝的宽度可达几百m至数km,利用ICESat在这些冰间水道上的观测值就可以确定海面高。选取ICESat海面观测数据的方法主要有2种,一种是在一定范围的沿轨数据中选取固定比例的最低点作为海面观测值,称为“最低面滤波法”[3];另一种则是根据ICESat回波的波形特征来识别来自海面的回波,称为“波形法”。Farrell等[7]采用这种方法确定了海冰出水高度。
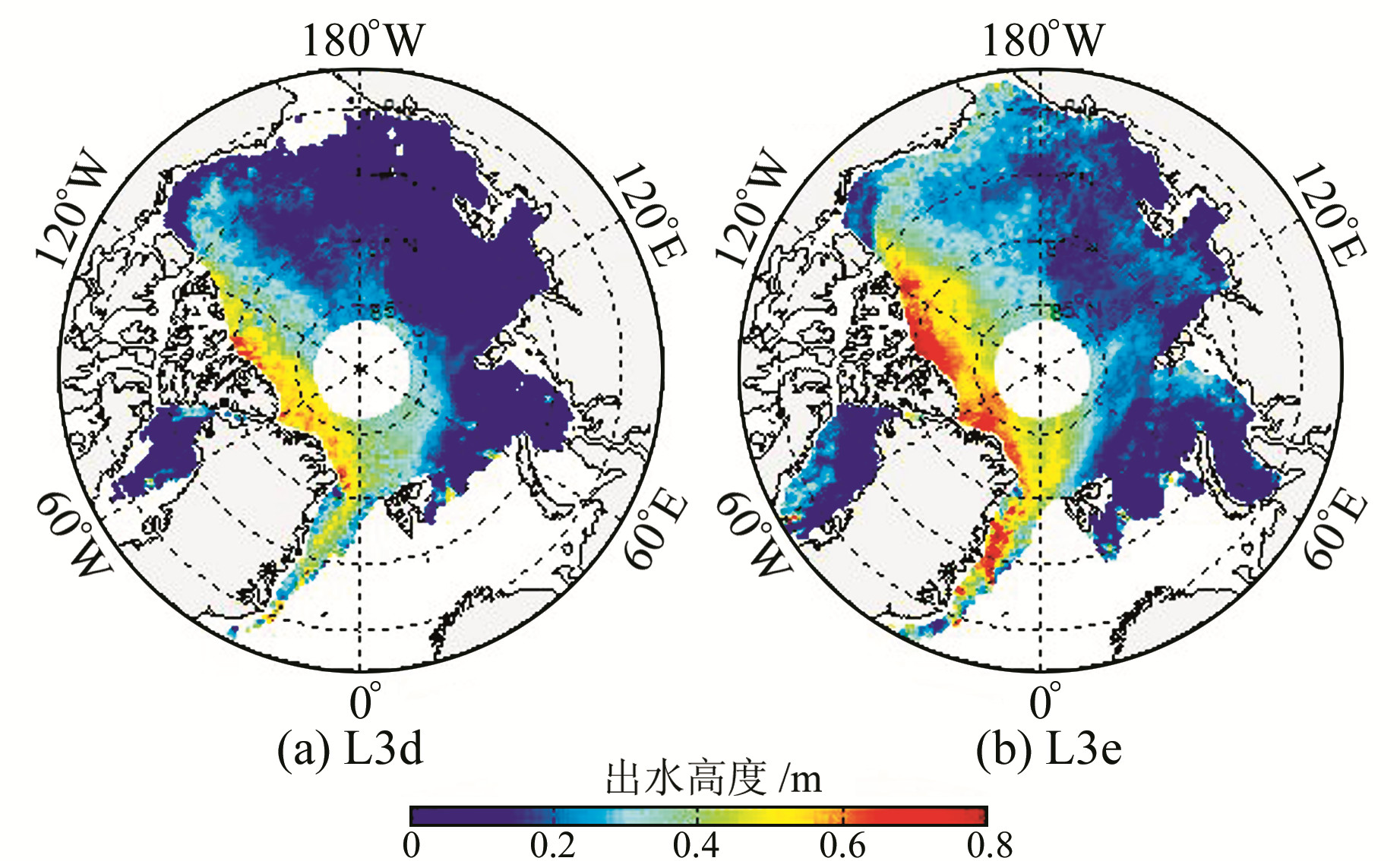
本文选择波形法进行海面观测值的识别,但Farrell等采用的方法需要使用GLA01的波形数据,计算比较复杂。本文根据卫星影像选取一些明显的ICESat在海面上的观测值,对这些点的回波波形参数进行分析,并确定识别海面观测值的波形特征条件[14]:波形反射率小于0.45、波形展宽小于0.3 m、脉冲信号长度小于5.25 m且回波拟合残差小于15。这些参数本身或者计算这些参数所需的数据都已在GLA13数据中给出,大大简化了计算。将ICESat沿轨数据分为25 km长的段,每个分段中识别出的海面观测值的平均值作为该段的海面高hssh,并由式(1)计算海冰出水高度。最后,将每一期的出水高度进行25 km×25 km的格网化。作为示例,图 3给出了L3d和L3e两期的出水高度格网,可以看出秋、冬两季出水高度的明显变化。
|
图 3 北极海冰出水高度分布 Fig. 3 Maps of Arctic freeboard |
本文选取的10个ICESat任务期的北冰洋平均海冰出水高度结果如图 4所示。作为对比,图中还给出了Skourup[6]、Renganathan[1]和NSIDC公布的出水高度结果,其中Renganathan采用根据大地水准面和海洋学模型确定海面高的方法,Skourup和NSIDC则采用最低面滤波法确定海面高,但在最低点的选取比例和范围等方面有所差异。本文结果与Skourup的结果在数值和变化趋势上都非常相似,平均差异为0.17 cm,最大差异仅为2.61 cm;与NSIDC的结果在季节变化方面具有较强的相似性,但存在明显的系统误差,两者的差异为6.6±1.9 cm。由于本文采用波形法确定海面高,因此在总体变化趋势上与NSIDC和Skourup的结果具有较高的相似性。

|
图 4 ICESat出水高度结果对比 Fig. 4 Comparison of ICESat derived freeboards |
相比之下,本文结果体现的季节性变化更一致,而其他2组结果都出现了同一年中秋季出水高度大于冬季出水高度的情况(2003-10~2004-10,2007-10~2008-03),这与其他大多数任务期体现的季节性变化相反,也违背北极海冰夏季消融、冬季增长的事实。这主要是由于波形法在海面观测数据的提取方面更严格,减小了海面高确定的误差,因而在上述几个卫星数据质量不佳的任务期取得了更为可靠的结果。Renganathan的结果与其他3组结果的差异都比较明显,特别是在出水高度的变化趋势上,看不出明显的年变化趋势,而其他3组结果则都表现出明显的下降趋势,这主要是由模型化的海面高不准确引起的。此外,Kwok等[4]和Farrell等[10]均只给出了L3d和L3e两期的平均出水高度结果,分别为27.5 cm、35.0 cm和25.4 cm、35.3 cm,而本文结果为27.5 cm和33.9 cm,三者结果非常接近。综上所述,本文结果与国外相关研究具有较高的一致性,与Renganathan结果的差异主要是由于计算方法不同而引起的,而与NSIDC的系统性误差将在后文详细讨论。
从图 5可以明显地看出,北冰洋海冰出水高度有逐年减少的趋势。对10期出水高度数据进行线性项和周年项拟合:
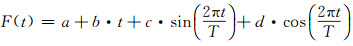
|
(6) |
|
图 5 北极海冰出水高度变化趋势 Fig. 5 Trends of Arctic sea ice freeboard |
式中,t表示时间,线性项参数b为海冰出水高度的年变化率。将出水高度数据代入拟合后得到-2.32 cm/a的线性年变化率以及6.32 cm的周年振幅。将秋、冬两季的出水高度分别进行线性拟合后,变化率分别为-2.23 cm/a和-2.32 cm/a,这个变化速率比Farrell等的结果(-1.8 cm/a和-1.6 cm/a)[7]要快。
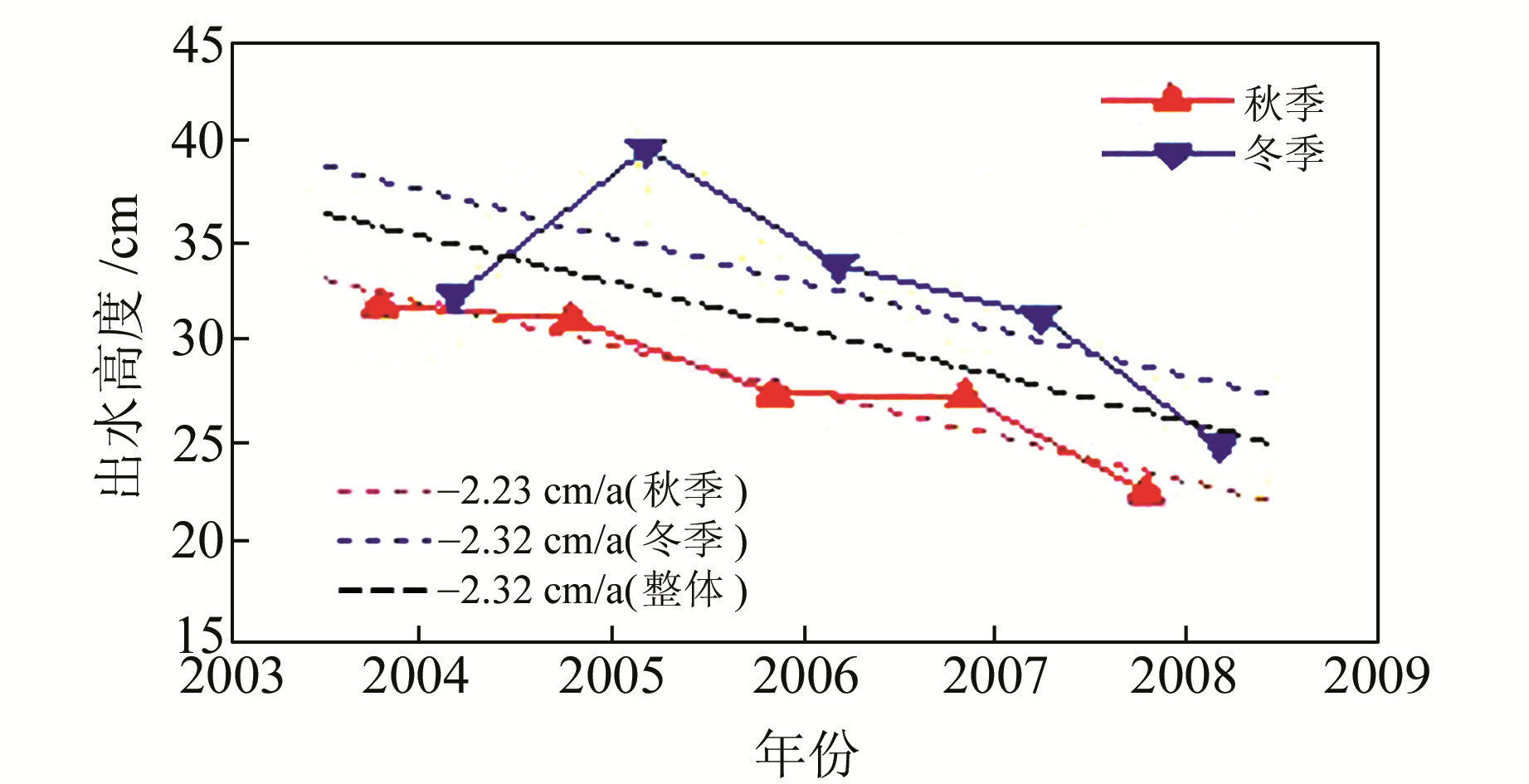
在利用ICESat确定北极海冰出水高度的过程中,我们发现一个有趣的现象:ICESat回波波形展宽S具有与海冰出水高度极其相似的分布。图 6为L3d、L3e两个任务期ICESat沿轨25 km内平均回波波形展宽的分布,数据统计表明,两者的相关性在2个任务期分别为0.66和0.61,这表示两者存在明显的内在关联。波形展宽S是指GLAS激光脉冲在经过反射面反射前后脉冲宽度的变化,在激光器系统的脉冲相对比较稳定的情况下,这个量主要由反射面的物理性质决定,反射面越粗糙,波形展宽越宽[15]。因此,S的大小代表GLAS激光光斑范围(直径约为55~70 m)内海冰表面的粗糙程度。Kwok等[4]的研究表明,ICESat沿轨25 km以内的平均海冰出水高度与这25 km内海冰表面高程起伏的标准差之间具有比较稳定的线性关系,这表示在几十km的大尺度范围内,海冰越厚的区域其表面高程的变化越大,根据浮力原理可知,海冰厚度的变化也越大。而S与出水高度的关系则表明,即使在小尺度范围内(100 m以内),海冰的变化也符合这一特征。
|
图 6 ICESat波形展宽分布 Fig. 6 ICESat pulse broadening |
在图 4的对比中,NSIDC与本文以及Skourup的结果之间存在明显的系统误差,特别是与Skourup的结果,由于同样采用最低面滤波法进行海面高的确定,因此两者的变化趋势几乎完全一致,平均差异为6.7±1.1 cm;而本文由于采用波形法,部分任务期的出水高度结果并没有与其他2组结果表现出特别明显的系统性差异,如L2b、L3b和L3j等。经过对比发现,3组结果在处理方法上的区别主要有:1)Skourup只对ICESat测高数据进行大地水准面、潮汐和逆气压改正,没有进行MDT改正,而NSIDC和本文都通过高通滤波(滑动平均处理)的方式去除MDT以及模型残差的长波影响,滤波窗口长度均为50 km;2)NSIDC根据沿轨每100 km范围内的海面观测值计算平均海面高,而Skourup和本文计算海面高的范围分别为20 km和25 km;3)NSIDC和Skourup在选取最低点时分别采用1%和2.5%的比例,而波形法则不需要选取最低点。为简洁起见,后文用dm表示高程滤波(滑动平均)的窗口长度,ds表示计算平均海面高的沿轨长度,p表示最低面滤波法中选取最低点的比例。
高程滤波的主要目的是消除MDT和模型残差的影响,但滤波过程也有可能会消除海冰出水高度随空间变化的信号,从而使计算的出水高度出现系统性误差。此外,对于最低面滤波法,高程滤波还会产生额外的系统误差,因为在选取最低点时总会倾向于找到MDT最低和模型误差最大的点,也就是说,高程序列中MDT和模型残差量级越大,最低点法确定的海平面就越低,出水高度的结果就会越大。而对于波形法则不会有这种额外的误差,因为波形法选取的海面观测值受到的MDT和模型残差的影响是随机的,在整个海冰覆盖区域的数十万个数据取平均后,这种模型误差可以忽略不计。
本文设计一个实验来定量地确定dm对出水高度计算的影响。利用波形法在长度为ds的沿轨数据中选取一定数量的海面观测值,这些观测值在滤波前的平均高程确定的海面高为ssho;根据滤波后的高程序列确定出水高度后,可以根据式(1)再计算一个海面高sshc。显然ssho与sshc应该相等,不等则表明出水高度的计算产生了误差。因此,可以用sshc-ssho定量确定出水高度的计算是否存在误差。利用L3d和L3e两个不同季节的数据,分别计算不同的dm和ds所对应的出水高度平均误差,结果如图 7所示。所有的结果均为正,这表示sshc偏高,即出水高度的结果偏小,这印证了前文所述的出水高度信号可能会在滤波过程中被消除的观点;dm越小,出水高度误差越大,这是因为有更多的出水高度信号被消除掉了。在所有数据中,dm在50 km以下时,引起的出水高度计算结果差异较大;而在50 km以上时变化较小,这说明海冰出水高度变化的信号主要集中在50 km以下的波长,滤波时dm的选择至少要在50 km以上才能够充分保留海冰出水高度变化的特征。在dm和ds都相同的条件下,冬季(L3e)的出水高度误差始终大于秋季(L3d),这表明冬季海冰出水高度的变化更大,这也符合海冰越厚其表面高程变化越大的结论。我们还注意到,同等条件下,ds越大出水高度的误差越大,特别是秋季ds取100 km以及冬季ds取75 km、100 km时,即使进行100 km的滤波,仍然存在一定的误差,但量级仅为1~2 mm,而在其他情况下,dm大于70 km时误差几乎为0。实验结果表明,较小的ds计算出水高度的误差较小,但我们没有找到明确的证据来解释为什么ds的长度会对出水高度的计算产生这种影响,这有待进一步研究。

|
图 7 dm对海面高计算的影响 Fig. 7 Effect of ds value on sea surface height calculation |
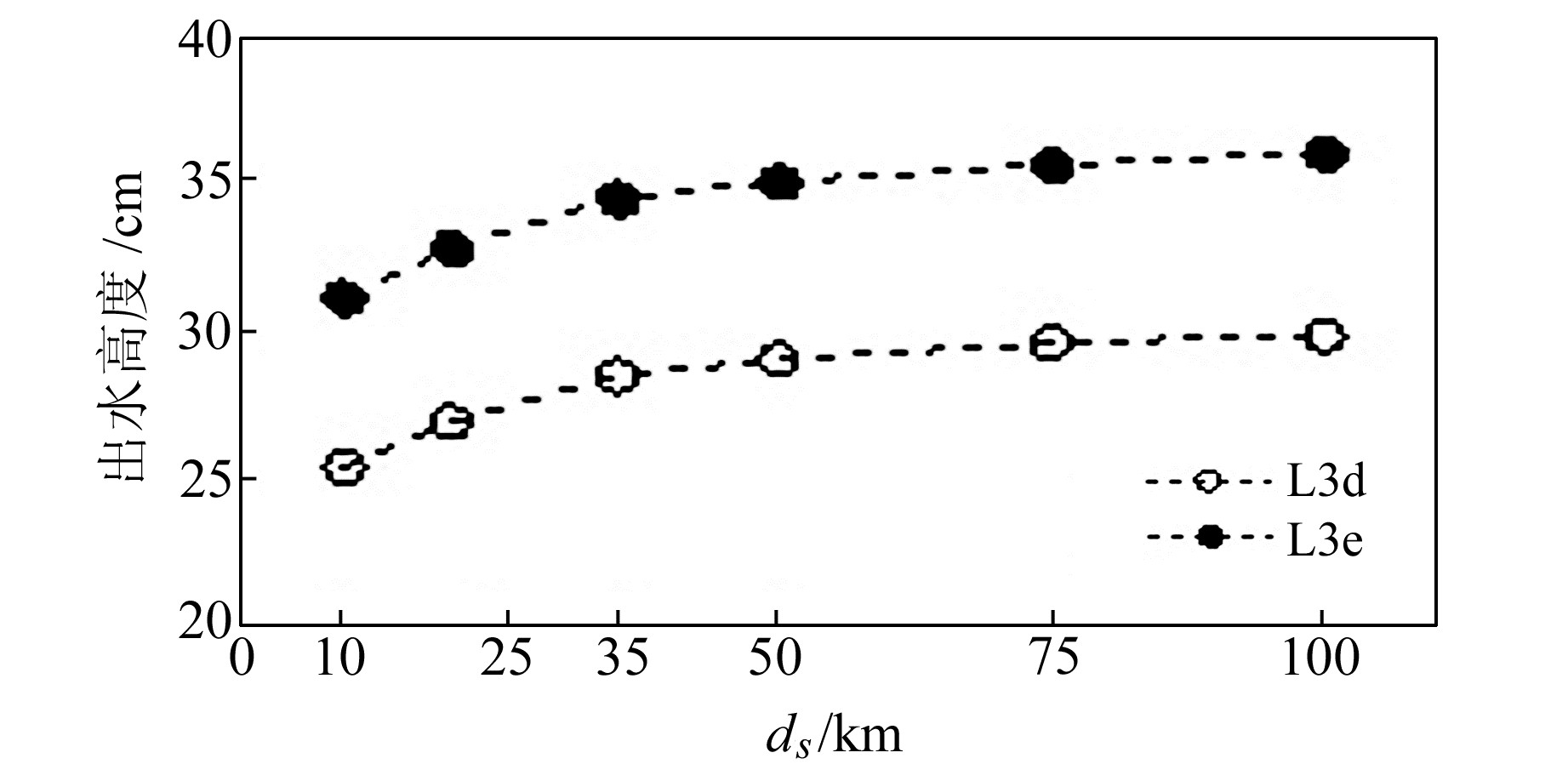
采用波形法时,ds仅对结果产生mm级的影响,但采用最低面滤波法时,ds的影响则要大得多。例如,一段沿轨数据原本以ds=25 km的搜索范围确定的海面高为H,当ds扩大为50 km时,如果新增的观测值中的点均高于H,那么重新选取最低点后,该段的海面高仍会被确定为H,但如果新增的观测值中有低于H的点,那么这些点会被选为海面观测值,因此最终确定的海面高会低于H,使得计算的出水高度大于原来dm=25 km时的结果。将dm和p分别固定为25 km和2.5%,利用最低面滤波法在不同的ds条件下计算L3d和L3e的出水高度,结果如图 8所示。不论在秋季还是冬季,ds取10 km和100 km时计算出水高度的差异都达到5 cm左右,而北冰洋平均出水高度仅为30 cm左右。
|
图 8 不同ds计算的出水高度 Fig. 8 Freeboards calculated with different ds value |
最低点比例p对于最低面滤波法是至关重要的参数,因为只有在p符合海冰之间露出的海水面(冰间水道)的实际比例时,才能够得到合理的海冰出水高度。如果p过高,则会在海面高的计算中引入海冰表面上的高程,使海面高偏高,从而使计算的出水高度偏小;反之,如果p过低,虽然降低了引入海冰高程的可能性,但可能引入较多的由ICESat测高误差(ICESat测高精度约为14 cm)引起的偏低的海平面数据,从而使最终的出水高度偏大。Skourup和NSIDC分别选取2.5%和1%的比例,在其他条件相同的情况下,经计算仅这一项引起的出水高度的差异约为3~4 cm。事实上,冰间水道的比例和分布并不均匀,现有资料表明,在不同区域、不同季节冰间水道的分布情况都不相同[16-17],因此在整个北极海域选取固定比例的最低点计算海面高并不是十分合理的方法。Skourup的结果与采用波形法的本文以及Farrell等[7]的结果在量级上比较接近,而NSIDC则相差较大,这表明2.5%的比例可能更接近北冰洋冰间水道的平均分布比例。
根据以上讨论,dm较为合适的取值为50 km,既可消除长波的地球物理模型误差,也最大限度地保留了海冰出水高度变化的信号。ds选取25 km,一方面是因为根据图 7的结果,较小的ds引起出水高度的计算误差较小,另一方面也是因为25 km尺度可减小ICESat空间分辨率对出水高度计算造成的影响[18]。
5 结语本文利用2003-10~2008-03 ICESat测高数据研究北极海冰出水高度的变化。结果显示,北冰洋的海冰厚度在这5 a中呈现出明显的下降趋势。北极海冰出水高度的年变化率为-2.32 cm/a,秋、冬2个季节的变化率分别为-2.23 cm/a和-2.32 cm/a。利用ICESat数据确定海冰出水高度的方法中存在系统误差,分析表明最低点比例p、滑动平均窗口长度dm和海面高搜索范围ds的选取都会对出水高度的计算结果产生cm级的系统误差。通过对比实验,dm和ds分别选取50 km和25 km时对出水高度的计算最合适,而最低点比例的选取则有待于对冰间水道分布的进一步研究。
| [1] |
Renganathan V. Arctic Sea Ice Freeboard Heights from Satellite Altimetry[D]. Calgary: University of Calgary, 2010 http://adsabs.harvard.edu/abs/2010PhDT........40R
(  0) 0) |
| [2] |
Kwok R, Zwally H J, Yi D. ICESat Observations of Arctic Sea Ice: A First Look[J]. Geophysical Research Letters, 2004, 31(16)
(  0) 0) |
| [3] |
Forsberg R, Skourup H. Arctic Ocean Gravity, Geoid and Sea-Ice Freeboard Heights from ICESat and GRACE[J]. Geophysical Research Letters, 2005, 32(21)
(  0) 0) |
| [4] |
Kwok R, Cunningham G F, Zwally H J, et al. Ice, Cloud, and Land Elevation Satellite (ICESat) over Arctic Sea Ice:Retrieval of Freeboard[J]. Journal of Geophysical Research:Oceans, 2007, 112(C12)
(  0) 0) |
| [5] |
Zwally H J, Yi D, Kwok R, et al. ICESat Measurements of Sea Ice Freeboard and Estimates of Sea Ice Thickness in the Weddell Sea[J]. Journal of Geophysical Research:Oceans, 2008, 113(C2)
(  0) 0) |
| [6] |
Skourup H, A Study of Arctic Sea Ice Freeboard Heights, Gravity Anomalies and Dynamic Topography from ICESat Measurements[D]. Copenhagen: University of Copenhagen, 2009
(  0) 0) |
| [7] |
Farrell S L, Laxon S W, McAdoo D C, et al. Five Years of Arctic Sea Ice Freeboard Measurements from the Ice, Cloud and Land Elevation Satellite[J]. Journal of Geophysical Research:Oceans, 2009, 114(C4)
(  0) 0) |
| [8] |
Xie H, Tekeli A E, Ackley S F, et al. Sea Ice Thickness Estimations from ICESat Altimetry over the Bellingshausen and Amundsen Seas, 2003-2009[J]. Journal of Geophysical Research :Oceans, 2013, 118(5): 2-2 453
(  0) 0) |
| [9] |
Kwok R, Morison J. Dynamic Topography of the Ice-Covered Arctic Ocean from ICESat[J]. Geophysical Research Letters, 2011, 38(2)
(  0) 0) |
| [10] |
Farrell S L, McAdoo D C, Laxon S W, et al. Mean Dynamic Topography of the Arctic Ocean[J]. Geophysical Research Letters, 2012, 39(1)
(  0) 0) |
| [11] |
范春波. 星载激光测高理论与应用[D]. 武汉: 武汉大学, 2007 (Fan Chunbo. Theory and Application of Spaceborne Laser Altimeter[D]. Wuhan: Wuhan University, 2007)
(  0) 0) |
| [12] |
邬晓冬. 南极罗斯海海冰厚度和面积变化研究[D]. 青岛: 中国海洋大学, 2012 (Wu Xiaodong. Variation of Sea Ice Thickness and Area in the Ross Sea[D]. Qingdao: Ocean University of China, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10423-1012505200.htm
(  0) 0) |
| [13] |
Bi H B, Huang H J, Su Q, et al. An Arctic Sea Ice Thickness Variability Revealed from Satellite Altimetric Measurements[J]. Acta Oceanologica Sinica, 2014, 33(11): 134-140 DOI:10.1007/s13131-014-0562-y
(  0) 0) |
| [14] |
陈国栋, 李建成, 褚永海, 等. 利用ICESat数据确定北冰洋海冰出水高度:以2005~2006年为例[J]. 测绘学报, 2015, 44(6): 625-633 (Chen Guodong, Li Jiancheng, Chu Yonghai, et al. Determination of Sea Ice Freeboard in Arctic from ICESat, Case Study of 2005-2006[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 625-633)
(  0) 0) |
| [15] |
Brenner A C, Zwally H J, Bentley C R, et al. Geoscience Laser Altimeter System (GLAS) Algorithm Theoretical Basis Document[EB/OL]. http://www.csr.utexas.edu/glas/atbd.html, 2011-11
(  0) 0) |
| [16] |
Lindsay R W, Rothrock D A. Arctic Sea Ice Leads from Advanced Very High Resolution Radiometer Images[J]. Journal of Geophysical Research:Oceans, 1995, 100(C3): 4-4 544
(  0) 0) |
| [17] |
Laxon S, Peacock N, Smith D. High Interannual Variability of Sea Ice Thickness in the Arctic Region[J]. Nature, 2003, 425(6 961): 947-950
(  0) 0) |
| [18] |
Weissling B P, Ackley S F. Antarctic Sea-Ice Altimetry: Scale and Resolution Effects on Derived Ice Thickness Distribution[J]. Annals of Glaciology, 2011, 52(57): 225-232 DOI:10.3189/172756411795931679
(  0) 0) |
2. School of Geodesy and Geodetics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Department of Architecture and Engineering, Suzhou Institute of Construction and Communications, Wuzhong Road, Suzhou 215104, China
 2017, Vol. 37
2017, Vol. 37


