2011-03-11日本MW9.0地震是日本有地震记录以来震级最大的一次,其发生在太平洋板块俯冲到欧亚板块和北美板块的俯冲带上,属于海沟逆冲型巨大地震。GPS观测显示,此次地震造成巨大的同震变形,影响范围非常广泛[1-2],在距破裂带约150 km处观测到近场地表最大位移超过5 m,在中国大陆东北和华北地区的远场仍可观测到cm级的同震水平位移,最大值达35 mm。此次地震产生的震后形变非常大,不少学者利用GPS观测值对震后形变特征和机理开展了研究[3-5]。Diao等[3]用震后1.5 a的GPS数据,将震后余滑和粘弹性松弛相结合对震后地表形变进行解释,认为震后形变初期余滑起主要作用;王丽凤等[4]利用震后1 a的GPS数据研究认为,仅蠕滑在震后1 a所累积释放的能量就等效于一个8.7级地震,震后1 a观测到的形变基本上可由沿着断层面的蠕滑进行模拟,粘弹性松弛的贡献不大,地震造成的粘弹性松弛在未来50~100 a的尺度上,对中国东北地区有拉张效应。
对于震后形变机制问题,学者们进行了大量研究。Hsu等[6]认为震后形变主要由断层的震后余滑引起;Pollitz等[7]认为震后形变是由介质的粘弹性松弛所致;Jónsson等[8]认为震后形变是由孔隙流体调整导致。随着对震后过程研究的深入,学者们发现震后形变可能是由多种机制共同作用引起的[9]。日本地震产生的巨大同震和震后形变,为利用GPS等观测值研究大地震的形变特征和机制提供了难得的震例。
本文利用截至2015-12的GPS观测数据,研究日本MW9.0地震震后位移的变化规律;利用震后余滑和粘弹性位错理论模拟和解释该地震引起的震后形变,并估算该区域的粘滞性系数,为认识大地震变形的动力学机理和探索区域粘滞性结构增加科学认识和积累。
1 GPS数据处理本文采用由美国内华达州大地测量实验室发布的日本境内GPS连续站观测的位移变化数据,采用GIPSY/OASIS软件处理的IGS2008参考框架下的结果。在日本地震破裂面近垂直方向上选取8个观测时间相对较长且观测资料较完整的GPS连续站(表 1),对其进行数据处理,并研究其震后形变特征。
|
|
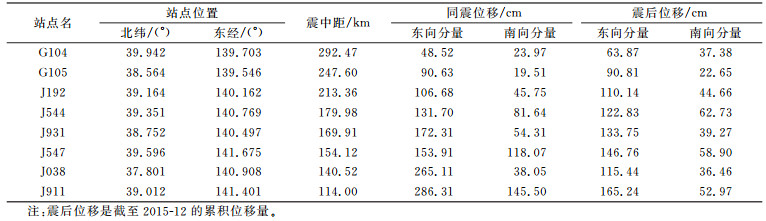
表 1 GPS观测的同震及震后位移 Tab. 1 Co- and post-seismic horizontal displacements observed by GPS |
相对于水平分量,GPS观测的垂直分量误差较大、信噪比较低,因此在震后形变研究中只采用水平分量的位移数据。利用最小二乘方法对震前观测数据进行线性趋势拟合,从位移时间序列中扣除该长趋势项,得到地震前后的水平位移变化。在此基础上,对震后位移时间序列扣除同震阶跃,得到各GPS台站观测的震后水平位移变化(图 2、3),各站点观测的同震及震后位移见表 1。从GPS位移时间序列的处理结果可以看到,日本本岛在日本MW9.0大地震后发生了显著的震后形变,在震后近5 a内东向地表水平位移量累积达到60~165 cm,而南向地表水平位移量累积达到20~65 cm,且地表水平位移量还在持续积累。在震中距超过210 km的G104、G105及J192站点所观测到的震后位移累积变化已超过同震位移。从结果中还可以明显地看到,震后地壳运动速率随时间呈衰减变化特征。
|
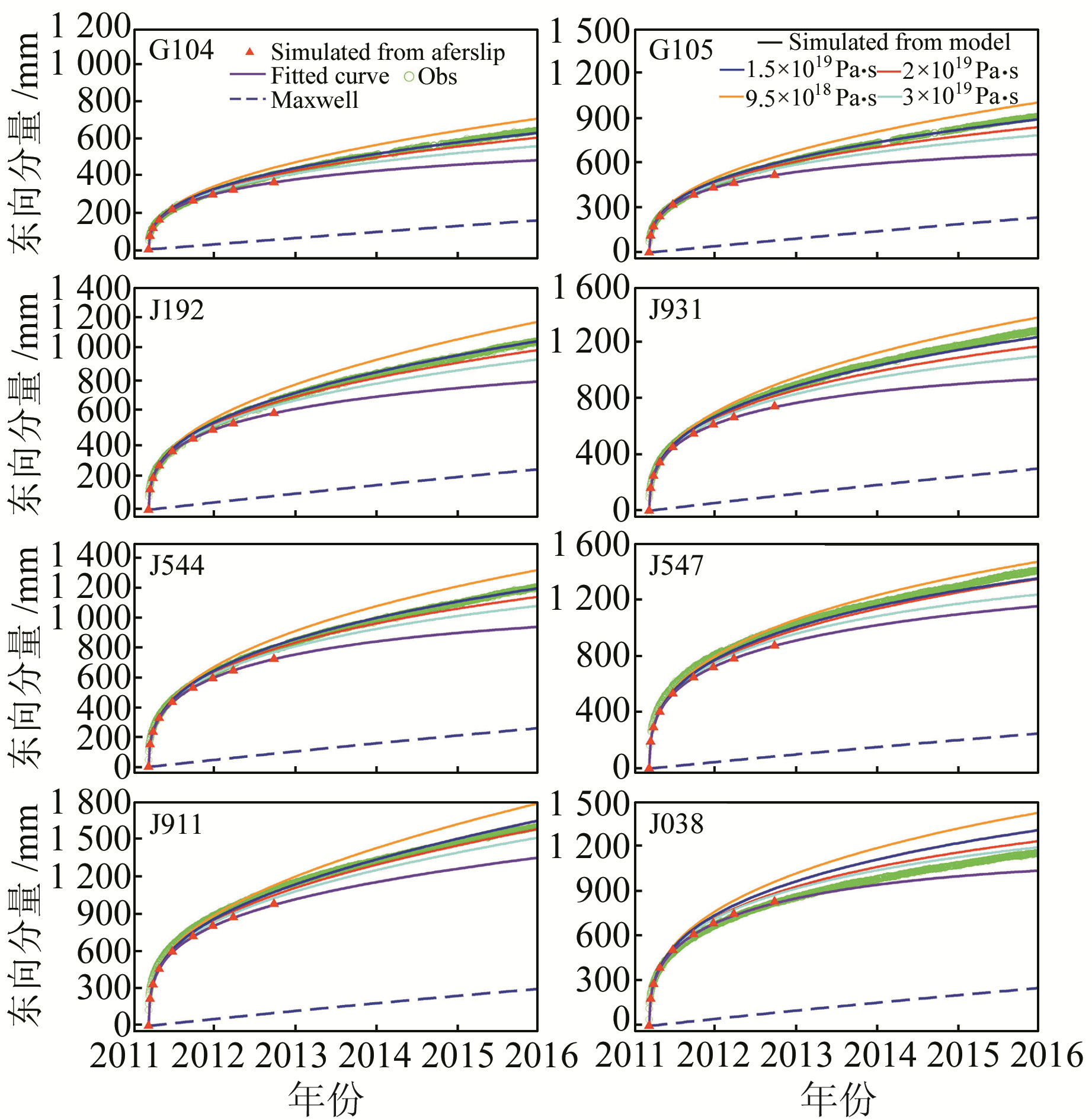
图 2 模拟的震后东向位移与GPS观测值的比较 Fig. 2 Comparisons between calculated and GPS observed east components of post-seismic displacements |
|
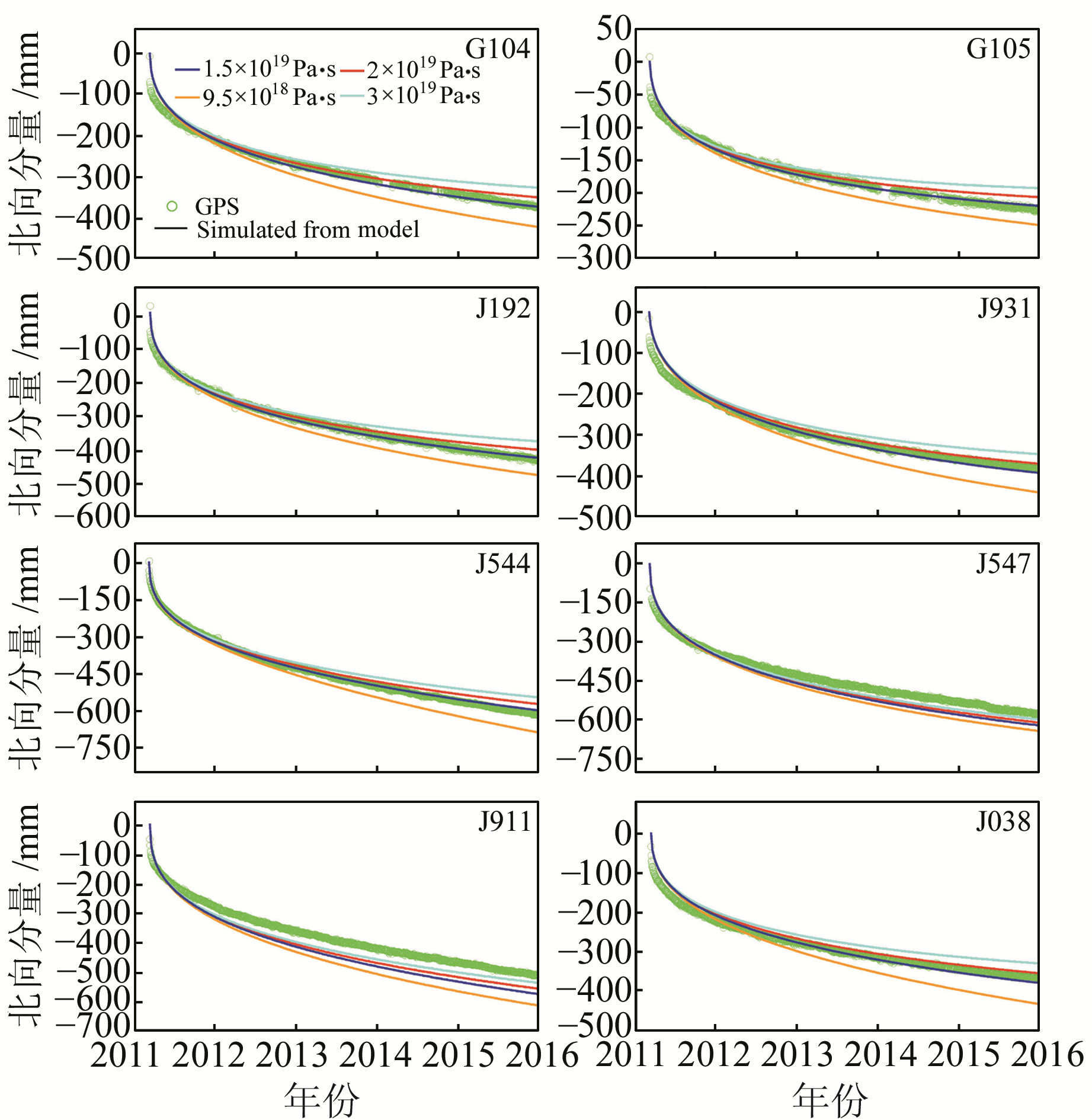
图 3 模拟的震后北向位移与GPS观测值的比较 Fig. 3 Comparisons between calculated and GPS observed north components of post-seismic displacements |
GPS观测显示,日本地震震后位移变化呈现出指数函数变化特征,这是震后余滑、粘滞性松弛等多种作用的结果。本文尝试利用粘弹性位错模拟和震后余滑相结合来认识和解释这种震后形变特征。利用Wang等[10]的PSGRN/PSCMP程序来模拟日本MW9.0地震的同震及震后形变。
2.1 断层滑动模型和地球介质模型日本地震后,学者们依据不同的观测数据给出了各自的断层滑动分布模型。Shao等[11]使用远震波形数据;Pollitz等[12]使用大地测量数据;Wei等[13]联合使用地震波形和大地测量数据。不同的断层滑动模型在滑移大小和地震矩上可能基本相同,但在滑动分布等细节上不尽相同。为准确解释观测数据,有必要在众多模型中选取一个最为合理的地震断层滑动模型。Wang等[14]的研究表明,Wei等[13]联合强震仪观测的地震波数据以及日本本岛GPS数据反演的地震断层滑动模型能较好地解释观测数据,因此在模拟研究中选择该地震断层滑动模型。
参考PREM模型[15]、Crust 2.0模型[16]和Diao等[3]的研究结果,构建地震区域的地球介质模型。将该地区的地球介质划分为6层,其中前3层为弹性层,其参数设置参考Crust 2.0模型,弹性层总厚度为40 km。后3层为粘滞层,分为40 ~220 km的软流圈部分和220 km以下的地幔部分,粘弹性介质采用Maxwell体。软流圈部分分为2层,粘滞性系数为参数η1;220 km以下的地幔部分的粘滞性系数设为参数η2,其余参数设置参考PREM模型。地球介质模型具体参数见表 2。
|
|
表 2 日本地震区域地球分层模型 Tab. 2 Earth layering model in the region of Japan earthquake |
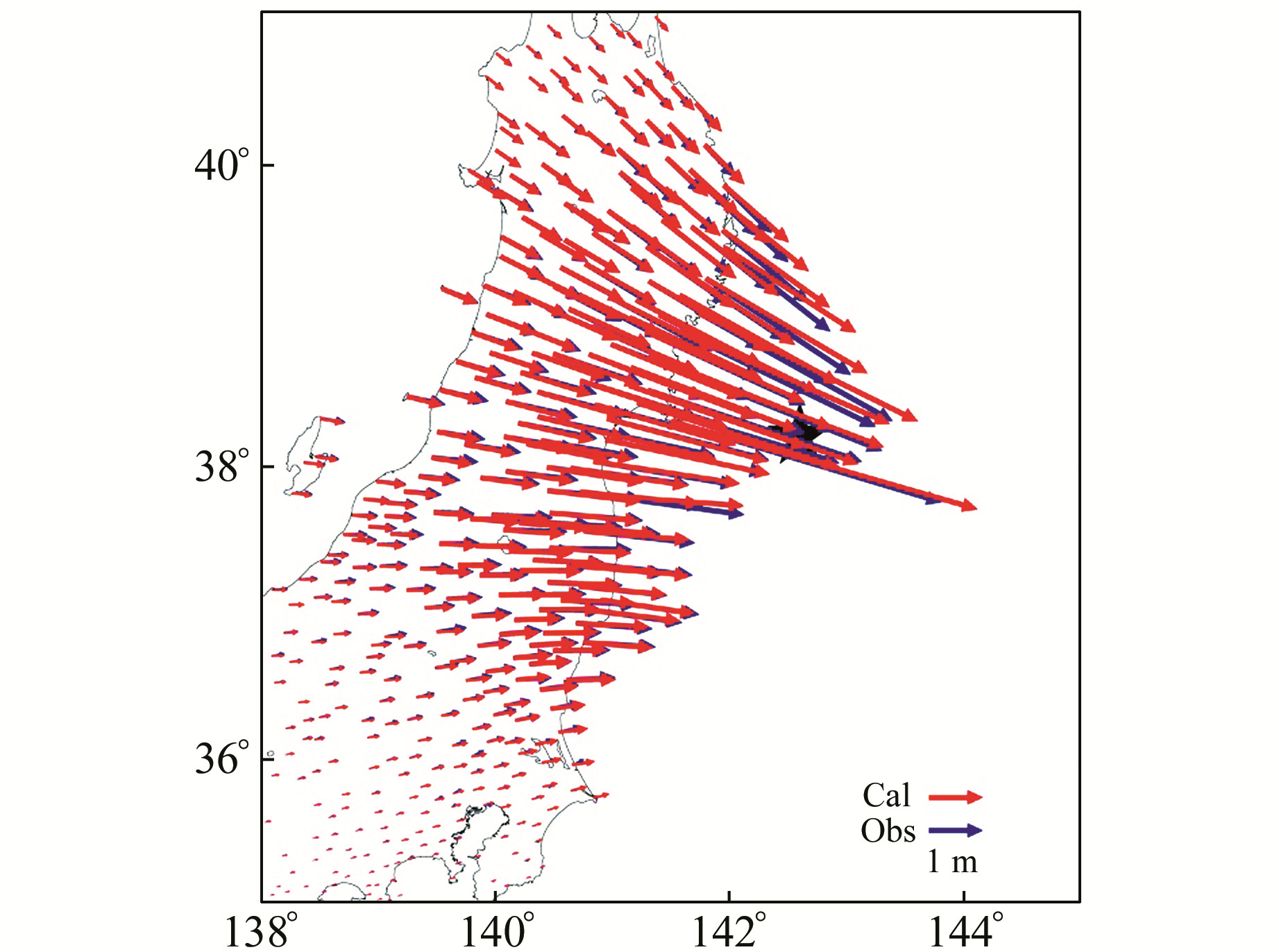
利用上述地震断层模型和地球分层模型,基于位错理论模拟计算此次日本地震的同震位移变化,并与ARIA团队解算的同震位移进行比较。图 1给出了两者比较的情况,可以看出,利用位错模型计算的模拟值无论是在空间分布还是在量级上都与观测值符合得非常一致。对于1 232个GPS观测点,计算模拟值与观测值之间的均方根(RMS)误差,以此定量判断二者的符合程度。计算结果显示,两者之间的RMS值约为4.8 cm,优于Zhou等[17]位错模型模拟值与相同GPS观测值间的偏差。模拟值与观测值符合较好,这反映了选取和构建的模型可以比较合理地解释GPS同震位移。在此基础上,利用粘弹性位错理论来模拟和解释GPS观测的震后形变。
|
图 1 日本地震同震水平位移 Fig. 1 Coseismic horizontal displacements of the Japan earthquake |
利用粘弹性分层模型,模拟计算8个GPS连续站由震后粘滞性松弛引起的位移变化。参考文献[3]和[7],把参数η2的值设为1×1020 Pa ·s,分析参数η1的变化。将模拟的震后位移与观测值比较,图 2(绿色圆圈代表GPS观测值,蓝色虚线代表由粘滞性松弛引起的震后位移变化,红色三角形是利用震后余滑模型计算的震后位移变化,紫色实线为修正后Omori公式对震后余滑引起位移数据的拟合结果,其他实线是综合震后余滑和粘滞性松弛作用的结果。不同颜色为不同粘滞系数的模拟值,橙色曲线η为9.5×1018 Pa ·s,蓝色曲线η为1.5×1019 Pa ·s,红色曲线η为2×1019 Pa ·s,青色曲线η为3×1019 Pa ·s)给出了两者比较的情况,其中η1为1.5×1019 Pa ·s。可以看出,模拟值与观测值并不符合,且相差非常大,当η1发生变化时,这种差异仍然存在,说明震后形变并不仅由粘滞性松弛引起,而是由多种机制共同作用的结果。目前普遍认为,震后形变主要由断层的震后余滑、介质的粘弹性松弛以及孔隙流体调整等引起。因此,除上述粘滞性松弛外,还需要考虑由震后余滑等造成的位移变化。
利用Diao等[3]反演的震后余滑模型(Model 2)和上述构建的地球介质模型模拟震后余滑引起的位移变化(图 2中红色三角形)。由于Diao等[3]反演的震后余滑模型只反映震后约1.5 a内的位移变化,不满足本文所模拟计算的时间尺度,因此对该数据利用修正后的Omori公式[5]进行拟合,即对震后余滑引起的震后位移时间序列进行拟合:
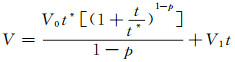
|
(1) |
式中,V为震后位移,t为距发震时刻的时间间隔,t*、V0、V1和p为要拟合的参数,t*为特征时间,V0为初始值,V1为恒定的变化率,p为位移衰减速率。
图 2中的紫色实线是表 1所给出的8个GPS连续站,利用式(1)拟合得到的由震后余滑引起的位移变化。可以看出,该函数可以很好地拟合由震后余滑作用引起的震后1.5 a的位移变化,且外推了1.5 a之后的位移变化情况。同时也可以看出,震后余滑作用造成的位移变化符合指数函数的时间衰减特性。与GPS观测值相比较可以发现,在震后几个月内震后余滑引起的地表位移与观测值相符甚好,说明在震后形变初期震后余滑起主要作用,控制着震源及周边区域的变形,但随着时间的增长,其与观测值偏差越来越大,说明在震后形变后期余滑作用逐渐减弱。
通过对震后余滑以及粘弹性松弛作用引起的位移变化模拟发现,在震后短时间尺度内考虑震后余滑作用可以较好地解释日本MW9.0地震的震后形变,但对于长时间尺度的震后形变,仅考虑震后余滑作用或粘弹性松弛作用并不能合理地解释GPS观测的形变。因此,需要综合考虑二者的影响。将上述震后余滑和粘滞性松弛作用的模拟结果相结合,与GPS观测值比较,图 2和3(绿色圆圈代表GPS观测值,不同颜色的曲线为不同粘滞系数的模拟值,橙色曲线η为9.5×1018 Pa ·s,蓝色曲线η为1.5×1019 Pa ·s,红色曲线η为2×1019 Pa ·s,青色曲线η为3×1019 Pa ·s)分别给出上述8个GPS观测站东向和北向震后位移变化的比较情况。可以看出,综合考虑震后余滑和粘滞性松弛作用模拟的震后地表形变与GPS观测值符合程度明显改善,这表明将这2种机制结合可以更为合理地解释MW9.0地震的震后形变。
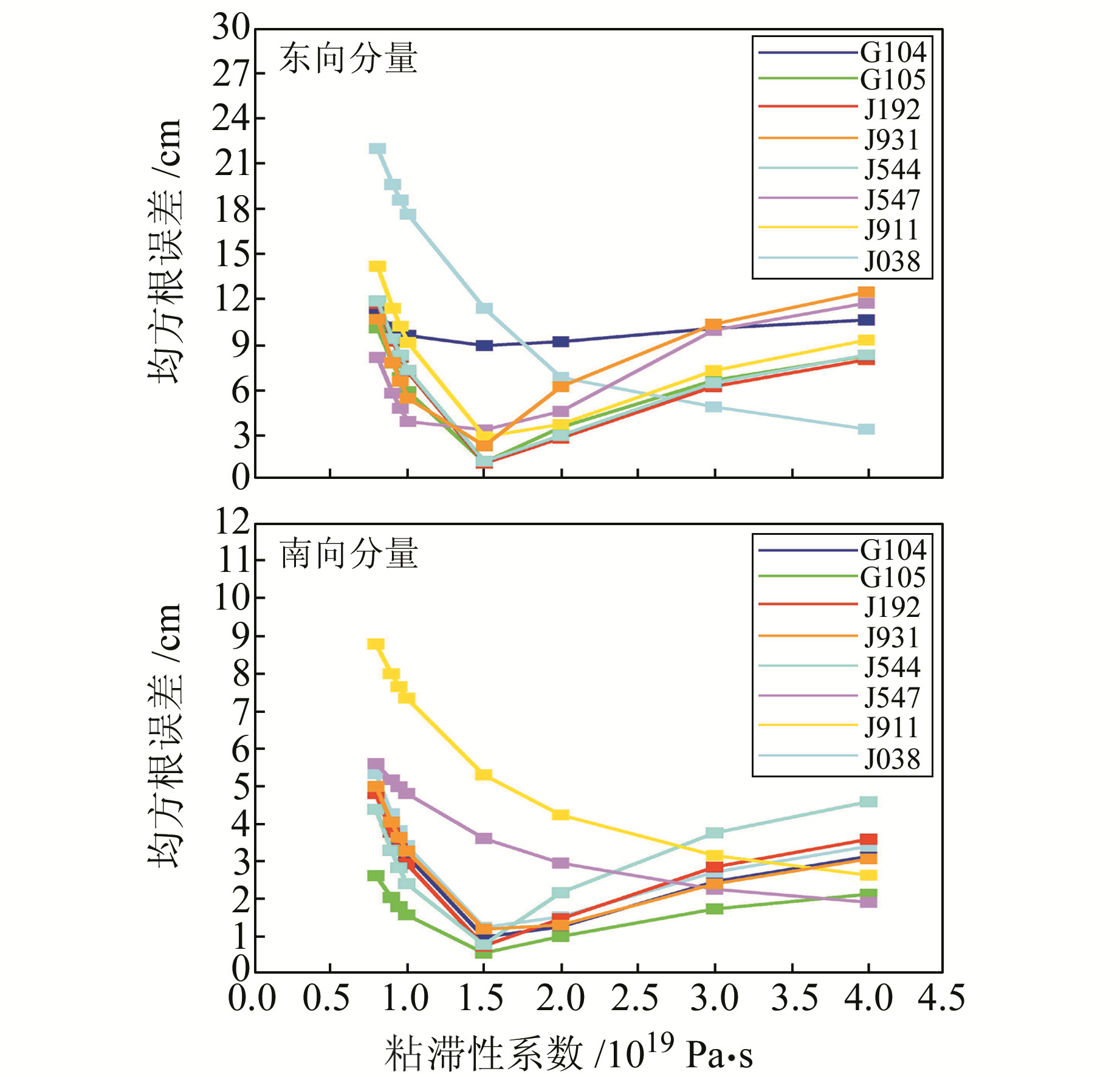
在模拟计算过程中,将粘滞系数进行调整时,模拟值与观测值的偏差会缩小或变大(图 2、3)。为估算该区域的最佳地幔粘滞系数,本文依据不同的地幔粘滞系数分别进行理论计算,然后计算其与GPS观测值之间的均方根误差(RMS),并获取均方根误差与粘滞系数的关系曲线,从而求取地幔粘滞系数的最优解。图 4给出了8个GPS观测点在不同粘滞系数下的模拟值与观测值之间的RMS数值。通过对8个GPS观测点的综合分析认为,当粘滞系数为1.5×1019 Pa ·s时,模拟值与观测值间的RMS误差最小,表明此时二者符合得最好,据此推断该区域的地幔粘滞系数在1.5×1019 Pa ·s量级。
|
图 4 不同地幔粘滞系数的对应的模拟值与GPS观测值之间的均方根误差 Fig. 4 The RMS errors between GPS observed and calculated with different mantle viscosities |
GPS观测显示,日本MW9.0地震在大区域范围内引起显著的震后变形,近5 a的震后位移累积达到东向60~165 cm,南向20~65 cm的量值,距震中较远处的G104、G105及J192站点所观测的震后位移累积变化已超过同震位移,且震后变形仍然持续,只是变化速率在逐渐减小。各GPS站震后位移随时间的变化规律均符合指数函数的衰减特性,可以利用修正的Omori公式拟合。日本岛较为密集的GPS观测网获得的显著同震和震后形变为认识大地震变形的动力学机理和区域介质性质提供了良好的观测依据。
单独利用震后余滑或粘滞性松弛作用机制都不能充分解释日本MW9.0地震的震后形变,联合利用这2种机制则能较合理地作出解释,表明大地震震后变形是受多种因素的物理机理共同作用和影响。日本MW9.0地震的震后余滑量非常大,尤其在震后的前1~2 a内,震后余滑对地表的变形起主要作用,控制整个区域的变形模式。震后余滑与同震断层滑动的模式较为接近,是由余震和断层蠕滑共同作用而成,在主要分布深度上与同震断层滑动比较接近,并向周边尤其深部扩展。这种作用产生的地表位移与同震位移方向一致,但变化速率随时间逐渐减小,使得其与GPS观测值的偏差逐渐增大,震后2 a后的地表变形逐渐转变为由粘滞松弛作用所控制。图 2和图 3显示,靠近震中区域的J547、J911和J038等3个站的震后形变模拟值与观测值的符合程度相对略差,这可能与靠近震中地区的变形机制更为复杂有关,如孔隙流体调整作用很有可能对震后的变形产生影响,需作进一步的研究。
基于粘滞性松弛作用对地表变形的影响,利用GPS观测的震后形变估算已成为推断区域地幔粘滞系数的重要方法[7, 18]。而以前,这一重要的地球动力学参数主要靠理论方法和经典的岩石实验估计[19]。本文粘弹性位错模拟结果显示,日本MW9.0地震区域的地幔粘滞系数在1.5×1019 Pa ·s量级。Hirth等[20]指出,根据实验室的资料计算,在海洋上地幔温压条件下,粘滞性系数应该在1×1019 Pa ·s量级,在俯冲带附近甚至会更低;Suito等[21]的模拟研究认为,日本俯冲带区域的粘滞系数为9.3×1018 Pa ·s;Wang[22]的统计表明,基于大地测量数据估算的俯冲带区域粘滞系数大多为(0.5~5)×1019 Pa ·s。因此本研究的结果与实验室岩石流变实验结果基本符合, 与其他研究者根据大地测量资料得到的结果也是吻合的。
| [1] |
Ozawa S, Nishimura T, Suito H, et al. Coseismic and Postseismic Slip of the 2011 Magnitude-9 Tohoku-Oki Earthquake[J]. Nature, 2011, 475(7 356): 373-376
(  0) 0) |
| [2] |
王敏, 李强, 王凡, 等. 全球定位系统测定的2011年日本宫城MW9.0地震远场同震位移[J]. 科学通报, 2011, 56(20): 1 593-1 596 (Wang Min, Li Qiang, Wang Fan, et al. Far-Field Coseismic Displacements Associated with the 2011 Tohoku-Oki Earthquake in Japan Observed by Global Positioning System[J]. Chinese Science Bulletin, 2011, 56(20): 1 593-1 596)
(  0) 0) |
| [3] |
Diao F, Xiong X, Wang R, et al. Overlapping Post-Seismic Deformation Processes: Afterslip and Viscoelastic Relaxation Following the 2011 MW9.0 Tohoku (Japan) Earthquake[J]. Geophysical Journal International, 2014, 196(1): 218-229 DOI:10.1093/gji/ggt376
(  0) 0) |
| [4] |
王丽凤, 刘杰, 赵金贵, 等. 2011年日本9.0级地震的同震位错以及震后应力松弛过程对中国大陆的影响[J]. 地震, 2013, 33(4): 238-247 (Wang Lifeng, Liu Jie, Zhao Jingui, et al. Coseismic Slip and Post-Seismic Relaxation of the 2011 MW9.0 Tohoku-Oki Earthquake and Its Influence on China Mainland[J]. Earthquake, 2013, 33(4): 238-247 DOI:10.3969/j.issn.1000-3274.2013.04.025)
(  0) 0) |
| [5] |
Shao Z, Zhan W, Zhang L, et al. Analysis of the Far-Field Co-Seismic and Post-Seismic Responses Caused by the 2011 MW9.0 Tohoku-Oki Earthquake[J]. Pure & Applied Geophysics, 2015, 173(2): 1-14
(  0) 0) |
| [6] |
Hsu Y J, Bechor N, Segall P, et al. Rapid Afterslip Following the 1999 Chi-Chi, Taiwan Earthquake[J]. Geophysical Research Letters, 2002, 29(16)
(  0) 0) |
| [7] |
Pollitz F F, Bürgmann R, Banerjee P. Post-Seismic Relaxation Following the Great 2004 Sumatra-Andaman Earthquake on a Compressible Self-Gravitating Earth[J]. Geophysical Journal International, 2006, 167(1): 397-420 DOI:10.1111/gji.2006.167.issue-1
(  0) 0) |
| [8] |
Jónsson S, Segall P, Pedersen R, et al. Post-Earthquake Ground Movements Correlated to Pore-Pressure Transients[J]. Nature, 2003, 424(6 945): 179-183
(  0) 0) |
| [9] |
朱守彪, 蔡永恩. 强震后地表变形的动力学机制研究——以1999年台湾集集地震为例[J]. 中国科学D辑:地球科学, 2009, 39(9): 1 209-1 219 (Zhu Shoubiao, Cai Yong'en. Dynamic Mechanisms of the Post-Seismic Deformation Following Large Events: Case Study of the 1999 Chi-Chi Earthquake in Taiwan of China[J]. Sci China Ser D:Earth Sci, 2009, 39(9): 1 209-1 219)
(  0) 0) |
| [10] |
Wang R, Lorenzo-Martín F, Roth F. PSGRN/PSCMP—A New Code for Calculating Co- and Post-Seismic Deformation, Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J]. Computers & Geosciences, 2006, 32(4): 527-541
(  0) 0) |
| [11] |
Shao G, Li X, Ji C, et al. Focal Mechanism and Slip History of the 2011 MW 9.1 off the Pacific Coast of Tohoku Earthquake, Constrained with Teleseismic Body and Surface Waves[J]. Earth Planets & Space, 2011, 63(7): 559-564
(  0) 0) |
| [12] |
Pollitz F F, Rol B, Paramesh B. Geodetic Slip Model of the 2011 MW9.0 Tohoku Earthquake[J]. Geophysical Research Letters, 2011, 38(7): 139-160
(  0) 0) |
| [13] |
Wei S, Graves R, Helmberger D, et al. Sources of Shaking and Flooding during the Tohoku-Oki Earthquake: A Mixture of Rupture Styles[J]. Earth & Planetary Science Letters, 2012, 333-334: 91-100
(  0) 0) |
| [14] |
Wang W, Sun W, Wu Y, et al. Modification of Fault Slip Models of the MW9.0 Tohoku Earthquake by Far Field GPS Observations[J]. Journal of Geodynamics, 2014, 75(4): 22-33
(  0) 0) |
| [15] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Physics of the Earth & Planetary Interiors, 1981, 25(4): 297-356
(  0) 0) |
| [16] |
Mooney W D, Laske G, Masters T G. CRUST 5.1: A Global Crustal Model at 5°×5°[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B1): 727-747 DOI:10.1029/97JB02122
(  0) 0) |
| [17] |
Zhou X, Sun W, Zhao B, et al. Geodetic Observations Detecting Coseismic Displacements and Gravity Changes Caused by the MW=9.0 Tohoku-Oki Earthquake[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B5): 81-88
(  0) 0) |
| [18] |
谭凯, 李杰, 王琪. 大地测量约束下的阿尔泰山岩石圈流变结构[J]. 地球物理学报, 2007, 50(6): 1 713-1 718 (Tan Kai, Li Jie, Wang Qi. Lithospheric Rheological Structure Constrained by Geodetic Data in Altay[J]. Chinese Journal of Geophysics, 2007, 50(6): 1 713-1 718)
(  0) 0) |
| [19] |
魏荣强, 臧绍先. 大陆岩石圈流变结构研究进展及存在问题[J]. 地球物理学进展, 2007, 22(2): 359-364 (Wei Rongqiang, Zang Shaoxian. Progresses and Problems in the Study of the Rheological Structure of the Continental Lithosphere[J]. Progress in Geophysics, 2007, 22(2): 359-364 DOI:10.3969/j.issn.1004-2903.2007.02.005)
(  0) 0) |
| [20] |
Hirth G, Kohlstedt D L. Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists[J]. AGU Monograph, 2003, 138: 83-105
(  0) 0) |
| [21] |
Suito H, Iizuka M, Hirahara K. 3-D Viscoelastic FEM Modeling of Crustal Deformation in Northeast Japan[J]. Pageoph, 2002, 159: 2 239-2 259 DOI:10.1007/s00024-002-8733-8
(  0) 0) |
| [22] |
Wang K. Elastic and Viscoelastic Models of Crustal Deformation in Subduction Earthquake Cycles[A]//Dixon T H, Moore J C. The Seismogenic Zone of Subduction Thrust Faults[M]. Columbia: Columbia University Press, 2007
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37