近年来,总体最小二乘[1]在测量数据处理领域得到了众多学者的关注和研究。总体最小二乘模型是非线性的[2],需要进行迭代计算[3-7]。尽管文献[3]~[7]的算法都能考虑数据不等精度和系数矩阵呈结构性的情况,但平差模型复杂且不能消除系数矩阵行列的相关性,而多元总体最小二乘[8-13]能较好地解决这一问题。多元总体最小二乘把观测向量和参数向量改写成矩阵形式,从而避免了系数矩阵大量重复元素和常数项的情况,简化了平差模型,同时也消除了系数矩阵行列的相关性[13]。文献[8]~[9]研究了多元总体最小二乘算法,并应用于坐标转换中,得到了较好的效果。文献[10]提出了多元加权总体最小二乘,但没有讨论系数矩阵含常数列的情况。文献[3]给出了一种拉格朗日方法的加权总体最小二乘算法,但并没有进行算例验证。文献[11]~[12]根据数值解法将多元总体最小二乘应用到坐标转换中。文献[13]提出了一种牛顿解法,解算效率较其他方法好,但存在算法迭代复杂、较依赖初值的问题。本文将多元加权总体最小二乘模型进行等价变换,将其转换为加权总体最小二乘模型,并给出了其计算流程。通过算例分析表明,本文算法简单易懂,便于操作。
1 多元总体最小二乘平差模型多元总体最小二乘模型为:
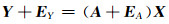
|
(1) |
式中,Y为m×n的观测矩阵,EY为m×n的观测值改正矩阵,A为m×r的系数矩阵,EA为m×r的系数改正矩阵,X为r×n的参数估值矩阵。
式(1)的随机模型为:
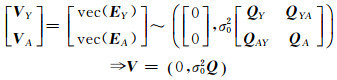
|
(2) |
总体最小二乘的估计准则为:
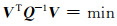
|
(3) |
将式(1)进行向量拉直运算:
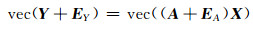
|
(4) |
根据拉直运算法则,化简得:
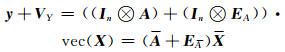
|
(5) |
进一步可以表示为:
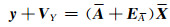
|
(6) |
式中,y为mn×1的观测向量,VY为mn×1的观测值改正向量,A为mn×rn的系数矩阵,EA为nm×nr的系数改正矩阵,X为rn×1的参数估值矩阵。
可以发现,通过变换后,式(1)表示成式(6),即将多元EIV模型转换成常规的EIV模型,其多元加权总体最小二乘的求解可以采用任意一种加权总体最小二乘算法。由于大部分加权总体最小二乘算法都需要构造系数矩阵的完整权阵,因此要求式(6)解的关键在于如何构造新的系数矩阵A的协因数阵QAA。由于系数矩阵A中存在大量的常数项或重复元素,而式(1)中的系数矩阵A中可能存在常数项和重复元素,会在VA中产生许多不需要改正的元素(改正数为0)。因此,可将系数矩阵的改正向量用结构矩阵来表示:
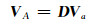
|
(7) |
式中,Va为t×1的系数矩阵中含误差的非重复元素的改正数(数量为t个),D为mr×t的结构矩阵。因此,式(5)的系数矩阵改正数可以表达为:
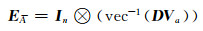
|
(8) |
式中,vec-1(·)为向量拉直运算的逆运算,即将向量重构成矩阵。根据式(7),可得到式(1)中系数矩阵元素的协因数阵:
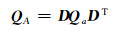
|
(9) |
将系数矩阵A的元素通过向量拉直运算得LA=vec(A),向量大小为mr×1,其对应的协因数阵为QA,大小为mr×mr。新的系数矩阵A是通过克罗内克积运算得到的,可将其表示成:
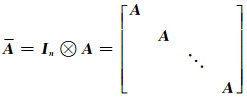
|
(10) |
式中,A包含n个A,其大小为mn×nr,令A = A1 … Ar,其中Ai的大小为m×1,则式(10)可以进一步表示为:
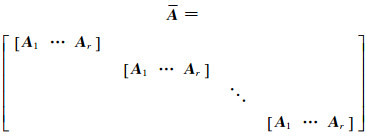
|
(11) |
将新的系数矩阵A拉直,并令LA=vec(A),其大小为mnnr×1,则可将其表示为LA的函数:
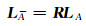
|
(12) |
式中, R为mnnr×mr的由0、1组成的常数矩阵,R =[R1T … R1T RrT]T,其中R1的个数为n-1,R1和Rr的构成为:
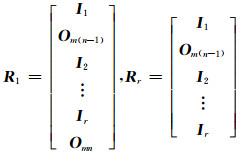
|
(13) |
式中,R1为(mnr+m)×mr的矩阵,Rr为(mnr-m(n-1))×mr的矩阵,因此由n-1个R1和1个Rr组成大小为mnnr×mr的R。其中I1、I2… Ir的组成为:

|
(14) |
式中,I1、I2… Ir的大小都为m×mr,式(13)中Om(n-1)为m(n-1)×mr的零矩阵,Omn为mn×mr的零矩阵。根据式(12),由协因数传播定律可得到新的系数矩阵元素的协因数阵:
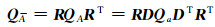
|
(15) |
通过上文分析,多元总体最小二乘模型(多元EIV模型)可以表示为常规的EIV模型,则多元加权总体最小二乘可以采用常规的加权总体最小二乘来解算。因此,可以将多元加权总体最小二乘模型和加权总体最小二乘模型统一表述为:
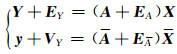
|
(16) |
式中,各矩阵的维数与式(5)相同,若n=1,则观测矩阵Y即为m×1的观测向量,待估参数即为r×1的向量,而式(10)的协因数构造,也就是QA= QA,就转化为普通的加权总体最小二乘模型。
2 多元加权总体最小二乘的迭代算法以Jazaeri加权总体最小二乘算法为例, 解算步骤如下。
1) 给出已知数据Y、A、D、QY、Qa。
2) 由已知数据构造新的系数矩阵A和系数矩阵元素的协因数阵QA,根据最小二乘原理计算参数的初值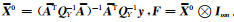
3) 根据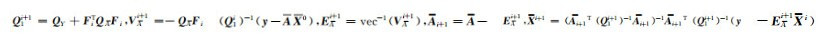
4) 重复步骤3),直到2次计算的参数之差小于给定的阈值ε,停止迭代并输出参数。
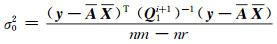
|
(17) |
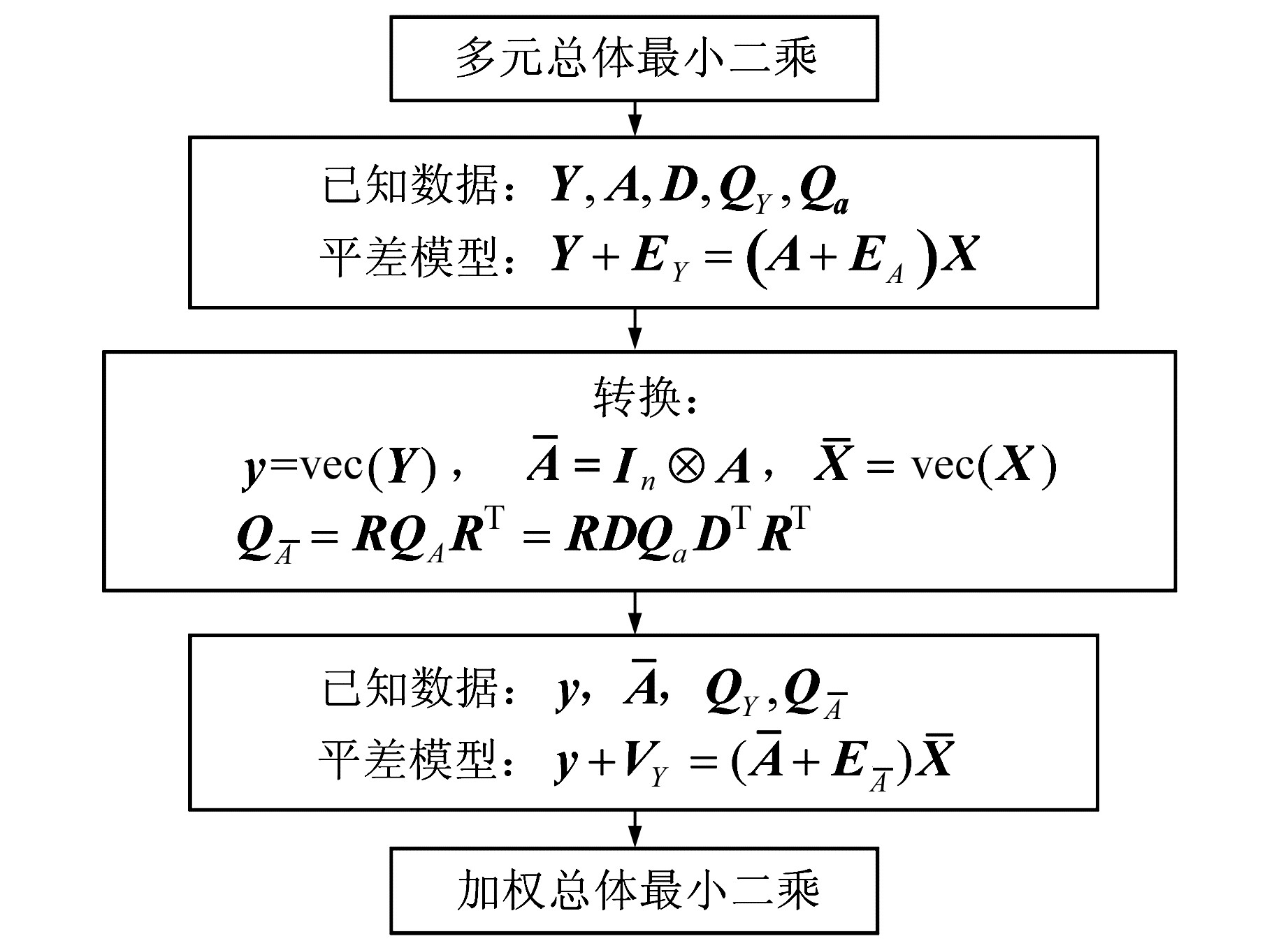
多元总体最小二乘转换为加权总体最小二乘解算的详细流程如图 1所示。
|
图 1 多元加权总体最小二乘解算流程 Fig. 1 The algorithm flow chart of mutltivariate weighted total least squares |
采用文献[5]中的实测数据(表 1),用具有两套坐标系的5个公共点来求取坐标转换参数,坐标观测值的权值为:
|
|
表 1 坐标观测值 Tab. 1 Coordinate observations of control points |

|

|
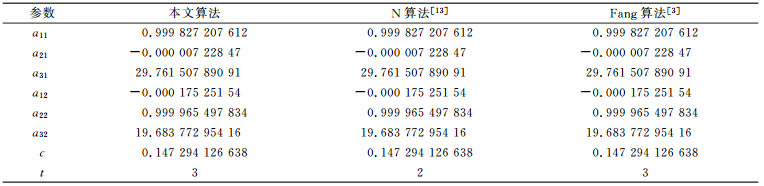
采用本文方法、文献[3]中的拉格朗日法(Fang算法)和文献[13]中的牛顿解法(N算法)等3种算法进行平差解算,迭代终止条件均为ε=10-12,参数的平均值、方差平均值c、迭代次数的平均值t如表 2所示。
|
|
表 2 平差结果 Tab. 2 Adjustment results |
从表 2的结果可以看出,本文方法解算的参数估值与拉格朗日法和牛顿解法解算的结果一致。从解算的迭代次数来看,本文算法和拉格朗日法都为3次,而牛顿解法为2次,说明本文算法与拉格朗日算法效率相当,而牛顿法的效率较高。这是因为牛顿法在解算时考虑了目标函数的二阶导数,但同时存在受初值影响大和公式推导过程复杂的问题。相比较而言,本文算法推导过程和解算都较为简单,且解算效率并未相差太大。
3.2 算例2为了进一步验证本文方法的有效性,采用文献[4]中的二维坐标转换模拟数据,转换参数的真值为a11=0.9、a12=-0.8、a21=1、a22=0.6、a31=0.7、a32=0.5,同时对源坐标和目标坐标施加相应的随机误差,误差的协因数阵为:
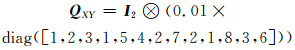
|
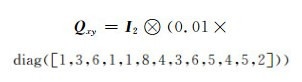
|
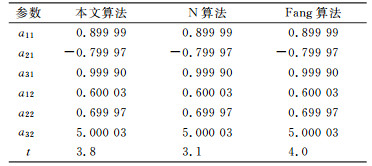
采用MATLAB软件的mvnrnd函数生成均值为0、方差协方差为0.001× QXY和0.001× Qxy的误差矩阵,将其分别施加到目标坐标和源坐标中。模拟1 000次试验,分别采用本文方法、Fang算法、N算法等3种算法进行平差解算,迭代终止条件均为ε=10-12,参数的平均值和迭代次数的平均值t见表 3。
|
|
表 3 平差结果 Tab. 3 Adjustment results |
从表 3的结果可以看出,对模拟数据进行1 000次试验后,3种方法得到的参数平均值结果一致,再次验证了本文算法的正确性。从迭代次数可以看出,本文算法的解算效率介于拉格朗日法和牛顿法之间,比拉格朗日法要好,稍差于牛顿法。
3.3 算例3采用文献[4]中的数据, 以给出的坐标转换真值和源坐标系坐标值计算得到目标坐标系的坐标,坐标真值为a11=0.9、a12=-0.8、a21=1、a22=0.6、a31=0.7、a32=0.5。使用MATLAB软件生成协因数阵Qr=randn(100, 26)T×randn(100, 26), 利用函数mvnrnd生成均值为0、方差协方差为0.001× Qr的误差矩阵,将误差矩阵施加到坐标观测值中。采用本文方法模拟10 000次,迭代终止条件均为10-12,由10 000次平差计算得到的参数估值的直方图如图 2所示。

|
图 2 参数估值的直方图 Fig. 2 Histograms of estimated parameters |
可以看出,10 000次随机试验的参数直方图分布近似正态分布,图中出现频数最多的参数值与真值几乎一致,且图形以真值为对称轴,这进一步说明了本文算法的有效性和可行性。
4 结语1) 将多元加权总体最小二乘模型进行变换,转换成加权总体最小二乘模型,并根据Jazaeri加权总体最小二乘算法提出了一种相应的解算方法。
2) 提出的多元加权总体最小二乘新解法,推导过程简捷,迭代算法与加权总体最小二乘法类似。
3) 通过3个算例验证了本文算法的正确性,在解算效率上介于拉格朗日法和牛顿法之间,尽管不及牛顿法,但就算法的公式推导和编程运算,本文方法更为简单。
| [1] |
Golub G H, Loan C F. An Analysis of the Total Least Squares Problem[J]. SIAM J Numer Anal, 1980, 17: 883-893 DOI:10.1137/0717073
(  0) 0) |
| [2] |
汪奇生. 线性回归模型的总体最小二乘平差算法及其应用研究[D]. 昆明: 昆明理工大学, 2014 (Wang Qisheng. Research on the Total Least Squares Adjustment Algorithm for Linear Regression Model and Its Application[D]. Kunming: Kunming University of Science and Technology, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10674-1015547948.htm
(  0) 0) |
| [3] |
Fang X. Weighted Total Least Squares Solutions for Applications in Geodesy[D]. Hanover: Leibniz University of Hanover, 2011
(  0) 0) |
| [4] |
Mahboub V. On Weighted Total Least-Squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5): 359-367 DOI:10.1007/s00190-011-0524-5
(  0) 0) |
| [5] |
Jazaeri S, Amiri-Simkooei A R, Sharifi M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19-27 DOI:10.1179/1752270613Y.0000000052
(  0) 0) |
| [6] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-In-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [7] |
汪奇生, 杨德宏, 杨腾飞. EIV模型参数估计的新方法[J]. 武汉大学学报:信息科学版, 2016, 41(3): 356-360 (Wang Qisheng, Yang Dehong, Yang Tengfei. A New Method of Parameter Estimation for the EIV Model[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 356-360)
(  0) 0) |
| [8] |
Schaffrin B, Felus Y A. Multivariate Total Least–Squares Adjustment for Empirical Affine Transformations[C]. Ⅵ Hotine-Marussi Symposium on Theoretical and Computational Geodesy: Challenge and Role of Modern Geodesy, Wuhan, 2008 https://link.springer.com/chapter/10.1007%2F978-3-540-74584-6_38
(  0) 0) |
| [9] |
Schaffrin B, Felus Y A. On the Multivariate Total Least-Squares Approach to Empirical Coordinate Transformations.Three Algorithms[J]. Journal of Geodesy, 2008, 82(6): 373-383 DOI:10.1007/s00190-007-0186-5
(  0) 0) |
| [10] |
Schaffrin B, Wieser A. Empirical Affine Reference Frame Transformations by Weighted Multivariate TLS Adjustment[J]. Geodetic Reference Frames, 2009, 13(4): 213-218
(  0) 0) |
| [11] |
孙大双, 张友阳, 黄令勇, 等. 多元总体最小二乘在大旋转角三维坐标转换中的应用[J]. 测绘科学技术学报, 2014, 31(5): 481-485 (Sun Dashuang, Zhang Youyang, Huang Lingyong, et al. Application of Multivariate Total Least Squares Method in Three-Dimension Coordinate Conversion with Large Rotation Angle[J]. Journal of Geomatics Science and Technology, 2014, 31(5): 481-485 DOI:10.3969/j.issn.1673-6338.2014.05.009)
(  0) 0) |
| [12] |
黄令勇, 吕志平, 任雅奇, 等. 多元总体最小二乘在三维坐标转换中的应用[J]. 武汉大学学报:信息科学版, 2014, 39(7): 793-798 (Huang Lingyong, Lü Zhiping, Ren Yaqi, et al. Application of Multivariate Total Least Square in Three-Dimensional Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 793-798)
(  0) 0) |
| [13] |
王乐洋, 赵英文, 陈晓勇, 等. 多元总体最小二乘问题的牛顿解法[J]. 测绘学报, 2016, 45(4): 411-417 (Wang Leyang, Zhao Yingwen, Chen Xiaoyong, et al. A Newton Algorithm for Multivariate Total Least Squares Problems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 411-417)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37