2. 河南省地质矿产勘查开发局,郑州市金水路28号,450012
三维空间直角坐标转换中,布尔莎(Bursa)模型、莫洛金斯基(Molodensky)模型和武测模型等被广泛应用。常用的三维坐标转换模型采用最小二乘原理[1],将七参数模型误差方程线性化后,建立高斯-马尔可夫迭代模型求解坐标转换七参数,在小角度坐标转换情况下,误差可以忽略,因此这些坐标转换模型及其参数的求解方法适用于小角度的坐标旋转变换[2-4]。为解决大角度的坐标旋转问题,国内外学者提出了多种三维空间直角坐标转换方法,其中最具代表性的包括方向余弦法[5]、罗德里格矩阵法[6]以及旋转矩阵的SVD估计法[7]等,均取得了较好的效果。然而,上述方法与传统的欧拉角迭代方法一样,是基于坐标转换七参数模型的迭代解法[8],在解算过程中,计算繁琐且计算周期长。本文针对三维空间坐标转换模型的七参数求解问题,通过坐标重心化[9]求解坐标转换的尺度参数,引入对偶四元数[10]来构造坐标转换旋转矩阵和平移向量,推导基于对偶四元数的三维空间坐标转换模型的直接解法。最后,通过算例以小角度、中角度以及大角度等不同情况验证该算法的正确性和适用性。
1 对偶四元数及其旋转平移 1.1 对偶四元数对偶四元数的数学形式为[11]:
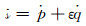
|
(1) |
式中,ṗ为对偶四元数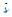
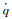
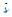
四元数是一个超复数,假设任意一个四元数记为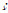
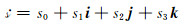
|
(2) |
式中,i、j、k为四元数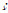
利用对偶四元数描述坐标系间的旋转和平移变换,如图 1所示。为了简单和方便描述,这里把旋转轴和平移轴重合处理,假设向量l为旋转轴,角θ为旋转角,水平距离d表示沿着向量l方向平移的距离。坐标系间的旋转和平移变换(刚体的螺旋运动)可以用一个对偶四元数进行描述。假设该对偶四元数为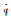
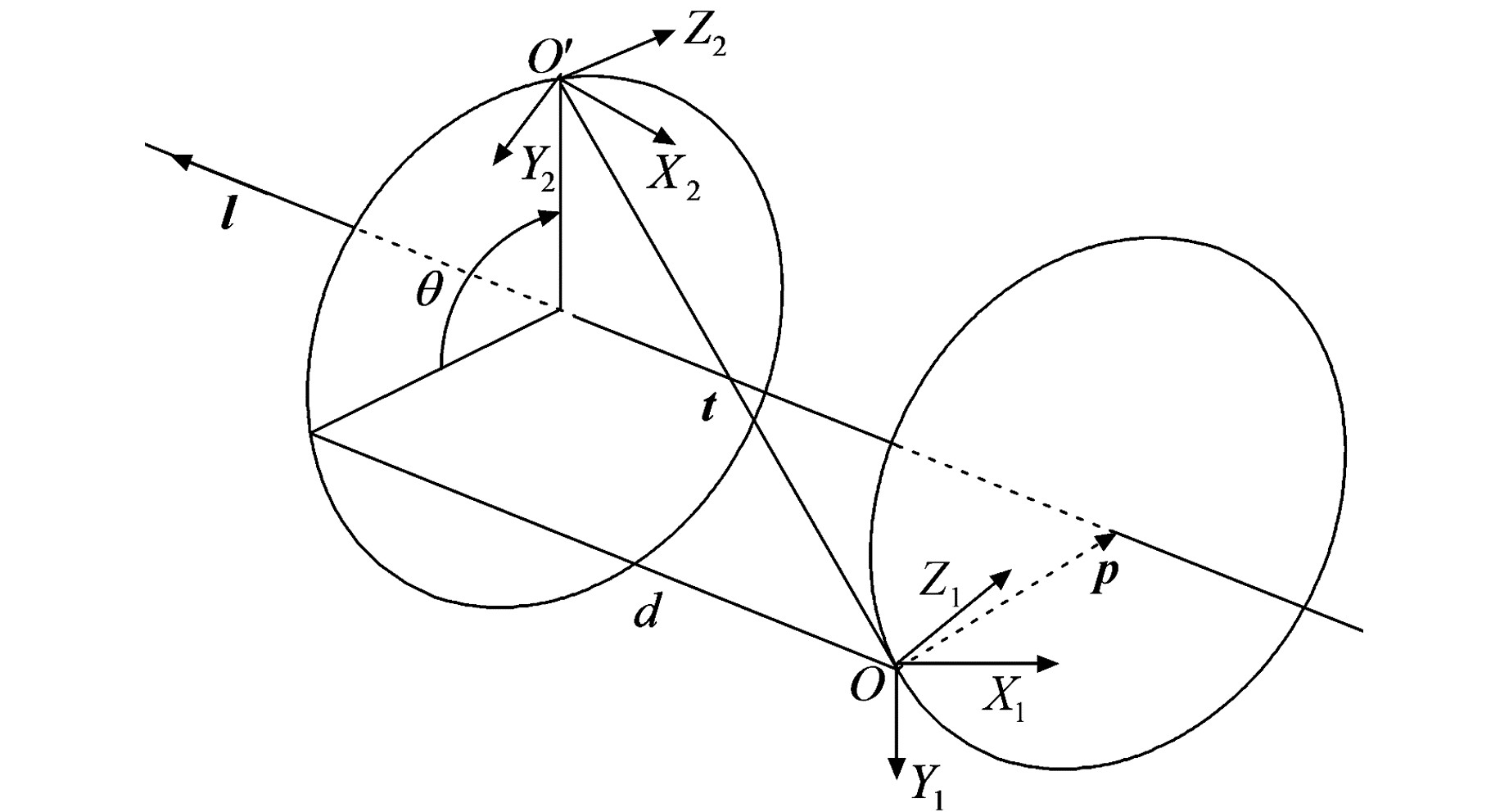
|
图 1 旋转和平移变换的对偶四元数描述 Fig. 1 Description of rotation and translation transformation of dual quaternion |
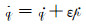
|
(3) |
式中,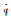

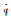
按照四元数格拉斯曼乘积以及四元数的矩阵形式[11],描述旋转的旋转矩阵R和描述平移的向量T可以同时用对偶四元数的实部和对偶部进行表示,其形式为:
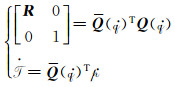
|
(4) |
式中,
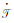
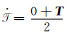
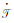
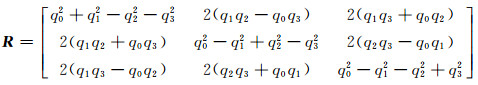
|
(5) |
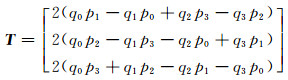
|
(6) |
假设三维空间两个坐标系分别为O-X1Y1Z1和O′-X2Y2Z2,空间一点A在坐标系O-X1Y1Z1的坐标[X1 Y1 Z1]T通过绕Z1轴旋转α角、绕X1轴旋转β角以及绕Y1旋转γ角作3次旋转,最终得到空间坐标系O′-X2Y2Z2的坐标[X2 Y2 Z2]T。其相应的坐标转换公式可表示为:
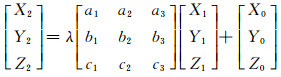
|
(7) |
式中,a1、a2、a3分别表示X1轴与X2、Y2、Z2轴的方向余弦,b1、b2、b3分别表示Y1轴与X2、Y2、Z2轴的方向余弦,c1、c2、c3分别表示Z1轴与X2、Y2、Z2轴的方向余弦,λ为坐标转换的尺度参数,[X0 Y0 Z0]T表示坐标转换的平移向量。将式(7)写成矢量的形式为:
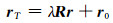
|
(8) |
式中,向量rT表示坐标系O′-X2Y2Z2的坐标向量,向量r表示坐标系O-X1Y1Z1的坐标向量,矩阵R为两个坐标系之间的旋转矩阵,向量r0为两个坐标系之间的平移向量。
2.2 坐标转换参数的求解假设两个不同的坐标系O-X1Y1Z1和O′-X2Y2Z2拥有n个控制点相对应的两套坐标系坐标,分别为[X1i Y1i Z1i]T和[X2i Y2i Z2i]T(i=1, …, n),利用相对应的两套不同坐标系坐标求解两个坐标系间的坐标转换参数。求取两个坐标系间的尺度参数可参考文献[9]。首先分别将两个坐标系的n个控制点坐标重心化。其中,坐标系O-X1Y1Z1的重心化坐标表示为[X1i, Y1i, Z1i](i=1, …, n),坐标系O′-X2Y2Z2的重心化坐标表示为[X2i, Y2i, Z2i](i=1, …, n)。建立误差方程之后,利用最小二乘原理计算求取坐标系间转换的尺度参数λ,即
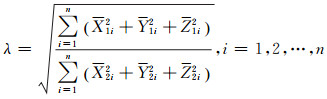
|
(9) |
求解出尺度参数之后,再求解姿态参数描述的旋转矩阵R。由式(8)可得,坐标转换的误差方程形式为:
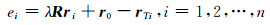
|
(10) |
将误差方程式(10)中n个控制点的平均误差最小,令最小误差函数为:

|
(11) |
假设这里用于描述旋转和平移的对偶四元数为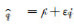
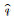
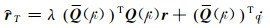
|
(12) |
将式(12)中对偶四元数描述的坐标转换方程代入式(11),整理得:
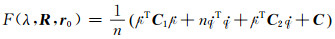
|
(13) |
式中,
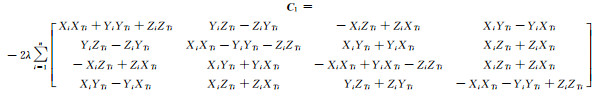
|
(14) |
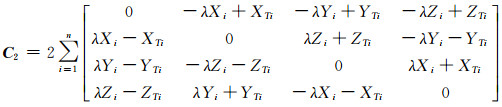
|
(15) |
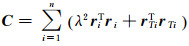
|
(16) |
采用拉格朗日法对式(13)求极值,然后对四元数ṗ和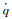
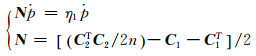
|
(17) |
式中,η1为矩阵N的特征值。要让函数F(λ, R, r0)最小,则只需使特征值η1最大,即求取矩阵N的最大特征值,矩阵N的最大特征值对应的特征向量即为四元数ṗ的矩阵形式,将其代入式(5)中即可求出旋转矩阵R;将四元数ṗ代入式(17),即可求解出四元数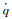
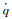
为验证基于对偶四元数的三维空间坐标转换算法的正确性和适用性,设计了坐标转换小角度、中角度以及大角度等3种情况进行模拟实验。假设坐标系O-X1Y1Z1为源坐标系,坐标系O′-X2Y2Z2为目标坐标系,源坐标系中有12个控制点,相对应的目标坐标系中同时也有12个目标坐标系坐标,源坐标系按照绕旋转轴Z轴、X轴和Y轴的顺序依次逆时针旋转,相应的旋转角即为α、β、γ;然后按照[X0 Y0 Z0]T进行平移变换,同时两个坐标系之间存在一个尺度参数λ。源坐标系12个控制点坐标如表 1所示,不同角度模型的参数如表 2所示。结合表 1和2,通过式(7)计算得到的目标坐标系坐标如表 3所示。
|
|
表 1 源坐标系控制点坐标 Tab. 1 Control-points coordinates of original coordinates system |
|
|
表 2 不同角度模型的坐标转换参数 Tab. 2 Coordinate conversion parameters of the different angle model |
|
|
表 3 目标坐标系控制点坐标 Tab. 3 Control-points coordinates of target coordinate system |
以MATLAB为仿真平台,采用文中所提对偶四元数的坐标转换参数直接解法(算法1)和传统欧拉角迭代解法[12](算法2),分别对源坐标系控制点坐标和对应的目标坐标系控制点坐标进行坐标系间转换参数的求解,并从计算结果和计算时间两个方面进行比较(表 4)。
|
|
表 4 解算结果比较 Tab. 4 Comparison of solution results |
表 4的解算结果比较验证了文中所提基于对偶四元数的三维空间坐标转换直接解法是正确的,算法1的解算结果要优于算法2,且克服了算法2不适用于大旋转角度的劣势。在解算时间上,算法1的计算时间远小于算法2,如果用于区域网平差,效果会更加明显。基于对偶四元数的三维空间坐标转换直接解法无需计算初始值,可以直接计算,且无需线性化和迭代计算,对于大旋转角度的坐标系间的旋转依然能求解出较高精度的坐标转换参数。
4 结语本文从对偶四元数的定义及其性质入手,描述了对偶四元数在表达坐标系间旋转和平移方面的便利表达形式。针对三维空间坐标转换模型的七参数求解问题,通过坐标重心化求解坐标转换的尺度参数,同时考虑到对偶四元数在描述旋转矩阵和平移向量中的优势,可以有效地克服旋转和平移的耦合误差,引入对偶四元数来构造坐标转换旋转矩阵和平移向量,推导了一种基于对偶四元数的三维空间坐标转换模型的直接解法。该算法与传统的欧拉角迭代算法相比,有效地克服了繁琐的三角运算,无需对旋转参数线性化、无需迭代而直接求解坐标转换的七参数,模型更加简单,计算简便。最后通过仿真实验表明,基于对偶四元数的三维空间坐标转换直接解法具有无需迭代、计算速度快、解算精度高等特点,且适用于大旋转角度的三维空间坐标系间的转换。
| [1] |
刘毅, 岳建平, 卢银宏, 等. 补偿最小二乘法在大地坐标转换中的应用[J]. 测绘工程, 2012, 21(5): 80-82 (Liu Yi, Yue Jianping, Lu Yinhong, et al. Application of Penalized Least Squares Method in Geodetic Coordinate System Transformation[J]. Engineering of Surveying and Mapping, 2012, 21(5): 80-82 DOI:10.3969/j.issn.1006-7949.2012.05.021)
(  0) 0) |
| [2] |
潘国荣, 汪大超, 周跃寅. 两种大转角空间坐标转换模型研究[J]. 山东科技大学学报:自然科学版, 2015, 34(1): 61-67 (Pan Guorong, Wang Dachao, Zhou Yueyin. Two Spatial Coordinate Transformation Model of Large Angle[J]. Journal of Shandong University of Science and Technology: Natural Science, 2015, 34(1): 61-67)
(  0) 0) |
| [3] |
王传江, 王解先, 顾建祥. 大旋转角三维直角坐标转换的一种线性模型[J]. 铁道勘察, 2013, 38(6): 4-6 (Wang Chuanjiang, Wang Jiexian, Gu Jianxiang. A Linear Model of 3-Dimensional Rectangular Coordinate Transformation Based on Big Rotation Angle[J]. Railway Investigation and Surveying, 2013, 38(6): 4-6 DOI:10.3969/j.issn.1672-7479.2013.06.002)
(  0) 0) |
| [4] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报:信息科学版, 2012, 37(3): 253-256 (Yao Yibin, Huang Chengmeng, Li Chengchun, et al. A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle's 3D Coordinate[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3): 253-256)
(  0) 0) |
| [5] |
陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1 101-1 105 (Chen Yi, Shen Yunzhong, Liu Dajie. A Simplified Model of Three Dimensional-Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1 101-1 105)
(  0) 0) |
| [6] |
原玉磊, 蒋理兴, 刘灵杰. 罗德里格矩阵在坐标系转换中的应用[J]. 测绘科学, 2010, 35(2): 178-179 (Yuan Yulei, Jiang Lixing, Liu Lingjie. Applications of Lodrigues Matrix in Coordinates Transformation[J]. Science of Surveying and Mapping, 2010, 35(2): 178-179)
(  0) 0) |
| [7] |
刘志平, 杨磊. 大旋转角的空间直角坐标转换方法的改进[J]. 大地测量与地球动力学, 2016, 36(7): 586-590 (Liu Zhiping, Yang Lei. An Improved Method for Spatial Rectangular Coordinate Transformation with Big Rotation Angle[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 586-590)
(  0) 0) |
| [8] |
谭骏祥, 李少达, 杨容浩. 基于非迭代与迭代法联合估计的七参数坐标转换方法研究[J]. 大地测量与地球动力学, 2014, 34(1): 131-134 (Tan Junxiang, Li Shaoda, Yang Ronghao. Study on Seven-Parameter Coordinate Transformation Model Based on Combined Estimation of Non-Iteration and Iteration[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 131-134)
(  0) 0) |
| [9] |
杜兰, 张捍卫, 周庆勇, 等. 坐标转换参数之间的相关性解析[J]. 大地测量与地球动力学, 2011, 31(1): 59-62 (Du Lan, Zhang Hanwei, Zhou Qingyong, et al. Analysis of Correlation of Coordinate Transformation Parameters[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 59-62)
(  0) 0) |
| [10] |
Pujol J. On Hamilton's Nearly-Forgotten Early Work on the Relation between Rotations and Quaternions and on the Composition of Rotation[J]. American Mathematical Monthly, 2014, 121(6): 515-522 DOI:10.4169/amer.math.monthly.121.06.515
(  0) 0) |
| [11] |
张捍卫, 李明艳, 李克昭. 四元数理论及其在坐标转换中的应用[J]. 大地测量与地球动力学, 2015, 35(5): 807-810 (Zhang Hanwei, Li Mingyan, Li Kezhao. The Quaternion Theory and Its Application in Coordinate Transformation[J]. Journal of Geodesy and Geodynamics, 2015, 35(5): 807-810)
(  0) 0) |
| [12] |
吕志鹏, 伍吉仓. 三维坐标变换算法的比较[J]. 大地测量与地球动力学, 2016, 36(1): 35-39 (Lü Zhipeng, Wu Jicang. Comparison of Three-Dimensional Coordinate Transformation Algorithms[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 35-39)
(  0) 0) |
2. Henan Bureau of Geo-Exploration and Mineral Development, 28 Jinshui Road, Zhengzhou 450012, China
 2017, Vol. 37
2017, Vol. 37






