GPS动态定位技术由于其定位精度高、全天候、可靠性强以及成本低等因素常用于建筑物形变监测[1-2]。一般情况下,传统的RTK双差模式可以很好地消除参考站和监测站之间的电离层和对流层延迟误差,而随着建筑物楼层不断增加,楼底和楼顶之间的空气湿度分布状况差异也越来越大,利用参考站和监测站站间作差并不能很好地消除GPS数据中的对流层湿延迟误差,其残余对流层误差必定会影响传统RTK的定位精度,因此理论上超高层建筑GPS动态监测中必须考虑其残余误差的影响。
对流层延迟误差分为干延迟和湿延迟,干延迟较为稳定,可以通过模型进行改正[3-4];而湿延迟变化主要与空气湿度相关,无法较好地通过模型进行改正。文献[5]通过GAMIT软件将对流层湿延迟进行分段估计,需要较长的观测时间,不能用于实时动态RTK模式监测;网络RTK虽然能够实时获取监测站的对流层延迟信息,但至少需要3个同步观测基站,对于无基站覆盖的区域无法实现定位。针对单基站超高层GPS实时动态监测系统,本文在传统RTK技术的基础上,对残余对流层误差利用卡尔曼滤波进行参数估计[6-7]。考虑到对流层随时间变化的规律[8],历元之间对流层天顶延迟采用随机游走过程进行相互约束,并给出相应的数据处理方法。实验部分通过高差约280 m的超高层建筑GPS监测数据,验证参考站和监测站之间对流层残余误差不可忽略,在对其进行参数估计后动态RTK定位精度得到提高,尤其是在高程方向上。
1 方法 1.1 双差模型GPS卫星观测值包括伪距和载波相位观测值,在卫星-接收机i-r上分别用Pri和φri表示。观测方程可以表示为:
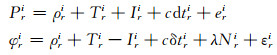
|
(1) |
式中,ρrs表示卫星-接收机i-r几何距离,Tri和Iri分别表示对流层和电离层延迟量,dtri和δtri分别表示伪距和载波对应的卫星-接收机钟差,c表示光速,eri和εri分别表示伪距和载波观测值噪声,Nri表示载波相位观测值整周模糊度,λ表示对应的波长。
由于式(1)中包含卫星-接收机钟差项,可以采用2个接收机(r, b)和2颗卫星(i, j)构成经典的双差观测方程:
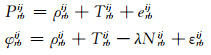
|
(2) |
式中,ρrbij=ρri-ρrj-(ρbi-ρbj),Nrbij表示双差模糊度参数。
双差对流层延迟Trbij可以分解为参考站和流动站天顶方向延迟:
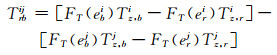
|
(3) |
式中,Tz, b、Tz, r分别表示参考站和流动站天顶方向的对流层湿延迟量;FT为对流层投影函数,采用GMF模型[8],与高度角相关。
引入平均高度角ϑ:
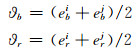
|
(4) |
结合式(3)和(4),得到简化后的双差对流层延迟误差模型:
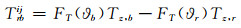
|
(5) |
利用卡尔曼滤波对坐标参数、双差对流层误差以及模糊度参数进行状态估计,动态卡尔曼滤波模型为:
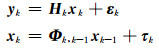
|
(6) |
式中,yk表示GPS观测值向量,即(φ*, P*)T;xk表示待估参数状态向量,即(X, Y, Z, Tz, b, Tz, r, Nbr12, ...Nbr1m)T,其中X、Y、Z表示接收机三维坐标;卫星1表示参考星,共观测m颗卫星;Hk表示状态向量对应的设计矩阵;Φk, k-1表示观测历元之间的状态转移矩阵,为单位矩阵。
在利用卡尔曼滤波进行参数估计时,初值的给定非常重要。根据经验,初始历元给定参考站和流动站天顶方向对流层湿延迟量均为0.15 m,对应的方差给定为0.3 m2。
对流层湿延迟随时间的变化虽然无明显规律,但其比较符合随机游走的过程[10-11],即具有明显的空间和时间相关性。为了提高卡尔曼滤波精度,在对对流层参数进行滤波时,历元之间给定一个过程噪声δT2。考虑到超高层建筑参考站和监测站空间距离较短,δT2只与时间分布相关:

|
(7) |
式中,δ0为对流层基本过程噪声,取为0.001 m;T为连续历元时间间隔。
2 实验与分析GPS动态监测数据采集于国内某在建超高层建筑(高度约300 m),其中参考站架设在高度约20 m的稳定居民楼楼顶,监测站架设在正在建造中的超高层楼楼顶,与参考站高差约280 m,平面距离约320 m。利用Trimble-NetR9接收机同步观测约10 h,采样间隔5 s,截止高度角设置为15°,天气状况为晴天、无风。
采用自主研制的GPS实时动态定位软件对实验数据进行事后RTK模式处理。其中对流层延迟误差采用2种方法进行处理:方法1,Saastamoinen模型改正;方法2,Saastamoinen模型改正+参数估计法改正。
实际上方法1中的模型改正主要是对对流层干延迟进行改正,传统RTK常采用该法,而方法2中的干延迟改正加上湿延迟参数估计是下文介绍的方法。
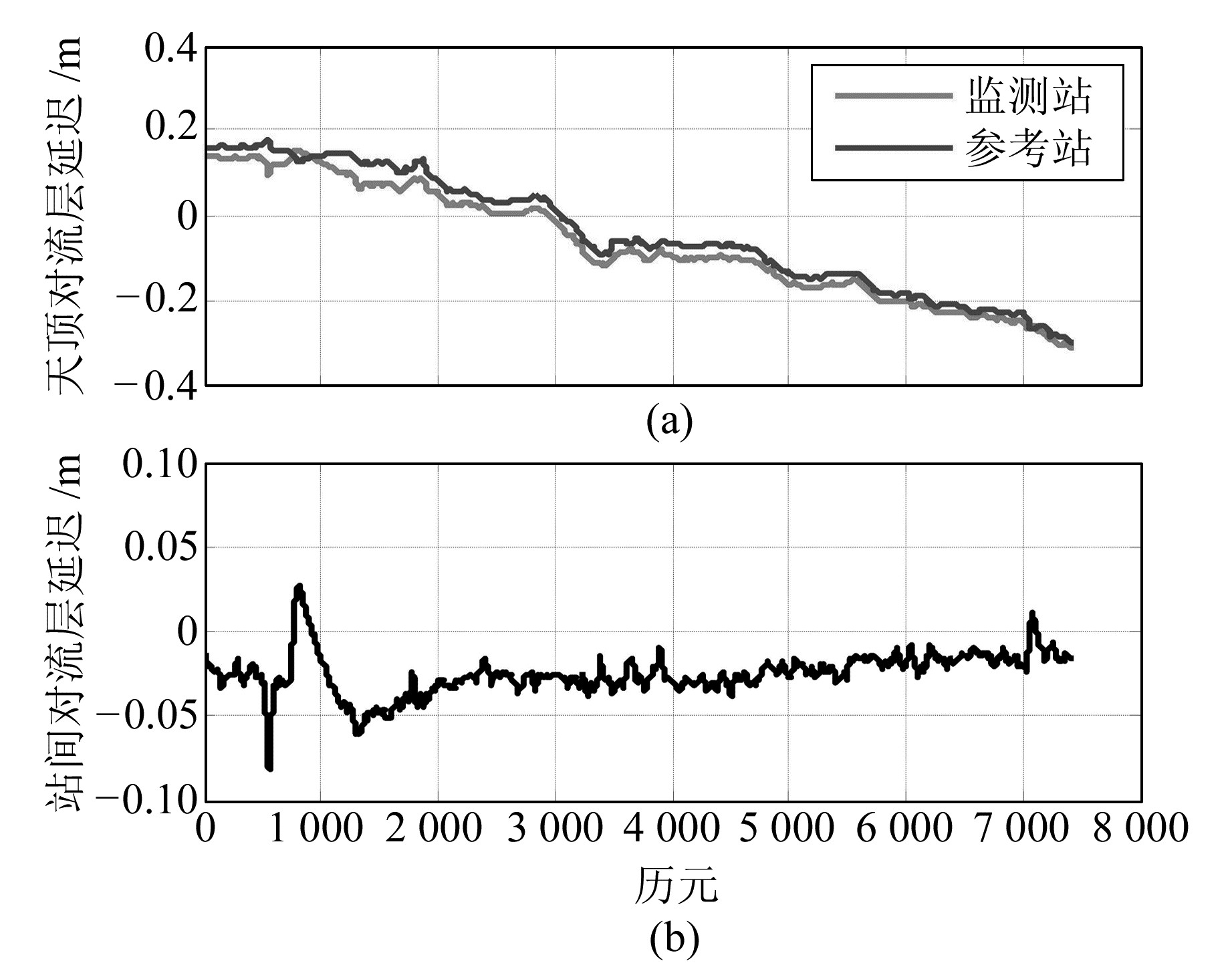
图 1(a)给出了监测站和参考站天顶方向对流层湿延迟估计量随历元变化的趋势。可以看出,天顶方向湿延迟误差最高可达0.35 m,随时间变化相对比较平稳,没有出现大的波动,比较符合GPS对流层湿延迟随机游走的过程。将参考站和监测站天顶方向延迟量作差,其变化趋势如图 1(b)所示。可以看出,站间单差天顶方向残余对流层误差平均在2 cm左右,最高可达5 cm。可以预测,随着该超高层建筑物的继续施工,楼层越来越高,在利用GPS监测时站间对流层天顶延迟差异也会越来越明显。
|
图 1 监测站和参考站天顶方向对流层湿延迟量 Fig. 1 The zenith wet tropospheric delay of monitoring station and reference station |
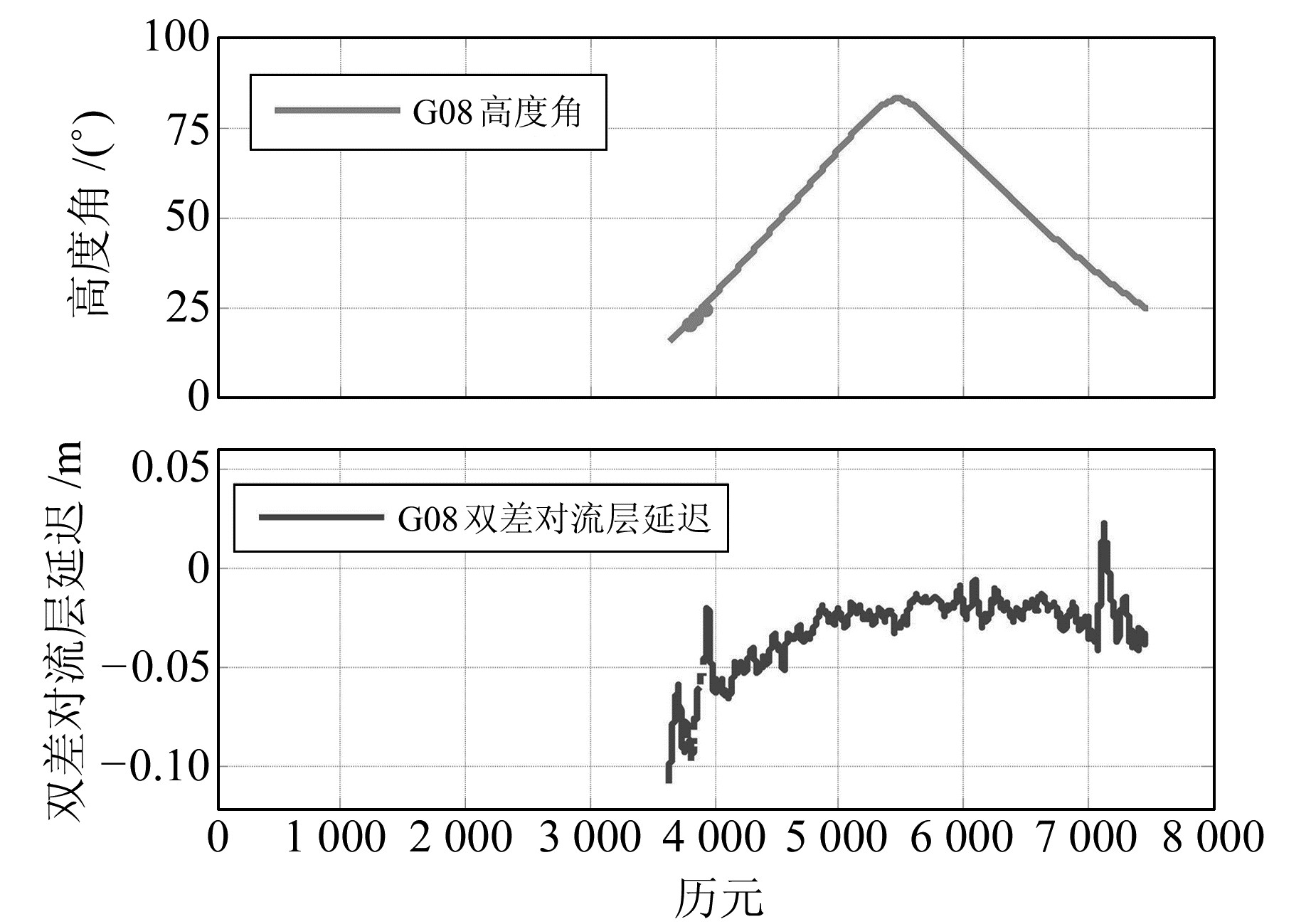
考虑到对流层延迟与卫星高度角相关,在估计出天顶方向对流层延迟量后,可根据投影函数得到相应的对流层斜延迟误差。选取观测时段相对较长的2颗卫星,分别是G08和G26号卫星,图 2和3反映了它们在观测时段内的高度角以及站间双差对流层斜延迟误差,由于基准站和流动站对应的卫星高度角非常接近,图中给出的实际上是平均高度角。可以看出,G08号卫星双差对流层延迟误差最高可达11 cm,G26号卫星最高可达10 cm,即在高差约280 m的超高层建筑上进行GPS同步观测,双差对流层残余误差可达到1 dm,相当于GPS约半个波长(L1)的误差,显然不能简单地忽略。另外,对比高度角的变化趋势可以发现,对流层斜延迟量与高度角密切相关,一般情况下高度角越低,斜延迟量也越大。因此在进行超高层建筑GPS动态监测时,可以适当地增大截止高度角,能够有效地减弱对流层延迟误差的影响。
|
图 2 G08卫星高度角以及站间双差对流层残余延迟 Fig. 2 G08 satellite elevation and the residual delay of the double difference troposphere |

|
图 3 G26卫星高度角以及站间双差对流层残余延迟 Fig. 3 G26 satellite elevation and the residual delay of the double difference troposphere |
为了进一步验证对流层参数估计改正对最终GPS动态定位结果的影响,统计方法1和方法2对应的RTK定位精度。根据激光垂准仪监测数据显示,本次GPS观测时段内楼层没有出现摆动,可认为是静止状态。利用高精度GPS静态处理软件GAMIT得到监测站的精确坐标,与方法1和方法2对应的RTK定位结果作对比,图 4给出了3个方向(E、N、U)的单历元定位精度。可以看出,2种方法对应的东方向和北方向定位精度基本一致,但U方向方法1相对于真值出现了约8 cm的系统偏差,经过对流程残余误差参数估计并改正后,U方向定位精度大为提高。
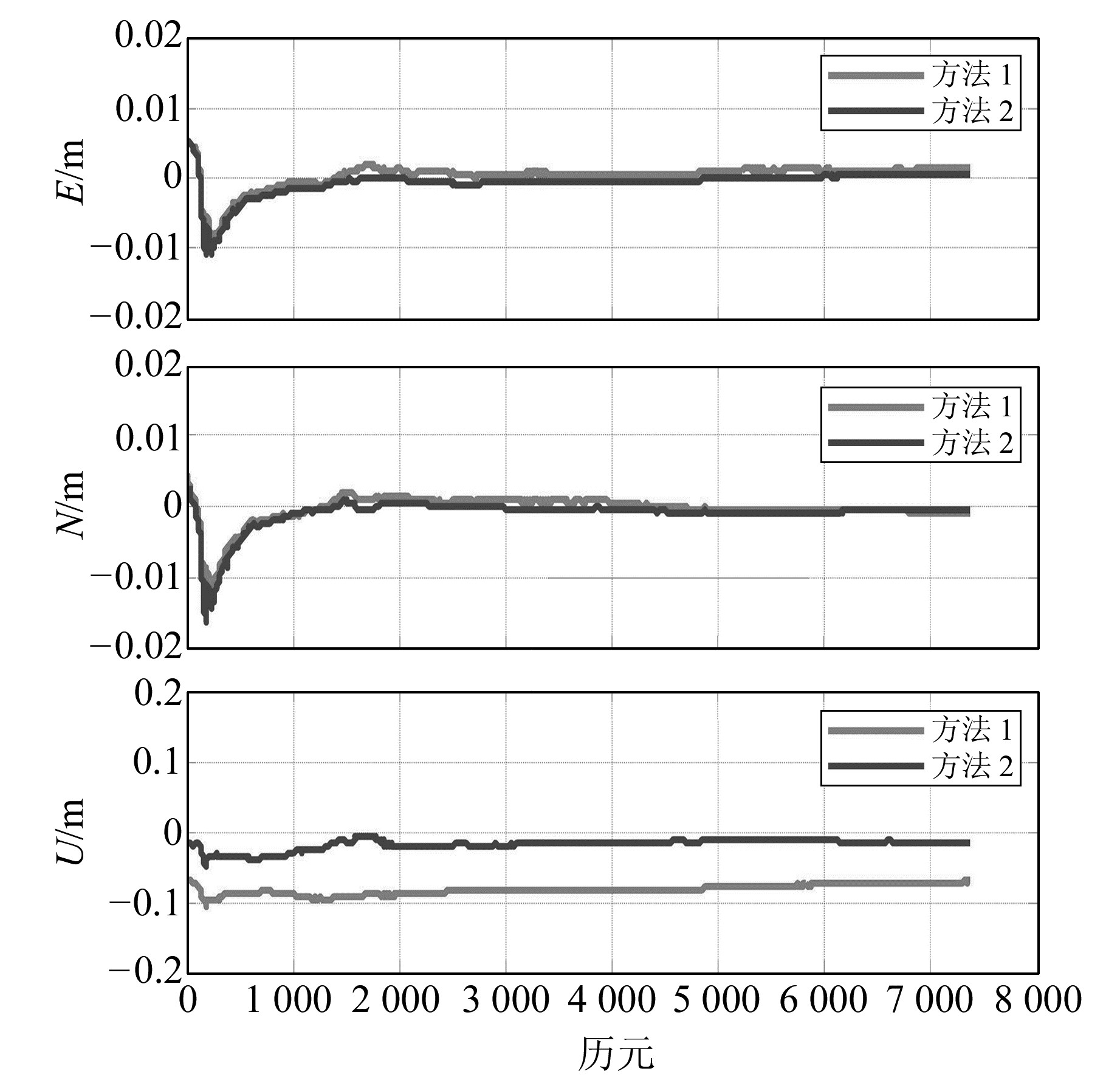
|
图 4 GPS动态监测3个方向误差序列 Fig. 4 GPS dynamic monitoring error sequence of the three directions |
为了定量分析方法2相对于方法1定位精度的提升幅度,对所有历元定位结果取平均值与GAMIT解算结果作差(表 1)。可以看出,经过对流层参数估计后,E、N 2个方向定位结果基本相同,有较小幅度的提升;而U方向定位精度则提升了约6 cm,即传统RTK双差忽略的对流层残余误差基本都被待求解的U方向坐标参数吸收了,而经过本文精确的对流层延迟参数估计并改正后,U方向定位精度也有较大的提高。
|
|
表 1 2种方法对应的平均定位误差统计 Tab. 1 Statistical average positioning errors corresponding to the two methods |
超高层建筑由于楼层较高,进行GPS动态监测时,监测站和参考站之间的空气湿度分布往往不一样,传统RTK双差模式难以完全消除对流层误差。本文介绍了一种精确的参数估计方法对残余对流层误差进行改正,实验表明,经过改正后的定位精度,尤其是在高程方向上得到显著提升。
本文验证了数据处理中有必要顾及对流层延迟影响,介绍的对流层参数估计方法也具有较好的实用性,但仍存在一些需要研究的问题,如没有考虑对流层参数和高程参数的强相关特性,也没有考虑到对流层短时间内突变的情况,如台风等恶劣天气条件下对流层参数估计中随机游走谱密度大小及实时确定等问题,是一些值得深入研究的方向。
| [1] |
Hofmann W B, Lichtenegger H, Collins J. Global Positioning System:Theory and Practice[M]. Berlin: Springer-Verlag, 2001
(  0) 0) |
| [2] |
陈永奇. 单历元GPS变形监测数据处理方法的研究[J]. 武汉测绘科技大学学报, 1998, 4(4): 324-328 (Chen Yongqi. Development of the Methodology for Single Epoch GPS Deformation Monitoring[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 4(4): 324-328)
(  0) 0) |
| [3] |
张双成, 张鹏飞, 范朋飞. GPS对流层改正模型的最新进展及对比分析[J]. 大地测量与地球动力学, 2012, 32(2): 91-95 (Zhang Shuangcheng, Zhang Pengfei, Fan Pengfei. Recent Progress and Comparative Analysis of Tropospheric Correction Models Based on GPS[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 91-95)
(  0) 0) |
| [4] |
殷海涛, 黄丁发, 熊永良, 等. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报:信息科学版, 2007, 32(5): 454-457 (Yin Haitao, Huang Dingfa, Xiong Yongliang, et al. New Model for Tropospheric Delay Estimation of GPS Signal[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 454-457)
(  0) 0) |
| [5] |
章迪, 郭际明, 陈雪丰, 等. 对流层延迟估计对高差较大短基线解算的影响[J]. 大地测量与地球动力学, 2014, 34(2): 146-149 (Zhang Di, Guo Jiming, Chen Xuefeng. Influence of Estimation of Tropospheric Delay on Short Baseline with Big Height Difference[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 146-149)
(  0) 0) |
| [6] |
李胜, 韩永亮. BDS实时动态相对定位卡尔曼滤波算法[J]. 测绘通报, 2015(5): 9-12 (Li Sheng, Han Yongliang. A Kalman Filter Algorithm for Real Time Kinematic Positioning Based on Beidou Navigation Satellite System[J]. Bulletin of Surveying and Mapping, 2015(5): 9-12)
(  0) 0) |
| [7] |
徐彦田, 程鹏飞, 蔡艳辉, 等. 估计对流层延迟的单频RTK卡尔曼滤波算法[J]. 测绘通报, 2012(8): 4-6 (Xu Yantian, Cheng Pengfei, Cai Yanhui. A Kalman Filter Algorithm for Single-Frequency RTK Solution[J]. Bulletin of Surveying and Mapping, 2012(8): 4-6)
(  0) 0) |
| [8] |
范士杰, 刘焱雄, 高兴国, 等. 海上动态GPS大气可降水量信息反演[J]. 中国石油大学学报:自然科学版, 2012, 36(3): 84-75 (Fan Shijie, Liu Yanxiong, Gao Xingguo, et al. Retrieval Method of Marine Kinematic GPS Precipitable Water Vapor[J]. Journal of China University of Petroleum:Edition of Natural Science, 2012, 36(3): 84-75)
(  0) 0) |
| [9] |
Kouba J. Testing of Global Pressure/Temperature(GPT) Model and Global Mapping Function(GMF) in GPS Analyses[J]. Journal of Geodesy, 2009, 83(3): 199-208
(  0) 0) |
| [10] |
Nelson C R, Plosser C R. Trends and Random Walks in Macro-Economic Time Series[J]. Journal of Monetary Economics, 1982, 10(2): 139-162 DOI:10.1016/0304-3932(82)90012-5
(  0) 0) |
| [11] |
Newman M E J. A Measure of Betweenness Centrality Based on Random Walks[J]. Social Networks, 2005, 27(1): 39-54 DOI:10.1016/j.socnet.2004.11.009
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37


