2. 中国科学院精密导航定位与定时技术重点实验室,西安市书院东路3号,710600;
3. 长安大学地质工程与测绘学院,西安市雁塔路126号,710054
目前,针对GPS系统,国际GNSS服务(IGS)已提供其实时轨道修正参数产品[1],且国内外多位学者已针对其产品的实时服务性能进行了分析[2-5]。对于BDS,国内外多家机构可提供其实时轨道修正参数产品,虽然整体计算思路与GPS相同,但由于BDS与GPS相比存在星座异质性以及跟踪站未全球分布等诸多现状,所以不同机构在跟踪站选取、定轨策略、预报弧段选取策略、修正参数计算方法和数据龄期选取等方面各有差异,且目前系统描述BDS实时轨道修正参数的计算方法及对其精度进行评估的相关文献较少。
基于此,本文详细给出一套BDS实时轨道修正参数的计算方法,并分析利用该方法得到的BDS实时轨道修正参数产品在产品播发基准时刻以及数据龄期内的精度,验证本文方法用于计算BDS实时轨道修正参数的可行性。
1 计算方法在高精度位置服务中,对卫星轨道进行修正的主要手段为通过高精度的卫星轨道预报产品获取其相对于广播星历计算得到的卫星轨道修正值,并将其通过网络或卫星播发给用户,用户在实时定位时便可以对广播星历计算得到的卫星轨道结果进行修正,从而提高实时定位精度。本文BDS实时轨道修正参数的计算主要分为以下2个步骤。
1) 计算BDS预报轨道。具体方法与IGS计算超快速轨道产品的方法基本相同,首先利用实测数据计算高精度的卫星轨道状态参数,然后通过轨道积分得到预报弧段轨道结果[6]。目前IGS超快速轨道产品更新频率为6 h,为了得到连续高精度的预报轨道,采用滑动窗口的方式,每1 h更新1次预报轨道。由于在实际数据处理过程中,BDS预报轨道的解算时间大致需要2 h,因此在考虑时延的情况下,选择计算轨道修正参数的弧段时,选取的是每一预报轨道弧段的2~3 h。
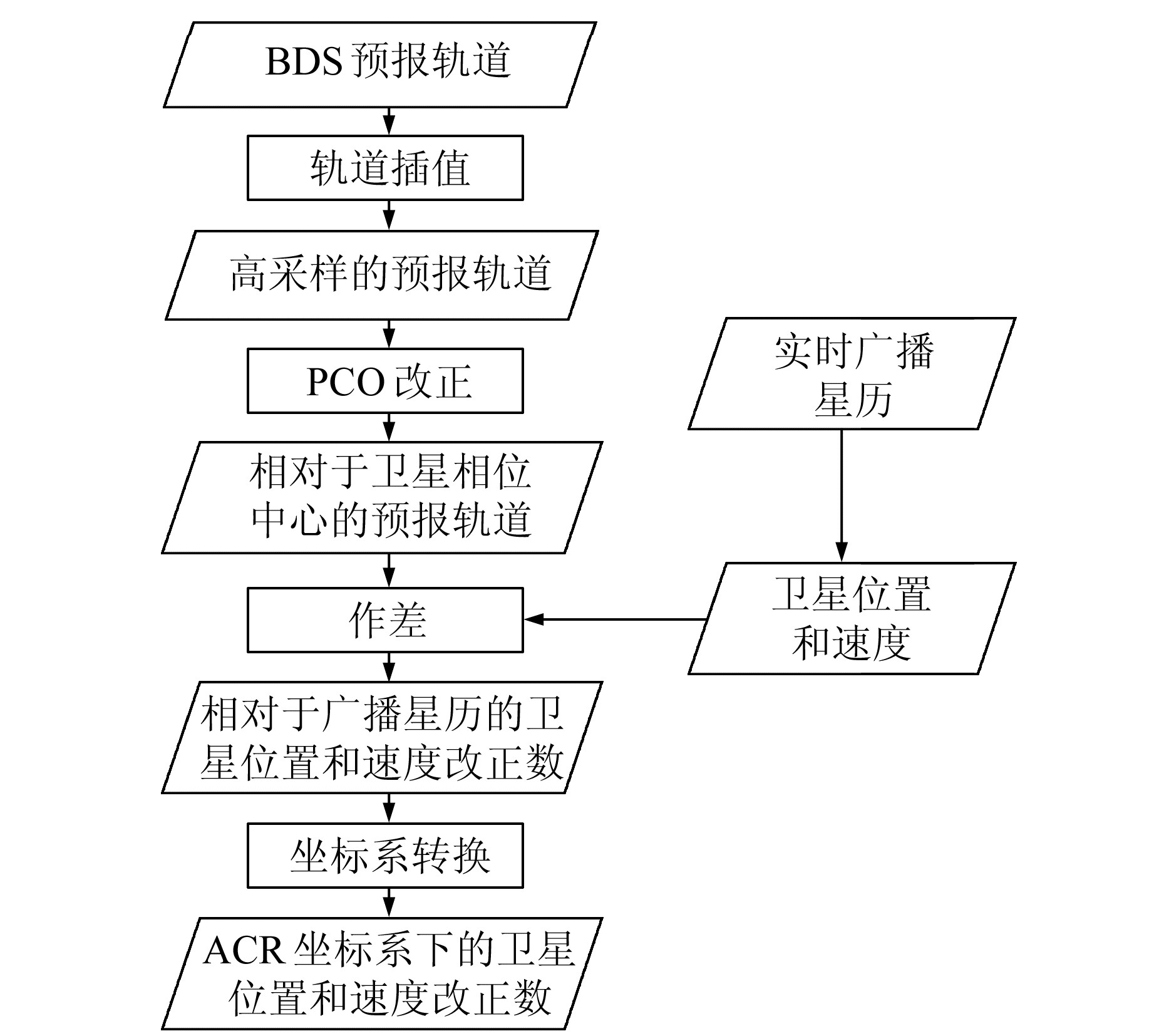
2) 计算轨道修正参数。通过预报轨道生成实时轨道修正参数的主要流程如图 1所示,关键步骤如下。
|
图 1 BDS实时轨道修正参数解算流程 Fig. 1 The calculation process of BDS real-time orbit correction parameters |
在得到预报轨道的基础上,需要重采样得到高采样率的卫星轨道值。本文采用拉格朗日9阶插值法,同时得到各基准时刻的卫星位置和速度。
PCO改正是将以卫星质心为参考的预报轨道转换到以卫星相位中心为参考的预报轨道,即
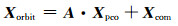
|
(1) |
式中Xcom为卫星质心的三维位置,Xpco为卫星的PCO改正信息,A为旋转矩阵,Xorbit为卫星相位中心的三维位置。
在获取广播星历在基准时刻的卫星位置和速度后进行作差,得到卫星位置修正参数,即
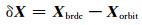
|
(2) |

|
(3) |
式中,Xbrdc为广播星历推算出的卫星位置,δX为卫星位置修正参数Vbrdc为广播星历推算出的卫星速度,Vorbit为拉格朗日插值得到的卫星速度,δV为卫星速度修正参数。
随后,需要将地固系下的卫星位置修正参数转换到卫星坐标系下,即在卫星轨道切向、法向和径向下的卫星位置修正参数。转换矩阵可按如下方法获取:
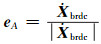
|
(4) |
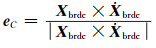
|
(5) |
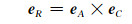
|
(6) |

|
(7) |
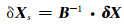
|
(8) |
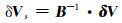
|
(9) |
式中,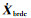
用户在使用实时轨道修正参数时,首先需匹配广播星历,然后根据如下公式即可获得修正后的卫星位置:
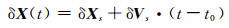
|
(10) |

|
(11) |

|
(12) |
式中,t0为轨道修正参数的基准时刻,t为需要计算的轨道修正参数的时刻,δX(t)为卫星坐标系下t时刻的位置修正参数,δXorbit(t)为地固系下t时刻的位置修正参数,Xbrdc(t)为由广播星历推算出的t时刻卫星位置,Xorbit(t)为t时刻卫星相位中心的三维位置。
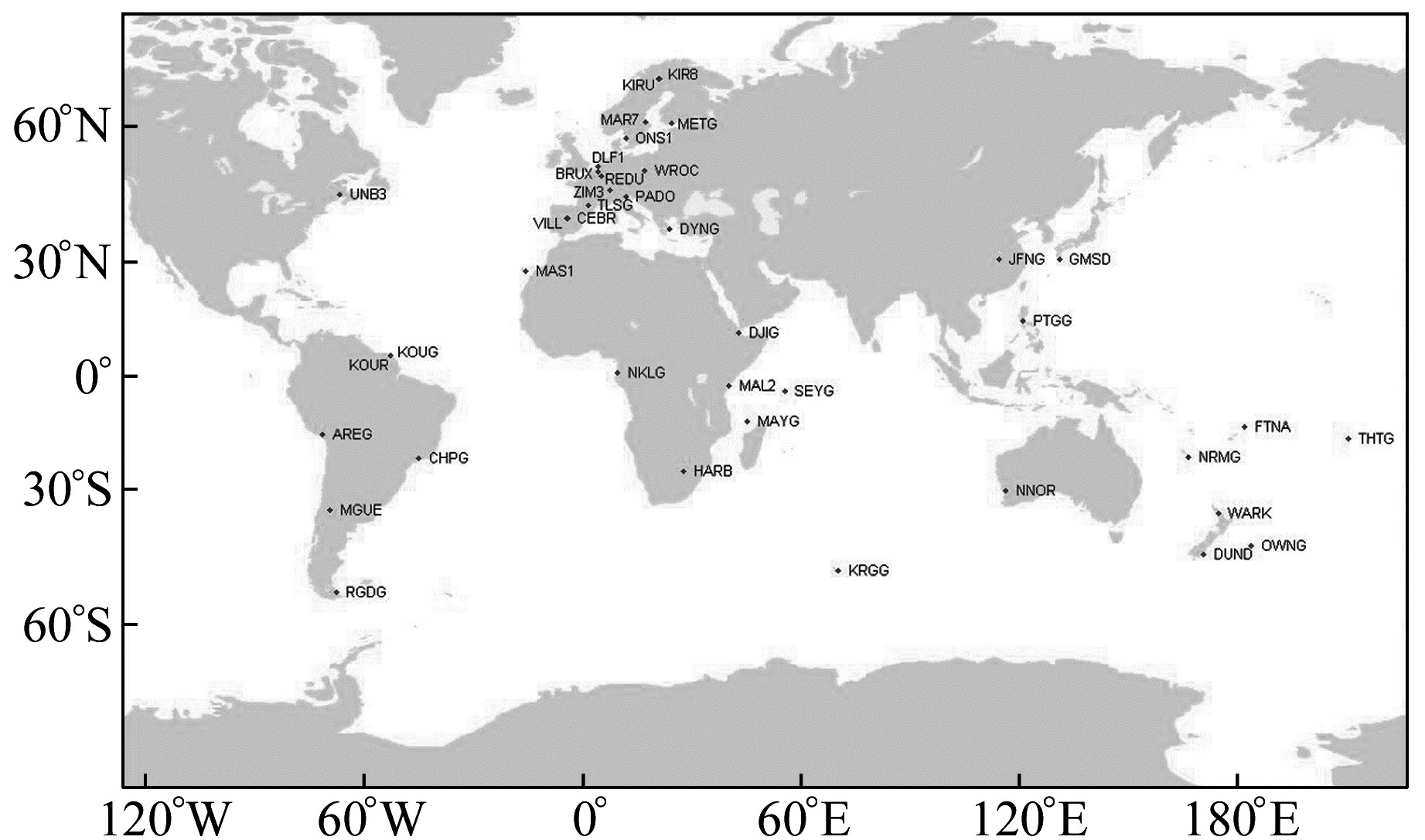
2 算例分析选取2015年年积日326~330的40个跟踪站的小时观测数据,计算24个预报轨道弧段,根据每一预报轨道弧段的2~3 h预报轨道以及广播星历,计算得到年积日330的实时轨道修正参数。跟踪站分布如图 2所示,实测部分轨道定轨策略如表 1所示。
|
图 2 定轨跟踪站分布 Fig. 2 Station distribution of orbit determination |
|
|
表 1 定轨数据处理策略 Tab. 1 Data processing strategies of orbit determination |
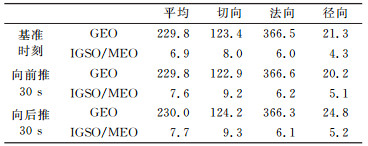
算例中轨道修正参数的播发频率设计为1 min。RTCM规定,播发的轨道修正参数的基准时刻为播发时刻加上更新频率的一半,即本文轨道修正参数的基准时刻为每分钟的30 s,数据龄期也为30 s。因此,为了分析本文方法得到的实时轨道修正参数的精度及其衰减性,利用GFZ的轨道产品分别评价利用实时轨道修正参数恢复得到的基准时刻的轨道、由各基准时刻向前推30 s的轨道以及由各基准时刻向后推30 s的轨道精度。各弧段实时轨道精度时间序列结果如图 3、4所示,所有弧段实时轨道精度中位数统计如表 2(单位cm)所示。

|
图 3 GEO卫星平均精度序列 Fig. 3 The average precision sequence of GEO satellites |

|
图 4 IGSO/MEO卫星平均精度序列 Fig. 4 The average precision sequence of IGSO and MEO satellites |
|
|
表 2 实时轨道修正参数精度统计 Tab. 2 The statistics of real-time orbit correction parameters precisions |
由图 3和表 2可以看出,GEO卫星在通过修正参数外推30 s后,轨道精度与基准时刻轨道精度相当,切向、法向、径向及其平均精度并非均有所降低,个别时段外推轨道精度甚至优于基准时刻轨道精度,这主要是由于目前GEO卫星定轨精度较低所致。其定轨精度较低的原因主要是由于GEO卫星高轨且静地的特性使其与跟踪站间的几何结构较差,导致卫星钟差与卫星轨道状态参数间的相关性较大;此外,GEO采用零偏姿态控制模式[11],卫星姿态模型与GPS卫星有较大差距,如果将GPS卫星的光压摄动模型应用到GEO卫星上,将导致GEO卫星动力学模型与实际偏差较大,继而影响GEO卫星最终的定轨精度。
由表 2可以看出,GEO卫星定轨精度切向明显优于法向,这除了上述描述的GEO卫星定轨精度较低的原因外,还由于本文评估精度时标准轨道选取GFZ公布的BDS事后轨道、定轨时跟踪站选取不同以及定轨策略不同,对GEO卫星定轨精度影响较大。
由图 4及表 2可以看出,IGSO卫星和MEO卫星在通过修正参数外推30 s后,轨道切向、法向、径向及其平均精度均有所降低,但轨道精度衰减较少,在1 cm左右。综合看,IGSO卫星和MEO卫星实时轨道修正参数在数据龄期内的轨道平均精度优于8 cm,其中径向精度约5 cm,基本可满足实时高精度定位需求。
3 结语本文给出一种BDS实时轨道修正参数的计算方法,分析了利用该方法得到的BDS实时轨道修正参数的精度及其在数据龄期内的衰减情况,主要结论如下。
1) 本文给出的计算方法可以较好地完成BDS实时轨道修正参数的解算。
2) 利用本文方法得到的BDS实时轨道修正参数的精度在数据龄期内并没有明显衰减,基本可满足实时高精度用户需求。
3) 本文方法还不能实时探测并发现卫星轨道机动,需后续进一步研究完善。
致谢: 感谢全球连续监测评估系统(iGMAS)以及MGEX跟踪站网络提供数据,感谢德国地学研究中心葛茂荣教授对本文提供的支持。
| [1] |
Caissy M, Agrotis L, Weber G, et al. Coming Soon: The International GNSS Real-Time Service[EB/OL]. www. gpsworld. com, 2012
(  0) 0) |
| [2] |
尹倩倩, 楼益栋, 易文婷. IGS实时产品比较与分析[J]. 大地测量与地球动力学, 2012, 32(6): 123-128 (Yin Qianqian, Lou Yidong, Yi Wenting. Comparison and Analysis of IGS Real-Time Product[J]. Journal of Geodesy and Geodynamics, 2012, 32(6): 123-128)
(  0) 0) |
| [3] |
Hadas T, Bosy J. IGS RTS Precise Orbits and Clocks Verification and Quality Degradation Over Time[J]. GPS Solutions, 2015, 19(1): 93-105 DOI:10.1007/s10291-014-0369-5
(  0) 0) |
| [4] |
Elsobeiey M, Harbi S. Performance of Real-Time Precise Point Positioning Using IGS Real-Time Service[J]. GPS Solutions, 2016, 20(3): 565-571 DOI:10.1007/s10291-015-0467-z
(  0) 0) |
| [5] |
臧建飞, 范世杰, 秦学斌, 等. IGS RTS产品数据中段修复方法研究[J]. 大地测量与地球动力学, 2016, 36(10): 884-888 (Zang Jianfei, Fan Shijie, Qin Xuebin. Research on Repairing Method for the Data Interruptions of IGS RTS Products[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 884-888)
(  0) 0) |
| [6] |
张睿. BDS精密定轨关键技术研究[D]. 西安: 长安大学, 2016 (Zhang Rui. Research on Key Technologies of BDS Precise Orbit Determination[D]. Xi'an: Chang'an University, 2016) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01113996
(  0) 0) |
| [7] |
Beutler G, Brockmann E, Gurtner W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Results[J]. European Respiratory Journal, 1994, 7(7): 1-1 364
(  0) 0) |
| [8] |
He L N, Ge M R, Wang J X, et al. Experimental Study on the Precise Orbit Determination of the Beidou Navigation Satellite System[J]. Sensors, 2013, 13(3): 2-2 928 DOI:10.1109/JSEN.2013.2251989
(  0) 0) |
| [9] |
Dilssner F, Springer T, Schoenemann E, et al. Estimation of Satellite Antenna Phase Center Corrections for Beidou[C]. IGS Network, Data and Analysis Center Workshop, California, 2014
(  0) 0) |
| [10] |
黄观文, 张睿, 张勤, 等. BDS卫星天线相位中心改正模型比较[J]. 大地测量与地球动力学, 2015, 35(4): 658-661 (Huang Guanwen, Zhang Rui, Zhang Qin, et al. Comparison and Analysis of Different Models of Antenna Phase Center Correction of BDS Satellites[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 658-661)
(  0) 0) |
| [11] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014 (Guo Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm
(  0) 0) |
2. Key Laboratory of Precision Navigation and Timing Technology, CAS, 3 East-Shuyuan Road, Xi'an 710600, China;
3. College of Geology Engineering and Geomatics, Chang'an University, 126 Yanta Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37