2. 武汉大学地球空间信息技术协同创新中心,武汉市珞喻路129号,430079
北斗卫星导航系统(Beidou navigation satellite system,BDS)是中国正在建设的独立运行的全球卫星导航系统。2012年底,北斗系统宣布已实现亚太地区的导航定位授时服务[1]。目前,提供服务的北斗在轨卫星共有14颗,分别为5颗GEO(geostationary earth orbit)卫星,6颗IGSO(inclined geosynchronous satellite orbit)卫星和3颗MEO(medium earth orbit)卫星。按照“三步走”战略,北斗卫星导航系统目前正处于第三步,即在2020年左右建成由5颗静止轨道卫星和30颗非静止轨道卫星组成的覆盖全球的北斗卫星导航系统[2-3]。北斗三期试验卫星作为北斗卫星导航系统全球组网工作的重要组成部分,于2015-03~2016-02先后发射了C31(IGSO)、C32(IGSO)、C33(MEO)、C34(MEO)、C35(MEO)5颗卫星,以便开展全球星座在轨测试和验证工作。卫星精密轨道和钟差作为导航卫星核心产品,是进行其他科学研究及导航定位的基础条件。针对北斗三期试验卫星的精密定轨和定位,国内学者展开了相关研究。Tan等[4]利用9个iGAMS(international GNSS monitoring and assessment system)测站测定了4颗试验星的精密轨道,IGSO和MEO重叠弧段径向RMS分别为10 cm和40 cm,切向为25 cm和60 cm;陈金平等[5]评估了北斗三期试验星星间伪距测量对卫星轨道和钟差的影响,采用星地间联合定轨重叠弧段径向精度优于0.1 m,三维位置精度优于0.5 m,预报24 h径向精度优于0.2 m,三维位置精度优于1 m,较区域监测网L波段定轨结果有较大提升;Zhang等[6]对北斗三期卫星信号特征及定位的研究表明,北斗三期卫星的加入可提高整周模糊度的固定率,从而提高相对定位的精度。
为进一步研究北斗三期试验卫星在轨特性,本文基于多个观测网的实测数据,利用武汉大学自主研制的卫星导航数据综合处理软件PANDA[7-9],确定包含二期卫星和三期试验星在内的所有在轨北斗卫星精密轨道和钟差产品,并基于轨道重叠弧段比较和人卫激光测距检核等对计算轨道精度进行评估,然后利用精密单点定位分析试验星对当前北斗系统定位性能的影响。
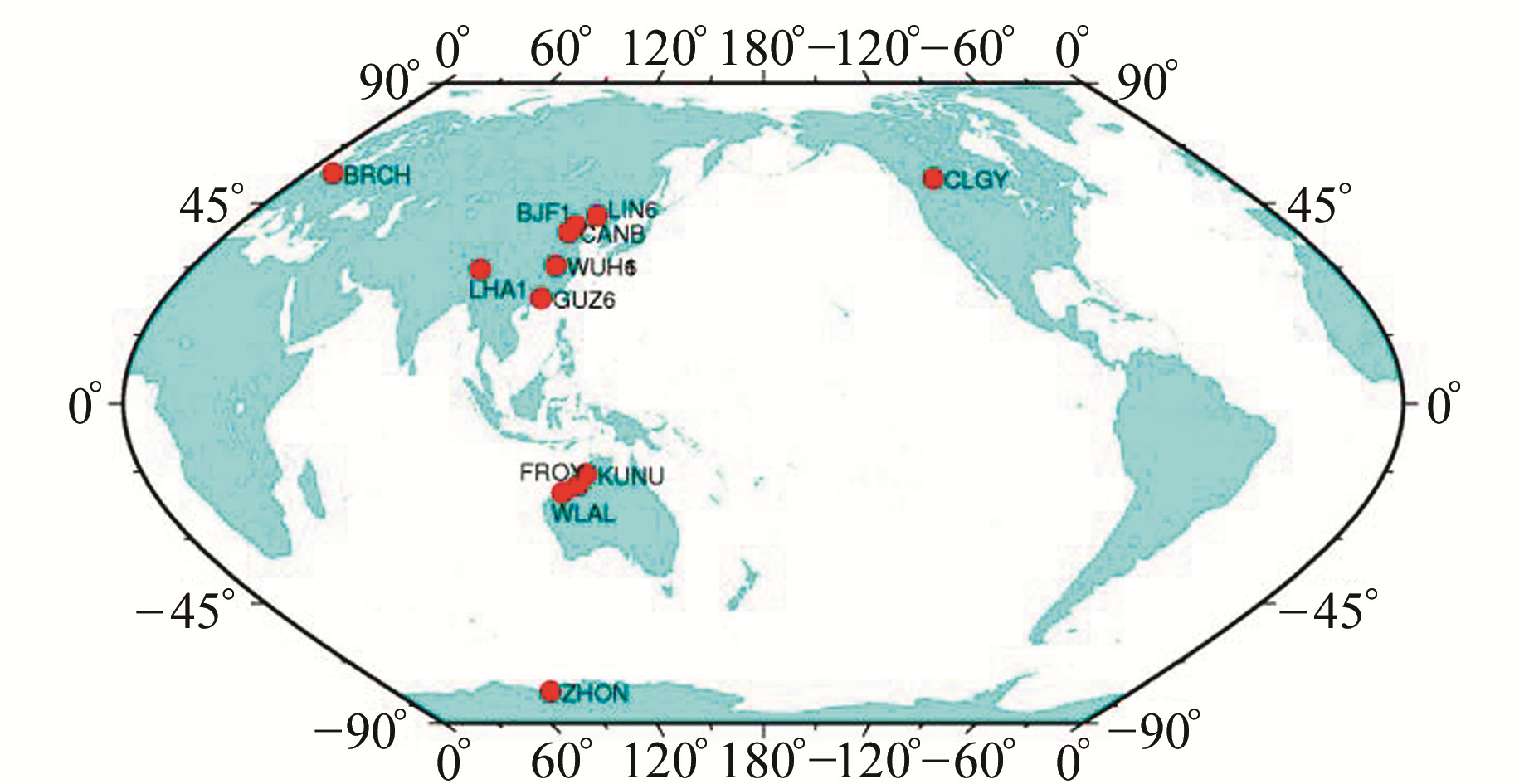
1 精密定轨 1.1 数据来源及精密定轨策略数据来源为iGMAS、武汉大学BETN(Beidou experimental tracking network)网以及IGS MGEX等13个测站的观测数据(图 1),观测时间为2016-08-27~2016-09-21(年积日240~265)。
|
图 1 定轨地面测站分布 Fig. 1 Tracking stations in precise orbit determination for Beidou satellites |
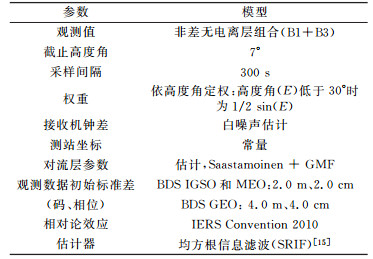
考虑到当前跟踪北斗三期试验卫星的测站较少,且绝大多数位于亚太地区,本文定轨采用“两步法”[10],定轨弧段为3 d(72 h)。首先利用武汉大学提供的GPS卫星最终精密星历和300 s钟差产品对上述测站进行精密单点定位(PPP),确定地面站的站坐标、接收机钟差、天顶对流层参数;然后将所得参数作为已知值引入,进行北斗卫星定轨。由于此时间段内不存在C35卫星的观测数据,因此本文定轨及钟差确定不包括C35卫星。解算参数包括参考时刻卫星位置和速度、卫星钟差、系统间偏差、5个光压参数[11]和1个切向经验力参数[12-13]。此外,考虑到三期试验卫星没有B2信号,因此选择B1和B3频点的数据组成无电离层组合观测值,同时确定北斗二期在轨卫星和三期试验卫星轨道和钟差。定轨过程中采用的观测模型和力模型如表 1所示。
|
|
表 1 定轨观测模型与力模型 Tab. 1 Observation and force model for POD |
重叠弧段比较是轨道内符合精度检核的常用方法。本文定轨弧长为3 d,采用弧段1最后一天的轨道与弧段2中间一天的轨道进行比较。表 2(单位cm)给出北斗三期试验卫星3个方向重叠弧段统计结果。可以看出,切向的RMS最大,精度在20~33 cm,法向优于20 cm,径向优于7 cm,IGSO 3个方向的平均精度为25.9 cm、15.1 cm、6.0 cm,MEO为22.6 cm、14.2 cm、5.2 cm,可见MEO卫星重叠精度略优于IGSO卫星。在轨北斗二期卫星相应轨道重叠精度统计结果见表 2。整体而言,切向精度在10~31 cm,平均精度为23.4 cm,法向优于20 cm,平均为15.9 cm,径向优于8 cm,平均为5.7 cm。从定轨结果来看,在采用相同测站分布的条件下,北斗三期试验星和北斗二期在轨工作卫星的轨道重叠弧段精度相当。
|
|
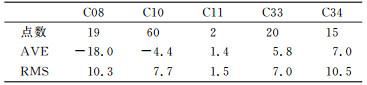
表 2 北斗卫星24 h重叠弧段RMS值 Tab. 2 Averaged daily RMS values of 24 h orbit overlap differences |
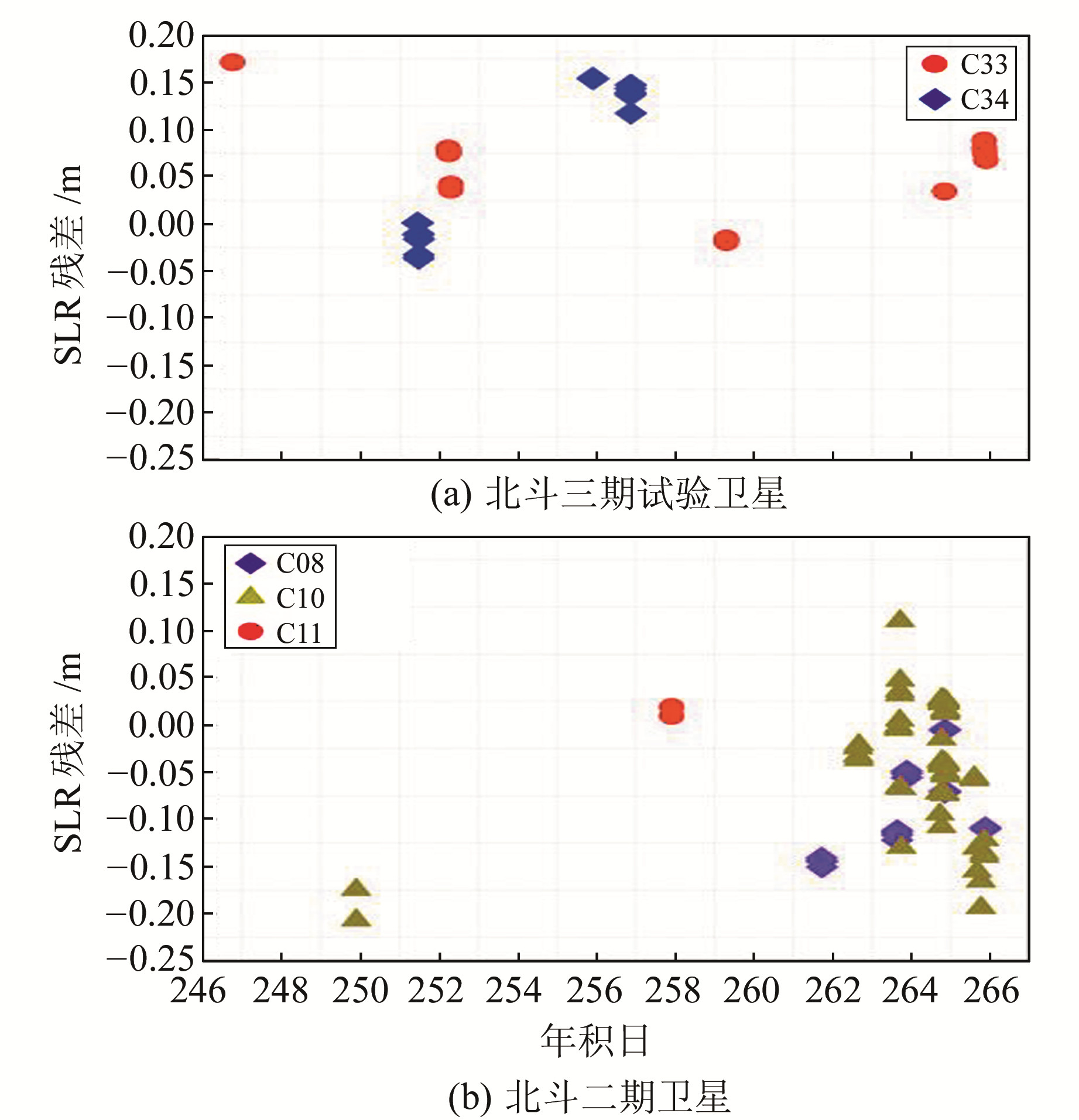
由于精度高,人卫激光测距(satellite laser ranging,SLR)检核是目前评定轨道绝对精度最有力的手段。SLR检核残差是轨道误差在人卫激光站视线方向上的投影,主要反映轨道的径向误差。本文SLR检核的轨道段为每个定轨弧段中间一天的弧段,二期和三期试验卫星相应SLR残差序列如图 2所示,其相应统计值见表 3(单位cm)。总体来说,北斗三期试验卫星的SLR检核精度和北斗二期在轨工作卫星精度相当,平均为8.9 cm,与重叠弧段反映的径向轨道精度在同一量级。
|
图 2 北斗卫星SLR检核残差序列 Fig. 2 The series of SLR residuals of Beidou satellites |
|
|
表 3 北斗卫星SLR检核残差统计 Tab. 3 SLR residuals for Beidou satellites |
为分析北斗三期试验卫星对精密定位的影响,并验证现有北斗在轨星座的定位性能,本文研究在加入北斗三期试验卫星前后对精密单点定位的影响。为了得到独立的验证结果,选取BETN网中未参与北斗卫星轨道和钟差确定的测站SHH6(121°E,31°N)进行静态精密单点定位。处理时段为2016-09-07~2016-09-21(年积日251~265)共15 d,数据处理时长为24 h,数据处理间隔为300 s,观测模型和解算参数如表 4所示[14]。
|
|
表 4 PPP观测模型及解算参数 Tab. 4 Observation model andparameter for PPP |
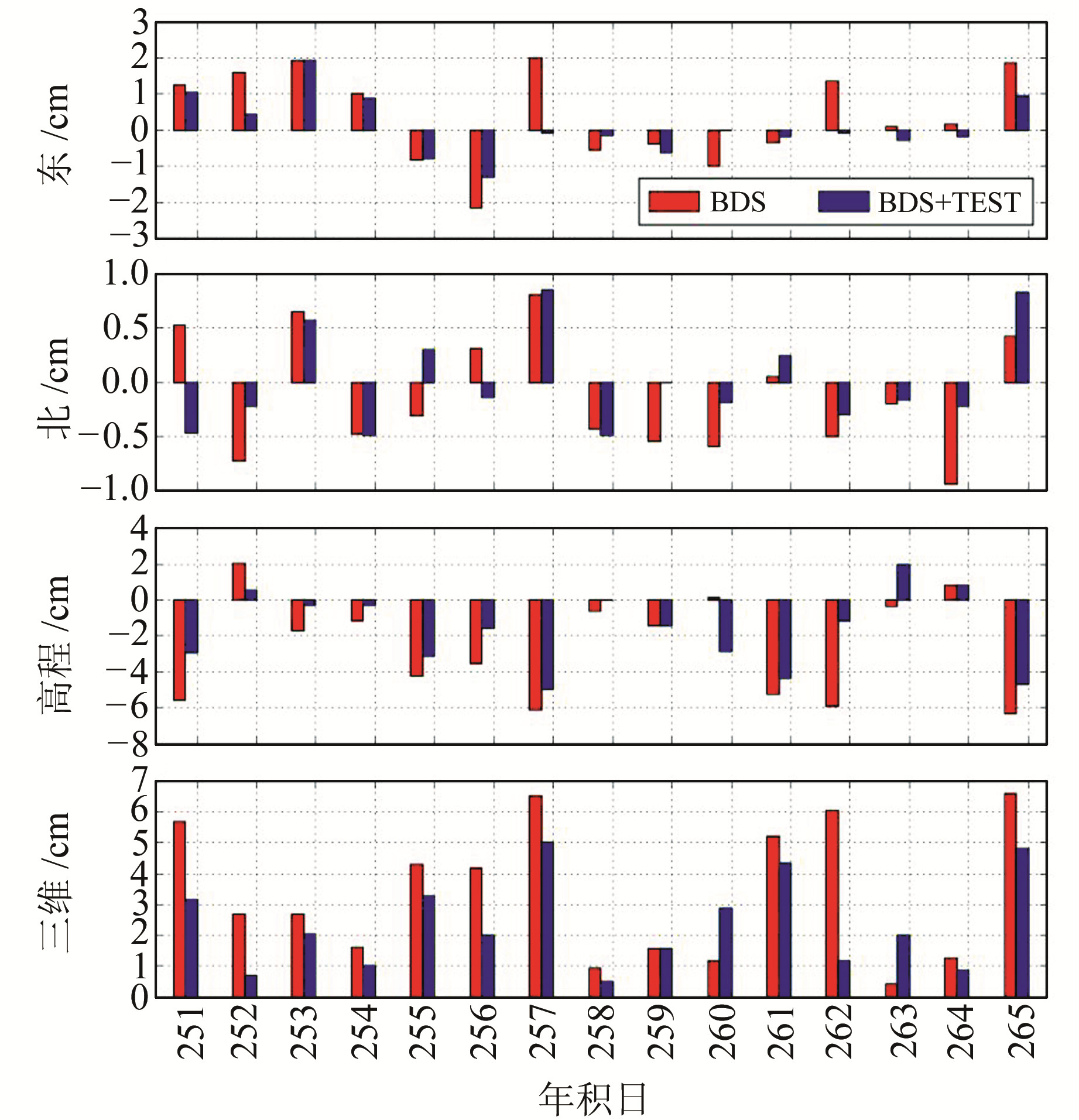
由于上述测站可接收到GPS、BDS等至少2个系统的观测值,因此将GPS双频观测值计算的坐标(15 d的平均值)作为上述测站坐标的参考值。本文分别计算2类PPP结果,其一仅采用北斗二期卫星(BDS),其二采用所有北斗在轨卫星,即二期和三期试验星(BDS+TEST)。图 3所示序列为SHH6站2种定位结果的单天坐标值与参考值在东、北和高程3个方向的坐标差,相应统计结果如表 5(单位cm)所示。统计时,如果某一历元三维定位误差小于10 cm且该历元后10个历元的定位误差同样满足该阈值,则视该历元时刻为收敛时刻,并以此统计相应收敛时间。由于静态处理随着数据累积定位精度逐步提升,因此将弧段最后一个历元结果作为测站坐标最优估值,并统计其精度[14]。
|
图 3 SHH6测站2种静态PPP结果与参考坐标之差 Fig. 3 Coordinate differences of daily static PPP solutions with reference for station SHH6 |
|
|
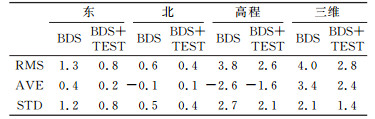
表 5 2种静态PPP结果与参考坐标之差RMS值 Tab. 5 The RMS、average and STD of coordinate differences |
由图 3和表 5可以看出,北斗系统精密单点定位单天解与参考坐标之差在东、北、高程3方向的RMS分别为1.3 cm、0.6 cm和3.8 cm,三维位置RMS为4.0 cm;在加入北斗三期试验星后,除个别天数外,精度在3个方向均有不同程度的提高,东、北、高程3个方向的RMS值达到0.8 cm、0.4 cm和2.6 cm,三维位置RMS为2.8 cm,相对于单北斗二期,3个方向分别提高0.5 cm、0.2 cm和1.2 cm,三维提高1.2 cm,同时3个方向及三维位置的标准差(STD)也有所下降。从图 5可知,年积日260和263在加入试验星后,高程方向误差增加,导致三维定位误差变大,其主要原因是这2 d的C31卫星定轨精度较差,影响定位结果。去掉该卫星重新计算PPP,可以明显减小高程方向的误差,可使定位结果优于单北斗二期的定位结果。
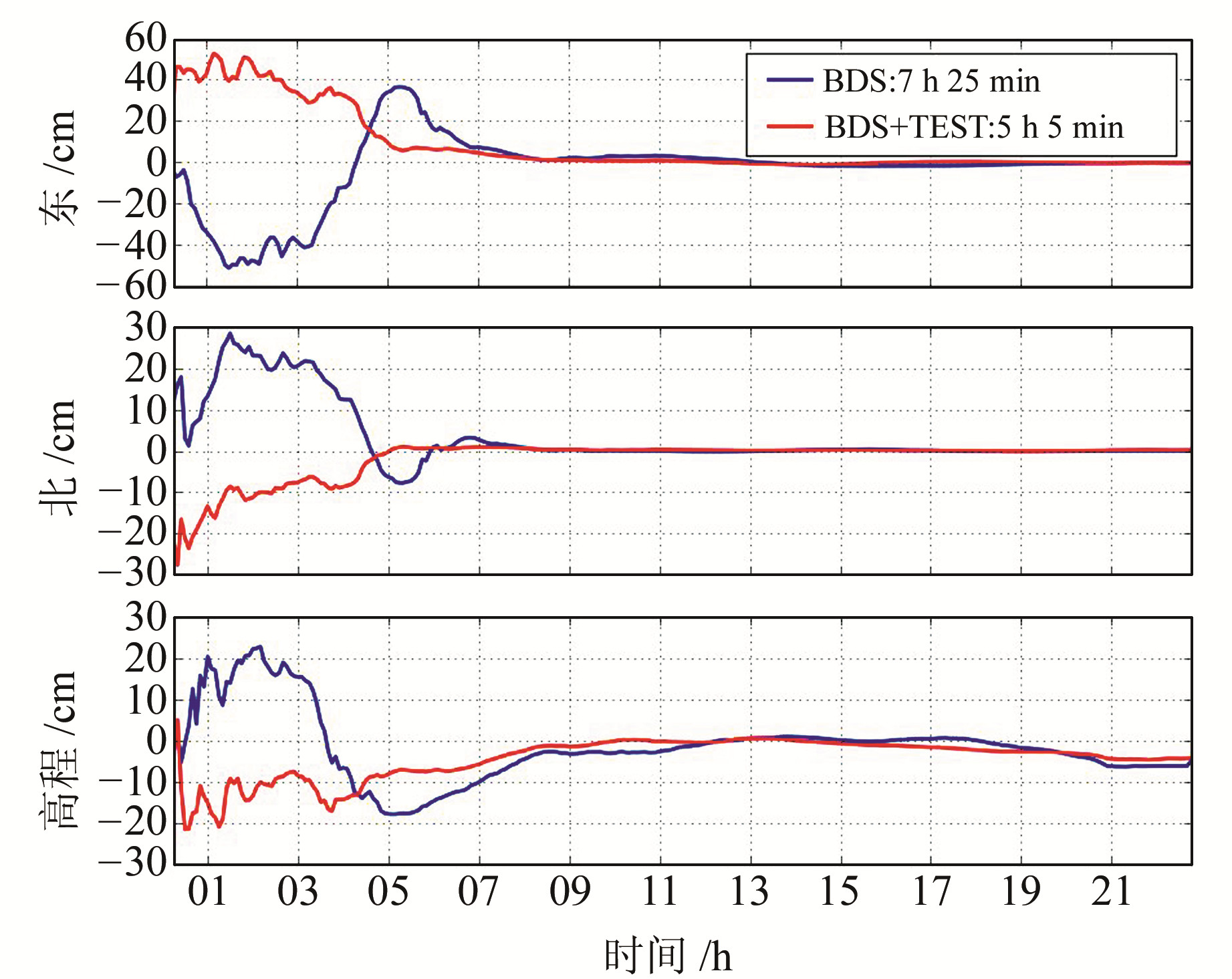
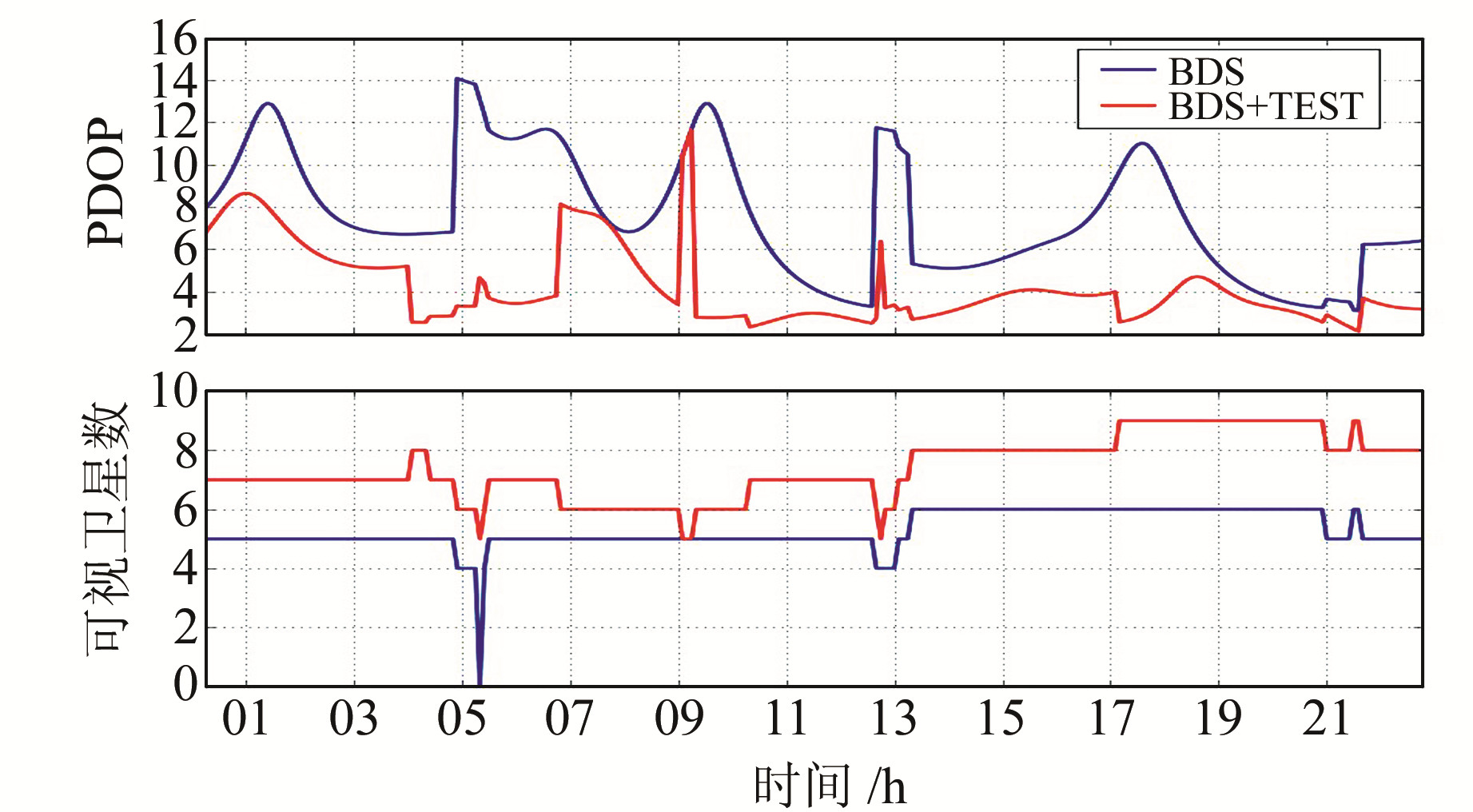
将测站坐标参数在参数估计过程的每个解算历元输出其结果,可以直观地显示其收敛时间,比较收敛速度。图 4为SHH6站年积日261增加北斗三代试验卫星前后2种PPP 3个方向收敛时间的对比。结果表明,在相同数据处理策略下,在加入试验星后,3个方向的收敛速度都有所提高,测站位置收敛时间由7 h 25 min变为5 h 5 min,缩短了2 h 20 min。其主要原因是在加入试验星后,该测站上的可视卫星数明显增加,使空间位置精度衰减因子(PODP)减小(图 5),每个历元可视卫星数相比单北斗二期多2~3颗,PDOP的均值也由7.5降低到4.2,明显改善了北斗卫星的空间分布情况,从而使定位结果精度有所提高。表 6统计了15 d PPP结果的收敛时间均值,可见北斗三期试验星的加入,极大地缩短了PPP结果的收敛时间,平均缩短2 h 35 min。
|
图 4 SHH6站静态PPP收敛时间 Fig. 4 The convergence time in static PPP for station SHH6 |
|
图 5 SHH6站年积日261可视卫星数及PDOP Fig. 5 Visible satellite numbers and PDOP for SHH6 in DOY 261 |
|
|
表 6 SSH6站静态PPP平均收敛时间 Tab. 6 The mean of convergence time in static PPP for station SHH6 |
本文基于北斗三期试验卫星的实测数据,利用武汉大学自主研发的PANDA软件,确定了三期试验卫星的精密轨道。结果表明,IGSO径向重叠弧段精度优于7.0 cm,MEO优于5.3 cm,三维精度可达29.7 cm,与同时解算的北斗二期在轨非GEO卫星精度相当,表明三期试验卫星质量较高。由于计算的北斗三期试验卫星轨道未涉及地影时期,因此对于北斗三期与二期卫星在地影期间及进出地影段的姿态控制、光压模型等方面的区别可作进一步研究。
比较分析可知,基于以上确定的北斗二期在轨卫星和三期试验星轨道及钟差进行精密单点定位,在加入三期试验卫星后,可达平面优于1.0 cm、高程2.6 cm的精度,较单北斗二期定位精度在平面上平均提高0.5 cm,高程提高1.1 cm,同时使得PPP的收敛时间明显缩短。以上结果仅是在有限的测站及数据下试验分析所得,随着试验卫星的长期运行以及三期卫星数量和地面跟踪站的不断增加,相应的轨道精度和PPP能力将更值得期待。
| [1] |
中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件1. 0[R]. 北京, 2012 (China Satellite Navigation System Management Office. Beidou Satellite Navigation System Spatial Signal Interface Control File 1. 0[R]. Beijing, 2012)
(  0) 0) |
| [2] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/BDS Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [3] |
杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1-1 740 (Yang Yuanxi, Li Jinlong, Xu Junyi, et al. Contribution of the Compass Satellites Navigation System to Global PNT Users[J]. Chinese Sci Bull, 2011, 56(21): 1-1 740)
(  0) 0) |
| [4] |
Tan B, Yuan Y, Wen M, et al. Initial Results of the Precise Orbit Determination for the New-Generation Beidou Satellites (Beidou-3) Based on the iGMAS Network[J]. ISPRS International Journal of Geo-Information, 2016, 5(11): 196 DOI:10.3390/ijgi5110196
(  0) 0) |
| [5] |
陈金平, 胡小工, 唐成盼, 等. 北斗新一代试验星轨道钟差精度初步分析[J]. 中国科学:物理学 力学 天文学, 2016, 46(11) (Chen Jinping, Hu Xiaogong, Tang Chengpan, et al. Orbit Determination and Time Synchronization for New-Generation Beidou Satellites: Prelininary Results[J]. Sci Sin-Phys Mech Asrton, 2016, 46(11))
(  0) 0) |
| [6] |
Zhang X, Wu M, Liu W, et al. Initial Assessment of the COMPASS/Beidou-3: New-Generation Navigation Signals[J]. Journal of Geodesy, 2017, 91(10): 1-1 240
(  0) 0) |
| [7] |
Liu J, Ge M. PANDA Software and Its Preliminary Result of Positioning and Orbit Determination[J]. Wuhan University Journal of Natural Sciences, 2003, 8(2B): 603-609
(  0) 0) |
| [8] |
赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004 (Zhao Qile. Research on Precision Orbit Determination Theory and Software of both GPS Naviagation Constellation and LEO Satellites[D]. Wuhan: Wuhan University, 2004) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whchkjdxxb200504029
(  0) 0) |
| [9] |
Shi C, Zhao Q, Lou Y. Recent Development of PANDA Software in GNSS Data Processing[C]. Proc SPIE, Wuhan, 2008
(  0) 0) |
| [10] |
李敏, 赵齐乐, 葛茂荣. GIOVE-A卫星精密定轨仿真研究[J]. 武汉大学学报:信息科学版, 2008, 33(8): 818-820 (Li Min, Zhao Qile, Ge Maorong. Simulation Research on Precise Orbit Determination for GIOVE-A[J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 818-820)
(  0) 0) |
| [11] |
Springer T, Beutler G, Rothacher M. A New Soloar Radiation Presscve Model for GPS Satellites[J]. GPS Solutions, 1999, 1(2): 50-62
(  0) 0) |
| [12] |
Guo J, Xu X, Zhao Q, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159 DOI:10.1007/s00190-015-0862-9
(  0) 0) |
| [13] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014 (Guo Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm
(  0) 0) |
| [14] |
Zhao Q, Wang C. Assessment of the Contribution of Beidou GEO, IGSO, and MEO Satellites to PPP in Asia-Pacific Region[J]. Sensors, 2015, 15(12): 29-29 983
(  0) 0) |
| [15] |
赵齐乐, 刘经南, 葛茂荣, 等. 均方根信息滤波和平滑及其在低轨卫星星载GPS精密定轨中的应用[J]. 武汉大学学报:信息科学版, 2006, 31(1): 12-15 (Zhao Qile, Liu Jingnan, Ge Maorong, et al. Applications of Square Root Information Filtering and Smoothing on Orbit Determination of LEO Satellites with On-Board GPS Data[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 12-15)
(  0) 0) |
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37