2. 大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
通常卫星和接收机在前后历元正常的情况下,模糊度具有时不变性,采用滤波手段可以提高模糊度固定的成功率。而GLONASS卫星采用频分多址(frequency division multiple access,FDMA)技术组成双差观测方程后,因不同卫星的波长不一致,模糊度失去整数特性[1]。考虑GLONASS系统特殊性,传统方法将其双差模糊度浮点解分解为整数的双差模糊度和参考卫星站间单差模糊度,此时观测方程存在秩亏问题,需要利用码观测解算参考卫星的站间单差模糊度。GLONASS系统还存在频间偏差问题,对双差观测方程进行卡尔曼滤波处理时要特别处理GLONASS系统,并解决滤波过程中较复杂的换星问题。Wanniger[1]研究了GLONASS接收机不同天线的相位频间偏差关系。张宝成等[2]基于单差模糊度模型,提出了一种无需变换参考星的GNSS单基线卡尔曼滤波算法。
针对上述问题,本文基于多模GNSS站间单差模型给出了一种新的双差模糊度解算策略。该算法采用自适应0-1选权滤波直接解算稳定的站间单差模糊度浮点解,并通过选择基准卫星实现双差模糊度的固定。由于卫星的站间单差模糊度可分别解算,因此不用考虑滤波中的换星问题,方便进行滤波处理,同时也避免了GLONASS系统卫星波长不一致造成的双差模糊度失去整数特性或双差模糊度分解后的秩亏问题。最后利用实测数据进行验证,结果表明新算法可快速得到稳定的站间单差模糊度浮点解,提高了双差模糊度固定的成功率。
1 基于站间单差的模糊度固定原理

|
(1) |
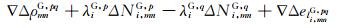
|
(2) |
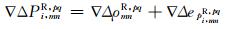
|
(3) |
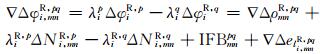
|
(4) |
式中,G为GPS系统,R为GLONASS系统,p为共视卫星,q为任意选定的参考卫星,m和n为同步测站,i为频率(i=1, 2, 3),P为码观测值,φ为相位观测值,ρ为包含基线参数的站星几何距离,N为整周模糊度,ep和el为包含多路径效应的码和相位噪声,∇Δ为星站双差运算符号, Δ为站间单差运算符号。对于GPS系统,由于其卫星间波长一致,站间单差模糊度可以合并为双差模糊度。但对于GLONASS系统,λip和λiq并不相等,若将λipΔNi, mnp-λiqΔNi, mnq分解为整数的双差模糊度和参考卫星站间单差模糊度,则观测方程会出现秩亏,若将其合并成为一个参数,则失去了模糊度的整数特性。IFB为GLONASS双差后的频间偏差,Wanniger[1]指出其在相同的天线类型时影响并不明显,但若是不同天线类型时,需要考虑其影响。GLONASS相位观测值频间偏差是与频率成正比关系的,可表示为:
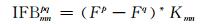
|
(5) |
式中,F对应卫星的载波频率索引值,Kmn为m、n2台接收机的频间偏差系数。不同接收机Kmn的先验值如表 1所示。
|
|
表 1 不同接收机频间偏差系数 Tab. 1 Coefficients of IFB in different receivers |
GLONASS频间偏差修正后,接收机频间偏差参数非常小,不影响模糊度固定,2个系统站间单差观测方程可统一写为[5]:
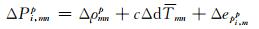
|
(6) |
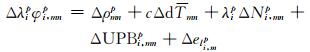
|
(7) |
其中,

|
(8) |
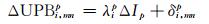
|
(9) |
式中,Δ为站间单差运算符号,dT为接收机钟差,Ip为接收机初始相位偏差,Bp为码延迟,c为光速,δ为接收机码和相位硬件延迟之差。式(7)可改写为:
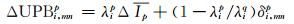
|
(10) |
式中,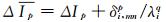
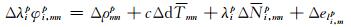
|
(11) |
式中,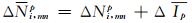
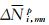
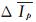
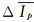
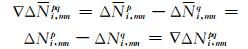
|
(12) |
此外,对于不同类型的接收机,若考虑更严密的形式,还需估计初始相位偏差的残余部分,仅从固定双差模糊度方面,可以暂不考虑。站间单差模糊度虽然包含了接收机间初始相位偏差,但其独立可估,选基准模糊度组成双差模糊度后便可消除,可直接用LAMBDA方法搜索固定双差模糊度。如果使用相同的基准进行卡尔曼滤波,前后历元均包含了相同的“基准”单差模糊度,此时模型不再需要基准卫星发生周跳后的复杂的换星映射计算问题,处理方式较为简便。但为充分利用模糊度的时不变性特点,本文基于选权滤波算法设计新的方案,以提高站间单差模糊度浮点解的精度和双差模糊度的固定成功率。
2 自适应0-1选权滤波器 2.1 数学模型文献[6]基于等价权原理提出了自适应选权滤波算法(0-1选权滤波)以解决实际应用中的状态参数出现异常的问题。其主要思想为:按照一定标准将状态参数分为正常和异常两类,正常参数表示状态参数和载体实际状态信息较为吻合,异常参数表示状态参数和实际运动状态明显不符。针对站间单差模糊度参数的特点,本文将模糊度参数分为正常和异常两种情况。当卫星消失以及发生周跳或观测值存在粗差时,模糊度参数发生异常,需要重新计算整周模糊度参数,以保证滤波器的稳定性与合理性,提高模糊度固定的成功率。
线性化后的自适应0-1选权滤波的观测方程和状态方程为[7]:
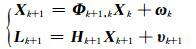
|
(13) |
式中,Φk+1, k为k+1时刻的状态转移矩阵,Φk+1, k=[0 0 E],E为单位阵,Xk为k时刻的n维状态向量,Xk=[dxT ΔdTmn ΔNi, mnp]kT,包含基线分量改正信息、接收机钟和模糊度参数,Lk+1为相位和码观测方程,Hk+1为设计矩阵,Hk+1=[A B Ck+1], Ck+1为k+1时刻的模糊度设计矩阵。假设ω和υ数学期望为0,彼此不相关,其协方差矩阵分别为Rk+1和Σk+1, k。自适应0-1选权滤波过程分为状态更新和测量更新, 状态更新过程如下[8]:
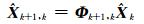
|
(14) |
采用自适应因子wi对观测方程测量更新,根据有无周跳将参数分为正常或者异常2类:

|
(15) |
将自适应0-1选权矩阵W作用于原参数矩阵,可以得到状态参数的等价权阵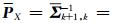
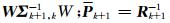
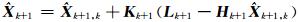
|
(16) |
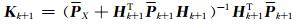
|
(17) |
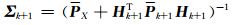
|
(18) |
滤波初值可以采用第1个历元或者前几个历元的站间单差模糊度浮点解及协方差阵。自适应选权滤波通过自适应因子调节状态参数的等价权阵,继而决定之前历元的状态信息是否参与当前历元的计算。
2.2 自适应选权因子选取自适应因子时,首先判断卫星是否发生升降,若前一历元某一卫星在当前历元消失,则自适应选权因子赋值为0,表示该历元不需要该卫星的先验信息;然后判断相位观测中是否发生周跳或者存在粗差,一般利用前后2个历元的新息向量之差进行判断,通过选定某个阈值可以确定是否发生异常(存在周跳或者粗差)[9]:
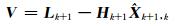
|
(19) |

|
(20) |
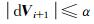
|
(21) |
或采用电离层残差组合和MW(Melbourne-Wbbena linear combination)的组合形式探测周跳和粗差,电离层残差组合和MW组合形式为:

|
(22) |
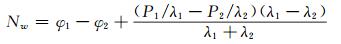
|
(23) |
选取观测时刻之前m个历元的观测数据进行开窗,可简单计算其均方根误差,其中〈〉为取整符号:
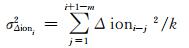
|
(24) |
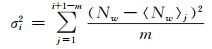
|
(25) |
当Δioni≥4σΔioni或|Nw-〈Nw〉i-1|≥4σi-1时,认为此时的相位观测值发生周跳或有粗差,对应的自适应因子赋值为0。
通过自适应选权滤波得到稳定的站间单差模糊度滤波解后,选基准卫星后得到稳定的双差模糊度浮点解及其协方差阵,此时的协方差阵包含更多的模糊度先验信息,理论上更能反映模糊度参数的真实情况。采用最小二乘降相关搜索算法固定双差模糊度,然后解算高精度的模糊度基线分量。本文采用第2种选权方案,该方案较为简单,理论严密,适合长时间高精度的静态和动态相对定位应用。该滤波方法实际上是一种0-1选权滤波模式,其好处是把周跳探测的过程和滤波的过程同时进行,较标准的卡尔曼滤波更加方便于应用。
3 算例分析分别采用实测静态和动态的实验数据验证新方案的性能,并设计3种解算方案进行对比分析。方案1:普通GPS双差单历元解;方案2:基于站间单差的GPS/GLONASS组合单历元解;方案3:基于自适应选权滤波的GPS/GLONASS算法。
实验一:采用2015-08-29武汉实测的2条长约2 m的短基线静态观测数据,分别用A1和B1表示,数据采样间隔设为1 s,共3 000个历元。采用GPS和GLONASS双系统双频观测数据进行测试,卫星截止高度角设为10°。
实验二:采用2014-07-31青岛实测的2条长约1 km的短基线静态实验数据,分别用A2和B2表示,数据采样间隔设为1 s, 共1 000个历元。采用GPS和GLONASS双系统的双频观测数据进行测试,卫星截止高度角设为10°。
实验三:采用2015-08-29武汉实测的动态短基线观测数据(对基线进行旋转),用A3表示,采样间隔为1 s,共13 000个历元。采用GPS和GLONASS双系统双频观测数据进行测试,卫星截止高度角设为10°。
实验四:采用2014-01-01澳大利亚科廷大学短基线IGS站(CUT0、CUTA)的静态实验数据,用A4表示,数据采样间隔设为30 s,共2 800个历元。采用GPS和GLONASS双系统双频观测数据进行测试,卫星截止高度角设为10°。采用1 d的观测数据检验算法在换星处理上的性能。
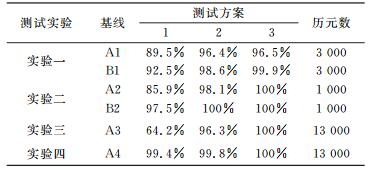
模糊度搜索结束后,一般将模糊度ratio值通过检验作为模糊度固定的重要判断标准。本文ratio取值为3。将整周模糊度固定成功率定义为模糊度固定成功的历元数与总历元数的比值,统计3种方案的模糊度固定成功率(表 2)。
|
|
表 2 3种方案模糊度解算成功率 Tab. 2 Success rate of ambiguity resolution using three schemes |
对比3种方案在4个实验中的模糊度固定成功率可知,不论静态实验或动态实验,方案2和方案3的成功率都高于仅采用GPS单系统的方案1。特别是在动态情况下(实验三),较长的一段时间过程中,单系统卫星数较少,测距码和相位的噪声都比较大,单一的GPS系统解算模糊度的成功率只有64.2%;添加GLONASS系统后,卫星数增加,更多的观测信息引入,模糊度解算成功率则超过95%,体现了多系统固定模糊度的优点。与方案2相比,采用自适应选权滤波的方案3进一步提高了模糊度固定的成功率,在实验二、三、四中,模糊度固定成功率都达到100%,说明该算法更好地利用了之前历元的站间单差模糊度信息,提高了双差模糊度固定的成功率。
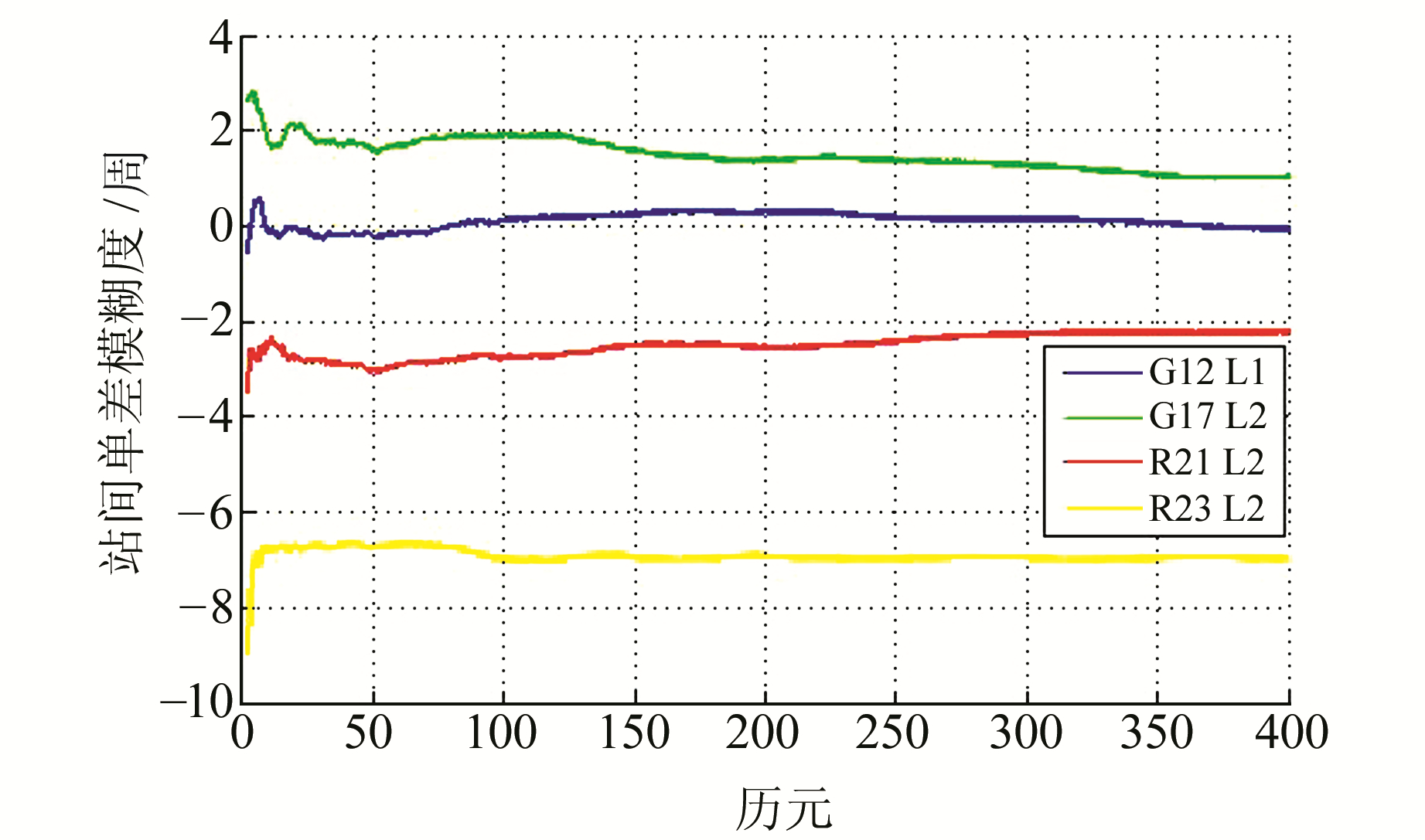
为分析站间单差模糊度滤波后的收敛情况,分别统计2颗GPS卫星和2颗GLONASS卫星的基频站间单差模糊度滤波结果(图 1)。由图 1可知,站间单差模糊度在20个历元以内基本可以收敛,并长时间保持稳定的状态,为整个算法的实现提供了正确的依据。
|
图 1 G12、G17、R21、R23卫星模糊度站间单差滤波解 Fig. 1 The result of the single difference between stations of ambiguity |
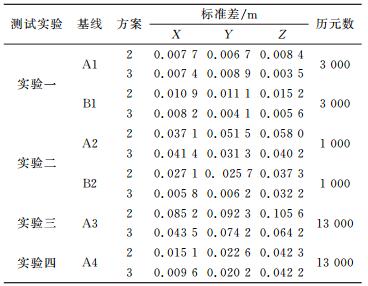
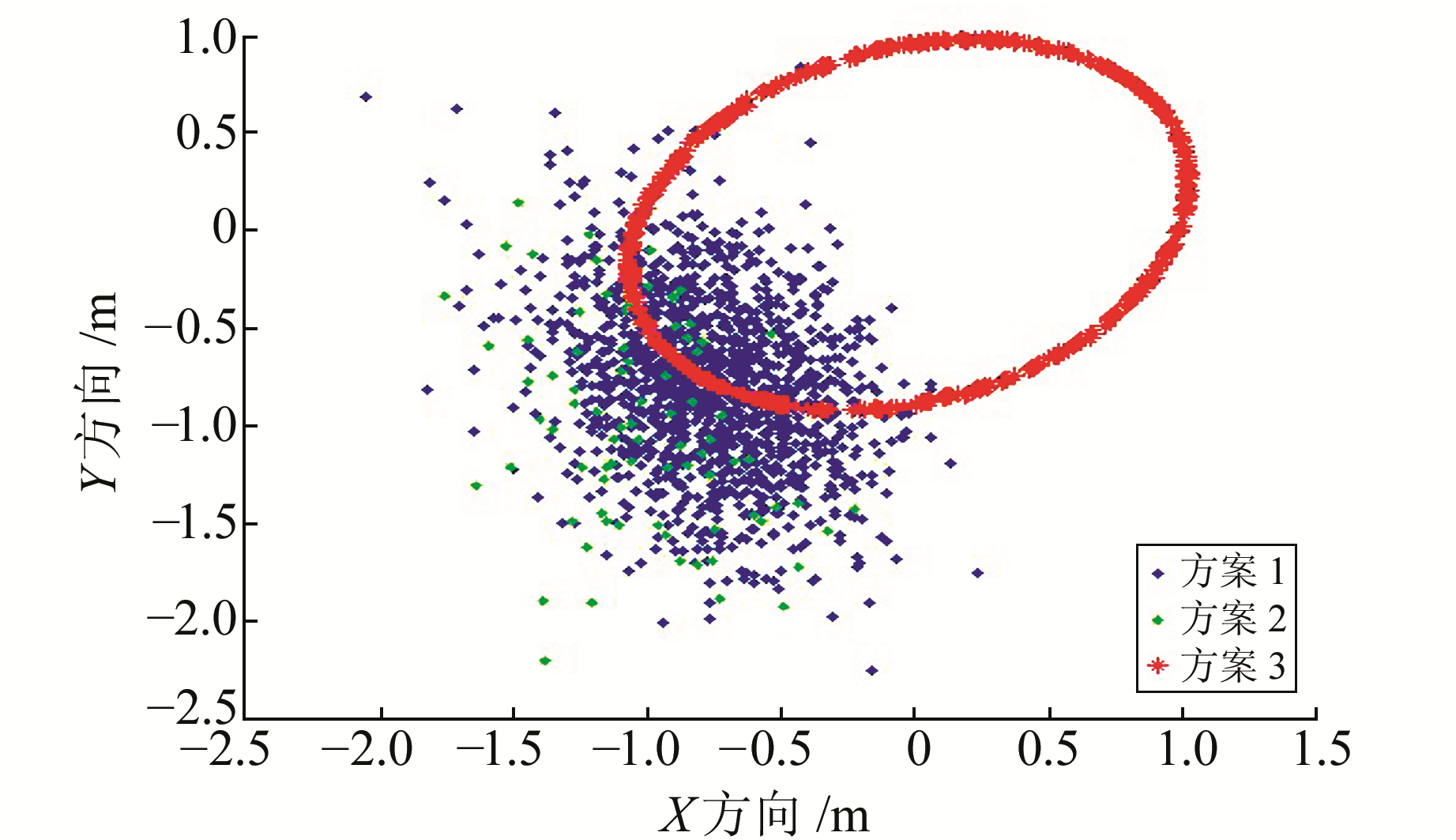
为进一步验证新算法,统计实验二和实验三基线解算结果,图 2、3分别为方案1、2和3在静态和动态实验中最后解算的水平基线分量。

|
图 2 静态基线水平分量结果比较 Fig. 2 The accuracy comparison of static baseline solution |
|
图 3 动态基线水平分量结果比较 Fig. 3 The accuracy comparison of dynamic baseline solution |
从表 2和图 2可以看出,静态相对定位实验中(实验一、二、四),采用GPS+GLONASS双系统的解算效果明显优于GPS单系统的定位效果,主要原因是GPS在相当多的历元里观测卫星少于5颗,此时由模糊度精度因子ADOP (ambiguity dilution of precision)算出的先验模糊度成功率很低,模糊度固定困难。对比方案1和2,方案3通过自适应选权滤波将之前历元的站间单差模糊度浮点解作为虚拟观测值,代入当前历元的观测方程中,有效改善了站间单差模糊度模型误差大、观测信息不足以及观测数据质量较差的问题,进而提高了基线解的精度。分析表 2和图 3可得,动态情况下方案3的精度仍优于方案1和2,因为站间单差模糊度并不随参考站或移动站位置改变而变化,之前历元的选权滤波的信息仍然可用,进而提高了站间单差模糊度浮点解及协方差阵的精度。
|
|
表 2 方案2和方案3算法的解算精度 Tab. 2 Calculation accuracy of method 2 and method 3 |
在静态和动态实验中,当GPS卫星观测数较少、观测条件较差时,仅采用单卫星系统有时很难正确固定双差模糊度,只能用实数解代替。而GPS/GLONASS双系统可以明显增加可见卫星数目,增加多余观测,提高基线解算的精度。采用站间单差的自适应选权滤波方案直接利用原始单差观测值进行滤波处理,仅需简单的周跳探测过程,无需进行复杂的换星操作,较传统的滤波手段更加简便易行。
4 结语本文设计了基于站间单差的自适应选权滤波方案,该方案考虑GLONASS系统的特殊性,不需要进行复杂的换星操作,直接利用原始单差观测值进行滤波处理。由于新算法合理利用站间单差模糊度的时不变性,有效地提高了模糊度浮点解的精度并缩小了模糊度搜索椭球的空间,进而提高了双差模糊度固定的成功率和相对定位的精度。
致谢: 本文部分实验数据由中国科学院测量与地球物理研究所王海涛副研究员提供,特此感谢!
| [1] |
Wanninger L. Carrier-Phase Inter-Frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 1-10
(  0) 0) |
| [2] |
张宝成, 袁运斌, 蒋振伟. 一种无须变换参考星的GNSS单基线卡尔曼滤波算法[J]. 测绘学报, 2015, 44(9): 958-964 (Zhang Baocheng, Yuan Yunbin, Jiang Zhenwei. Kalman Filter-Based Single-Baseline GNSS Data Processing without Pivot Satellite Changing[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 958-964)
(  0) 0) |
| [3] |
张宝成, 欧吉坤, 袁运斌. 基于精选基准消秩亏的GNSS参考网数据处理方法[J]. 测绘学报, 2014, 43(9): 895-901 (Zhang Baocheng, Ou Jikun, Yuan Yunbin. Method of Processing GNSS Reference Network Data with Refined Datum Definition for Rank-Deficiency Elimination[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 895-901)
(  0) 0) |
| [4] |
陈源军, 易重海, 匡翠林, 等. 基于虚拟观测值后验方差估计的整周模糊度快速固定方法[J]. 大地测量与地球动力学, 2016, 36(2): 158-161 (Chen Yuanjun, Yi Zhonghai, Kuang Cuilin, et al. Fast GPS Ambiguity Resolution with Variance Component Estimation Based on Virtual Observation[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 158-161)
(  0) 0) |
| [5] |
Nie Z X, Gao Y, Wang Z J, et al. Performance Analysis of Combined GPS, GLONASS and Beidou RTK Based on Single Differenced Observations between Receivers[C].The 28th International Technical Meeting of the Satellite Division of the Institute of Navigation, Florida, 2015
(  0) 0) |
| [6] |
欧吉坤, 柴艳菊, 袁运斌.自适应选权滤波[A]//大地测量与地球动力学进展[M].武汉: 湖北科学技术出版社, 2004 (Ou Jikun, Chai Yanju, Yuan Yunbin. Adaptive Filtering by Selecting the Parameter Weight Factor [A]//Progress in Geodesy and Geodynamics[M]. Wuhan: Hubei Science and Technology Press, 2004)
(  0) 0) |
| [7] |
甘雨, 隋立芬, 刘长建, 等. 自适应抗差Kalman滤波在多天线原始观测值瞬时姿态确定中的应用[J]. 测绘学报, 2015, 44(9): 945-951 (Gan Yu, Sui Lifen, Liu Changjian, et al. Instantaneous Attitude Determination Based on Original Multi-Antenna Observations Using Adaptively Robust Kalman Filtering[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 945-951)
(  0) 0) |
| [8] |
李增科, 王坚, 高井祥, 等. 自适应联邦滤波器在GPS-INS-Odometer组合导航的应用[J]. 测绘学报, 2016, 45(2): 157-163 (Li Zengke, Wang Jian, Gao Jingxiang, et al. The Application of Adaptive Federated Filter in GPS-INS-Odometer Integrated Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 157-163)
(  0) 0) |
| [9] |
Ren C, Ou J K, Yuan Y B. Application of Adaptive Filtering by Selecting the Parameter Weight Factor in Precise Kinematic GPS Positioning[J]. Progress in Natural Science, 2005, 15(1): 41-46 DOI:10.1080/10020070512331341750
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, 340 Xudong Street, Wuhan 430077, China
 2017, Vol. 37
2017, Vol. 37