2. 国家测绘地理信息局第三大地测量队,成都市公园路一段62号,610100
传统相对定位一般采用双差观测值作为基本观测量,通过观测值之间的相关性建立随机模型[1]来估计坐标参数,但多个测站观测值之间的相关性很难通过误差传播定律来表示,这是目前大多数商业软件依然采用单基线解算的重要原因,也是影响多个测站数据联合解算的关键问题之一。
众所周知,无论是采用非差观测值还是双差观测值,其算法是等价的,两者并没有本质的区别[2]。非差观测值具有相互独立的优点,避免了双差观测值的复杂相关性,有利于多个测站数据的联合处理。近年来,等价单差和等价双差观测方程[3]的推导以及简化等价观测方程理论[4-5]的提出,为非差观测值进行多基线解算提供了理论基础。文献[4]针对伪距观测值进行了实例计算,文献[5]对比了简化等价方法与传统方法的计算效率。但仍然缺少有关相位观测值进行多基线解算,尤其是多基线模糊度解算方面的研究。另外,部分模糊度固定(PAR)方法[6-10]已经成功应用于单基线模糊度的解算之中,而多基线模糊度的个数成倍增加,相同基线和不同基线之间的模糊度相关性更为复杂,如何快速准确地固定多基线模糊度是实现多基线解算的关键问题,有必要对此进行深入探讨。本文在上述研究成果的基础上,首先采用非差观测值构建多个测站的等价观测方程,并针对多基线模糊度的特点实现一种部分模糊度的快速固定方法,最后通过实例数据对上述方法的有效性和可靠性进行验证。
1 多基线解算模型假设网中共有k个测站,共观测到n颗卫星,短基线情况下忽略对流层误差、电离层误差和多路径误差等影响,k个测站的非差观测方程线性化的矩阵形式可表示为:
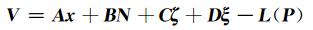
|
(1) |
式中,x为k-1个流动站的坐标参数;N为所有非差模糊度参数;ζ为k-1个接收机钟差参数;ξ为n颗卫星钟差参数;P为非差观测值权阵,可采用高度角来定权。为便于操作,以卫星的顺序进行排序,则各系数矩阵和常数项表达如下:

|
式中,下标k、j(j=1, …, n)为各卫星对应的测站观测数,I表示元素为1的向量,E表示单位矩阵。
根据等价变换原理,可构造消卫星钟差参数的变换矩阵:
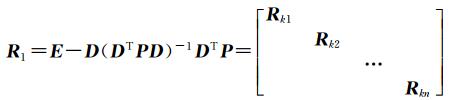
|
(2) |
式中,R1的秩亏数为n,这是由原始非差模糊度转变为测站间等价单差模糊度所引起的模糊度秩亏。为使参数独立化,需固定各卫星对应的基准站非差模糊度参数,还需固定基准站的钟差参数,其余流动站钟差参数转变为相对钟差参数。
在式(1)两边左乘变换矩阵R1, 得到等价单差观测方程:
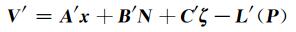
|
(3) |
式中,V′=R1V,A′=R1A,B′=R1B,C′=R1C,L′=R1L,权阵P保持不变。
再次构造消接收机钟差参数的变换矩阵:

|
(4) |
式中,R2的秩亏数为k-1,这是由测站间等价非差模糊度转变为站星等价双差模糊度引起的秩亏。为保持参数的独立性,需固定非基准站对应的基准卫星非差模糊度参数。
在式(3)两边左乘变换矩阵R2,得到等价双差观测方程:
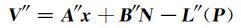
|
(5) |
式中,V″=R2V′,A″=R2A′,B″=R2B′,C″=R2C′,L″=R2L′,权阵P保持不变。至此,式(5)已完全消除了钟差参数,模糊度N即为等价双差模糊度。该方程在保证各非差观测值独立的前提下,统一了非差、单差、双差数据处理方法,实现了多测站数据的联合解算。另外,等价方程也可以通过简化方法来构建[5]。
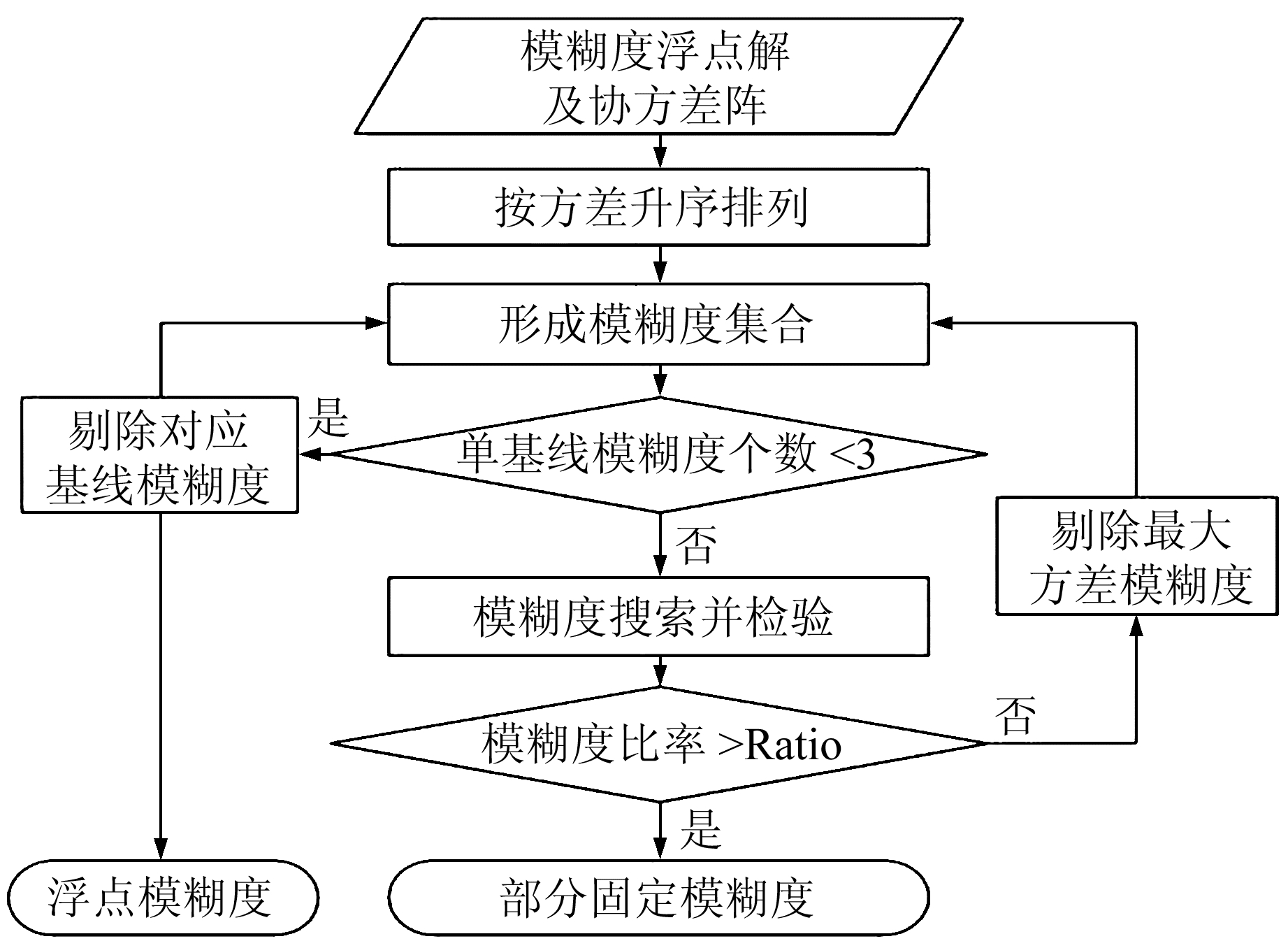
2 部分模糊度固定方法在多基线解算中,等价模糊度个数是各单基线模糊度个数之和。若k个测站同时观测n颗卫星,采用L1相位观测值构建等价方程,坐标参数为3×(k-1)个,模糊度参数为(n-1)×(k-1)维,且相同基线模糊度、不同基线模糊度之间均具有较强的相关性。如果某一个模糊度无法固定,必将导致整个历元解算失败,因此采用PAR方法进行多基线解算尤为重要。本文首先通过消坐标参数的卡尔曼滤波估计[11]获得模糊度浮点解及其协方差矩阵,再进行模糊度搜索,最后回代模糊度固定值求解坐标参数。图 1给出了部分模糊度固定的流程图。
|
图 1 部分模糊度固定流程 Fig. 1 Flowchart of partial ambiguity fixing |
由图 1知,经过升序排列后的所有模糊度形成集合,采用LAMBDA方法[12]进行搜索,当比率值大于设定阀值(Ratio=2)时,得到模糊度固定值。如果不满足阀值要求,则循环剔除最大方差模糊度,直至通过Ratio检验或者模糊度个数小于3为止。特别说明的是,多基线解算中某一基线模糊度个数小于3时,该基线模糊度采用浮点值,不再继续循环检验。当完成部分模糊度固定后,需要利用已固定的模糊度继续解算其他未固定的模糊度,避免某一基线模糊度解算不成功的问题,直到没有更多的模糊度固定为止。
3 实例计算与分析本文采用5个IGS观测站的实测数据分析以上方法的可靠性。数据观测时间为2011-04-10(年积日100)00:00~24:00(GPST),采样间隔15 s,卫星截止高度角15°,该段数据最多可观测卫星12颗,最少7颗。选取P216基准站,其余测站与其构成短基线,其中最短约6.1 km,最长约13.9 km(图 2)。

|
图 2 测站分布 Fig. 2 Distribution of stations |
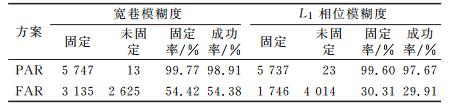
首先对多基线宽巷模糊度进行估计,进而利用已固定的宽巷模糊度加速求解L1相位模糊度,并分别采用PAR方法和FAR方法进行模糊度搜索。表 1给出了两种方法的模糊度固定率和成功率。其中,固定率=固定历元数/总历元数,成功率=正确固定历元数/总历元数。在相同宽巷模糊度精度的情况下,FAR方法模糊度固定率为54.42%,低于PAR方法的99.77%;随着L1相位模糊度估计精度差异的逐渐增大,FAR方法固定率为30.31%,远低于PAR方法的99.60%。另外,模糊度的成功率与固定率具有较好的一致性,PAR方法模糊度成功率高于FAR方法。在宽巷模糊度固定的情况下,PAR方法较FAR方法具有更高的L1相位模糊度固定水平。
|
|
表 1 模糊度固定率和成功率的对比 Tab. 1 AR performance comparison |
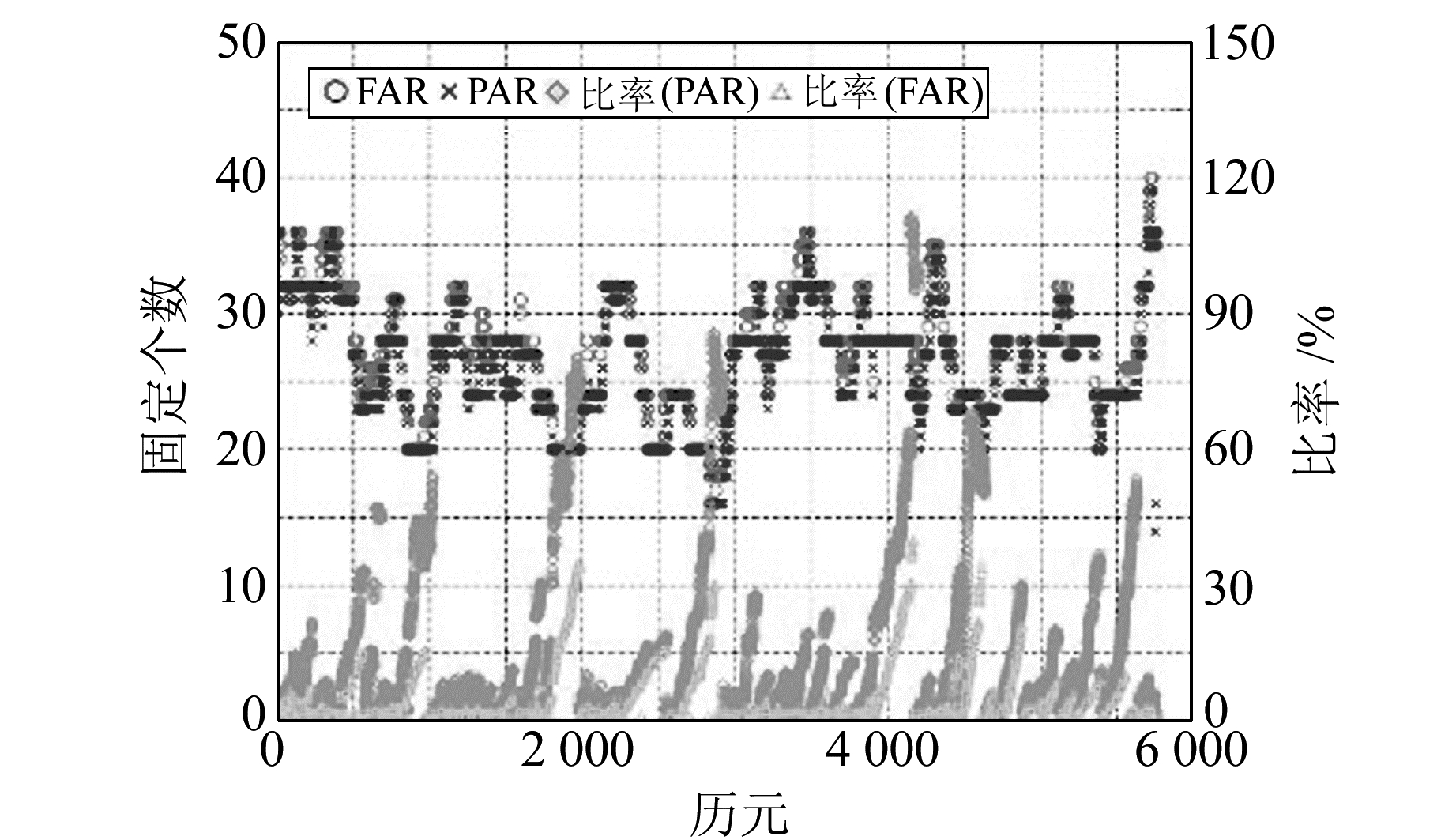
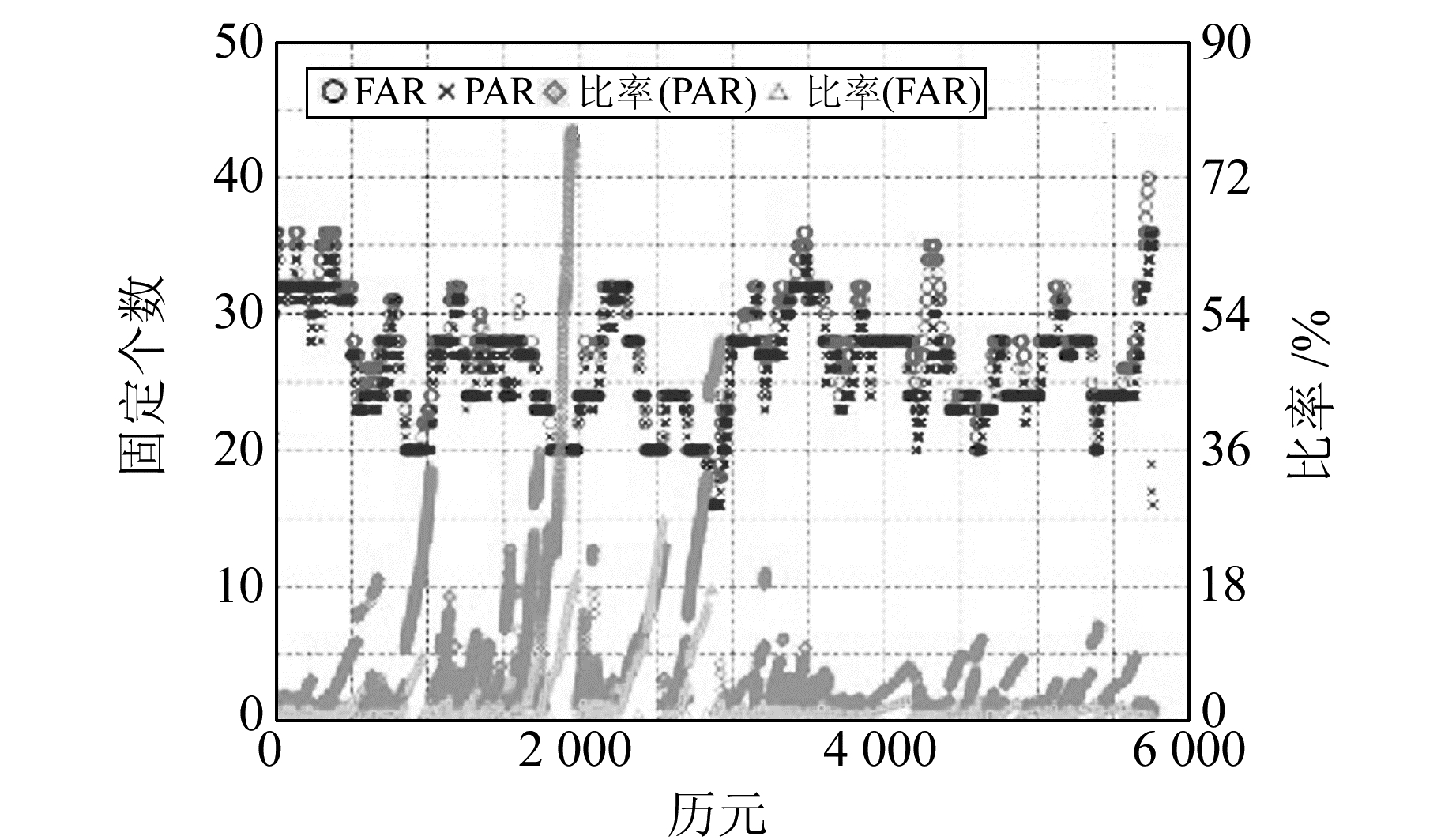
图 3和4分别给出了两种方法固定模糊度的个数以及模糊度固定比率。分析可知,大部分历元的模糊度个数处于20~32之间,最大个数约为40。模糊度个数越多,模糊度固定比率越小;模糊度个数越少,模糊度固定比率越大。PAR方法的模糊度固定比率普遍大于FAR方法,可见在多基线模糊度解算中,PAR方法具有更高的效率。
|
图 3 宽巷模糊度固定个数和比率 Fig. 3 Imformation of the wide-lane AR |
|
图 4 L1相位模糊度固定个数和比率 Fig. 4 Imformation of the L1 AR |
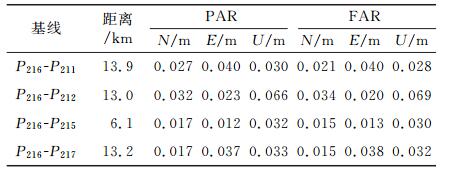
模糊度固定后,回代方程求解坐标参数。分别将PAR方法和FAR方法解算的三维基线分量与IGS站精确坐标反算的基线分量进行对比,统计各方向上基线分量的均方根误差见表 2,误差时间序列见图 5和6。
|
|
表 2 各基线分量均方根误差 Tab. 2 RMS of the L1 carrier phase multi-baseline resolution |
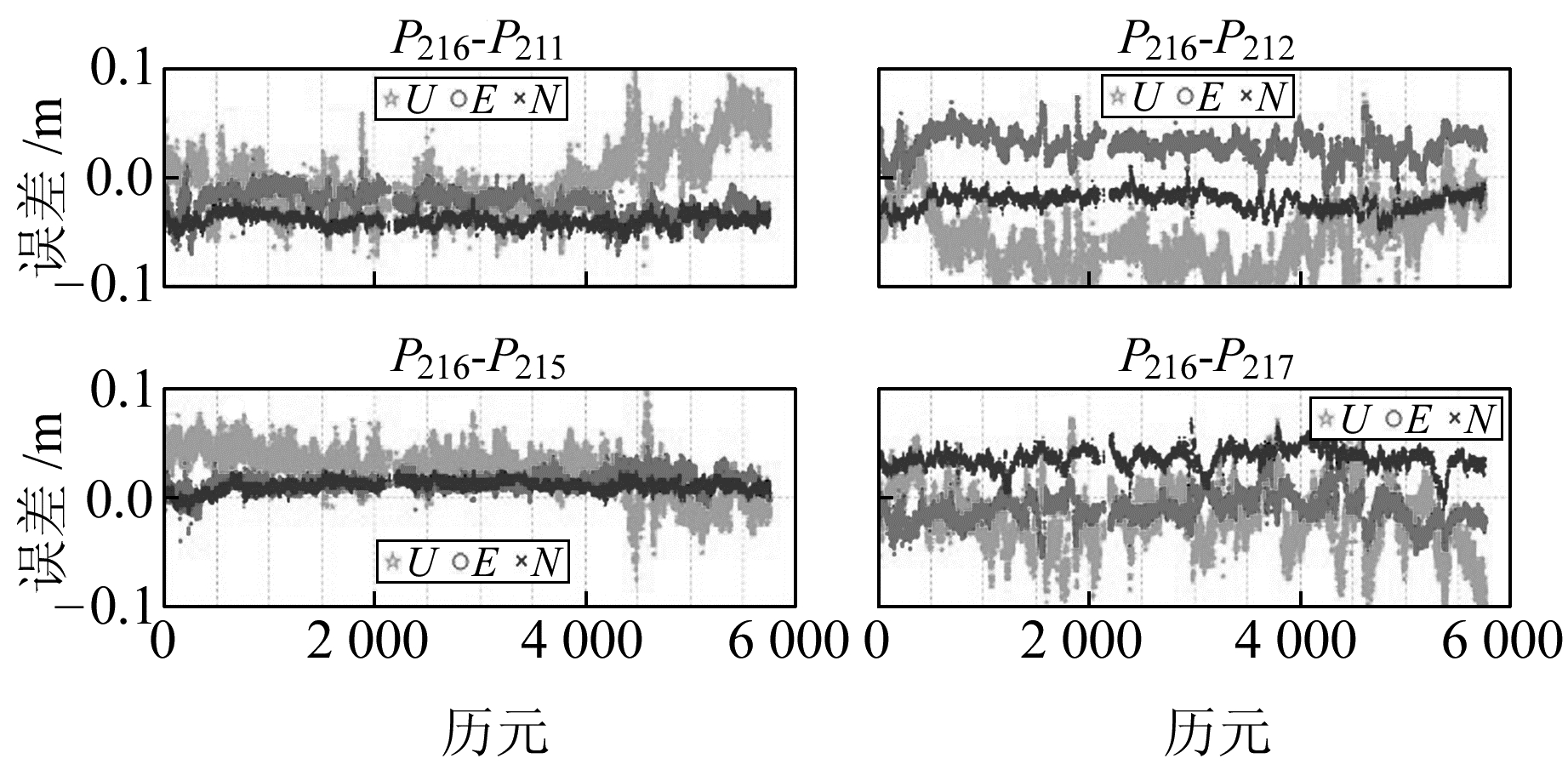
|
图 5 各基线分量误差序列(PAR方法) Fig. 5 Error of the L1 carrier phase multi-baseline resolution with PAR method |
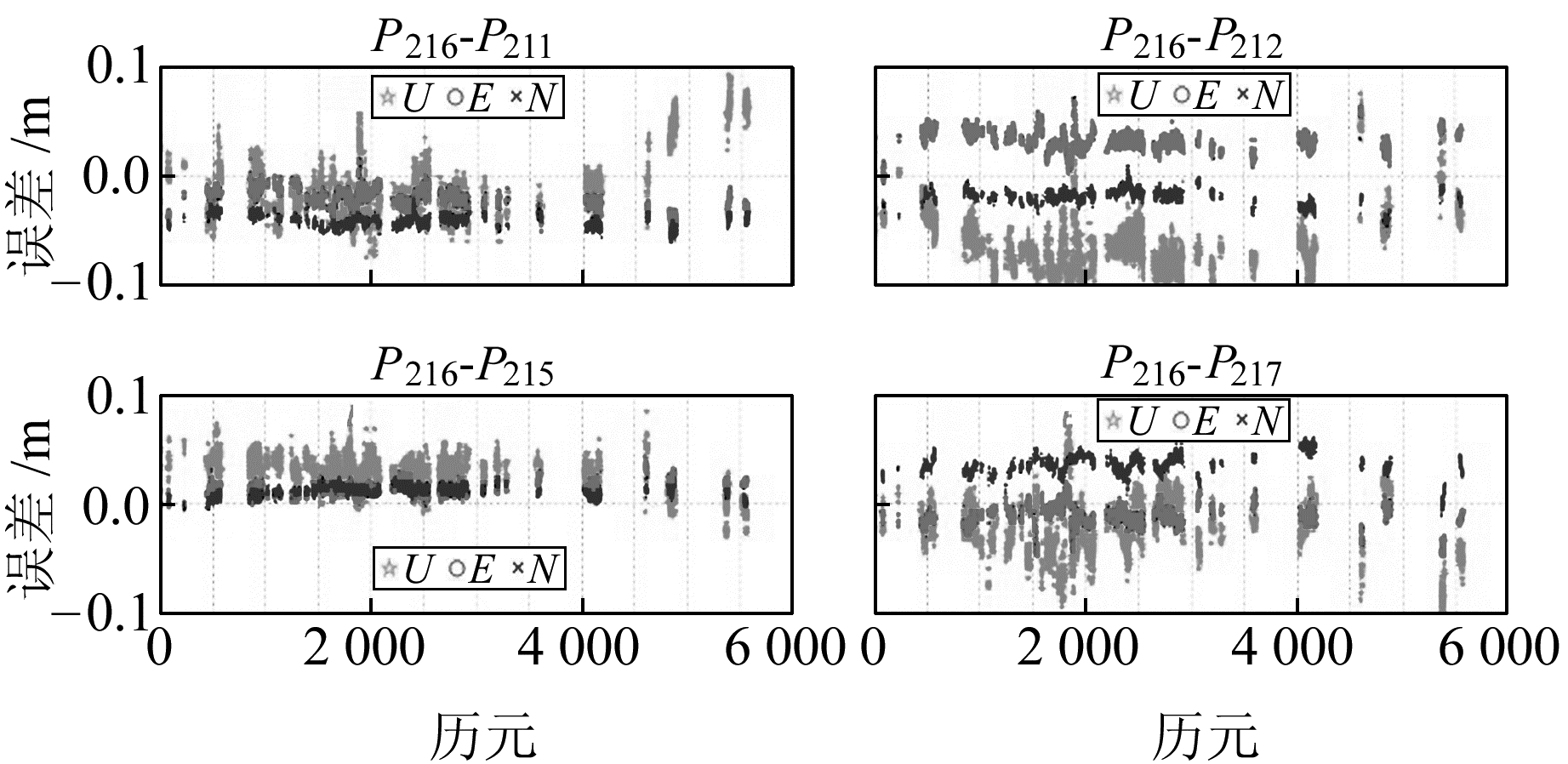
|
图 6 各基线分量误差序列(FAR方法) Fig. 6 Error of the L1 carrier phase multi-baseline resolution with FAR method |
分析表 2可知,各基线水平位置分量精度优于5 cm,高程分量优于7 cm。PAR方法与FAR方法分量误差无显著差异,这是因为PAR方法在确保通过Ratio检验的前提下,最大限度地保留了模糊度个数及观测值信息,两者平差系统无显著差异,精度趋于一致。另外,距离较短的基线P216-P215其解算精度相对较高。
对比图 5和6,在FAR方法无法成功解算的时间段,PAR方法都能获得较好的基线分量信息。究其原因,多基线模糊度个数较多,极少数模糊度观测误差较大,无法获得模糊度固定值,而PAR方法恰好剔除了该部分模糊度,有效固定了其他模糊度,获得了较好的解算结果。
4 结语多基线解算方法采用非差观测值构建误差方程,通过等价变换消除钟差参数,形成等价双差观测方程。该方法实现了从非差观测值到双差观测值数据处理方法的转换,避免了双差观测值的构建及相关问题,有利于多个测站数据的联合解算。
PAR方法通过不断循环剔除最大方差模糊度并进行Ratio检验,实现了部分模糊度的固定,不仅显著提高了多基线模糊度的固定率和成功率,提高了多基线精密定位的可用性,且PAR坐标精度与FAR具有较好一致性,为多基线解算方法的应用提供了可靠条件。
致谢: 感谢IGS分析中心提供实验数据。
| [1] |
刘大杰, 施一民, 过静珺. 全球定位系统(GPS)的原理与数据处理[M]. 上海: 同济大学出版社, 1999 (Liu Dajie, Shi Yimin, Guo Jingjun. The Principle and Data Processing of Global Positioning System[M]. Shanghai: Tongji University Press, 1999)
(  0) 0) |
| [2] |
魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1997 (Wei Ziqing, Ge Maorong. Relative Positioning Mathematics Model in Global Positioning System[M]. Beijing: Surveying and Mapping Press, 1997)
(  0) 0) |
| [3] |
Xu G C. GPS Data Processing with Equivalent Observation Equations[J]. GPS Solutions, 2002(6): 28-33
(  0) 0) |
| [4] |
Shen Y Z, Xu G C. Simplified Equivalent Representation of GPS Observation Equations[J]. GPS Solutions, 2008(2): 99-108
(  0) 0) |
| [5] |
李博峰.混合整数GNSS函数模型及随机模型参数估计理论与方法[D].上海: 同济大学, 2010 (Li Bofeng. Theory and Method of Parameter Estimation for Mixed Integer GNSS Stochastic and Function Models[D]. Shanghai: Tongji University, 2010) http://www.cqvip.com/QK/90069X/201003/34401608.html
(  0) 0) |
| [6] |
Li P, Zhang X H. Precise Point Positioning with Partial Ambiguity Fixing[J]. Sensors, 2015, 15: 13627-13643 DOI:10.3390/s150613627
(  0) 0) |
| [7] |
Li B F, Shen Y Z, Feng Y M, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99-112 DOI:10.1007/s00190-013-0670-z
(  0) 0) |
| [8] |
Verhagen S, Teunissen P J G, Marel H, et al. GNSS Ambiguity Resolution: Which Subset to Fix? [C].IGNSS Symposium 2011, Sydney, 2011
(  0) 0) |
| [9] |
潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210-1218 (Pan Zongpeng, Chai Hongzhou, Liu Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-Difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210-1218 DOI:10.11947/j.AGCS.2015.20150056)
(  0) 0) |
| [10] |
赵兴旺.基于相位偏差改正的PPP单差模糊度快速解算问题研究[D].南京: 东南大学, 2011 (Zhao Xingwang. Precise Point Positioning with Single Difference Ambiguity Resolution Based on Phase Biases Correction[D]. Nanjing: Southeast University, 2011) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2054341
(  0) 0) |
| [11] |
刘宁, 熊永良, 冯威, 等. 单频GPS动态定位中整周模糊度的一种快速解算方法[J]. 测绘学报, 2013, 42(2): 211-217 (Liu Ning, Xiong Yongliang, Feng Wei, et al. An Algorithm for Rapid Integer Ambiguity Resolution in Single Frequency GPS Kinematical Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 211-217)
(  0) 0) |
| [12] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70: 65-82 DOI:10.1007/BF00863419
(  0) 0) |
2. Geodetic Third Team, NASMG, 62 First Segment of Gongyuan Road, Chengdu 610100, China
 2017, Vol. 37
2017, Vol. 37