如何有效分离GPS时间序列中包含的各类噪声已成为目前研究的热点。王敏等[1]、张飞鹏等[2]、姜卫平等[3]、袁林果等[4]研究了我国境内IGS站及区域CORS站的GPS时间序列的运动特性,结果表明GPS时间序列在水平方向主要以线性运动为主,而高程方向则表现出复杂的周期振荡与非线性运动,且不同测站的周期振荡特性并不相同。张恒璟等[5]用经验模态分解(empirical mode decomposition, EMD)方法分析GPS垂向时间序列的振荡周期,结果表明GPS垂向时间序列并非严格地以固定的年周期或半年周期运动,且趋势项多以非线性为主,因此用谐波模型求解参数拟合GPS时间序列可能偏离甚至违背原序列的运动特性,进而导致用于噪声分析的残差序列不可避免地包含某种误差或错误。贾瑞生等[6]研究了EMD方法在微震信号降噪中的应用,罗飞雪等[7]提出EMD-ICA法、交叉认证的EMD方法进一步提取信号与噪声混合的IMF分量中的信号。本文用EMD方法对GPS位置时间序列作降噪分析,并验证该方法的有效性。
1 EMD用于GPS位置时间序列降噪的基本原理 1.1 EMD分解GPS时间序列的基本原理EMD的基本思想是把随机过程x(t)分解成m个不同时间尺度的IMF和一个趋势项Tk。每个IMF必须满足以下2个条件:在整个序列中,极值点的数目与过零点的数目必须相等或最多相差1个;由局部极大值所构成的包络线以及由局部极小值所构成的包络线的平均值为0[6-7]。因此随机过程x(t)可表示为:
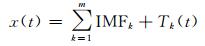
|
(1) |
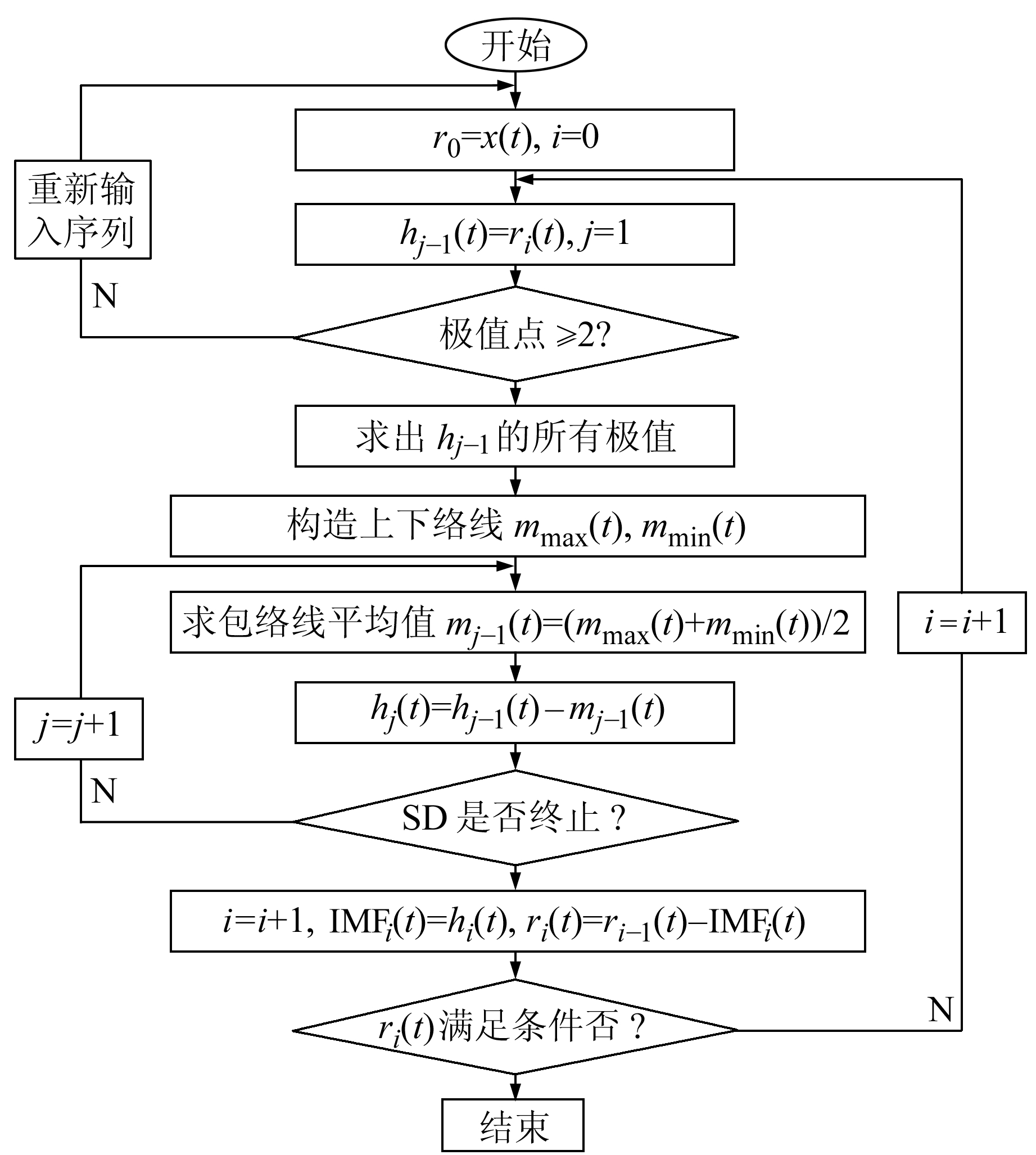
式中,Tk(t)为序列的趋势项;IMF为本征模态分量,反映信号自身固有的、内在的特征。EMD的具体分解过程如图 1所示。
|
图 1 EMD分解流程 Fig. 1 Flow chart of EMD decompose |
图 1中,x(t)为待分解序列;hi(t)为第i个IMF;ri(t)为分解过程中序列的余项,当其满足单调条件时序列分解结束,此时ri(t)为所分解序列的趋势项Tk(t);SD为各IMF的筛选准则,其表达式为:
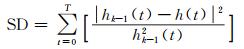
|
(2) |
式中,hk-1(t)与h(t)为相邻的2个IMF;SD为停止筛选过程的判断依据,实际应用中SD可取0.2~0.3。
1.2 分解序列重构为了获取“干净”的GPS位置时间序列,需要分离出序列中的噪声,因此需确定m个IMF信号与噪声的分界本征模态分量IMFk[6]。首先,求取m个IMF与原序列的相关系数。其次,搜索求得的一系列相关系数中第一个取局部极小值的相关系数对应的本征模态分量IMFk为噪声与信号的分界IMF。因我国境内IGS连续跟踪站的最佳噪声模型为WN+FN,但不同测站噪声特性略有差异[8],因此将分界IMFk归入到噪声层。最后,将k及k之前的IMF重构为噪声序列,将k之后的IMF重构为降噪序列。通过重构被分解序列获得原序列中的周期项、趋势项及噪声序列。
2 算例实验分析选取我国境内及周边9个IGS站时间序列进行降噪分析。GPS位置时间序列来源于IGS数据分析中心SOPAC提供的GPS台站位置单日解序列,其中最长序列为上海(SHAO,20.38 a)站,最短序列为长春(CHAN,10.46 a)站。受地质灾害、人为因素等的影响,GPS站位置时间序列难免会出现跃阶现象,如长春站受东日本大地震的影响在N、E、U方向分别有-9.46 mm、21.73 mm、-1.56 mm的跃阶,WUHN站U方向在2002.07历元处因换天线基座有38.59 mm的跃阶。在进行序列分析前需对序列中出现的跃阶项进行修正并剔除序列中个别粗差点。
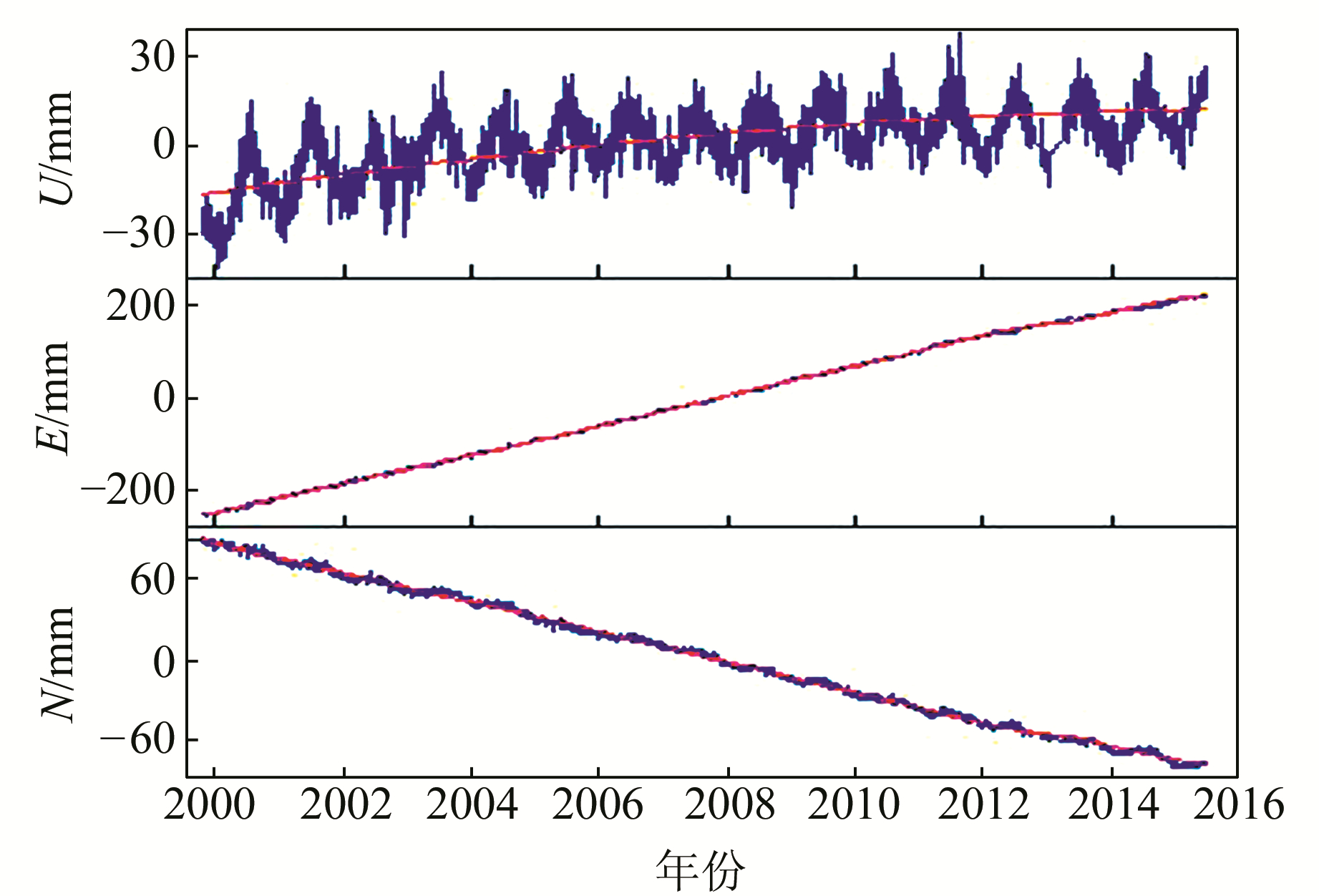
2.1 算例分析用上述方法对9个IGS站的N、E、U方向分别作降噪分析,限于篇幅,仅以北京房山(BJFS, 15.69 a)站为例说明该方法的有效性及可行性(图 2,蓝色和红色线条分别为原始序列和趋势项)。
|
图 2 北京房山站时间序列 Fig. 2 Time series of BJFS station |
由图 2可知,U方向具有明显的周期性,且存在一个非线性的趋势项,而N、E方向则以明显的线性运动为主。各方向趋势项与原序列的相关系数见表 1。
|
|
表 1 BJFS站原序列与趋势项相关系数 Tab. 1 Original and trend series′s correlation coefficient of BJFS station |
由表 1可知,EMD方法能很好地获得各方向的趋势项,尤其在N、E方向上。用EMD方法获取其他8个站N、E、U方向的趋势项并计算其相关系数。结果表明,N、E方向上所有站点的相关系数均在0.99以上,且趋势项主要呈线性分布;而U方向上的相关系数明显小于N、E方向,这主要是因为U方向起伏较大的周期项所致。
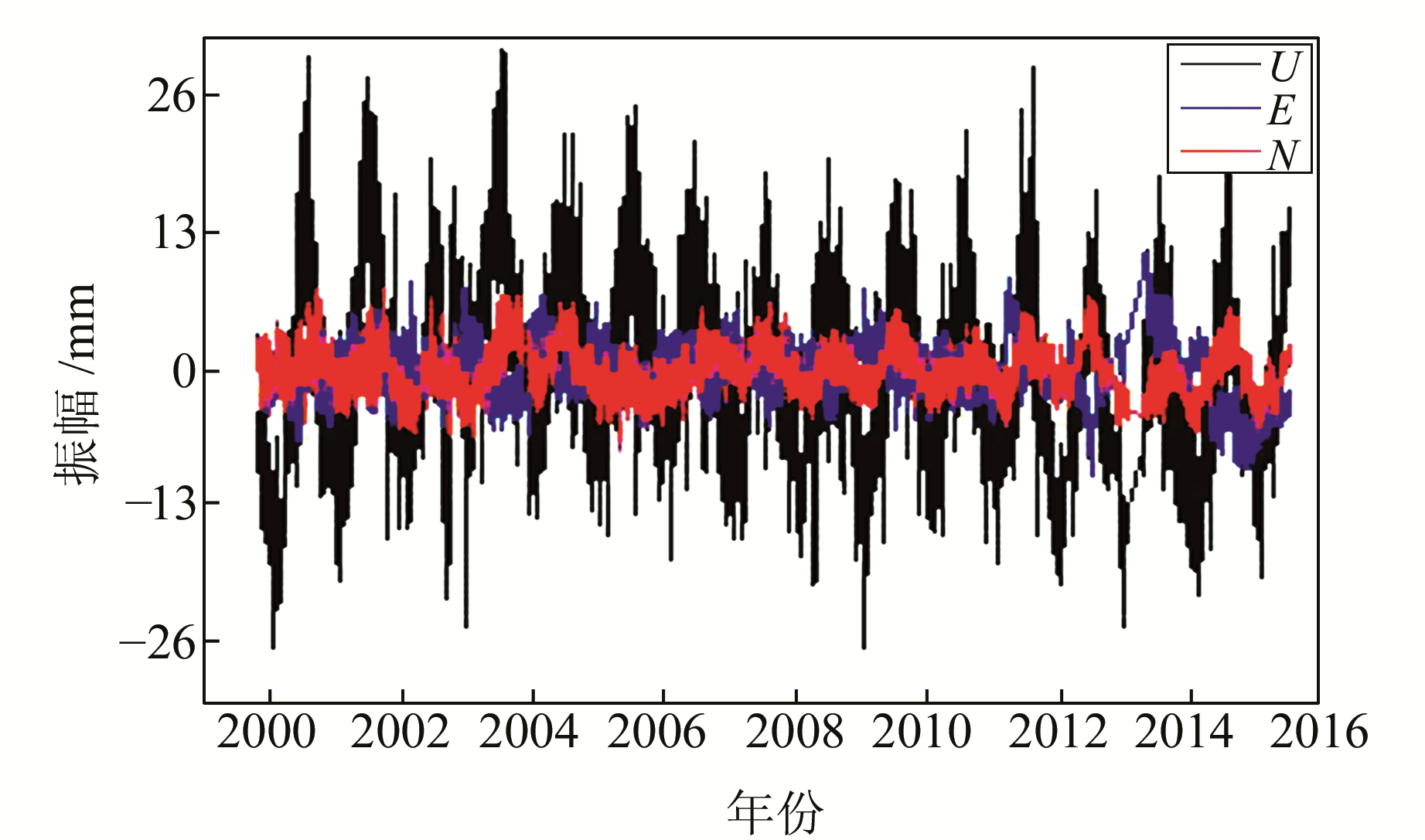
图 3为BJFS站各方向去趋势项后的序列。可以看出,去趋势项后N、E、U方向均表现出明显的周期性变化,U方向的周期变化较N、E方向更剧烈。为了进一步分析各方向的周期性变化,用相同的方法获取其他8个IGS站去趋势项后的序列,得到了与图 3相同的效果。这说明周期性不仅仅体现在高程方向,在水平方向上也有体现,但由于水平方向主要以线性运动为主,且其运动速率较大,在视觉上常常掩盖了相对较弱的周期性变化。
|
图 3 BJFS站去趋势项序列 Fig. 3 Diminuer trend series of BJFS station |
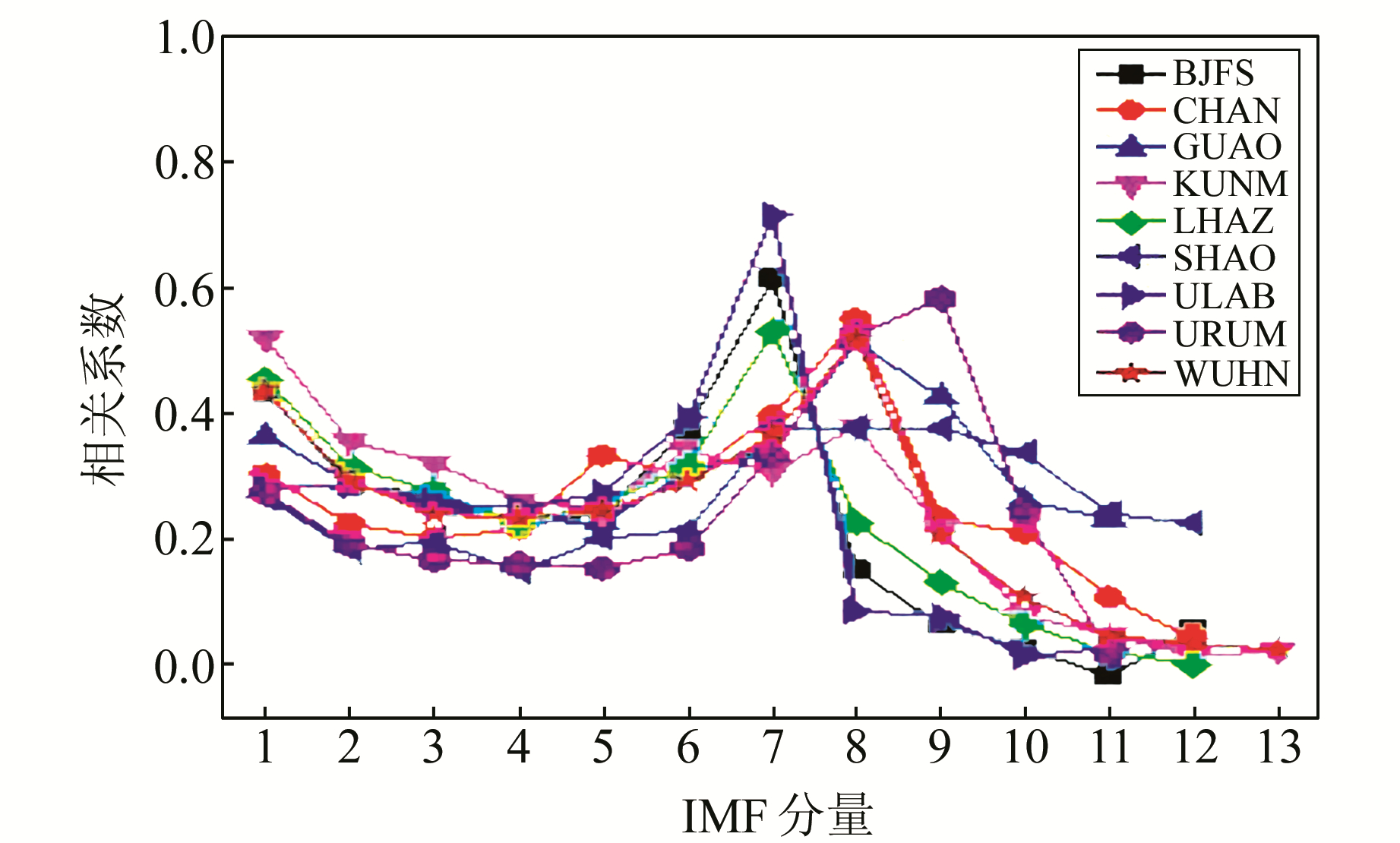
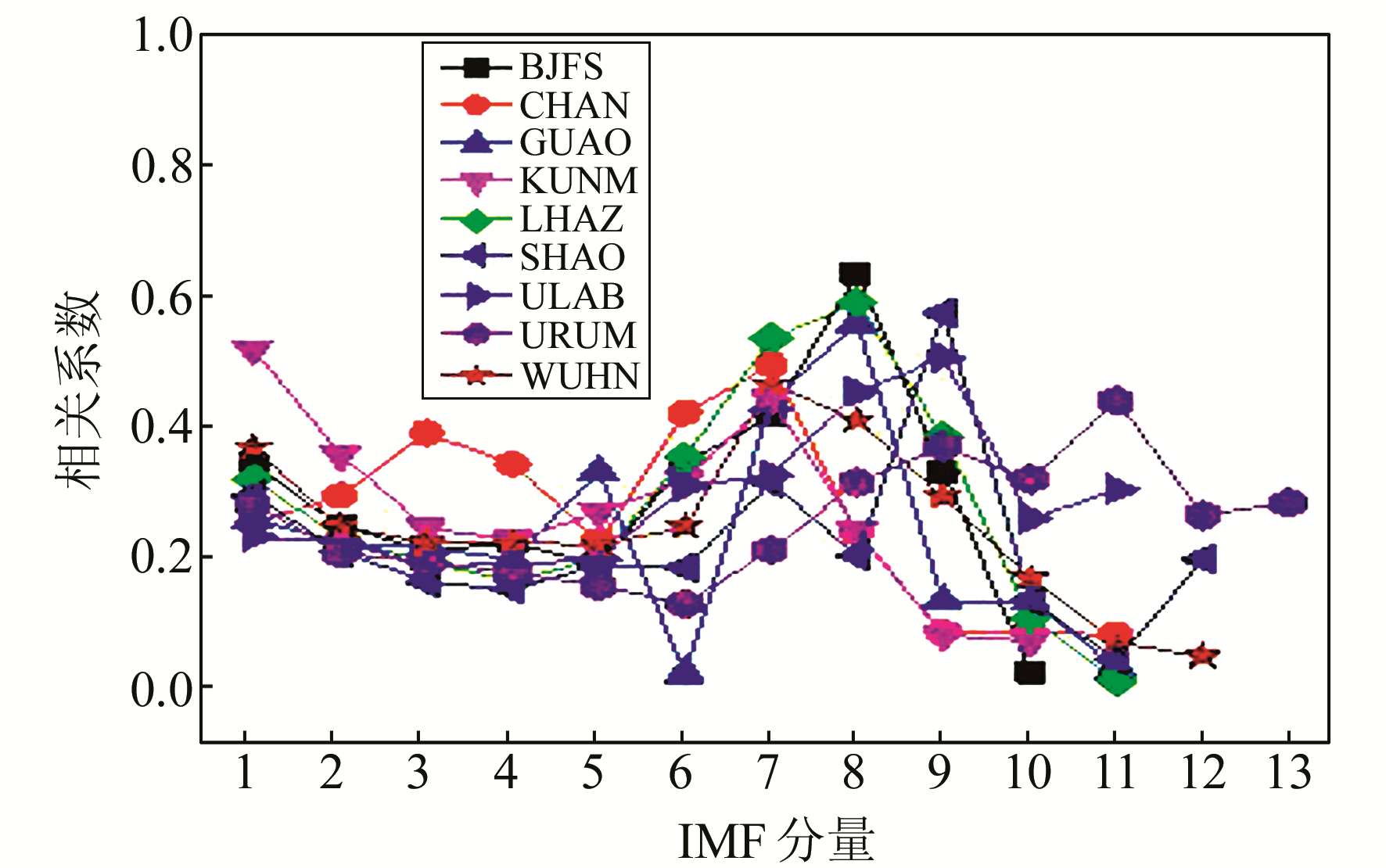
用EMD方法对去线性趋势项后的各IGS站序列作EMD分解,并获得各IMF与相应被分解序列的相关系数,如图 4~6所示。
|
图 4 N方向各IMF相关系数 Fig. 4 Every IMF of north direction component's correlation coefficient |
|
图 5 E方向各IMF相关系数 Fig. 5 Every IMF of east direction component's correlation coefficient |
|
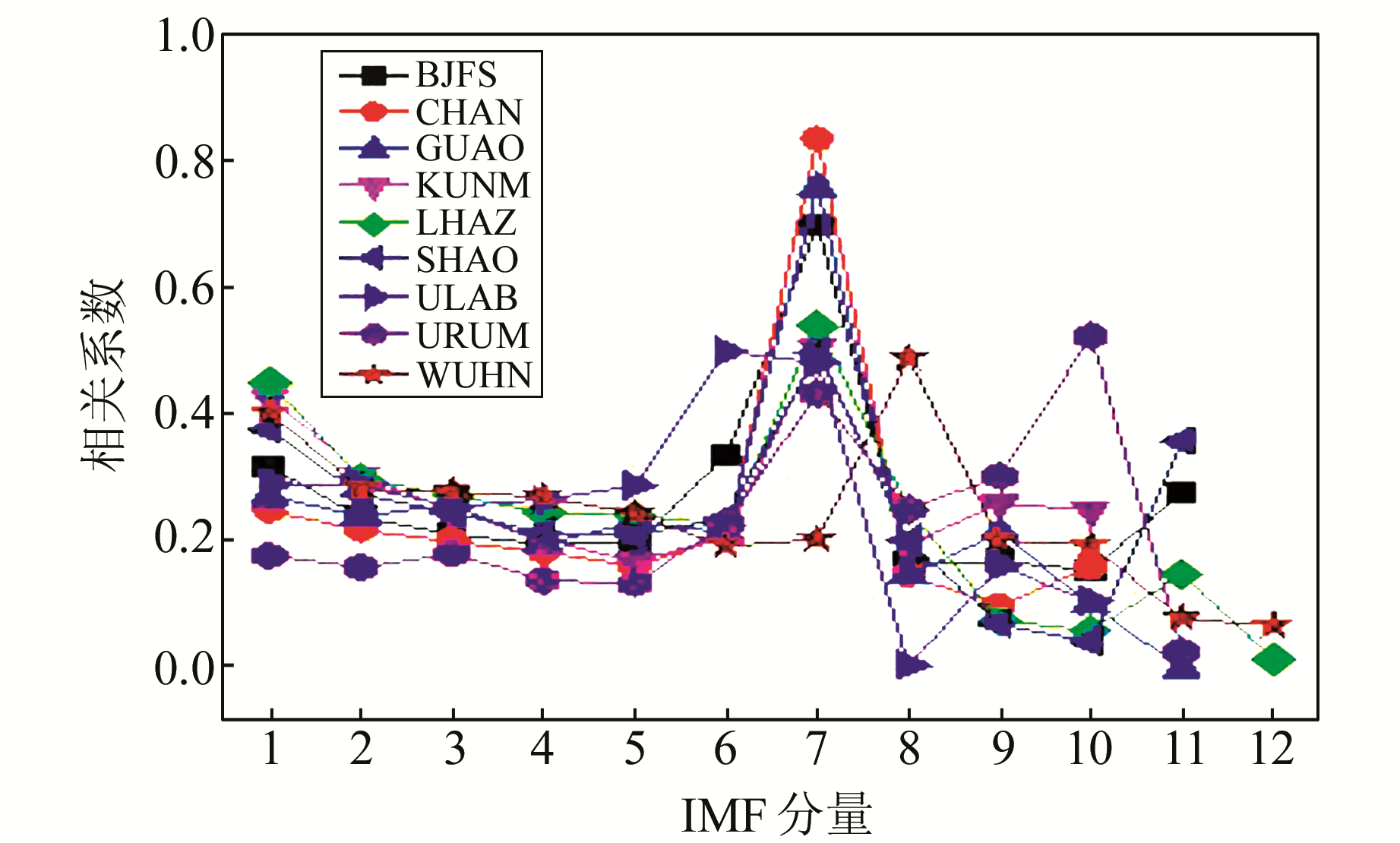
图 6 U方向各IMF相关系数 Fig. 6 Every IMF of up direction component's correlation coefficient |
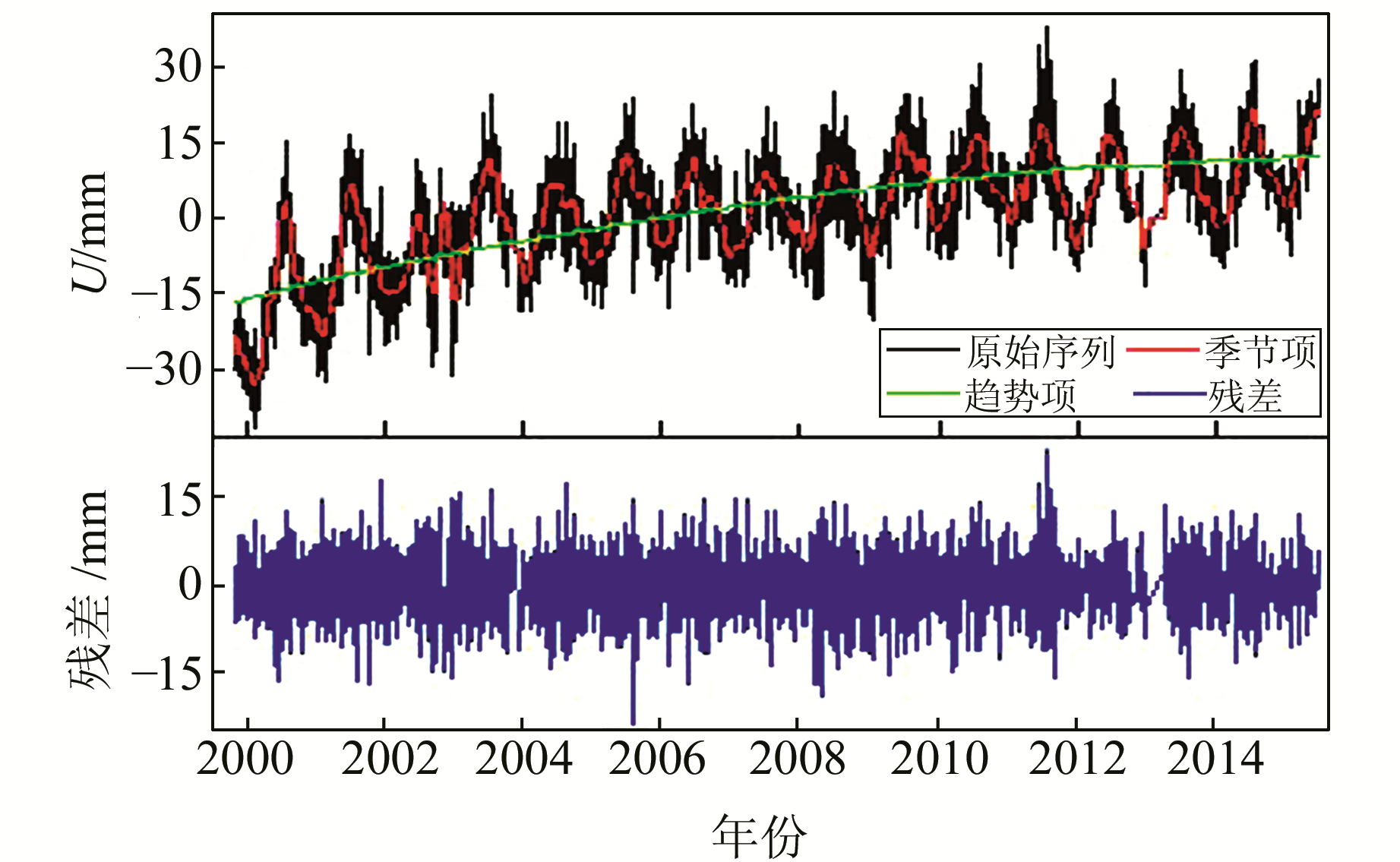
图 4、5表明,N、E方向噪声与信号的分界层主要集中在第4、5个IMF,与原序列一致性较好的IMF则分布在第7~9个分量之间。图 6表明U方向噪声与信号的分界层主要是第4、5个IMF,各IMF中与原序列一致性最好的分量主要是第7个分量。3幅图中也反映在同一个站不同方向上的IMF个数不相同,同一个方向不同站之间所分解的IMF个数也不同,如昆明(KUNM)站,U方向上共分解出10个IMF分量,N方向分解出13个IMF分量。这说明EMD方法分解序列时仅依赖于序列的自身特性;GPS时间序列同一测站各分量序列或不同测站同一方向序列的本身特性均有差异。按照重构方法对BJFS站U方向的序列进行重构,重构后的序列如图 7所示。
|
图 7 BJFS站重构序列 Fig. 7 Reconstruction series of BJFS station |
图 7中原始序列与周期项序列的相关系数为0.85。由图可知,EMD方法获取的周期性变化与原始序列的一致性较好,振幅与原序列的起伏一致,说明周期项的振幅并不是以往分析方法求解的常数值。图中蓝色序列为获取的噪声序列,表现出明显的随机特性,与常用的谐波模型获取的噪声序列相比不包含明显的周期项。
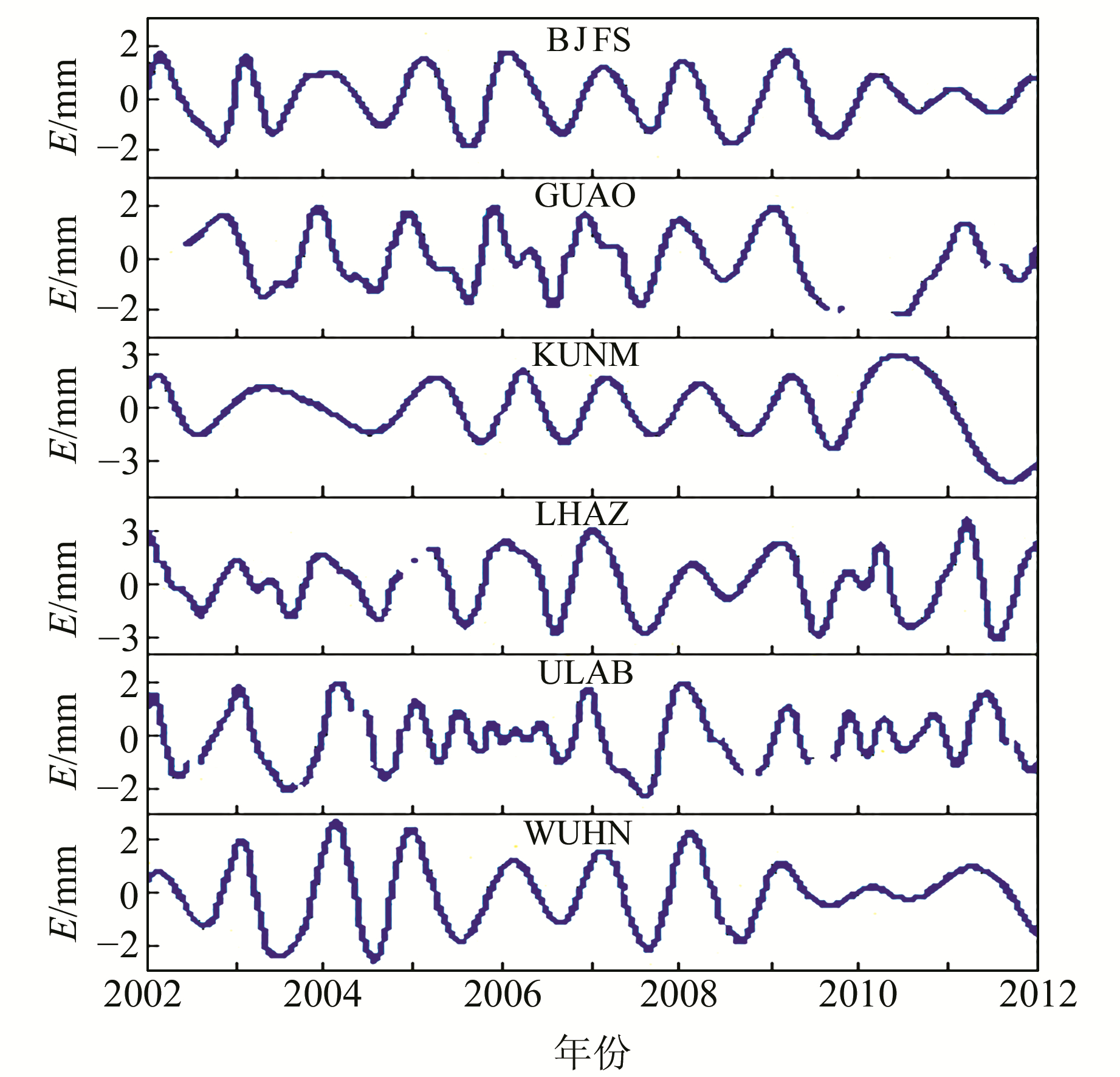
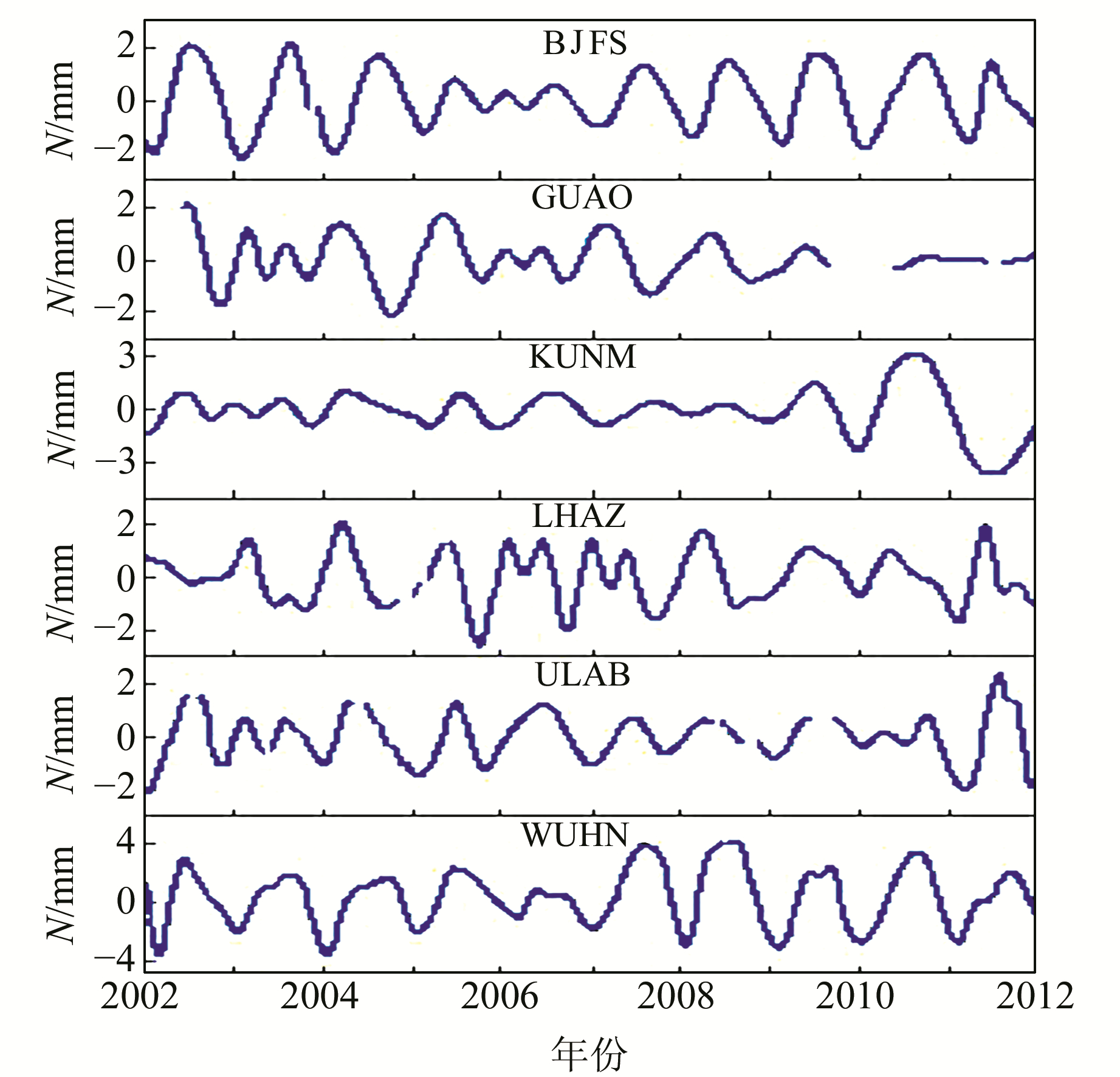
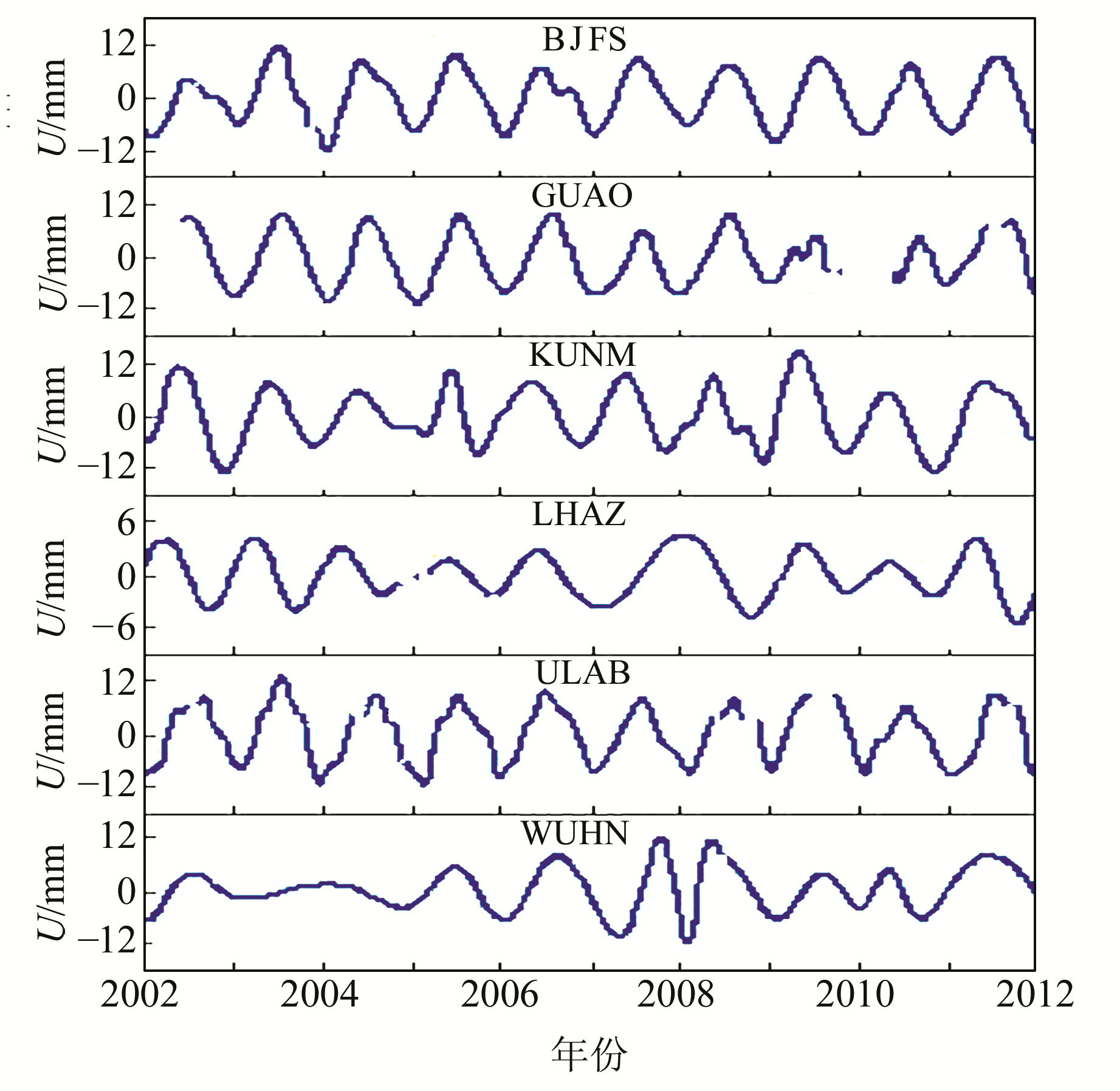
图 8~10为部分站点N、E、U方向上扣除线性趋势项、噪声后所得的降噪序列。由图 8~10更明显地看出各方向均有周期性变化,各站点N、E方向的振幅范围为3~5 mm,U方向振幅范围为6~11 mm。此外各站点季节项的振幅并非常数值,与传统方法获得的振幅值为某一固定常数值相比,本文获取的季节项更能反映出序列的自身运动特性。
|
图 8 E方向降噪序列 Fig. 8 De-noised series of east direction |
|
图 9 N方向降噪序列 Fig. 9 De-noised series of north direction |
|
图 10 U方向降噪序列 Fig. 10 De-noised series of up direction |
为了说明EMD对GPS时间序列降噪的有效性,利用降噪前后序列信噪比的变化、降噪后序列占降噪前序列的能量百分比、被降噪序列与降噪后序列的相关系数等3个参数定量评价降噪效果。其中信噪比Rsn的计算公式如下[6]:
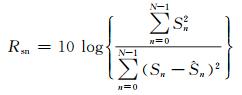
|
(3) |
式中, Sn为原始序列;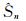
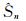
能量百分比E的计算公式为:
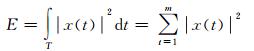
|
(4) |
降噪后序列占原序列的能量百分比Esn定义为:
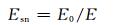
|
(5) |
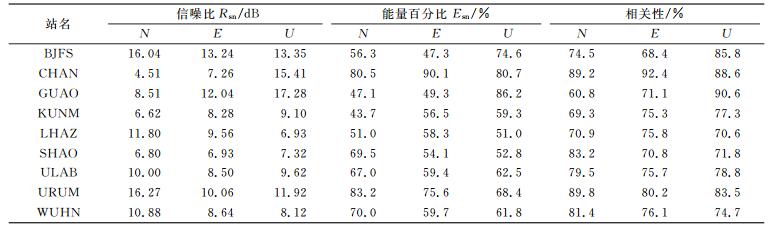
式中,E为原序列能量;E0为降噪后序列的能量。Esn越大,说明降噪后序列与原序列越接近。表 2给出测站各分量的信噪比、能量百分比、相关系数的统计结果。
|
|
表 2 各评价参数统计 Tab. 2 Statistical chart of every assessment parameter |
由式(3)知原始序列的信噪比均为0, 因此表 2中只列出了降噪后序列的信噪比。分析表 2可知:
1) 整体上降噪后各分量序列的信噪比均较高,最高达17.28 dB,均值为10.18 dB;降噪前后能量百分比最高值达90.1%,均值为63.6%;降噪前后序列相关性最高值达92.4%,均值为78%, 说明本文方法整体上降噪效果明显。
2) 因降噪序列的特殊性(均有明显的季节性波动),就单个测站某一分量而言,当序列中噪声较严重时,尤其在N、E方向上,因其季节信号较弱,在降噪时亦受噪声干扰,因此U方向的3个评价参数较N、E方向在数值上普遍偏高。
3) 3个评价参数在某一分量上数值较高的,其降噪后序列季节项也较明显,如GUAO站N方向3个评价参数均小于E、U方向,从图 8~10可看出GUAO站降噪后序列中E、U方向的季节项较N方向更明显。
3 结语本文用EMD方法对原始GPS位置时间序列作降噪分析,有效地从原始序列中分离出线性趋势项、周期项、噪声,达到降噪目的。用降噪后序列的信噪比、降噪后能量占降噪前能量的百分比、降噪前后序列的相关系数以量化的方式证明了用EMD方法对GPS位置时间序列作降噪分析是可行有效的。
| [1] |
王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052 (Wang Min, Sheng Zhengkang, Dong Da'nan. Effects of No-Tectonic Crustal Deformation on Continuous GPS Position Times Series and Correction to Them[J]. Chinese Journal of Geophysics, 2005, 48(5): 1045-1052 DOI:10.3321/j.issn:0001-5733.2005.05.010)
(  0) 0) |
| [2] |
张飞鹏, 董大南, 程宗颐, 等. 利用GPS监测中国地壳的垂向季节性变化[J]. 科学通报, 2002, 47(18): 1370-1377 (Zhang Feipeng, Dong Da'nan, Cheng Zongyi, et al. Crustal Vertical Seasonal Variation in China Observed by GPS[J]. Chinese Science Bulletin, 2002, 47(18): 1370-1377 DOI:10.3321/j.issn:0023-074X.2002.18.003)
(  0) 0) |
| [3] |
姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报:信息科学版, 2010, 35(6): 665-669 (Jiang Weiping, Li Zhao, Liu Wanke, et al. Some Thoughts on Establishment and Maintenance of Terrestrial Reference Frame Considering Non-Linear Variation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 665-669)
(  0) 0) |
| [4] |
袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1372-1384 (Yuan Linguo, Ding Xiaoli, Chen Wu, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 1372-1384 DOI:10.3321/j.issn:0001-5733.2008.05.011)
(  0) 0) |
| [5] |
张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83 (Zhang Hengjing, Cheng Pengfei. Noise Recognition and Extraction of GPS Height Time Series Based on EEMD[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 79-83)
(  0) 0) |
| [6] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1013-1022 (Jia Ruisheng, Zhao Tongbin, Sun Hongmei, et al. Micro-Seismic Signal De-noising Method Based on Empirical Mode Decomposition and Independent Component Analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 1013-1022)
(  0) 0) |
| [7] |
罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报:信息科学版, 2012, 37(04): 450-453 (Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 450-453)
(  0) 0) |
| [8] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series Inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 496-503)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37