2. 中国地震局滇西地震预报实验场办公室,大理市滨海大道,671000;
3. 云南省地震局云县地震台,云南省云县草皮街98号,675803
由于受多种因素影响,变形过程复杂而随机,很难用一种模型合理地反映变形趋势,各单一模型通常会基于某一特定范畴,对变形时间序列进行分析和建模,完成简单的预测[1-2],如灰色模型可对变形原始观测序列的趋势属性进行提取,傅里叶级数可捕捉序列的周期属性,自回归AR算法可模拟序列的随机属性[3]。针对此问题,Bates等[4-5]提出组合预测模型,可综合各单一模型的优缺点,更好地表征变形趋势。组合建模的关键是权重的确定,通常可采用预测误差平方和、误差绝对值之和或最大误差绝对值达到最小为准则的线性权系数确定方法。然而各方法理论复杂、计算繁琐,很难简便地用于客观实际。因此,陈华友等[6-7]基于信息熵建立熵权法,简便地求取权阵。研究表明,熵权法建模过程简单,能够满足组合预测要求。然而,由熵权法确定权重所建立的组合模型,各单一模型在预测过程中被分配到的权重是固定不变的,不能兼顾单一模型在各个时点上的预测能力的强弱,这势必会影响到组合模型的预测精度。鉴于此,本文基于IOWGA算子[6],以各单一模型的预测精度作为预测值的诱导值,按每一期诱导值的大小对单一预测模型进行有序赋权,以保证赋权的合理性。最后将模型应用于变形分析实例中进行验证。
1 熵及熵权法 1.1 熵当系统处于m种不同状态,每种状态出现概率为li(i=1, 2, 3, …, m)时,评价该系统的熵为[6]:
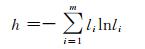
|
(1) |
式中,h为系统的熵值;li为系统出现的概率,且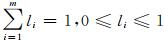
在变形预测中,模型计算值与实测值之间的残差具有不确定性,因此熵值法在组合建模中具有较好的适应性。假设{xt, t=1, 2, …, n}为一实测序列,有m种单一预测模型可对其进行预测,第i种单一预测模型在第t时刻的预测值为xit,则第i种单一预测模型在第t时刻的预测值与实测值的相对误差序列为[6]:
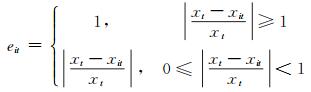
|
(2) |
式中,eit为第i种单一预测模型在第t时刻的预测值与实测值的相对误差序列,i=1, 2, …, m, t=1, 2, …, n。
1) 将单一预测模型的相对误差进行归一化处理,则第i种单一预测模型在第t时刻的预测值与实测值的相对误差比重为:
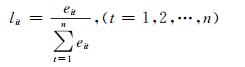
|
(3) |
式中,lit满足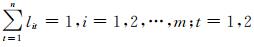
2) 计算第i种单一预测模型相对误差的熵值:
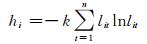
|
(4) |
式中,k为大于零的常数,ln为自然对数,hi≥0, i=1, 2, …, n。对于第i种单一预测模型而言,如果lit全部相等,即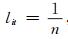

3) 由于系统指标熵值的大小与变异程度成反比,以相对误差作为研究对象,则第i种单一模型变异程度系数可表示为:
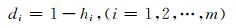
|
(5) |
4) 各模型在组合建模中的权重为:
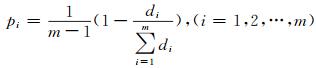
|
(6) |
从式(6)可以看出,单一预测模型的预测误差序列的变异程度与模型在组合建模中的权系数成反比,即变异程度越大,则权系数越小,反之亦然。
2 IOWGA算子假设存在m个二维数组([d1, b1], [d2, b2], …, [dm, bm]),若
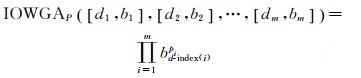
|
(7) |
则称IOWGAP为由诱导值序列d1, d2, …, dm所产生的m维诱导有序加权几何平均算子,简称IOWGA算子[6, 8]。其中,向量P=(p1, p2, …, pm)T是与IOWGAP算子相关的加权向量,且满足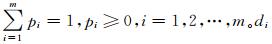
基于熵权法确定权重pi后,建立的组合预测模型为:
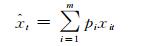
|
(8) |
式(8)属常规的加权组合预测模型,且各单一模型在各个时点的权系数是固定不变的。该赋权方法不符合客观实际,因为每个单一模型在观测序列的各个时点上的表现能力不可能是一成不变的,不可避免地会伴随着跳跃和突变现象的发生,即在某个时点上预测精度较高, 而在另一时点上预测精度较低。如果赋予相等的权重,势必会影响组合模型的预测精度。基于IOWGA算子的权重分配方法,将各单一模型的预测精度作为预测值的诱导值,按每一期诱导值的大小对单一预测模型进行有序赋权,以保证赋权的合理性。令
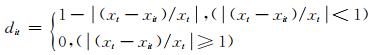
|
(9) |
式中,xt为实际观测序列,xit为第i种单一模型在第t时刻的拟合值,dit表示第i个单一模型在第t时刻的拟合精度,且dit∈[0, 1]。把各单一模型的拟合精度dit当作拟合值xit的诱导值,则m种单一模型第t时刻的拟合精度以及所对应的拟合值就构成了m个二维数组[d1t, x1t], [d2t, x2t], …, [dmt, xmt]。
设向量P=(p1, p2, …, pm)T为各单一模型在基于IOWGA算子的组合模型中的加权向量。将诱导值序列d1t, d2t, …, dmt按从大到小的顺序排列,设d-index(it)为第i个大的诱导值的下标。根据文献[6]可得,由拟合精度序列d1t, d2t, …, dmt作为诱导值建立第t时刻IOWGA组合模型的拟合值为:
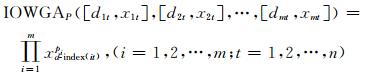
|
(10) |
由式(10)可知,基于IOWGA算子的组合模型的赋权系数与单一模型的种类无关,而与各单一模型在各时点上的拟合精度的大小密切相关,拟合精度成为赋权系数的诱导值。在各个时刻拟合精度较高的单一模型被赋予的权系数也较大,这种赋权思想比较符合实际。
另外,若出现2个以上的拟合精度dit相等时, 通常可以依据t 时刻以前dit相等的这几种单一模型的平均拟合精度作为拟合值xit的次级诱导指标进行有序加权几何平均。
若要进行未来k步的预测,通常用第i种单一模型最近k期的平均拟合精度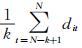
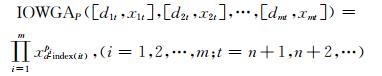
|
(11) |
其中,在预测区间[n+1, n+2, …]上预测精度序列d1t, d2t, …, dmt的大小是由各单一模型在样本区间上近期平均拟合精度来确定的。
熵权-IOWGA组合预测具体求解步骤如下。
1) 采用熵权法确定模型的组合权重向量P=[p1, p2, …, pm]T。
2) 按式(9)计算各单一模型的拟合精度dit,把各单一模型的拟合精度dit当作拟合值xit的诱导值,按式(10)计算组合模型的拟合值。
3) 用第i种单一模型最近k期的平均拟合精度
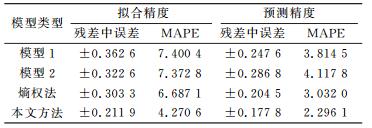
4) 以残差中误差和平均绝对百分比误差(MAPE)作为精度评价指标,评定模型拟合及预测效果。
4 精度评定分别采用残差中误差和平均绝对百分比误差(MAPE)检验模型的拟合及预测能力。
残差中误差计算公式为[9]:

|
(12) |
式中,e为实测值与预测值的残差,n为预测周期。残差中误差反映的是一组预测值的残差分布情况,可用来评价预测模型的预测精度,残差中误差越小,预测精度越高。
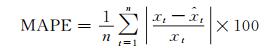
|
(13) |
MAPE的精度评价指标见表 1。
|
|
表 1 精度分级 Tab. 1 Level of MAPE |
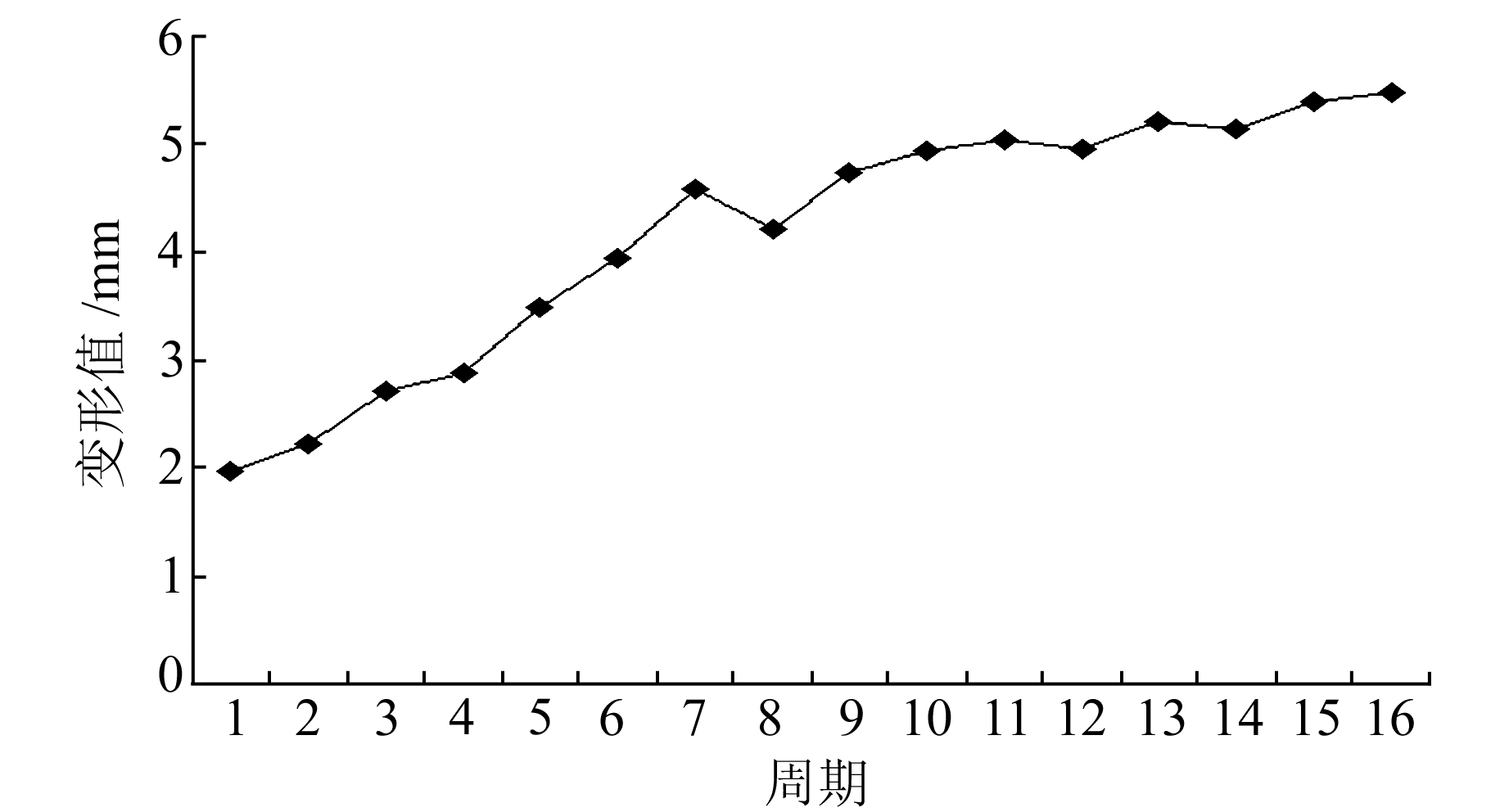
以某尾矿库初期坝的沉降监测数据为例进行实验。该尾矿坝共布设了8个水准点,由于各监测点的变化规律大致相同,本文选择其中的A5点进行分析(图 1)。
|
图 1 尾矿坝变形沉降序列 Fig. 1 Settlement sequence of tailings dam |
由图 1可看出,该点1~3期、5~7期、9~11期变化较为平稳,其他几期呈现跳跃式浮动。可见,该点变形不稳定,随机性变化较强,呈非线性变化趋势。显然,如果用单一模型预测,很难得到较优的全局预测值。
本文采用由F检验进行模型阶数判断(模型阶数p=3)的自回归AR(3)模型(模型1)、BP神经网络(模型2)、熵权法确定权重的组合模型(熵权法)作为对比方案,前12期作为拟合区间,后4期作为预测区间,基于熵权法所求得的2组模型的权重为p1=0.738 9,p2=0.261 1。以模型1和模型2的拟合及预测精度作为诱导值,进行有序赋权,建立基于熵权-IOWGA算子的变权组合模型(本文方法),4种模型的拟合及预测结果分别见表 2(单位mm)、表 3(单位mm)。
|
|
表 2 模型拟合值与实测值对比 Tab. 2 Comparison among the fitting values and the measured values of different models |
|
|
表 3 模型预测值与实测值对比 Tab. 3 Comparison among the predictive values and the measured values of different models |
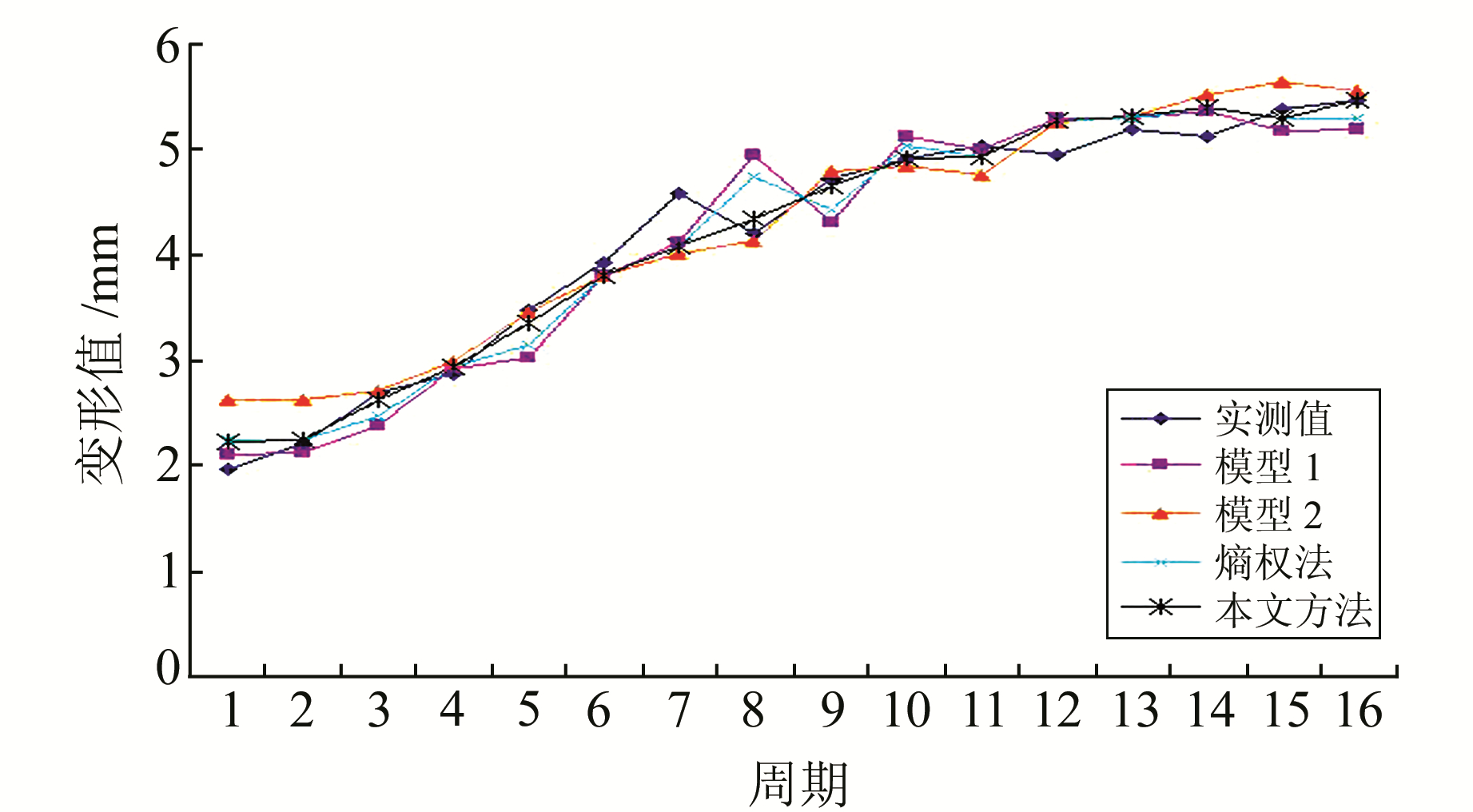
|
图 2 拟合及预测曲线 Fig. 2 Fitting and predicting curves |

|
图 3 各模型残差分布比较 Fig. 3 Comparison among residual curves of different models |
由表 2、3可知,本文方法拟合及预测残差波动性较小,最大残差和最小残差分别为0.49 mm和0.01 mm;熵权法为0.53 mm和0.04 mm;模型1为0.74 mm和0.03 mm;模型2为0.65 mm和0.01 mm。和其他3种模型比较可知,本文方法拟合及预测过程更为稳定,优于熵权法和各单一模型,预测结果更加符合客观变形值。
为了更好地评定模型效果,以残差中误差和平均绝对百分比误差(MAPE)作为精度评价指标,各模型拟合及预测精度见表 4(单位mm)。
|
|
表 4 各模型精度比较 Tab. 4 Comparison among the accuracy of different models |
由表 3可以发现,本文方法和熵权法的残差中误差和MAPE值均小于模型1、模型2,说明两种组合方法拟合、预测效果更好。与熵权法相比,本文方法模型拟合及预测误差更小,精度更高,说明基于熵权-IOWGA算子的变权组合模型赋权方法更加合理,模型拟合及预测更加有效。
6 结语本文将熵权法和IOWGA算子相结合,构建基于熵权-IOWGA算子的变权组合模型,以克服熵权法组合预测过程中组合权重分配固定不变的缺点。通过IOWGA算子对组合权重进行分配,即以各单一模型的拟合、预测精度作为诱导值,按每一期诱导值的大小对单一模型进行有序赋权,并将其应用到实际工程中,验证了本文所提出的组合预测模型的有效性和合理性。实验结果表明,基于熵权-IOWGA算子的变权组合模型赋权过程合理,模型拟合、预测精度更高,更加适用于变形分析预测过程。
| [1] |
文鸿雁. 基于小波理论的变形分析模型研究[J]. 测绘学报, 2005, 34(2): 186-187 (Wen Hongyan. Research on Deformation Analysis Model Based upon Wavelet Transform Theory[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 186-187 DOI:10.3321/j.issn:1001-1595.2005.02.018)
(  0) 0) |
| [2] |
卢骏, 戴吾蛟, 章浙涛. 大坝变形变系数回归建模[J]. 武汉大学学报:信息科学版, 2015, 40(21): 139-142 (Lu Jun, Dai Wujiao, Zhang Zhetao. Modeling Dam Deformation Using Varying Coefficient Regressing[J]. Geomatics and Information Science of Wuhan University, 2015, 40(21): 139-142)
(  0) 0) |
| [3] |
高宁, 高彩云. 变形监测数据组合预测的串联与并联模式研究[J]. 大地测量与地球动力学, 2013, 33(3): 116-120 (Gao Ning, Gao Caiyun. On Model and Forecast of Deformation Monitoring Data Based on Series and Parallel Combination Prediction[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 116-120)
(  0) 0) |
| [4] |
Bates J M, Granger C W J. The Combination of Forecasts[J]. Operations Research Quarter1y, 1969, 20(4): 451-468 DOI:10.1057/jors.1969.103
(  0) 0) |
| [5] |
Granger C W J. Combining Forecasts-Twenty Years Later[J]. Journal of Forecasting, 1989, 8(3): 167-173 DOI:10.1002/(ISSN)1099-131X
(  0) 0) |
| [6] |
陈华友. 组合预测方法有效性理论及其应用[M]. 北京: 科学出版社, 2008 (Chen Huayou. Combination Forecast Method and Its Application[M]. Beijing: Science Press, 2008)
(  0) 0) |
| [7] |
陈华友. 熵值法及其在确定组合预测权系数中的应用[J]. 安徽大学学报:自然科学版, 2003, 27(4): 1-6 (Chen Huayou. Entropy Method and Application to Determine Weights of Combination Forecasting[J]. Journal of Anhui University Natural Science Edition, 2003, 27(4): 1-6)
(  0) 0) |
| [8] |
闫滨, 周晶, 高真伟. 一种基于IOWGA算子的大坝安全监控[J]. 岩石力学与工程学报, 2007, 26(S2): 4074-4078 (Yan Bin, Zhou Jing, Gao Zhenwei. An IOWGA Operator-Based Dam Safety Monitoring Combination Forecasting Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S2): 4074-4078)
(  0) 0) |
| [9] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版, 2009 (Survey Adjustment Research Group, School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [10] |
任超, 梁月吉, 庞光锋, 等. 最优非负变权组合模型在大坝变形中的应用[J]. 大地测量与地球动力学, 2014, 34(6): 162-166 (Ren Chao, Liang Yueji, Pang Guangfeng, et al. Application of the Optimal Non-Negative Variable Weight Combination Model for Monitoring Dam Deformation[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 162-166)
(  0) 0) |
2. Office of the Western Yunnan Earthquake Prediction Study Area, CEA, Binhai Road, Dali 671000, China;
3. Yunxian Seismic Station of Yunnan Earthquake Agency, 98 Caopi Street, Yunxian 675803, China
 2017, Vol. 37
2017, Vol. 37