2. 东华理工大学测绘工程学院,南昌市广兰大道418号,330013;
3. 61234部队,乌鲁木齐市,830006
机器学习新算法——相关向量机(RVM)具有小样本、非线性、参数少、稀疏性高等特点,且核函数不需要满足Mercer条件。不少学者基于RVM建立了大坝变形预测模型[1-4],结果证实RVM应用于变形预测能取得较好的精度。但RVM在边坡变形预测领域还未开展相关研究,且标准RVM为单输出模型,不能处理多输出边坡变形预测问题。
鉴于边坡变形过程的复杂性及RVM在处理非线性复杂系统问题的优势,本文对标准单输出RVM进行拓展,建立多输出相关向量机(MRVM),利用PSO优化其参数,并提出基于MRVM的多输出边坡变形预测新模型。通过对MRVM的精度及计算效率进行分析,验证MRVM用于解决多输出边坡变形问题的有效性。
1 多输出相关向量机对于MRVM回归模型,设训练数据集{xn, tn}n=1N,xn∈Rq为输入向量,q为输入维数,tn∈RM为输出向量, M为输出维数,N为训练样本数。目标值tn可表示为:
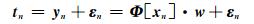
|
(1) |
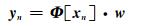
|
(2) |
式中,yn=[yn1, …, ynM]为MRVM回归模型的第n组样本对应的M维多变量输出;εn为观测噪声,εn为零均值、方差为B=diag(β1, …βm, …βM)的高斯分布;w为权矩阵,w=[w1, …, wm, …wM],wm=[wm0,wm1, …, wmN]T;Φ[xn]=[1, K(xn, x1), …, K(xn, xN)],K(xi, xj)为核函数。
楼俊钢等[5]通过对RVM的多种核函数进行对比,证实高斯核函数RVM具有更好的预测精度。因此,本文选择高斯核函数作为MRVM的核函数:
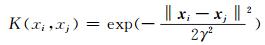
|
(3) |
式中,γ为核函数宽度,是MRVM算法需要用户设置的唯一参数。
为了避免使用极大似然函数方法求解w与B时出现“过拟合”,根据稀疏贝叶斯原理,假定w服从零均值高斯先验分布:
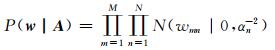
|
(4) |
式中,wmn为w的元素;A=diag(α1-2, …, αN-2)为w的超参数。
因此,w的似然分布为:
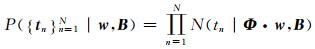
|
(5) |
式中,Φ=[Φ[x1], …, Φ[xN]]T。
w的后验概率分布可表示为:
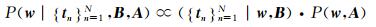
|
(6) |
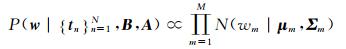
|
(7) |
式中,μm=βm-1ΣmΦTτm为wm的期望,τm=[t1m, …, tNm]为训练数据集{xn, tn}n=1N中第m维目标向量,Σm=(βm-1ΦTΦ+A)-1为wm的方差。
最后,通过最大化目标函数的边缘似然函数,估计A与B[6]。基于A与B,最终确定权矩阵为w′,并将其代入式(2),建立MRVM回归模型。由于A中的αm绝大部分趋近无穷大,与其对应的权值趋于零,使得MRVM具有很好的稀疏性。对于新的输入x*,MRVM模型预测相应的输出为:
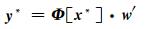
|
(8) |
MRVM通过对训练数据集进行学习确定w′,并代入式(8)建立边坡变形影响因素与多个变形量之间的函数关系,从而建立基于MRVM的多输出边坡变形预测模型。由MRVM理论可知,MRVM在求解w′之前需要设置参数γ,其设置是影响MRVM预测精度的关键问题。因此,本文采用具有较好全局搜索能力的智能优化算法——粒子群优化算法(PSO)确定MRVM的参数γ,减少由于MRVM的参数不合理对其预测精度的影响。
以文献[7]中收集的40例大型干坞边坡变形数据为例,以土体强度c/kPa和φ/(°),无护坡暴露时间tr/h,边坡坡率n,沿长度方向每层分步开挖步长L/m,分层开挖层数N,分层开挖深度he/m,降水深度hd/m和坡顶超载q/kPa为边坡变形影响因素,d/mm为坡顶水平变形,s/mm为坡顶地表沉降。边坡变形的影响因素作为MRVM的输入,坡顶水平变形及坡顶地表沉降作为模型输出,并取前30个样本建立训练数据集,后10个样本作为测试集。以MRVM的参数γ作为PSO算法的粒子位置,利用交叉验证法建立适应度计算函数,通过不断迭代更新粒子,最后将适应度最高的粒子位置作为MRVM的最优参数γbest,并利用该参数建立基于MRVM的边坡变形预测模型。具体优化过程如下。
1) 训练数据集归一化处理,设置PSO参数。参考文献[8],通过试算确定粒子数量POPsize=30,惯性权重系数wpso=0.7,学习因子c1=2, c2=2,粒子最大进化代数Kmax=100。
2) 初始化。随机产生一组粒子的初始位置和速度,T=1为粒子迭代次数。
3) 用适应度函数计算粒子的适应度。采用留一交叉验证法建立粒子适应度计算函数:每次选取训练集中不同的1个样本作为测试集,其余m-1个样本作为训练集,以粒子的位置为MRVM的参数,对测试数据进行预测。重复m次以上操作,得到m个测试数据的预测结果,并将预测结果的均方根误差的倒数作为粒子的适应度。
4) 确定每个粒子的最优位置pbesti(T)和粒子群全局最优位置gbest(T)。pbesti(T)为第i个粒子经历T次迭代后获得的最优位置(搜索粒子i获得最大适应度时粒子的位置);gbest(T)为全部粒子经历T次迭代后获得的最优位置(搜索全部粒子中适应度最大粒子的位置)。
5) 按式(9)和(10)更新粒子的速度和位置:
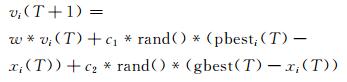
|
(9) |
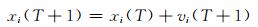
|
(10) |
6) 判断T是否小于Tmax。如果T < Tmax,T=T+1,进入步骤3);如果T≥Tmax,粒子群停止迭代。此时,gbest(T)记录的粒子位置就是MRVM的最优参数γbest,具体参数见表 2。
|
|
表 2 边坡坡顶水平变形预测结果及其精度 Tab. 2 Prediction results and the accuracy of the horizontal deformation of slope |
7) 基于最优参数γbest与训练数据集计算w′,代入式(9)建立基于MRVM的多输出边坡变形预测模型。
3 结果分析为验证基于MRVM的多输出边坡变形预测模型的精度及计算效率,同时基于BP神经网络、支持向量机(SVM)、RVM建立边坡坡顶水平变形与地表沉降变形预测模型,并均基于PSO采用同样的方式优化各变形预测模型的参数,具体参数见表 1。基于以上各模型,分别对测试数据集的坡顶水平变形及坡顶地表沉降变形进行预测,并利用最大绝对误差百分比(MAXAPE)、平均绝对误差百分比(MAPE)、均方误差(MSE)等精度指标评价各模型结果的精度,具体预测结果及其精度如表 2、3所示。
|
|
表 1 边坡变形预测模型的参数 Tab. 1 Parameters of prediction model of slope deformation |
|
|
表 3 坡顶地表沉降变形预测结果及其精度 Tab. 3 Prediction results and the accuracy of settlement deformation of slope |
由表 2、3可知,MRVM对坡顶水平变形及坡顶地表沉降变形进行预测的精度与BP神经网络、支持向量机(LS-SVM)、标准RVM比较有较大幅度提高,且MRVM将坡顶水平变形及坡顶地表沉降变形进行统一处理,简化了建模难度及过程,是一种精度较高的边坡变形预测新模型。
为比较MRVM、BP神经网络、LS-SVM、RVM的计算效率,基于表 1参数,各模型对测试数据的坡顶水平变形及坡顶地表沉降变形进行50次重复运行,并计算各模型的平均耗时,具体数据如表 4所示。
|
|
表 3 计算效率统计 Tab. 3 Statistical table of computational efficiency |
由表 4可知,MRVM与BP神经网络为多输出模型,不需要对每个输出变量单独建立模型,有效简化了建模过程。但BP神经网络训练模型耗时较多,计算效率较差。SVM、RVM为单输出模型,需要独立建立边坡坡顶水平变形及坡顶地表沉降变形模型,增加了建模难度和复杂性,同时也增加了模型的计算量。因此,MRVM比BP神经网络、SVM、RVM具有更高的计算效率。
4 结语对标准RVM进行拓展,建立MRVM算法。基于MRVM建立多输出边坡变形预测新模型,并利用PSO优化MRVM参数。通过对结果进行精度及计算效率分析,得到以下结论:
1) MRVM对边坡的水平变形与沉降变形预测的精度优于单输出RVM,表明MRVM对标准RVM进行拓展方法的有效性,没有造成精度损失。MRVM的预测精度明显优于BP神经网络、SVM,证实MRVM对边坡的水平与沉降变形具有较高的预测精度。
2) 建立二输出MRVM,实现同时预测边坡坡顶水平变形及坡顶地表沉降变形,可避免重复建立边坡坡顶水平变形模型及坡顶地表沉降变形模型,有效简化建模过程及难度,提高计算效率。MRVM边坡预测所耗时间远小于BP神经网络、SVM、RVM,证实MRVM在取得较高精度的同时,计算速度也较快。
| [1] |
Tipping M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244
(  0) 0) |
| [2] |
向杰. 基于混合核RVM理论的大坝变形监控优化模型[J]. 水电能源科学, 2015, 33(5): 59-89 (Xiang Jie. Dam Deformation Monitoring Optimization Model Based on Hybrid Kernel RVM Theory[J]. Water Resources and Power, 2015, 33(5): 59-89)
(  0) 0) |
| [3] |
屠立峰, 包腾飞, 唐琪, 等. 基于PSO-RVM-ARIMA的大坝变形预警模型[J]. 中国农村水利水电, 2015(6): 112-115 (Tu Lifeng, Bao Tengfei, Tang Qi, et al. Dam Deformation Forecasting Based on PSO-RVM-ARIMA Model[J]. China Rural Water and Hydropower, 2015(6): 112-115 DOI:10.3969/j.issn.1007-2284.2015.06.028)
(  0) 0) |
| [4] |
杜传阳, 郑东健. 相关向量机理论在大坝变形监测模型中的方法研究[J]. 武汉大学学报:工学版, 2015, 48(5): 652-657 (Du Chuanyang, Zheng Dongjian. Research on Methods of Dam Deformation Monitoring Model Based on RVM Theory[J]. Engineering Journal of Wuhan University, 2015, 48(5): 652-657)
(  0) 0) |
| [5] |
楼俊钢, 蒋云良, 申情, 等. 软件可靠性预测中不同核函数的预测能力评估[J]. 计算机学报, 2013, 36(6): 1303-1311 (Lou Jungang, Jiang Yunliang, Shen Qing, et al. Evaluating the Prediction Performance Kernel Based Software of Different Kernal Functions in Reliability Models[J]. Chinese Journal of Computers, 2013, 36(6): 1303-1311)
(  0) 0) |
| [6] |
Thayananthan A. Template-Based Pose Estimation and Tracking of 3D Hand Motion[D]. Cambridge: University of Cambridge, 2005
(  0) 0) |
| [7] |
关秦川, 张志勇, 冯浩. 大型干坞边坡变形及其神经网络预测模型[J]. 西南交通大学学报, 2004, 39(2): 157-161 (Guan Qinchuan, Zhang Zhiyong, Feng Hao. Artificial Neural Network Forecast Model for Slope Deformation of Large-Scale Dry-Dock[J]. Journal of Southwest Jiaotong University, 2004, 39(2): 157-161 DOI:10.3969/j.issn.0258-2724.2004.02.006)
(  0) 0) |
| [8] |
Kennedy J, Eberhart R C.Particle Swarm Optimization[C].IEEE International Conference on Neural Networks, Perth, 1995
(  0) 0) |
2. Faculty of Geomatics, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
3. 61243 Troops of PLA, Urumqi 830006, China
 2017, Vol. 37
2017, Vol. 37





