在桥梁变形预测中,许多学者对预测方法的适用性进行了探讨。胡小伍[1]利用卡尔曼滤波对变形监测数据进行去噪处理,再利用模糊神经网络对数据进行预测,用实例检验该方法对预测精度有较大的改善;刘娜等[2]利用时间序列法对桥梁变形进行预测,证实该方法具有较高的预测精度,且适用性较强,能为桥梁变形进行有效的预警;张全良等[3]将卡尔曼滤波和双曲线法综合应用到桥墩变形预测中,并通过对比分析,验证该预测模型的有效性。上述研究虽对桥梁变形预测积累了一定的实践经验,但均采用较为单一的预测方法,缺乏桥梁变形组合预测方面的研究。由于不同预测方法所需的信息具有一定的差异,对实例的适用性也不同,因此采用组合预测能实现多种方法的信息整合[4],提高预测精度及稳定性。在组合预测研究方面,已有相关学者将其应用到岩土工程的其他领域。隆然等[5]采用多种定权和非定权的组合预测方法对滑坡变形进行预测,实例验证组合预测的精度较单项预测有较大的提高;叶超等[6]将BP神经网络和支持向量机进行结合对滑坡变形进行复合式预测,证实该方法的预测误差较小,适用性较好。上述研究说明,组合预测对提高预测精度及稳定性具有较大的作用。本文将组合预测引入桥梁变形预测过程中,以提高预测精度为目的,为桥梁变形预测提供一种新的思路。
1 基本原理 1.1 预测思路受环境因素的影响,桥梁变形具有明显的非线性特征。为提高桥梁变形预测的精度,本文基于组合预测思路,利用MC误差修正预测结果,使实测值与预测值更为接近,主要思路如下。
1) 采用GM(1, 1)、LS-SVM、RBF及BP神经网络模型对桥梁变形进行单项预测,对比不同预测模型在实例中的预测效果,并为组合预测提供数据基础。
2) 采用若干定权、非定权组合方法对单项预测结果进行组合预测,提高变形预测结果的稳定性及精度。
3) 利用MC对组合预测结果进行误差修正,减小预测误差,进一步提高预测精度。
1.2 单项预测模型1) GM(1, 1)
将桥梁变形的n个监测样本表示为x(0),即
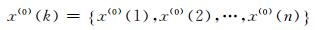
|
(1) |
式中, k=1, 2, …, n。
利用对监测序列的一阶累加消除原始样本的随机性和波动性,将一阶累加序列x(1)表示为:
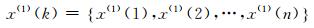
|
(2) |
其中,相应节点的求解过程表示如下:
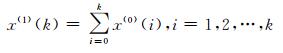
|
(3) |
灰色模型的一阶微分方程为:
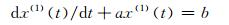
|
(4) |
上述微分方程参数a、b应满足最小二乘估计,即
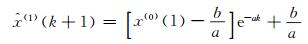
|
(5) |
进一步,通过微分方程的特解反推各节点的预测值:
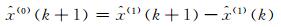
|
(6) |
2) LS-SVM(最小二乘支持向量机)
若桥梁变形序列x={xn},变形节点xi+p与前p个变形值之间的关系可表示为:
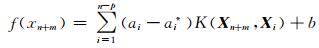
|
(7) |
式中,f(xn+m)为第n+m时刻的变形函数值,Xi为第p+i时刻前p个时刻的变形值,Xn+m为在n+m时刻前p个时刻的变形值,a、a*、b为二次规划参数。
二次规划参数的求解过程为:
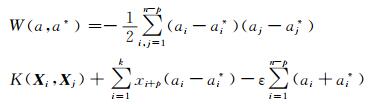
|
(8) |
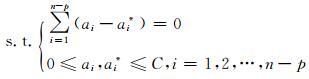
|
(9) |
在其应用过程中,对使用者的经验要求较高,很大程度上降低了该模型的使用效率。为解决上述问题,将最小二乘法引入到支持向量机的参数优化中,将传统支持向量机的不等式约束转变为等式约束,提高对参数优化的能力,达到提高预测精度的目的。
3) RBF和BP神经网络
神经网络预测是模拟动物神经网络的特征,进行多重分布式预测的数学处理方法,具有很强的空间映射和非线性预测能力。其中,RBF和BP神经网络是最为常用的神经网络方法,均可采用三层网络结构,利用正、反向传播修正节点之间的连接权值,使输出值达到期望的目标。由于上述2种神经网络已被广泛应用,对其基本原理不再赘述。
1.3 组合预测模型为充分探讨不同组合预测模型的有效性,采用定权和非定权组合预测模型对单项预测结果进行组合,达到组合预测的目的。定权组合预测包含误差平方和与变异系数法,而非定权组合预测包含RBF和BP神经网络。其中,非定权组合预测模型是以前期单项预测模型为输入层,以对应时刻的实测值为输出层进行训练,进而实现对后期变形的预测。
1.4 误差修正模型为进一步提高预测精度,采用马尔可夫链(Markov chain,MC)对组合预测结果进行误差修正。该方法的基本原理是对预测的相对误差进行区间划分,表示为S=[Sn],n=1, 2,…,n。同时,不同子区间可代表一种状态,而i到j状态转变概率可表示为:
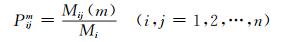
|
(10) |
式中,Mi为第i状态的个数,Mij(m)为状态转移次数。
进一步利用位移转移矩阵即可实现误差修正,并将预测值表示为:
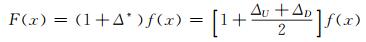
|
(11) |
式中,F(x)为修正值,Δ*为平均相对误差,ΔU、ΔD为相对误差的上、下限参数,f(x)为预测值。
考虑到不同组合预测模型的组合结果具有一定的差异,对组合预测中的最优结果进行误差修正。
2 实例分析 2.1 实例概况实例来源于文献[2]。某桥梁施工过程中,对其桥墩变形进行监测,监测时间是2009-08~2010-05,监测周期是每周1次,共监测40个周期,其累计变形-时间曲线如图 1所示。

|
图 1 桥梁累计变形-时间曲线 Fig. 1 Accumulative deformation time curve of bridge |
由图 1可见,桥梁桥墩前期变形较大,后期变形较平缓。为进一步分析桥梁的变形特征,对其变形速率进行统计,见图 2。由图 2可知,桥梁变形速率起伏波动变化较大,总体呈前期变形速率波动较大、后期较小的规律,说明外界环境因素对桥梁变形具有较大的影响,其中最大变形速率为7.35 mm/周期。

|
图 2 桥梁速率-时间曲线 Fig. 2 Speed time curve of bridge |
将速率比参数引入到桥梁的速率特征分析中。速率比是各时刻的变形速率与平均速率之比,能有效评价各时刻速率相对平均速率的变化程度。结合实例,将速率比进行区间划分,并对各区间进行定级,见表 1。
|
|
表 1 速率比分级 Tab. 1 Speed ratio classification |
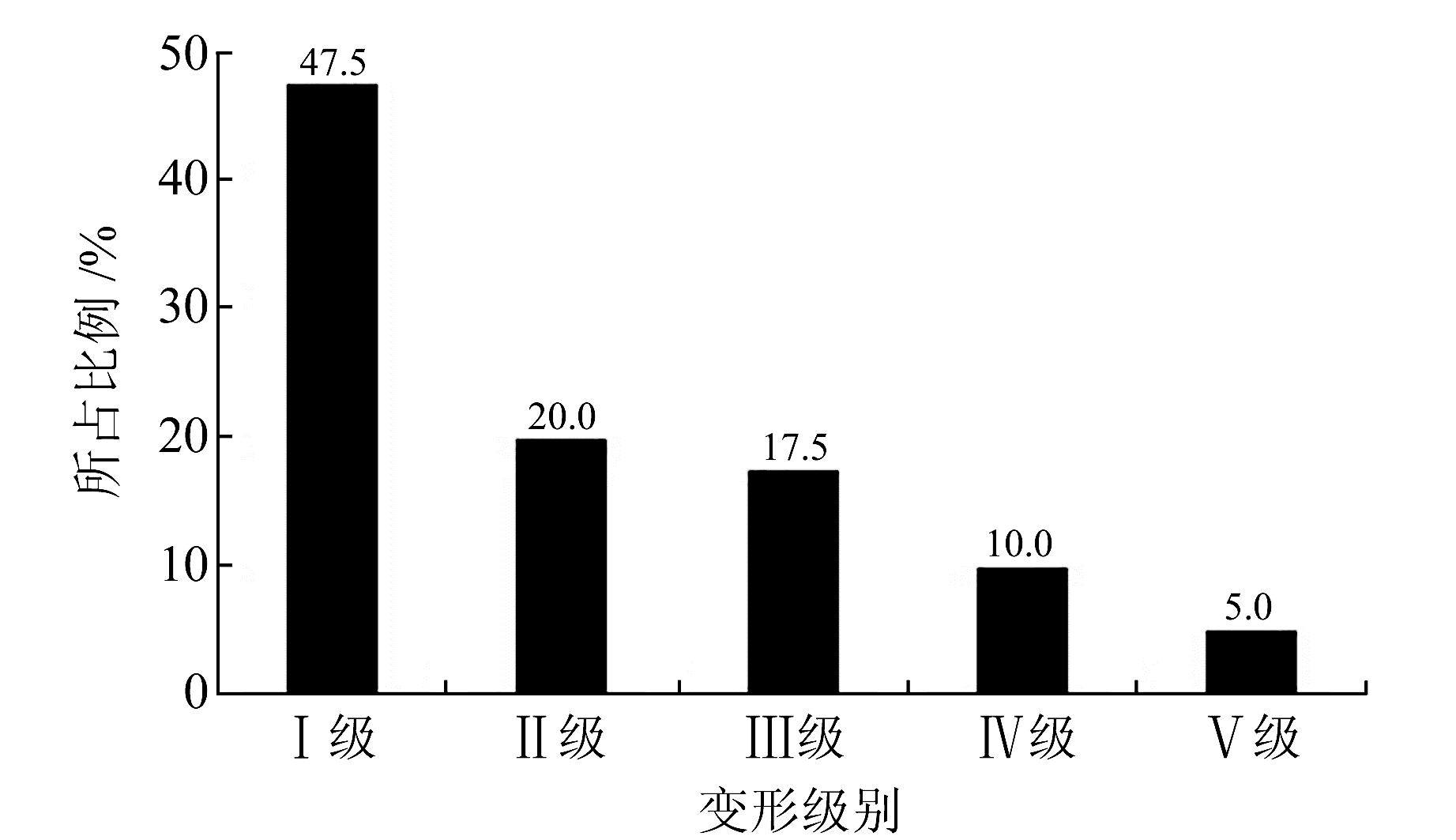
对桥梁变形速率比进行统计,得出桥梁速率比分级情况,如图 3所示。由图 3可知,桥梁变形多(占47.5%)处于强减速阶段,结合图 1进一步得出桥梁后期变形波动性减弱且趋于稳定;同时,桥梁加速变形阶段所占的比例明显小于减速变形阶段的比例,且加速变形阶段多位于变形前期。
|
图 3 桥梁变形速率比分级 Fig. 3 Bridge deformation rate ratio classification |
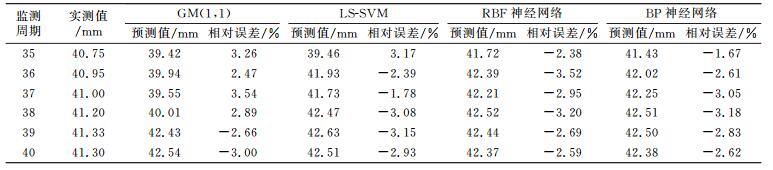
结合本文预测思路,采用GM(1, 1)、LS-SVM、RBF及BP神经网络模型对桥梁变形进行单项预测。同时,将35~40期的变形数据作为检验样本,预测结果如表 2所示。
|
|
表 2 单项预测结果统计 Tab. 2 Statistics of individual forecast results |
对比不同预测模型的结果可知,不同预测模型的预测结果具有较大的差异,说明不同预测模型所含的信息具有一定差异。为进一步分析各模型在本文实例中的适用性和有效性,对各预测模型相对误差的特征参数进行统计,结果如表 3所示。由表 3可知,最大相对误差为GM(1, 1)预测的3.54%,最小相对误差为BP神经网络预测的1.67%。同时,考虑到变异系数包含相对误差的平均值和标准差信息,将其引入到单项预测模型适用性的特征评价过程中。其中,RBF及BP神经网络预测的变异系数相当,且明显小于GM(1, 1)和LS-SVM的变异系数,说明后2种方法的预测结果具有更大的离散程度,且GM(1, 1)预测结果的离散程度最高,预测结果相对最差。
|
|
表 3 单项预测特征参数统计 Tab. 3 Statistics of characteristic parameters of individual forecasting |
采用定权和非定权模型对桥梁变形进行组合预测,组合预测过程及结果分析如下。
1) 定权组合预测
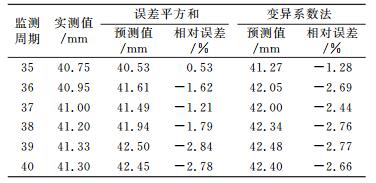
定权组合预测包含误差平方和与变异系数法,其中误差平方和法的组合权重为[0.226 4 0.258 8 0.238 5 0.276 3];变异系数法的组合权重为[0.069 8 0.081 1 0.492 9 0.356 3],结果如表 4所示。由表 4可知,2种方法较单项预测均不同程度地提高了预测精度,说明组合预测的有效性。其中,误差平方和相对误差绝对值的最大值为2.84%,最小值为0.53%;变异系数法相对误差绝对值的最大值为2.77%,最小值为1.28%,两者对比差异较为明显,前者相对较优。
|
|
表 4 定权组合预测结果统计 Tab. 4 Statistical results of fixed weight combination forecasting |
2) 非定权组合预测
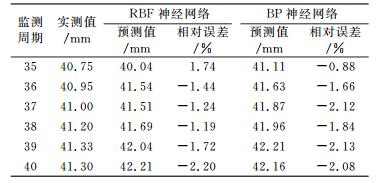
为全面探讨组合预测的类型,以RBF和BP神经网络为基础,建立桥梁变形的非定权组合预测模型。在模型建立过程中,均以单项预测的预测值作为输入信息,以实测值作为输出信息,构建组合预测模型的框架结构。经预测得出非定权组合预测的结果,如表 5所示。
|
|
表 5 非定权组合预测结果统计 Tab. 5 Statistical results of non weighted combination forecasting |
对比单项与非定权组合预测的结果可知,非定权组合预测在对应节点处的相对误差均不同程度地减小,说明非定权组合预测有效地提高了预测精度,达到了期望的目标。其中,RBF神经网络相对误差绝对值的最大值为2.2%,最小值为1.19%;BP神经网络相对误差绝对值的最大值为2.13%,最小值为0.88%。
3) 组合结果对比分析
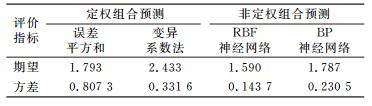
为进一步对比分析各组合预测方法的效果及差异,对各组合方法的相对误差进行作图,见图 4。同时,采用期望和方差指标对各组合方法进行评价,如表 6所示。可见,RBF神经网络在各节点处的相对误差绝对值均较其余组合方法小,说明该方法的组合预测效果相对较优。

|
图 4 组合预测相对误差对比分析 Fig. 4 Comparison analysis of relative errors of combination forecasting |
|
|
表 6 组合预测评价指标统计 Tab. 6 Statistical indicators of combination forecasting |
对比各组合预测的期望指标得出,非定权组合预测的期望值均小于定权组合预测的期望值,说明非定权组合预测的预测精度相对更好;进一步对比方差指标得出,非定权组合预测的方差值均小于定权组合预测的方差值,说明非定权组合预测的结果具有更好的稳定性,综合得出非定权组合预测的结果更优。同时,在定权预测中,误差平方和具有更高的预测精度,但其稳定性不如变异系数法;在非定权组合预测中,RBF神经网络具有更好的预测精度和稳定性,说明非定权组合预测的预测能力具有较好的全面性。综上分析,本文选取RBF神经网络组合预测的结果作为后文误差修正的基础数据,求解桥梁变形的最优预测结果。
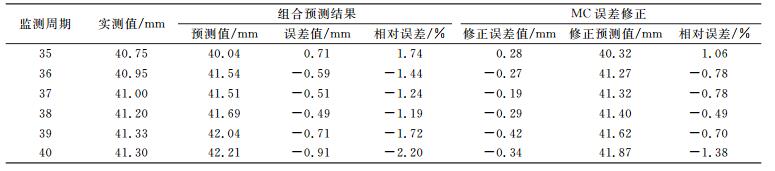
2.4 误差修正预测为进一步提高预测精度,利用MC对最优组合预测结果进行误差修正,结果如表 7所示。通过MC误差修正后,预测结果相对误差的期望值为0.86%,方差值为0.097 3 mm2,预测精度较组合预测的结果有较大提高,稳定性也得到增强,说明本文误差修正模型能有效提高预测精度及稳定性。
|
|
表 7 误差修正结果统计 Tab. 7 Statistics of error correction results |
1) 对比单项预测结果,RBF及BP神经网络的预测效果相对较优,而GM(1, 1)和LS-SVM的预测结果相对较差。这说明前2种方法在本文实例中具有更好的适用性。
2) 非定权组合预测的预测精度及结果的稳定性均优于定权组合预测,说明前者的非线性映射能力更优。
3) 将MC应用到最优组合预测结果的误差修正过程中,修正后相对误差的期望值为0.86%,方差值为0.097 3 mm2,达到期望的预测目标。
| [1] |
胡小伍. Kalman滤波在高铁桥梁变形预测分析中的应用[J]. 测绘地理信息, 2014, 39(5): 58-61 (Hu Xiaowu. Application of Kalman Filtering in High-Speed Railway Bridge Deformation Prediction Analysis[J]. Journal of Geomatics, 2014, 39(5): 58-61)
(  0) 0) |
| [2] |
刘娜, 栾元重, 黄晓阳, 等. 基于时间序列分析的桥梁变形监测预报研究[J]. 测绘科学, 2011, 36(6): 46-48 (Liu Na, Luan Yuanzhong, Huang Xiaoyang, et al. Bridge Deformation Monitoring and Forecasting Based on Time Series Analysis[J]. Science of Surveying and Mapping, 2011, 36(6): 46-48)
(  0) 0) |
| [3] |
张全良, 王克晓, 许国文, 等. 铁路客运专线桥墩沉降趋势预测方法的研究[J]. 铁道建筑, 2012(6): 10-12 (Zhang Quanliang, Wang Kexiao, Xu Guowen, et al. Study on Prediction Method of Settlement Trend of Bridge Pier of Passenger-Dedicated Railway[J]. Railway Engineering, 2012(6): 10-12 DOI:10.3969/j.issn.1003-1995.2012.06.004)
(  0) 0) |
| [4] |
赵栋. 变形预测中的组合预测思想与模型探讨[J]. 华北国土资源, 2014(6): 110-111 (Zhao Dong. Research on Combined Prediction Idea and Model in Deformation Prediction[J]. Huabei Land and Resources, 2014(6): 110-111 DOI:10.3969/j.issn.1672-7487.2014.06.050)
(  0) 0) |
| [5] |
隆然, 董志勇. 基于小波去噪和神经网络的滑坡变形组合预测研究[J]. 路基工程, 2015(6): 33-39 (Long Ran, Dong Zhiyong. Research on Combined Forecast of Landslide Deformation Based on Wavelet De-Noising and Neural Networks[J]. Subgrade Engineering, 2015(6): 33-39)
(  0) 0) |
| [6] |
叶超, 郝付军. 基于支持向量机和BP神经网络的滑坡变形复合式预测[J]. 水土保持通报, 2016(3): 332-337 (Ye Chao, Hao Fujun. Composite Prediction of Landslide Deformation Based on Support Vector Machine and BP Neural Network[J]. Bulletin of Soil and Water Conservation, 2016(3): 332-337)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37