2. 西安测绘信息技术总站,西安市西影路36号,710054
在高精度GNSS网数据处理中,通常采用GAMIT/GLOBK软件[1-4]。但姚宜斌等[5]指出,GLOBK软件假定测站运动呈线性变化,与现实中观测到的测站运动不符,可能会引入粗差。基于此,不少学者开始寻求新的数据处理方法。QOCA软件的开发恰恰满足了这一需求,其在数据处理时顾及测站运动的非线性变化,更加真实地反映了测站的运动规律。王敏等[6]论述了QOCA软件在整体平差方面的优势;占伟等[7]在处理陆态网络连续站数据时采用了QOCA软件;林超才[8]、季海源[9]采用QOCA软件对震区和断裂带进行形变和运动分析,但目前还没有文献具体分析两个软件在数据处理时的差异,更没有对差异进行量化。本文通过实例对两个软件的处理效果进行定量分析与比较,得出一些有益的结论。
1 数据处理策略利用GAMIT/GLOBK和OQCA软件处理陆态网络260个CORS站2011年第100天至2014年第365天观测数据。数据处理可分成4个步骤:
1) 对陆态网络CORS站和周边IGS站进行分区,每个子网中各站点在全国范围大体上均匀分布,共分5个子网,每个子网约60点。其中将我国及周边地区选取的17个IGS站作为公共站,加入每个子网中进行同步处理。
2) 利用GAMIT软件解算各子网单日松弛解,其中的主要参数设置如下:观测值采用无电离层组合LC观测值;天线相位中心改正采用IGS05绝对模型;对流层映射函数采用GMF模型,每1 h估计一个天顶延迟参数;固体潮和极潮模型遵循IERS2004规范,采用BERNE太阳光压模型,采用IGS92地球重力场模型。
3) 利用GLOBK软件将每周的多个子网单日松弛解通过公共站和卫星合并,得到一个包含所有点的周松弛解;对所有的周松弛解进行整体平差估算各测站坐标和速度,或者求取测站的位置时间序列,采取线性拟合的方法求解速度。
4) 利用QOCA软件综合多天的单日松弛解计算测站的位置时间序列,通过分析时间序列获取测站速度。得到每个站点的速度信息之后,进一步推导出相应于该速度场的每周拟合预估坐标,由推估坐标和观测坐标之差的离散程度可以判断出速度场信息的可靠性和每周解坐标的统计精度[3]。
假设测站运动为线性,则测站的位移时间序列可表示为:
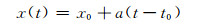
|
(1) |
假设测站运动是线性和周期运动的叠加,也就是QOCA软件的处理模式,测站形变时间序列可表示为:

|
(2) |
式(1)和(2)中,t为GPS周历元,以a为单位;x(t)为预估的GPS周坐标位置;a为估计的每点年线性速度;x0、t0为起始坐标和历元,即整体平差得到的坐标和历元;hi、φi为振幅和相位,最常见的是周年和半年项季节性变化;fj为其余的非线性项。
令v=x(t)-x(t)′,其中x(t)′为每周坐标值真值,由软件计算所得。计算
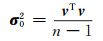
|
(3) |
当残差v呈随机分布时,σ0为每周解坐标的单位权中误差(RMS),反映了每周坐标和速度成果的精度。
2 数据处理结果与分析 2.1 GLOBK处理结果分析在假设测站速度为线性时,有两种获取速度的方法:一是利用GLOBK软件直接平差求得速度场及其精度(方法1);二是针对GLOBK软件解算的位置时间序列进行线性拟合求速度(方法2)。利用时间序列拟合速度的好处一是站与站之间不会互相影响,一个站的非线性运动不会影响其他站的结果;二是可以更加灵活、高效地处理粗差。本文的核心之一在于比较GLOBK和QOCA软件的处理结果差异,因此采用方法1进行计算。
需要说明的是,本次解算的260个CORS站中,有SCLT、GDST、XZSH等20余点位观测数据严重缺失,另有HLAR、LNSY、XIAA等点的垂向位移发生不连续或阶梯性的跳变,很可能是由于天线高的变化或测量错误造成的。为了保证结果的可靠性,将这些测站摒弃,最后得到231个测站的成果。
按方法1得到的每周拟合预估坐标的RMS如图 1所示,测站在E、N、U方向的RMS平均值分别为7.93 mm、7.57 mm和9.93 mm,最大值分别为12.52 mm、12.51 mm和13.99 mm。
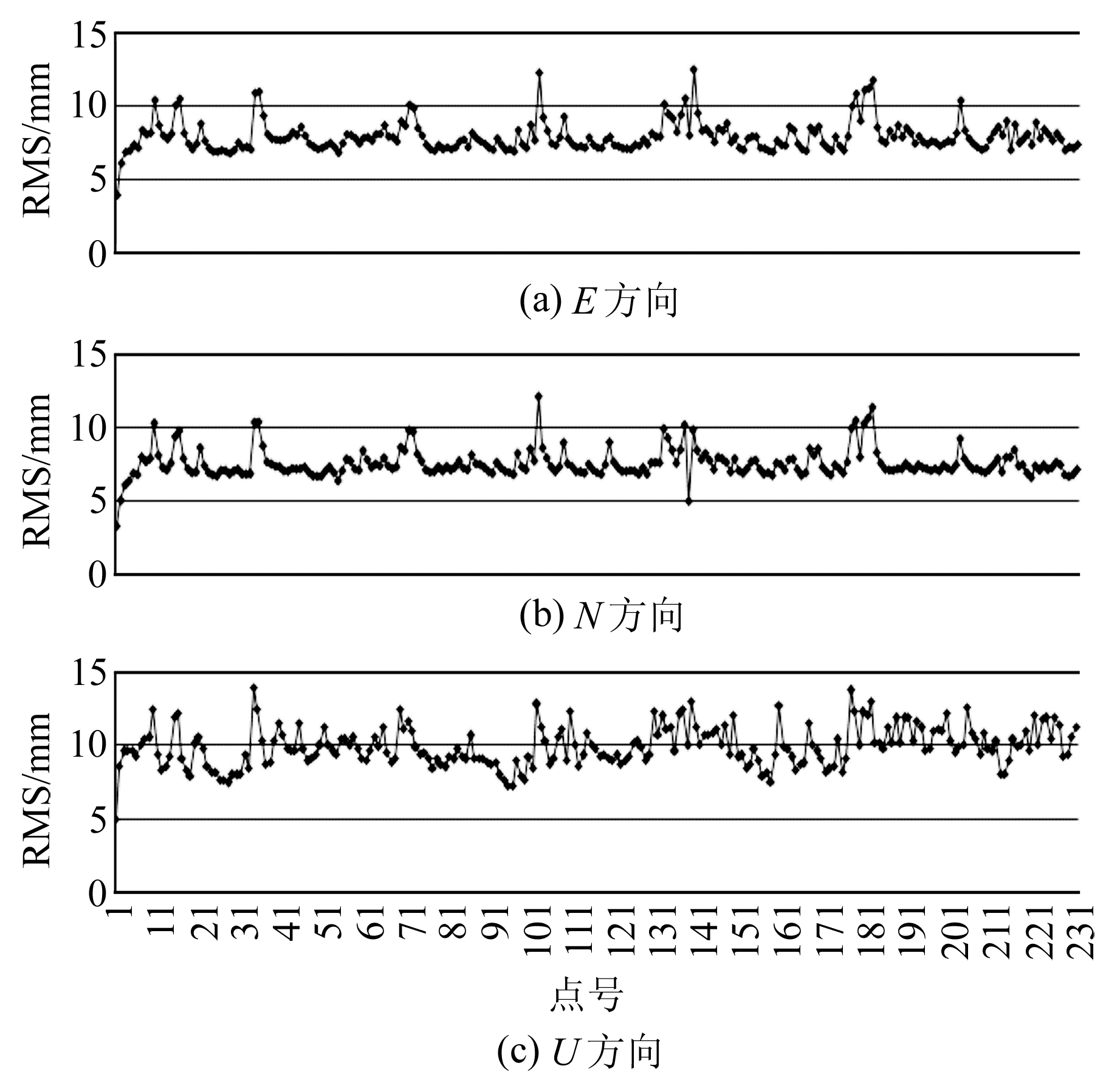
|
图 1 方法1得到的每周拟合预估坐标的RMS Fig. 1 RMS of weekly predicted coordinates of the first method |
根据GLOBK软件解算的周解,利用GMT软件可绘制站点的位置时间序列图,由于篇幅所限,本文仅给出有代表性的QHQL、SCBZ、JIXN、GSMA站的时间序列图(图 2)。从图 2看出,4个站在E方向都呈显著的线性变化,在N和U方向除线性变化外,还有较为明显的周期变化,所以线性速度并不能很好地描述它们的运动趋势。

|
图 2 测站QHQL、SCBZ、JIXN、GSMA的位置时间序列 Fig. 2 Station position time series: QHQL, SCBZ, JIXN and GSMA |
QOCA软件处理流程如下。
1) 计算单天解。利用st_filter模块,将基线解算输出的H文件和SOPAC发布的3个全球解作为输入,得到估计结果文件(包括测站单日解)、残差文件。
2) 分离线性成分。利用analyze_tseri模块对步骤1)得到的位移时间序列进行分析,拟合其中的线性项、周年、半周年项等参数,得到拟合残差。
3) 分离共模误差。利用pca模块对步骤2)的残差坐标序列进行主成分分析,将位移残差序列中共模误差(CME)的主要周期成分和特征向量分离出来,得到主分量文件和本征矢量文件。
4) 时序分析。重复步骤2),不同之处在于需要作区域滤波以剔除共模误差。对剔除共模误差后的位移时间序列中的周年项、半周年项等参数信息进行拟合,最后从位移序列中剔除。QOCA会根据剔除后干净的位移时间序列来拟合一个最终速度,这个速度就是测站相对真实的线性运动速度[9]。
图 3和图 4分别是CORS站AHAQ经过第一次时序分析及进行区域滤波剔除共模误差后的残差序列。可以看出,剔除共模误差后的残差序列比简单的剔除线性项和周期项的残差序列波动更小,说明由共模误差引起的测站位移变化不容忽视。
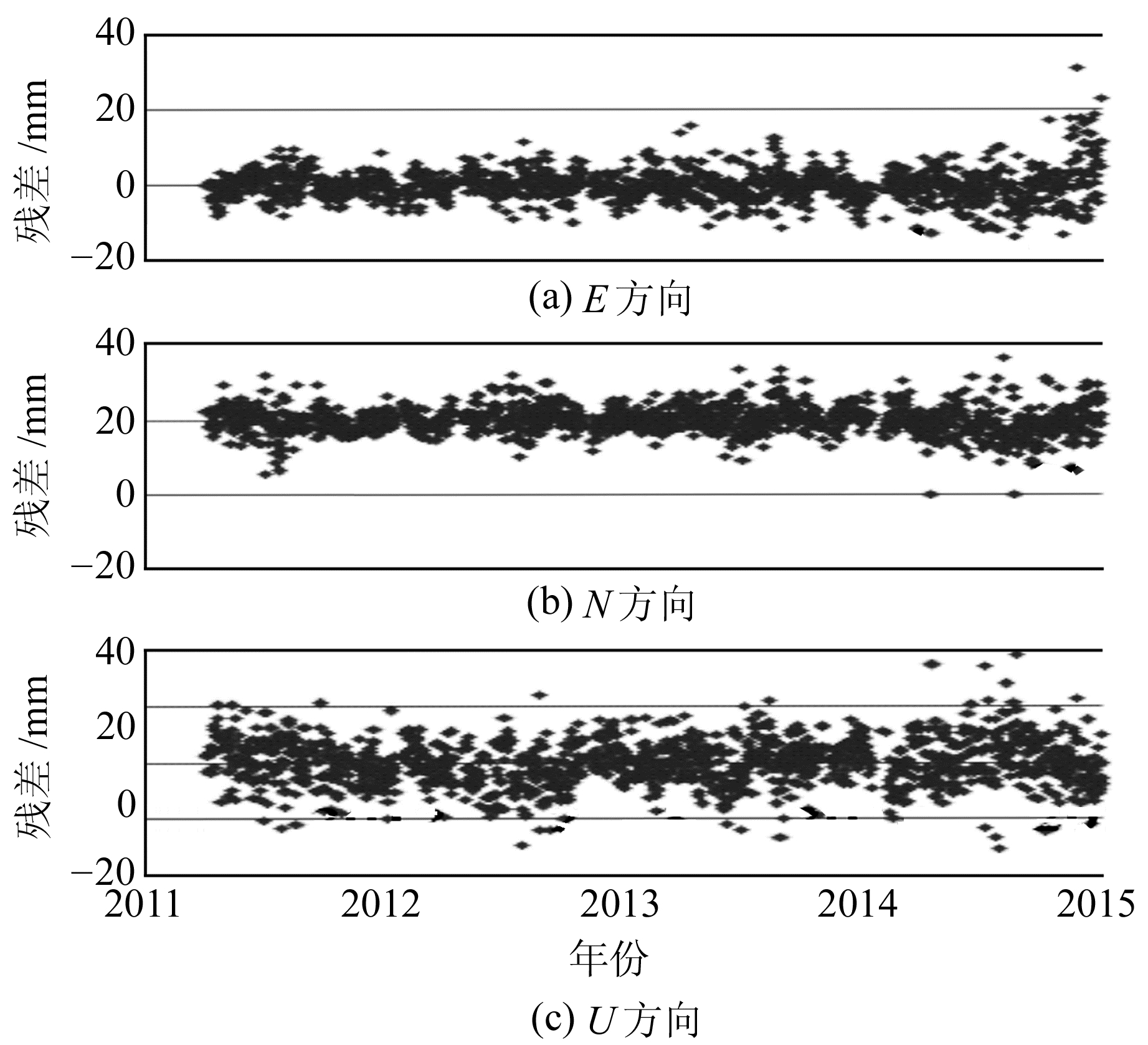
|
图 3 AHAQ站剔除共模误差前残差 Fig. 3 Residuals of AHAQ before deleting CME |
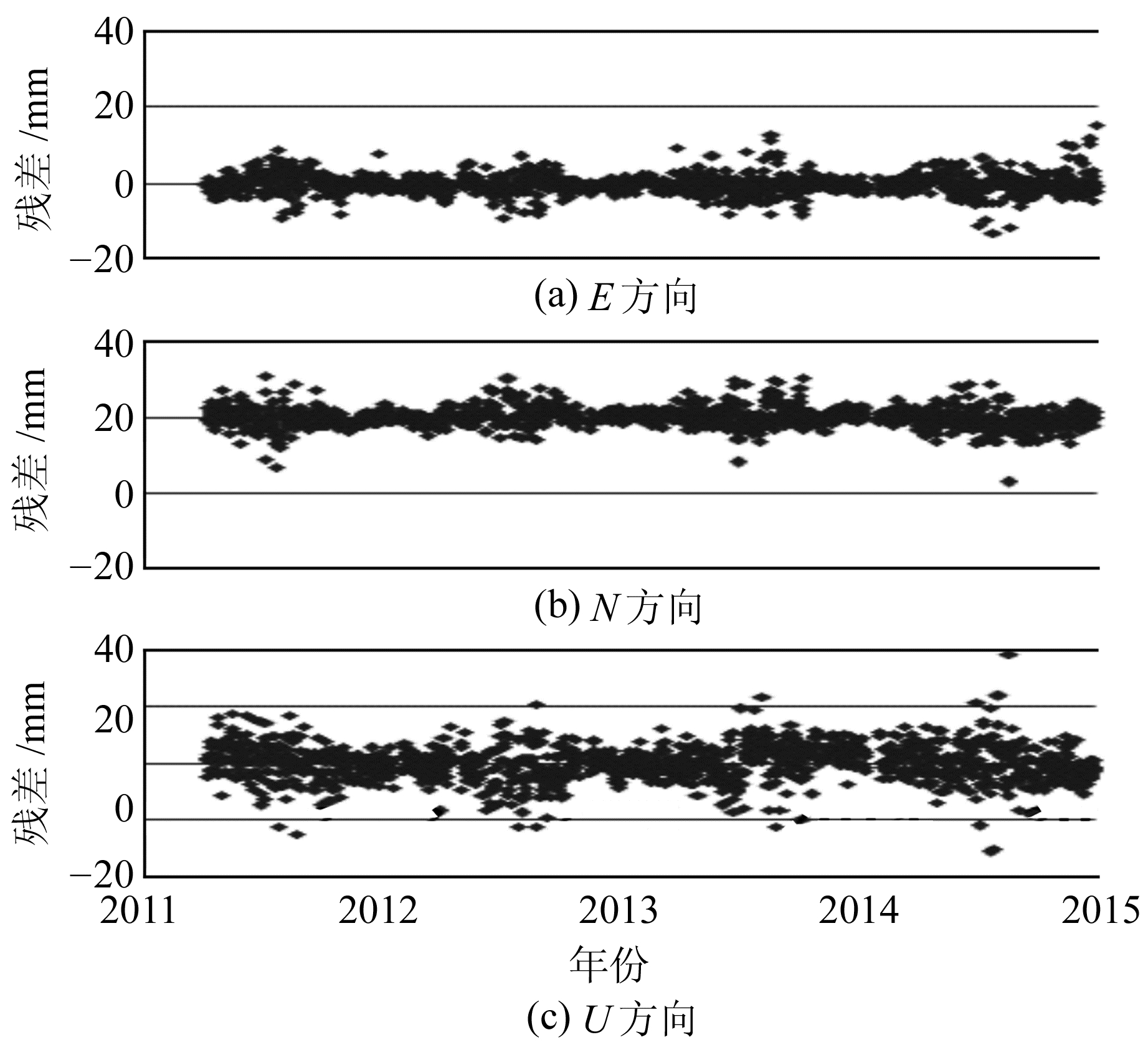
|
图 4 AHAQ站剔除共模误差后残差 Fig. 4 Residuals of AHAQ after deleting CME |
针对剔除共模误差前后的残差序列,按式(3)求RMS,所得结果如图 5所示。剔除共模误差前E、N、U 3个方向的RMS平均值分别为3.6 mm、3.02 mm、6.73 mm,剔除共模误差后RMS平均值分别为2.15 mm、1.52 mm、4.38 mm。可见,共模误差的剔除可使残差序列的RMS在E、N、U 3个方向上分别减小约40%、50%、30%。

|
图 5 剔除共模误差前后残差序列的RMS Fig. 5 RMS of residual series before and after deleting CME |
对比图 1和图 5可以看出,QOCA软件得到的残差序列的RMS较GLOBK软件在E、N、U 3个方向上分别减小70%、80%和70%。两个软件解算的测站线性速度的差值如图 6所示,差值的绝对值平均值在E、N、U 3个方向分别为0.31 mm/a、0.55 mm/a、0.60mm/a,最大值分别为1.31 mm/a、1.62 mm/a、2.24 mm/a,两个软件的解算结果基本吻合。由此可以推测,QOCA软件通过剔除共模误差和拟合周期项提高了解算的精度。

|
图 6 两种软件解算速度值的差值 Fig. 6 The difference between velocities of two software |
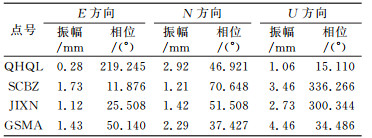
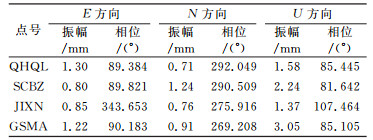
表 1、表 2分别为QOCA软件计算的上述4个站在N、E、U方向位置周年及半周年变化的振幅和初相。将各测站的线性速度、周年和半周年项系数代入式(2)便可计算测站任意历元的坐标,但此时的坐标系是NEU坐标系,实际应用时需要进行NEU坐标系和空间直角坐标系的互相转换。
|
|
表 1 测站位置周年变化的振幅和初相 Tab. 1 Amplitudes and initial phases of annual variations of station positions |
|
|
表 2 测站位置半周年变化的振幅和初相 Tab. 2 Amplitudes and initial phases of semi annual variations of station positions |
本文基于陆态网络CORS站数据对比分析了GLOBK和QOCA两个软件在数据处理时的异同,得出以下结论:
1) 共模误差的剔除可使测站残差序列的RMS在E、N、U方向分别减小约40%、50%、30%。
2) 相比于GLOBK,QOCA软件可通过剔除位移时间序列中的共模误差和拟合周年、半周年项等手段得到更加精确的站点速度,从而使测站的残差序列的RMS在E、N、U方向上分别减小70%、80%和70%。
3) 利用QOCA软件拟合的周年、半周年项系数或者其他周期项的系数进行历元归算是可行的。
| [1] |
唐颖哲, 杨元喜, 宋小勇. 2000国家GPS大地控制网数据处理方法与结果[J]. 大地测量与地球动力学, 2003, 23(3): 77-82 (Tang Yingzhe, Yang Yuanxi, Song Xiaoyong. Adjustment Method and Result of National 2000 GPS Control Network[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 77-82)
(  0) 0) |
| [2] |
魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系:中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410 (Wei Ziqing, Liu Guangming, Wu Fumei. China Geodetic Coordinate System 2000:Velocity Field in Mainland China[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410)
(  0) 0) |
| [3] |
秘金钟, 李毓麟, 张鹏, 等. GPS基准站坐标与速度场精度及随时间变化规律的探讨[J]. 武汉大学学报:信息科学版, 2004, 29(9): 763-782 (Bei Jinzhong, Li Yulin, Zhang Peng, et al. Accuracy of GPS Fiducial Station Coordinate and Velocity Field and Their Time Series[J]. Geomatics and Information Science of Wuhan University, 2004, 29(9): 763-782)
(  0) 0) |
| [4] |
赵庆海, 陈永祥, 朱璇. 基于相似变换法的CGCS2000骨架网精化[J]. 大地测量与地球动力学, 2016, 36(6): 552-555 (Zhao Qinghai, Chen Yongxiang, Zhu Xuan. The Refining of the Skeleton of CGCS2000 Based on Similarity Transformation Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 552-555)
(  0) 0) |
| [5] |
姚宜斌, 施闯. IGS站的非线性变化研究[J]. 武汉大学学报:信息科学版, 2007, 32(5): 424-426 (Yao Yibin, Shi Chuang. On Non-Linear Motion of IGS Station[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 424-426)
(  0) 0) |
| [6] |
王敏, 张祖胜, 许明元, 等. 2000国家GPS大地控制网的数据处理和精度评估[J]. 地球物理学报, 2005, 48(4): 817-823 (Wang Min, Zhang Zusheng, Xu Mingyuan, et al. Data Processing and Accuracy Analysis of National 2000 GPS Geodetic Control Network[J]. Chinese Chinese Journal of Geophysics, 2005, 48(4): 817-823 DOI:10.3321/j.issn:0001-5733.2005.04.013)
(  0) 0) |
| [7] |
占伟, 武艳强, 章力博, 等. 陆态网络GNSS连续站分区解算方案的对比分析[J]. 地震, 2014, 34(4): 137-142 (Zhan Wei, Wu Yanqiang, Zhang Libo, et al. Comparative Analysis of Sub-Network Division Schemes for the GNSS Continuous Stations[J]. Earthquake, 2014, 34(4): 137-142 DOI:10.3969/j.issn.1002-8412.2014.04.023)
(  0) 0) |
| [8] |
林超才.基于GAMIT_GLOBK与QOCA旳汶川震区地壳形变分析与研究[D].成都: 西南交通大学, 2012 (Lin Chaocai. Analysis and Research of Wenchuan Earthquake Zone based on GAMIT/GLOBK and QOCA[D]. Chengdu: Southwest Jiaotong University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10613-1012390848.htm
(  0) 0) |
| [9] |
纪海源.基于GAMIT_GLOBK与QOCA的汾渭断陷带地壳运动研究[D].西安: 西安科技大学, 2014 (Ji Haiyuan. Study of Crustal Movement in Fen-Wei Rift Zone Based on GAMIT/GLOBK and QOCA[D]. Xi'an: Xi'an University of Science and Technology, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10704-1014072719.htm
(  0) 0) |
2. Xi'an Technical Division of Surveying and Mapping, 36 Xiying Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37