2. 东华理工大学测绘工程学院,南昌市广兰大道418号,330013;
3. 武汉大学测绘学院,武汉市珞喻路129号,430079
在许多情况下,系数矩阵同样由观测量组成,而这些观测量是通过测量手段获取的,就不可避免地存在误差,即系数矩阵也含有误差。当系数矩阵和观测向量同时含有误差时,应建立EIV模型,采用总体最小二乘求解。近年来,已有大量关于总体最小二乘的研究,其理论日趋成熟,成为测绘数据处理领域研究的热点问题。文献[1-2]对加权总体最小二乘算法进行研究,文献[3-4]推导病态总体最小二乘算法,文献[5-6]研究附加约束条件的总体最小二乘,以及文献[7]研究多元总体最小二乘问题。以上研究都认为各观测量的精度是相同的,然而在测绘数据处理领域中,如GPS网、三角网和导线网,经常含有不同类型或不同精度的观测量。平差计算时,一般根据先验方差进行定权,但是先验方差并不能精确已知,此时确定的各类观测值的权不够准确,需要采用验后方差分量估计的方法进行二次定权。验后方差分量估计(VCE)方法主要包括赫尔默特估计(Helmert)、最小范数二次无偏估计(MINQUE)、最优不变二次无偏估计(BIQUE)及VCE的扩展研究等。针对总体最小二乘中含有不同精度的观测量,文献[8-9]将总体最小二乘问题和VCE进行综合研究,分别采用LS-VCE和MINQUE-VCE对总体最小二乘问题中观测向量和系数矩阵中元素的方差分量进行求解,从而得到更准确的参数估计值;文献[10-11]将Helmert方差分量估计用于总体最小二乘中,同样对观测向量和系数矩阵中元素的方差分量进行求解。
另外,观测量中通常不可避免地含有粗差,如何对粗差进行探测和定位,消除其对平差结果的影响,是提高平差结果精度的一个关键问题。基于最小二乘理论,周江文[12]提出IGG权函数,杨元喜[13]进行了扩充,提出IGGⅡ权函数。已有许多学者将稳健估计理论与总体最小二乘结合,陈义、陆珏[14]以三维坐标转换为例,阐述一种稳健总体最小二乘方法,实际是将Huber权函数用于Gauss-Helmert加权总体最小二乘;龚循强、李志林[15]进行改进,提出基于IGG权函数的稳健总体最小二乘,并与文献[14]提出的方法作详细的比较分析,得出IGG权函数的稳健总体最小二乘计算结果更为可靠;文献[16-17]引入标准化残差和中位数来提高稳健总体最小二乘的抗差性能。
总体最小二乘方差分量估计并不具有稳健性,当观测数据中含有粗差时,其计算结果往往面目全非,得不到准确的参数估值。因此,本文在进行总体最小二乘方差分量估计前,先根据稳健估计的原理选取合适的权函数,分别构建系数矩阵和观测向量的等价权,再以构建的等价权作为初始权,按照总体最小二乘Helmert方差分量估计进行计算。为了方便直接引用Helmert方差分量估计,本文从最小二乘配置的角度,根据广义最小二乘原理,将总体最小二乘转换为最小二乘的形式求解。
1 加权总体最小二乘算法总体最小二乘函数模型如下[1]:

|
(1) |
式中,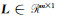
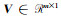

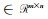
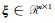
采用高斯-牛顿法将非线性模型(1)转化为线性模型,迭代求解。设第j次迭代后的估值为ξ(j),则参数ξ表示为:
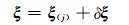
|
(2) |
将式(2)代入式(1)中,为了避免迭代发散或收敛错误,采用EA的第j次迭代值EA(j)代替EA计算系数矩阵,记A(j)=A+EA(j),得:
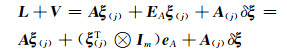
|
(3) |
式中,eA=vec(EA),vec(·)表示将矩阵按列拉直变换。
考虑到系数矩阵中可能同时含有无误差的常数项和随机元素,并且不同的位置有相同的元素存在,为了保证常数项的改正数为0,不同位置的相同元素改正数相同,将系数矩阵中的随机元素提取出。假设系数矩阵中含有u个不同的随机元素,则可以组成u×1的列向量a,用ea表示随机元素a的误差改正数,则有eA=Mea,M是由常数构成的a的系数矩阵,为mn×u矩阵,可通过求矩阵vec(A)对随机元素a的雅可比矩阵获得。
代入式(3)得:
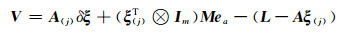
|
(4) |
可以看出,式(4)为最小二乘配置的标准形式,将δξ看作不考虑随机信息的倾向参数,ea看作考虑随机信息的信号参数。根据广义最小二乘原理,将ea的期望作为虚拟观测值,而ea的期望为0,则可以得到:
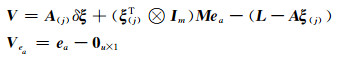
|
(5) |
将总体最小二乘转换为最小二乘求解,整理得:
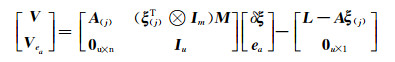
|
(6) |
此时总体最小二乘目标函数为VTPLV+VeaTPaVea=min,PL为观测向量L的权阵,Pa为随机元素a的权阵,令
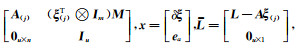
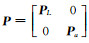
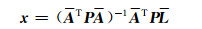
|
(7) |
通过迭代计算,直到满足收敛条件为止。
2 稳健总体最小二乘Helmert方差分量估计 2.1 总体最小二乘的Helmert方差分量估计本文从最小二乘配置的角度,根据广义最小二乘原理将总体最小二乘转换为最小二乘形式,进而可以直接引用Helmert方差分量估计。
令
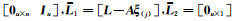
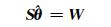
|
(8) |
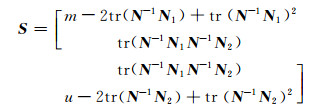
|
(9) |
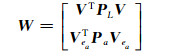
|
(10) |
式中,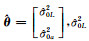
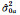
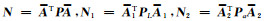
通过对式(9)求解,可以得到观测向量和系数矩阵中随机元素的方差分量估值:
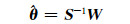
|
(11) |
总体最小二乘多余观测数r与最小二乘多余观测数是一样的:r=(m+u)-(n+u)=m-n,但总体最小二乘多余观测数在观测向量和系数矩阵的随机元素之间进行分配,即r=rL+ra。这里可以直接得出观测向量和系数矩阵中随机元素的多余观测数为:
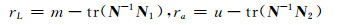
|
(12) |
则观测向量和系数矩阵中随机元素的方差分量估值可简化为:
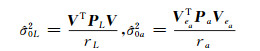
|
(13) |
总结Helmert方差分量估计的计算步骤如下:
1) 按最小二乘求参数初值ξ(0)=(ATPLA)-1ATPLL,EA0=0;
2) 进行第一次总体最小二乘平差计算,求得V和Vea,并计算VTPLV和VeaTPaVea;
3) 按式(13)进行方差分量估计,求得观测向量和系数矩阵中随机元素的方差分量估值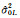


|
(14) |
式中,c为任意常数,一般选
4) 重复步骤2)、3),直至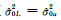
为了使总体最小二乘方差分量估计具有稳健性,本文继续引入稳健估计理论,在总体最小二乘方差分量估计前先进行稳健估计。已有大量文献证明,IGG权函数更适于测量计算。IGG权函数为[13]:
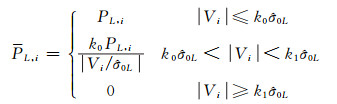
|
(15) |

|
(16) |
式中,PL, i为观测向量的等价权PL的第i个对角线元素,Pa, i为随机元素a的等价权Pa的第i个对角线元素;PL, i为PL的第i个对角线元素,Pa, i为Pa的第i个对角线元素;Vi为V的第i个元素,Vea, i为Vea的第i个元素;k0、k1为常数(一般取k0=1.5, k1=2.5)。
本文提出的稳健总体最小二乘Helmert方差分量估计分为两步来计算:第一步是按照总体最小二乘计算残差V和Vea,按式(13)计算观测向量和系数矩阵中随机元素的单位权中误差估值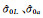
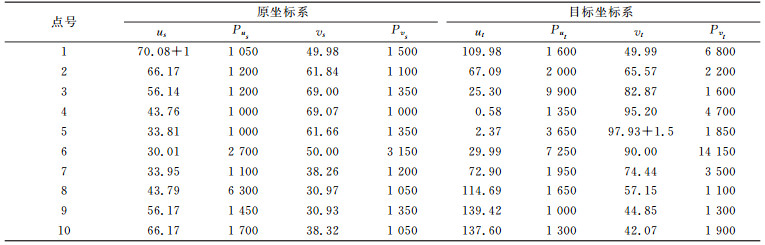
以六参数平面坐标转换为例,采用文献[14]中的数据,并在us1上加入大小为1的粗差,在vt5上加入大小为1.5的粗差。数据如表 1所示,(us, vs)表示原坐标系的坐标,(ut, vt)表示目标坐标系的坐标,参数真值
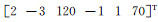
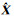

|
|
表 1 坐标观测值及其相应的权 Tab. 1 Coordinate observations and their corresponding weights |
|
|
表 2 不同的算法 Tab. 2 The different algorithm |
|
|
表 3 不同方案的参数估计结果 Tab. 3 The results of estimated parameters by different method |

|
图 1 方案4的两个方差分量估值 Fig. 1 Estimation value of two variance factor by method 4 |
|
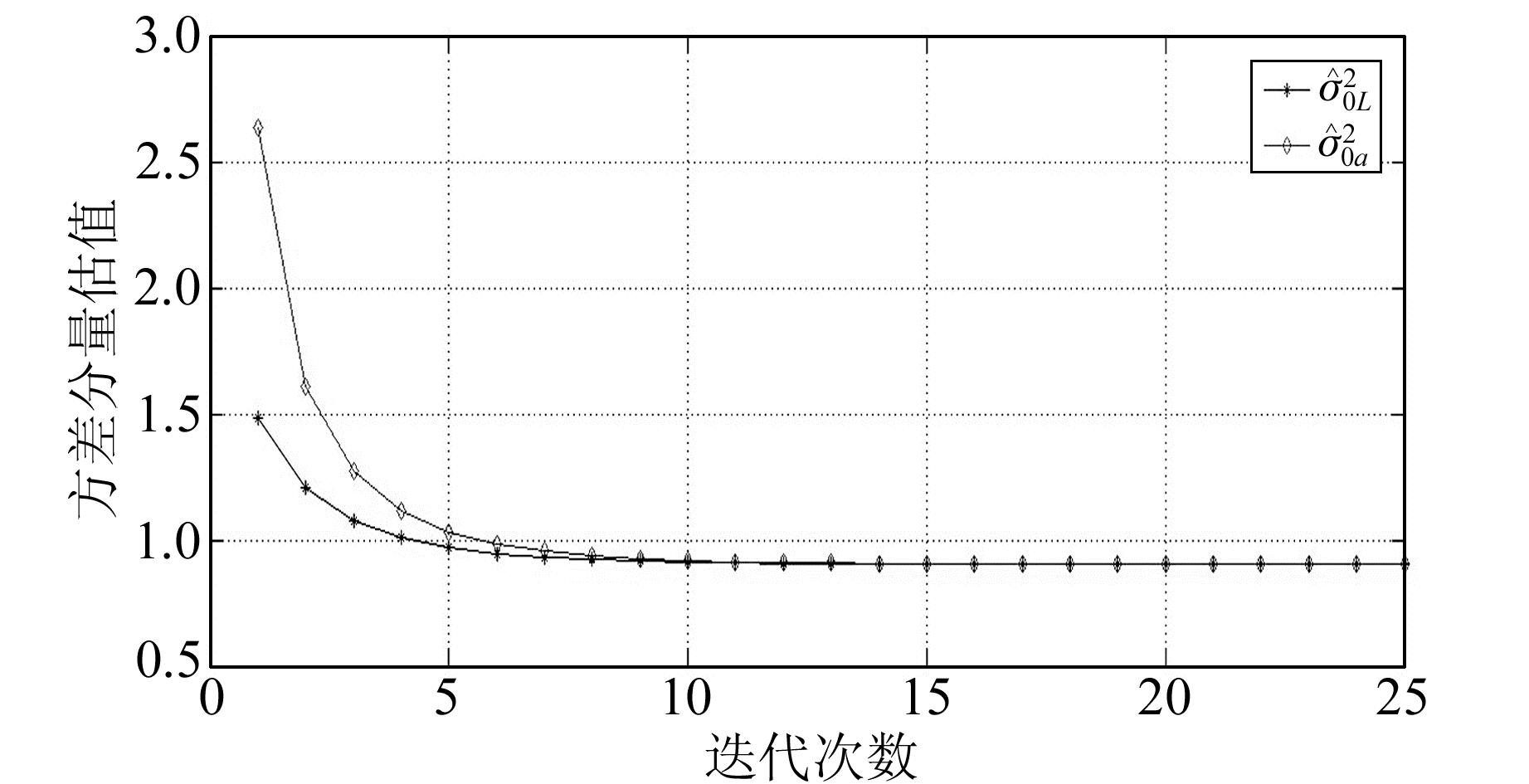
图 2 方案6的两个方差分量估值 Fig. 2 Estimation value of two variance factor by method 6 |
1) 从表 3的计算结果可以看出,方案2与方案1的计算结果基本相同,方案4与方案3的计算结果基本相同,说明本文的加权总体最小二乘算法和总体最小二乘Helmert方差分量估计均是切实可行的。加权总体最小二乘认为观测向量和系数矩阵所对应的单位权方差是相同的,然而实际上表 1中原坐标系坐标观测值与目标坐标系坐标观测值的精度并不相同,导致观测向量和系数矩阵分别对应不同的单位权方差,此时采用加权总体最小二乘算法显然是不合理的,需要通过验后估计的方法进行二次定权。本文的总体最小二乘Helmert方差分量估计将原坐标系坐标观测值与目标坐标系坐标观测值看作具有不同的单位权方差分量,通过方差分量改变权值,最终达到方差分量一致,因此参数的计算结果得到了进一步的改正,与真值最为接近。
2) 从方案5的计算结果可以看出,其参数估值与真值差异较大,这是因为总体最小二乘Helmert方差分量估计不具有抵抗粗差的能力。方案6的计算结果与真值接近,因为方案6通过先构建等价权,再进行方差分量估计,使得算法具有了稳健性,说明本文的稳健总体最小二乘Helmert方差分量估计是可行的,在观测数据中含有粗差的情况下,可以很好地消除粗差的影响,提高方差分量估计计算结果的可靠性。
4 结语本文从最小二乘配置的角度,根据广义最小二乘原理将总体最小二乘转换为最小二乘求解,从而可以引用Helmert方差分量估计的原理,处理不同精度或者不同类型的观测量数据,得到更可靠的计算结果。同时还考虑到观测数据中可能含有粗差的情况,提出稳健总体最小二乘Helmert方差分量估计,使得总体最小二乘方差分量估计具有稳健性。
| [1] |
Amiri-Simkooei A, Jazaeri S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodesy, 2012, 2(2): 113-124
(  0) 0) |
| [2] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustmentin Partial Errors-in-Variables:Algorithm and Statisitical Analysis[J]. J Geod, 2012, 86: 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [3] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [4] |
顾勇为, 归庆明, 赵俊. 病态加权总体最小二乘靶向病灶的正则化方法[J]. 大地测量与地球定力学, 2016, 36(3): 253-256 (Gu Yongwei, Gui Qinming, Zhao Jun. Target Focus Regularization as Compared with Ill-Posed Weighted Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 253-256)
(  0) 0) |
| [5] |
曾文献, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1 013-1 018 (Zeng Wenxian, Fang Xing, Liu Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1 013-1 018)
(  0) 0) |
| [6] |
Fang X. On Non-Combinatorial Weighted Total Least Squares with Inequality Constraints[J]. Journal of Geodesy, 2014, 88(8): 805-816 DOI:10.1007/s00190-014-0723-y
(  0) 0) |
| [7] |
王乐洋, 赵英文, 陈晓勇, 等. 多元总体最小二乘问题的牛顿解法[J]. 测绘学报, 2016, 45(4): 411-417 (Wang Leyang, Zhao Yingwen, Chen Xiaoyong, et al. A Newton Algorithm for Multivariate Total Least Squares Problems[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 411-417)
(  0) 0) |
| [8] |
Amiri-Simkooei A R. Application of Least Squares Variance Component Estimation to Error-in-Variables Model[J]. Journal of Geodesy, 2013, 87(10-12): 935-944 DOI:10.1007/s00190-013-0658-8
(  0) 0) |
| [9] |
Xu P, Liu J. Variance Components in Error-in-Variables Model:Estimability, Stability and Bias Analysis[J]. Journal of Geodesy, 2014, 88(8): 719-734 DOI:10.1007/s00190-014-0717-9
(  0) 0) |
| [10] |
王乐洋, 许光煜. 加权总体最小二乘平差随机模型的验后估计[J]. 武汉大学学报:信息科学版, 2016, 41(2): 254-261 (Wang Leyang, Xu Guangyu. Application of Posterior Estimation of a Stochastic Model on the Weighted Total Least Squares Problem[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 254-261)
(  0) 0) |
| [11] |
Wang L Y, Xu G Y. Variance Component Estimation for Partial Errors-in-Variables Model[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35-55 DOI:10.1007/s11200-014-0975-2
(  0) 0) |
| [12] |
周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120 (Zhou Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographic Sinica, 1989, 18(2): 115-120 DOI:10.3321/j.issn:1001-1595.1989.02.005)
(  0) 0) |
| [13] |
杨元喜. 等价权原理-参数平差模型的抗差最小二乘[J]. 测绘通报, 1994, 49(6): 33-35 (Yang Yuanxi. The Principle of Equivalent Weight the Robust Least Squares Solution of Uniformity Model of the Parameter Adjustmen[J]. Bulletin of Suiveying and Mapping, 1994, 49(6): 33-35)
(  0) 0) |
| [14] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722 (Chen Yi, Lu Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722)
(  0) 0) |
| [15] |
龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888-894 (Gong Xunqiang, Li Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888-894)
(  0) 0) |
| [16] |
陶叶青, 高井祥, 姚一飞. 基于中位数法的抗差总体最小二乘估计[J]. 测绘学报, 2016, 45(3): 297-301 (Tao Yeqing, Gao Jingxiang, Yao Yifei. Solution for Robust Total Least Squares Estimation Based on Median[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 297-301)
(  0) 0) |
| [17] |
王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6): 602-608 (Wang Bin, Li Jiancheng, Gao Jingxiang, et al. Newton-Gauss Algorithm of Robust Weighted Total Least Squares Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 602-608)
(  0) 0) |
2. Faculty of Geomatic, East China Institute of Technology, 418 Guanglan Road, Nanchang 330013, China;
3. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37