2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
目前,基于GNSS的动态载体精密姿态测量技术得到广泛应用。由于动态载体姿态测量要求的观测历元较少(大多为单历元), 存在模型误差大、观测信息不足的问题[1],在观测数据质量较差的情况下, 仅采用GNSS观测数据不容易快速固定模糊度。在姿态测量过程中, 接收机之间的相对位置一般可以事先测量, 国内外学者通过附加一些约束条件来辅助基线解算中模糊度的快速固定, 特别是基线长约束条件[2-5]。
传统的方法多是将基线长约束方程线性化作为观测方程进行模糊度固定, 或者将基线长度作为一个判定条件对模糊度候选组进行确认, 通过提高浮点解的精度, 或者严格控制模糊度候选值的范围来提高模糊度固定成功率[3-4]。文献[5]推导了基线长约束线性化的余项对模糊度浮点解的影响, 给出了基线长线性化的适用范围。实际应用中, 由于载体平台大小的限制, GNSS基线长度布设一般较短(少于20 m), 基线长约束线性化余项对模糊度浮点解的影响较大, 一般不将基线长约束条件直接线性化。而且单纯采用基线长度作为诊断条件并不严密, 存在模糊度搜索效率较低、错选候选值的情况[6]。Teunissen等[7-8]利用事先已知的几何约束条件, 对最小二乘模糊度降相关(LAMBDA)算法进行改进, 提出Constrained LAMBDA(CLAMBDA)算法。该算法利用几何约束条件可以一定程度上提高模糊度固定的成功率, 但当模糊度向量维数较多, 如多系统或者多基线数据同时处理时, 模糊度搜索的效率迅速降低, 部分历元甚至存在模糊度不能固定的情况。
针对以上问题,本文首先探讨了利用基线长约束提高模糊度固定成功率的基本原理及附有基线长约束的CLAMBDA算法的具体实现过程;然后基于部分模糊度搜索策略提出了改进的CLAMBDA算法,先通过固定宽巷模糊度,缩小椭球的搜索空间,再利用模糊度协因数矩阵选择合适的观测值,降低模糊度候选组维数,提高模糊度的搜索效率;最后通过静态和动态的实测数据对该方法的有效性进行验证分析。
1 数学模型及解算 1.1 CLAMBDA搜索算法基本原理GPS双差数学模型[9]为:
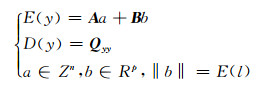
|
(1) |
式中,y为双差观测值,A和B分别对应模糊度参数a和基线分量b的系数矩阵,l为基线长度,此时基线长约束可以定义为一个多维球面Sl。式(1)对应的最小二乘极值问题可写为:
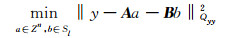
|
(2) |
该式是一个二次型约束的整数最小二乘极值问题(quadratically constrained integer least-squares,QC-ILS)。将式(2)进行正交分解可化为:
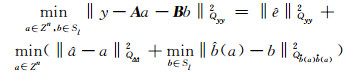
|
(3) |
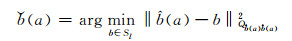
|
(4) |
若不考虑约束条件和模糊度的整数特性,直接利用最小二乘求解可以得出参数的浮点解及其协因数阵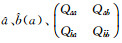
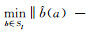
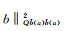

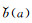
|
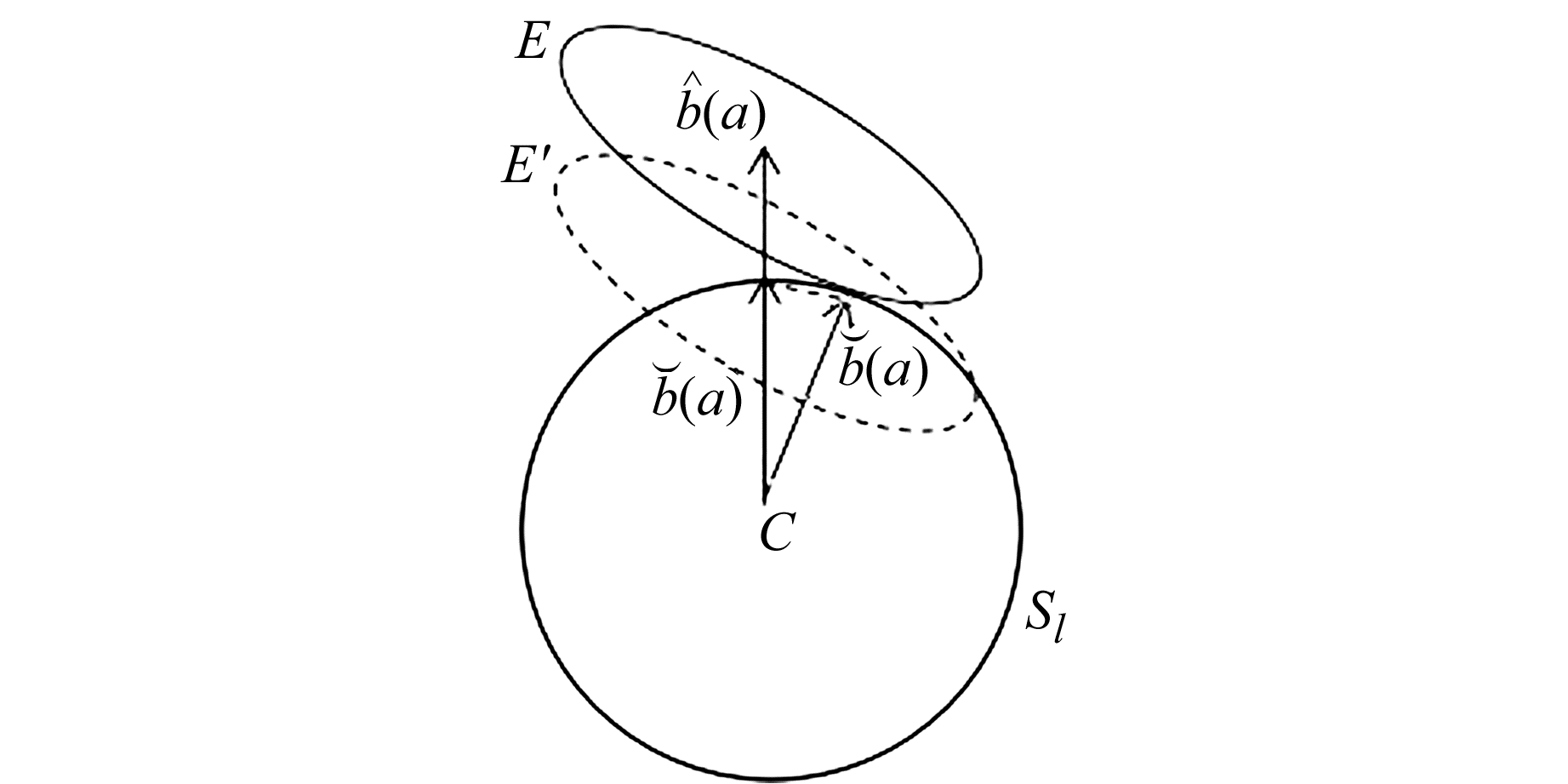
图 1 模糊度浮点解和固定解的几何关系 Fig. 1 The geometric relationship between the float and fixed ambifuity |
将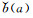

|
(5) |
由此可以将模糊度搜索的目标函数表示为:
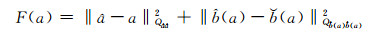
|
(6) |
与普通的模糊度搜索目标函数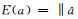
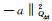
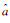
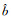
实际应用中,基线分量长度也是事先测量的。用σl表示基线长的测量精度,则F(a)可以改写为:
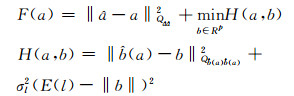
|
(7) |
采用高斯牛顿迭代法或者一些搜索算法可以求解式(7)中非线性最小二乘问题。为简化复杂问题,假设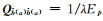
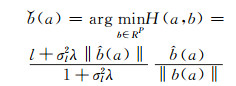
|
(8) |
利用Frobenius范数的性质,可以求出拉格朗日乘数因子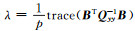
由于附加约束后模糊度搜索空间不再是椭球型,不方便模糊度的搜索,CLAMBDA算法一般通过一个更大的椭球型搜索空间去搜寻该空间内的模糊度候选值。
1.2 改进的CLAMBDA算法在GNSS动态相对定位中,搜索椭球的大小对算法的搜索效率影响很大。例如,当卫星高度角比较低时受多路径和噪声影响,或观测值发生周跳,搜索椭球半径往往过大,模糊度很难固定[12]。实际的模糊度向量中,仅有3个是独立的,确定3个模糊度后,其他都可通过确定的线性关系确定,这是部分模糊度搜索的依据。部分模糊度搜索策略的核心思想是依据一定的准则从模糊度全集中选出质量较好的部分模糊度子集进行固定,可以提高模糊度固定的成功率和搜索效率。CLAMBDA算法中每一次对模糊度候选组进行判断都需要重复搜索椭球内的模糊度候选值,算法的复杂度较高,且搜索椭球易受不良观测值影响[13]。
为避免由于部分观测数据质量较差时CLAMBDA算法为搜寻正确模糊度向量过度扩张搜索半径,影响模糊度搜索的效率和成功率,本文根据部分模糊度搜索的思想,提出了一种改进的CLAMBDA算法,其原理如下。
1) 搜索和固定宽巷模糊度
利用伪距观测和宽巷(超宽巷)载波相位观测进行模糊度固定和解算,由于噪声波长与其组合波长的比值很小,宽巷模糊度单历元固定的成功率非常高。将固定的宽巷模糊度的观测方程代替原来的码观测方程,可以解算出精度更高的浮点解,有效地缩小搜索椭球。若无法固定宽巷模糊度,则依旧采用码观测方程。
2) L1/L2/L5波段模糊度搜索策略
① 计算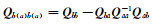
② 采用标准LAMBDA算法计算模糊度候选组aILS,并采用ratio检验判断是否通过,若通过检验则直接输出模糊度候选值;若未通过检验,则进行下一步;
③ 将模糊度候选组按照协方差矩阵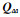
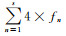
④ 采用CLAMBDA算法快速计算模糊度候选组aILS。
CLAMBDA算法解算模糊度的成功率较高,但该算法无法像传统的LAMBDA算法一样通过计算模糊度候选组ratio值判断模糊度是否固定。实际验证时,一般将其解算结果与未发生周跳情况下多个历元解算的模糊度值或已经通过检验的模糊度值进行比较,判断其是否固定正确。
2 算法性能测试与精度评估为测试CLAMBDA算法以及新方案的性能,设计3种解算方案进行对比,并分别用静态和动态的实验进行验证分析:方案1为LAMBDA方法,方案2为CLAMBDA算法,方案3为改进的CLAMBDA算法。实验中的电脑配置为:CPU型号为Intel酷睿i5 6500,CPU主频为3.2 GHz,内存为4 G,软件平台为MATLAB2013版。
实验1:采用2015-08-29实测的两条长约2 m的超短基线的静态观测数据,分别用A1和B1表示,采样率为1 s,共3 600个历元。采用GPS单历元双频观测数据进行测试,卫星截止高度角设为10°。
实验2:采用澳大利亚科廷大学短基线IGS站(CUT0, CUTA, CUTB)的静态实验数据,分别用A2和B2表示,数据采样间隔设为30 s,卫星截止高度角设为10°, 共2 800个历元。采用GPS和BDS双系统的单历元双频观测数据进行测试,卫星截止高度角设为10°。
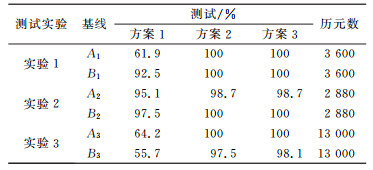
实验3:采用2015-08-29实测的两条短基线的观测数据,分别用A3和B3表示,采样率为1 s,共13 000个历元,观测一段时间后将基线绕某一固定轴线缓慢旋转,采用GPS单历元双频观测数据进行测试,卫星截止高度角设为10°。将整周模糊度固定成功率定义为模糊度固定成功的历元数与总历元数的比值,统计3种方案的模糊度固定成功率(表 1)。事先对观测数据进行周跳探测和修复,将多个历元解算的已经通过检验的模糊度值作为模糊度参考值。
|
|
表 1 3种方案的模糊度解算成功率 Tab. 1 Success rate of ambiguity resolution using three schemes |
分析3种方案在3个实验中的模糊度固定成功率的情况可以看出,不论是静态实验还是动态实验,方案2和方案3的成功率都高于普通的LAMBDA算法。特别是动态实验情况下(见实验3),普通的LAMBDA算法成功率只有55.7%,可能原因是测距码和相位的噪声相对于静态都比较大,而CLAMBDA算法和部分CLAMBDA解算方案都超过95%,说明后两种方案都可以合理利用基线长约束条件去搜索合适的模糊度。
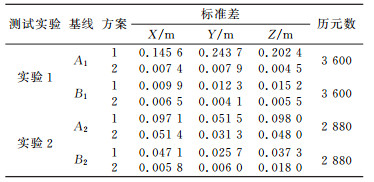
由于方案2和方案3模糊度固定的成功率很接近,而模糊度固定后,两种方案的精度一致,本文比较分析了CLAMBDA算法和LAMBDA算法在静态实验条件下的精度情况(表 2)。图 2、图 3分别为方案1和方案2在静态、动态实验中最后解算的水平基线分量。
|
|
表 2 CLAMBDA算法和LAMBDA算法的解算精度 Tab. 2 Calculation accuracy of CLAMBDA method and LAMBDA method |
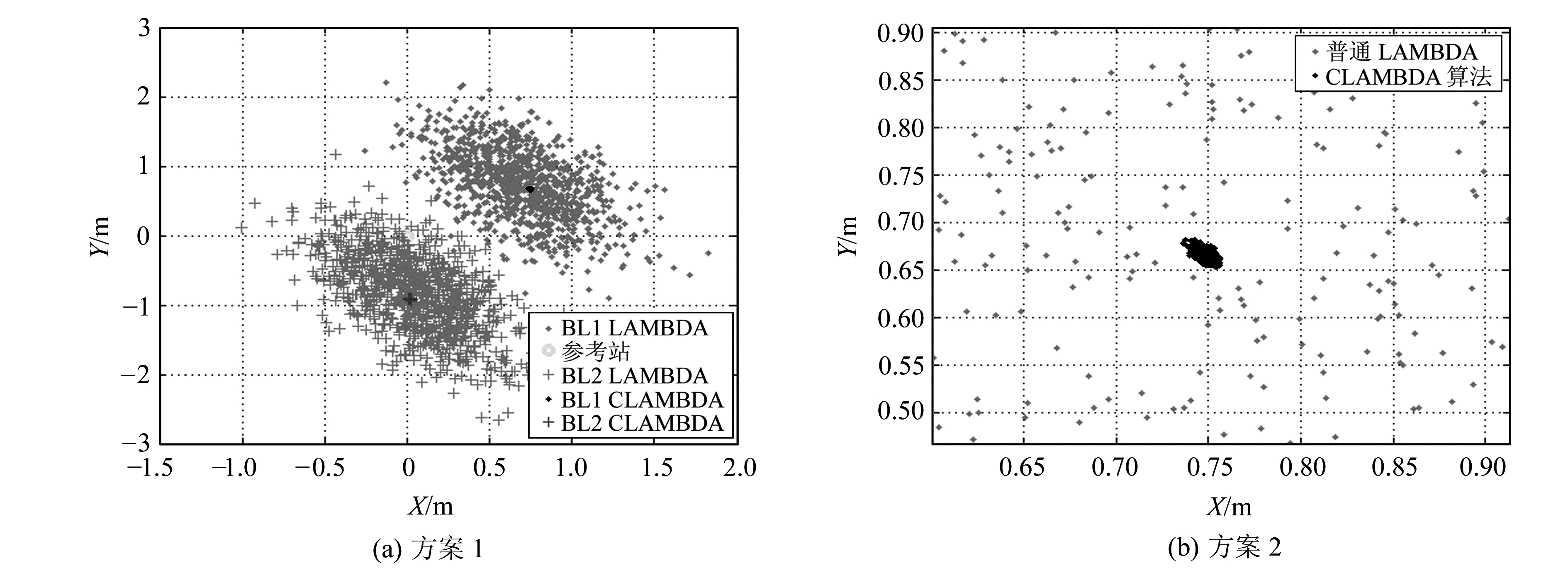
|
图 2 静态基线解算结果比较 Fig. 2 The result comparison of static base line solution |

|
图 3 动态基线解算轨迹比较 Fig. 3 The result comparison of static base line solution |
结合表 2和图 2、图 3可以看出,在静态和动态情况下,普通LAMBDA算法在部分观测历元时很难固定模糊度,只能用实数解代替;而CLAMBDA算法通过基线长约束可以明显提高基线解算的精度。本文对LAMBDA算法和CLAMBDA算法存在部分历元难以固定模糊度的情况进行了具体分析,发现此时的观测卫星数明显较少(一般少于5颗),并且此时由模糊度精度因子ADOP (ambiguity dilution of precision)计算出的先验模糊度成功率一般不高,说明观测卫星数较少时,CLAMBDA算法的搜索成功率也会降低。
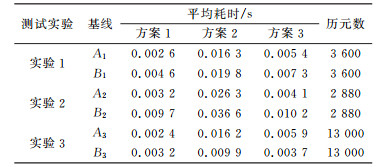
本文对3种方案的解算效率进行统计(表 3)可以看出,3种方案中方案1的搜索效率要比后两种方案高,搜索时间均小于0.01 s,这是因为后两种方案在搜索过程中都需要不断地扩大椭球半径,调用搜索函数计算候选值的代价函数,算法的复杂度较高;方案2的平均搜索时间最多,而方案3较方案2的平均搜索时间要少得多,在量级上接近普通LAMBDA算法的搜索时间,较原方案搜索效率提高了近3倍。说明改进的CLAMBDA算法通过选择合理的观测信息,降低了模糊度的维数,提高了模糊度搜索的效率。
|
|
表 3 3种方案耗时统计 Tab. 3 The statistics of searching time of ambiguity using three schemes |
采用实验2的A基线数据,并且使用GPS+GLONASS+BDS 3种系统共7个频率,模糊度矩阵维数达到50维以上,统计了方案2和方案3单历元耗时情况(图 4)。由图可见,方案3计算耗时较方案2明显降低,模糊度的搜索效率提高了近3倍。
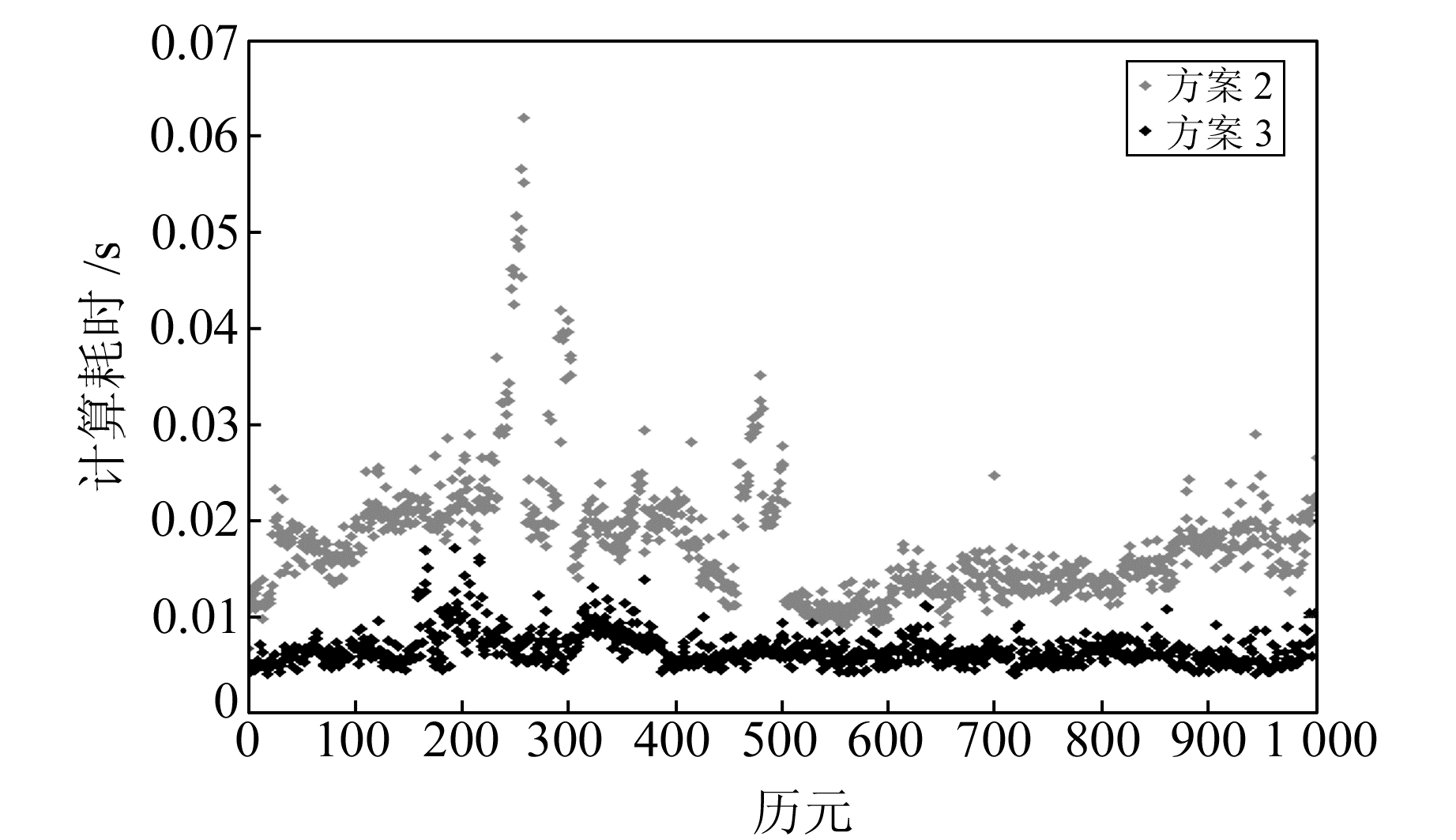
|
图 4 方案2和方案3模糊度搜索耗时结果比较 Fig. 4 Comparison of two methods for searching time |
综合分析3种方案可以得出结论:CLAMBDA算法及其改进的CLAMBDA算法都可以明显提高模糊度固定的成功率,大大提高基线解算的精度。由于部分模糊度搜索方案通过选择合理的相位观测值,降低模糊度个数,提高了解算的效率,更有利于实时姿态测量。实际姿态测量中,一般采用多条基线组成的接收机阵进行姿态测量,约束条件变成基线长和接收机间相对位置(角度),此时的模糊度维数很高,搜索效率会更低;而部分模糊度搜索方案可以有效提高模糊度搜索效率。
3 结语CLAMBDA算法可以充分利用先验基线长信息,提高基线解算的成功率,但其在模糊度搜索效率方面还有一些不足。本文主要讨论了附有基线长约束的CLAMBDA算法的基本原理及实现方法,针对其处理多维数据时搜索效率较低的问题提出了一种改进的CLAMBDA搜索算法。新算法首先固定宽巷模糊度,初步缩小搜索椭球空间,并利用部分模糊度搜索原理,通过剔除不合理观测值,降低模糊度的维数。该方法改善了搜索空间形状,在保证模糊度搜索成功率的情况下,提高了模糊度搜索的效率。
在GNSS姿态测量中,接收机之间的基线长度和相对位置一般可知,这部分先验信息可以有效地应用于GNSS模糊度搜索算法中,提高模糊度固定的成功率。由于目前导航技术的发展,接收机由单频接收机逐渐向多模多频过渡,在有用信息增多的同时搜索的模糊度维数也非常高,因此亟需相关的算法提高其搜索效率,满足实时姿态测量的要求。
致谢: 本文部分实验数据由中国科学院测量与地球物理研究所王海涛副研究员提供,特此感谢!
| [1] |
唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报:信息科学版, 2005, 30(5): 444-446 (Tang Weiming, Sun Hongxing, Liu Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446)
(  0) 0) |
| [2] |
王冰, 隋立芬, 王威, 等. GPS/陀螺组合测姿中整周模糊度的快速解算[J]. 武汉大学学报:信息科学版, 2015, 40(1): 128-133 (Wang Bing, Sui Lifen, Wang Wei, et al. Rapid Resolution of Integer Ambiguity in Integrated GPS/Gyro Attitude Determination[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 128-133)
(  0) 0) |
| [3] |
唐卫明, 李笛, 迟凤明. 北斗卫星导航系统单历元定向算法研究[J]. 武汉大学学报:信息科学版, 2013, 38(9): 1 014-1 017 (Tang Weiming, Li Di, Chi Fengming. Research on Single Epoch Orientation Algorithm of Beidou Navigation Satellite System[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1 014-1 017)
(  0) 0) |
| [4] |
曲建铭, 秦红磊, 金天, 等. 基于基线约束及递推多历元的改进GNSS定姿技术[J]. 解放军理工大学学报:自然科学版, 2014, 15(5): 428-433 (Qu Jianming, Qin Honglei, Jin Tian, et al. Improved Attitude Determination Technique of GNSS Based on Baseline Constraint and Recursive Multiple Epoch[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2014, 15(5): 428-433)
(  0) 0) |
| [5] |
聂志喜, 王振杰, 欧吉坤, 等. 非线性基线长约束条件线性化近似对模糊度解算影响[J]. 测绘学报, 2015, 44(2): 168-173 (Nie Zhixi, Wang Zhenjie, Ou Jikun, et al. On the Effect of Linearization and Approximation of Nonlinear Baseline Length Constraint for Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 168-173)
(  0) 0) |
| [6] |
Teunissen P J G. Integer Least-Squares Theory for the GNSS Compass[J]. Journal of Geodesy, 2010, 84(7): 433-447 DOI:10.1007/s00190-010-0380-8
(  0) 0) |
| [7] |
Giorgi G, Teunissen P J G, Buist P. A Search and Shrink Approach for the Baseline Constrained LAMBDA Method: Experimental Results[C]. International GPS/GNSS Symposium, Tokyo, 2008
(  0) 0) |
| [8] |
Teunissen P J G. Uniqueness and Nonuniqueness of the GNSS Carrier-Phase Compass Readings[M]. Springer Berlin Heidelberg, 2012
(  0) 0) |
| [9] |
Khodabandeh A, Teunissen P J G. Single-Epoch GNSS Array Integrity: An Analytical Study[M]. Springer International Publishing, 2015
(  0) 0) |
| [10] |
Bing W, Lifen S, Guorui X, et al. Comparison of Attitude Determination Approaches Using Multiple Global Positioning System (GPS) Antennas[J]. Geodesy and Geodynamics, 2013, 4(1): 16-22
(  0) 0) |
| [11] |
Park C, Teunissen P J G. Integer Least Squares with Quadratic Equality Constraints and Its Application to GNSS Attitude Determination Systems[J]. International Journal of Control, Automation and Systems, 2009, 7(4): 566-576 DOI:10.1007/s12555-009-0408-0
(  0) 0) |
| [12] |
潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1 210-1 218 (Pan Zongpeng, Chai Hongzhou, Liu Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-Difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1 210-1 218)
(  0) 0) |
| [13] |
Teunissen P J G. The Affine Constrained GNSS Attitude Model and Its Multivariate Integer Least-Squares Solution[J]. Journal of Geodesy, 2012, 86(7): 547-563 DOI:10.1007/s00190-011-0538-z
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China
 2017, Vol. 37
2017, Vol. 37