2. 武汉大学电子信息学院,武汉市珞珈山,430072;
3. 福建工程学院福建省汽车电子与电驱动技术重点实验室,福州市学园路3号,350108
在GNSS定位中,降相关算法可以降低模糊度的方差-协方差矩阵的相关性,减少搜索空间内的候选值个数,从而提高模糊度的搜索效率。有效的评价方法可以更全面地评价降相关算法的降相关性能并提高模糊度解算时的搜索效率,从而选择出综合效率最高的降相关算法。因此,降相关算法的评价方法一直是GNSS降相关领域研究的热点之一[1]。
目前,常用的降相关算法的评价指标主要有条件数[2]、降相关系数[3]和候选值个数[4]等。其中,条件数和降相关系数主要衡量的是降相关算法的降相关性能,只能间接地反映算法的搜索性能。候选值个数虽然可以直接反映降相关算法减少候选值个数的性能以及提高搜索效率,但没有考虑算法本身消耗的时间。因此,3种评价方法都不能从整体上对降相关算法作综合的时间对比分析。而用户最终关心的是整个算法的时间效率,即降相关算法提高的综合时间效率。因此本文采用时间效率(包括降相关时间效率和搜索时间效率)评价方法对算法的整体时间效率进行直接对比分析。基于该方法,通过仿真和实测数据对3种降相关算法作对比分析,得出了一些有价值的结论。
1 3种降相关算法 1.1 整数Gauss降相关整数Gauss降相关算法由Teunissen[5]在LAMBDA算法中首次应用到GNSS模糊度解算领域,具体算法如下。
首先整周模糊度方差-协方差矩阵Qa通过以下过程构造幺模矩阵G。
1) 当qii≤qjj时:
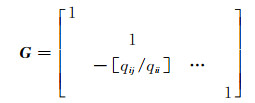
|
(1) |
2) 当qii > qjj时:
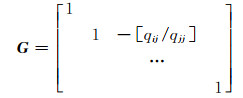
|
(2) |
式中,[·]为取整。
对矩阵G进行求逆,并分别对矩阵Qa进行左乘[G]-1和右乘([G]-1)T,得:
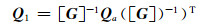
|
(3) |
重复上述过程,直至满足对于所有Qa矩阵中元素都有:
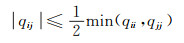
|
(4) |
此时,可得变换矩阵:

|
(5) |
双Chloesky变换降相关算法由Zhou[6]在2011年提出,具体算法如下。
首先对整周模糊度方差-协方差矩阵Qa进行Cholesky LDLT分解, 得:

|
(6) |
对矩阵L进行求逆取整,分别对矩阵Qa进行左乘[L-1]和右乘([L-1])T,得:

|
(7) |
继续对式(7)得到的Q1进行Cholesky UDUT分解,得:
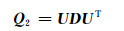
|
(8) |
对矩阵U进行求逆取整,分别对矩阵Q2进行左乘[U-1]和右乘(U-1])T,得:
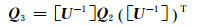
|
(9) |
重复上述过程,直至满足迭代次数或矩阵L或U为单位矩阵。此时,可得变换矩阵:

|
(10) |
LLL规约算法最早由Lenstra、Lenstra和Lovász 3位学者在1982年提出。Hassibi[7]和Grafaren[8]首次将格基规约的思想引入到GNSS模糊度解算中。随后,Xie[9]在论文中对其进行了改进。具体算法如下。
对整周模糊度方差-协方差矩阵Qa进行LLT分解, 并进一步对L进行Gram-Schmidt正交化分解:
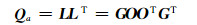
|
(11) |
式中,L为下三角矩阵,G为幺模矩阵,O为近似的正交化矩阵。
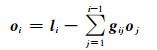
|
(12) |

|
(13) |
式中,l和o分别表示L和O矩阵的行向量,(·)表示内积,[·]表示取整。分别对矩阵Qa进行左乘G-1和右乘(G-1)T,得:
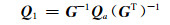
|
(14) |
为了实现LLL规约基的要求,需构造规约变换矩阵,对向量进行逐一处理。
1) 大小规约:利用基向量的正交化系数,构造整数变换矩阵:
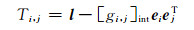
|
(15) |
2) 长度规约:如果
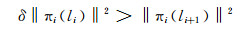
|
(16) |
则对li和li+1的顺序进行调整。其中,πi(li)为li在由前i-1个基向量构成的子格所张成的正交空间上的投影向量。
2 时间效率评价法时间效率评价方法包括两部分的时间效率评价:第一是降相关算法本身的时间效率;第二是降相关之后用搜索方法求最佳解的搜索时间效率。这两部分的时间效率构成了降相关算法总的时间效率。
2.1 降相关时间效率降相关时间效率主要是指降相关算法本身所消耗的时间。即在给定方差-协方差矩阵Qa后,通过降相关算法求出相应的转换矩阵Z的时间消耗。实际应用中,为了更好地减少搜索候选值个数,往往要对方差-协方差矩阵进行排序。因此,为了公平地评价降相关算法本身的时间效率,本文对方差-协方差进行统一的预排序,即3种降相关算法的输入矩阵都是经过预排序的方差-协方差矩阵,其方差-协方差矩阵按对角线降序预排序。
2.2 搜索时间效率搜索时间效率是指通过降相关算法转换方差-协方差矩阵和模糊度浮点解之后,用相应搜索方法确定出最佳解的时间效率。为了公平地评价降相关算法的搜索时间效率,在搜索阶段使用同样的搜索方法,即SE-VB搜索法。
3 实验与分析分别采用仿真和实测数据对3种降相关算法进行时间效率对比分析。为了更明显地呈现出时间效率上的差异,对降相关算法每次循环100次,搜索算法每次循环2 000次。特别指出,示意图以及表格中给出的时间为循环后的总时间。同时,本文所有算法均在Visual Studio2010平台上实现,所用计算机配置为:Intel Core i3处理器、主频3.09 GHz、内存3.42 GB、PC系统为Windows XP。
3.1 仿真数据实验采用随机模拟的方法[10]来构建200个具有对称正定性质的矩阵作为模糊度的方差-协方差矩阵。为更好地模拟实际中卫星的定位情况,本文构建两种维数的方差-协方差矩阵:15维(单系统)和30维(双系统)。
图 1(a)和(b)分别显示了3种算法对15维和30维仿真数据处理的降相关时间效率。可以看出,整数Gauss算法的时间要明显小于双Cholesky和LLL-IGS算法的时间。同时,双Cholesky算法的时间整体也小于LLL-IGS算法的时间。另外,从数值波动范围来看,整数Gauss算法也明显比另外两种算法要稳定,其波动幅度很小,而LLL-IGS算法的波动幅度范围最大。双Cholesky算法的稳定性介于整数Gauss和LLL-IGS两者之间。

|
图 1 仿真数据降相关时间效率 Fig. 1 Decorrelation time efficiency by simulation data |
图 2(a)和(b)分别显示了3种算法对维数15和30的搜索时间效率。从图可见,整数Gauss算法时间最短,双Cholesky算法次之,LLL-IGS算法最长。同时,从时间幅度上可以看出,整数Gauss和双Cholesky算法的时间更稳定,而LLL-IGS的时间幅度波动最大。

|
图 2 仿真数据搜索时间效率 Fig. 2 Search time efficiency by simulation data |
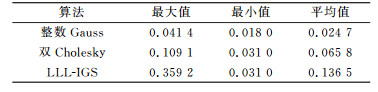
表 1(单位s)和表 2(单位s)分别给出了3种算法对15维和30维的时间效率总和,即降相关时间和搜索时间的总和。由表可见,无论在低维还是高维数据中,整数Gauss算法的时间均最短,算法性能最好;双Cholesky算法次之;LLL-IGS算法效果最差。同时,对比表 1和表 2可见,维数越高,相同降相关算法的降相关时间和搜索时间均越长。
|
|
表 1 算法的总时间对比(15维) Tab. 1 Total time efficiency for simulation(15 D) |
|
|
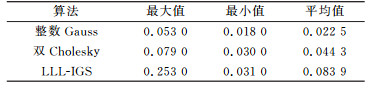
表 2 算法的总时间对比(30维) Tab. 2 Total time efficiency for simulation(30 D) |
实测数据于2015-012-09由Trimble Net R9采集。其基线长度为64 km,采样间隔为15 s,观测时段长度为2 h。
图 3显示了3种算法对实测数据处理的降相关时间效率。可以看出,和仿真数据一样,整数Gauss算法的时间要明显小于双Cholesky算法和LLL-IGS算法的时间。但双Cholesky算法和LLL-IGS算法性能相当。另外,从数值波动范围来看,整数Gauss算法明显比另外两种算法要稳定,其波动幅度很小,而LLL-IGS算法的波动幅度最大。双Cholesky算法的稳定性介于整数Gauss算法和LLL-IGS算法两者之间。

|
图 3 实测数据的降相关时间效率 Fig. 3 The decorrelation time efficiency by real data |
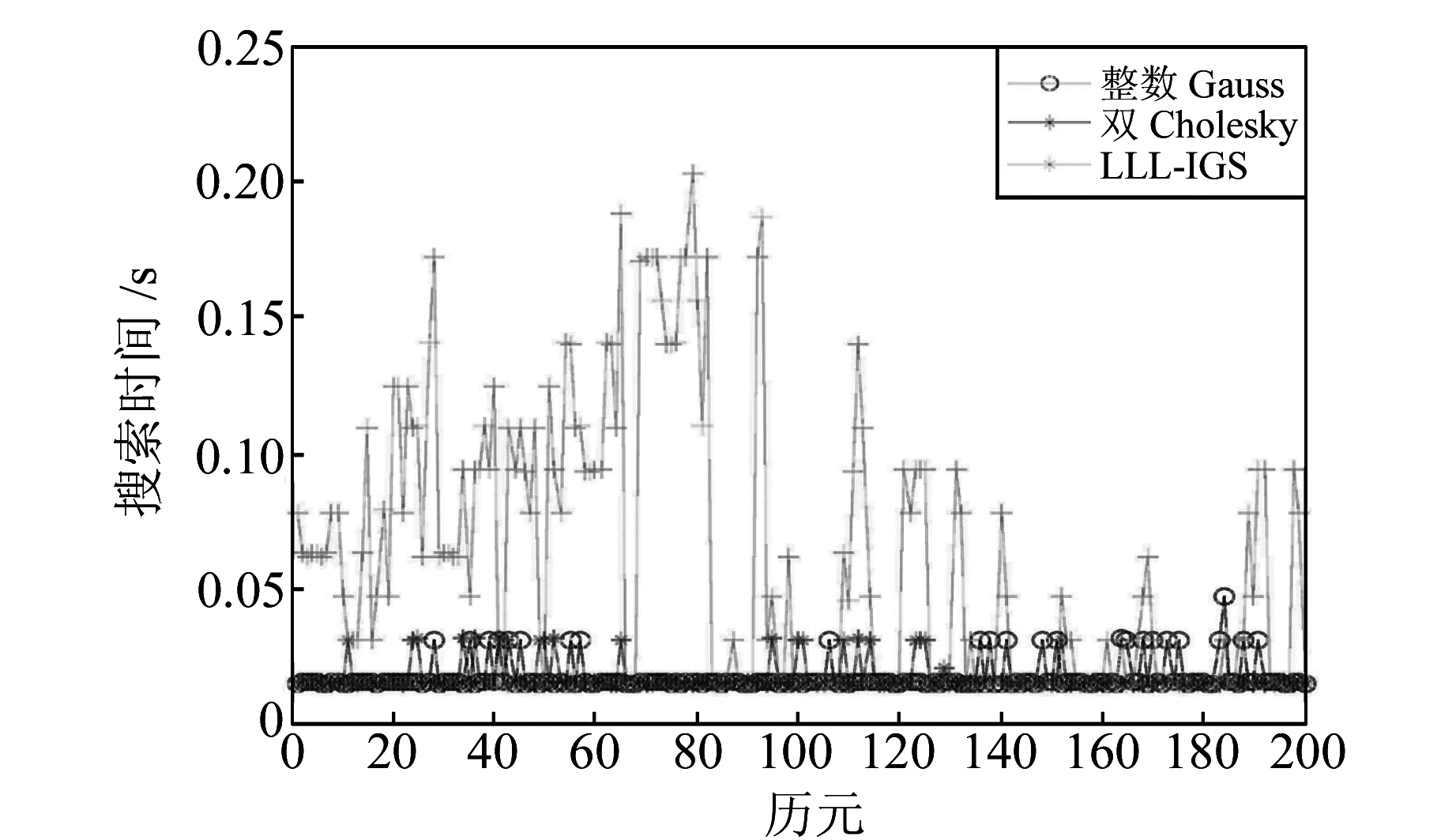
图 4显示了3种算法的搜索时间效率。可以看出,整数Gauss和双Cholesky算法在搜索时间效率上表现几乎一致,而LLL-IGS算法的搜索时间则远远大于前两者。同时,就时间波动幅度来看,整数Gauss和双Cholesky算法表现得也更稳定。
|
图 4 实测数据的搜索时间效率 Fig. 4 The search time efficiency by real data |
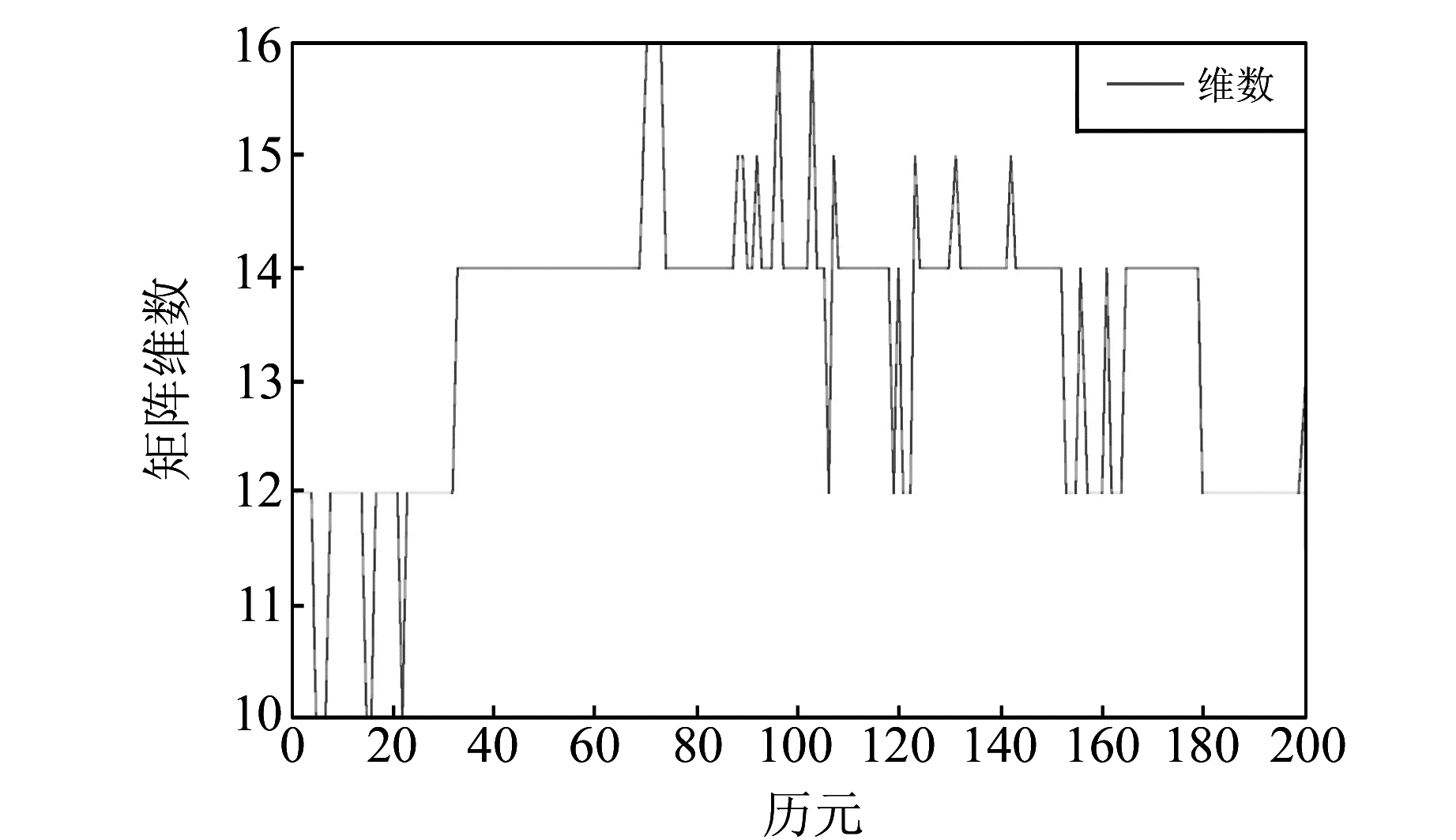
图 5是方差-协方差矩阵维数随历元变化的示意图。可以看出,整体上降相关时间和搜索时间的大小跟矩阵维数大小成正比。但因为整体而言,矩阵维数区别不大,因此,没有仿真数据中15维和30维对比的效果明显。
|
图 5 实测数据中方差-协方差矩阵的维数 Fig. 5 Dimensions of the variance-covariance matrix |
和仿真结果一样,从表 3(单位s)可以看出,整数Gauss算法的时间最短,算法性能最好;双Cholesky算法次之;LLL-IGS算法效果最差。
|
|
表 3 算法的总时间对比(实测数据) Tab. 3 Total time efficiency for real data |
1) 时间效率评价包括降相关时间效率评价和搜索时间效率评价。降相关时间效率主要用于评价算法本身消耗的时间效率,而搜索时间效率主要用来评价降相关算法改善搜索的时间效率。因此,时间效率评价法能从用户最关心的时间因素上对降相关算法作对比分析。
2) 利用仿真和实测数据对3种主流降相关算法进行了时间效率评价分析。实验结果表明,就时间效率而言,整数Gauss算法的效果最好,算法最稳定;双Cholesky算法效果次之;LLL-IGS算法最差。
3) 不同维数情况下,整数Gauss算法性能均表现最好。同时,对同一种降相关算法而言,维数越高,降相关时间和搜索时间消耗平均越多。
| [1] |
卢立果, 刘万科, 李江卫. 降相关对模糊度解算中搜索效率的影响分析[J]. 测绘学报, 2015, 44(5): 481-487 (Lu Liguo, Liu Wanke, Li Jiangwei. Impact of Decorrelation on Search Efficiency of Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 481-487)
(  0) 0) |
| [2] |
Liu L T, Hsu H T, Zhu Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journalof Geodesy, 1999, 73: 478-490
(  0) 0) |
| [3] |
刘志平, 何秀凤, 郭广礼, 等. GNSS模糊度降相关算法及其评价指标研究[J]. 武汉大学学报:信息科学版, 2011, 36(3): 257-261 (Liu Zhiping, He Xiufeng, Guo Guangli, et al. Decorrelation Algorithm and Its Evaluation Indexes for GNSS Ambiguity Solution[J]. Geomatics and Informa-Tion Science of Wuhan University, 2011, 36(3): 257-261)
(  0) 0) |
| [4] |
Shahram Jazaeri S, Amiri-Simkooei A, Sharifi M A. On Lattice Reduction Algorithms for Solving Weighted Integer Least Squares Problems:Comparative Study[J]. GPS Solutions, 2014, 18(1): 105-114 DOI:10.1007/s10291-013-0314-z
(  0) 0) |
| [5] |
Teunissen P J G. A New Method for Fast Carrier Phase Ambiguity Estimation[C]. IEEE PLANS'94, Las Vegas, 1994 http://www.researchgate.net/publication/3571567_A_new_method_for_fast_carrier_phase_ambiguity_estimation
(  0) 0) |
| [6] |
Zhou Y. A New Practical Approach to GNSS High-Dimensional Ambiguity Decorrelation[J]. GPS Solutions, 2011, 15(4): 325-331 DOI:10.1007/s10291-010-0192-6
(  0) 0) |
| [7] |
Hassibi A, Boyd S. Integer Parameter Estimation in Linear Models with Applications to GPS[J]. IEEE Trans Signal Process, 1998, 46(11): 2 938-2 952 DOI:10.1109/78.726808
(  0) 0) |
| [8] |
Grafarend E W. Mixed Integer-Realvalued Adjustment(IRA) Problems: GPS Initial Cycle Ambiguity Resolution by means of the LLL Alogrrithm[J]. GPS Solutions, 2000, 4(2): 31-44 DOI:10.1007/PL00012840
(  0) 0) |
| [9] |
谢恺, 柴洪洲, 范龙, 等. 一种改进的LLL模糊度降相关算[J]. 武汉大学学报:信息科学版, 2014, 39(11): 1 363-1 368 (Xie Kai, Chai Hongzhou, Fan Long, et al. An Improved LLL Ambiguity Decorrelation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1 363-1 368)
(  0) 0) |
| [10] |
Chang X, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Algorithm for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
2. School of Electronic Information, Wuhan University, Luojia Hill, Wuhan 430072, China;
3. Fujian Key Laboratory of AED, Fujian University of Technology, 3 Xueyuan Road, Fuzhou 350108, China
 2017, Vol. 37
2017, Vol. 37