2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
载波相位数据的预处理是获取高精度定位结果的前提,其主要工作是进行周跳的探测与修复。目前,利用非差的双频观测数据进行周跳探测的方法主要有多项式拟合法、电离层残差法、TurboEdit算法等[1-5]。多项式拟合算法对于1周的小周跳不敏感。电离层残差法可以顺利地探测出小周跳的存在,但无法确定周跳发生的频率、大小、历元,同时存在对一些周跳组合不敏感的情况。MW组合法也存在对于某些周跳无效的情况。当卫星高度角较低时,多路径效应影响明显,观测数据质量差,使用固定而经验化的判定阈值进行周跳检测,容易出现误判或漏判的情况。
因此,本文在TurboEdit方法的基础上,顾及高度角对观测数据质量的影响,重新设定周跳检测量的判定阈值进行周跳判断。针对MW组合,使用高度角定权,并结合移动窗口,计算宽巷模糊度的平滑值和中误差。对于电离层残差法,使用电离层残差组合在历元间求二次差构造周跳检测量,进行周跳的判断[6]。当检测出周跳存在时,利用搜索法确定周跳的大小,保证周跳修复的可靠性。选用实测的GPS数据进行算法测试的结果表明,本文方法可实现周跳的实时探测与修复。
1 顾及高度角的移动窗口MW组合探测法MW组合是伪距和相位进行组合以消除电离层、对流层误差,是周跳探测中常用的组合方式。其公式为[7]:
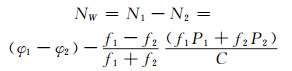
|
(1) |
式中,NW为宽巷模糊度,N1、N2分别为两个频点的整周模糊度,φ1、φ2为载波相位观测值,f1、f2为载波信号的频率,P1、P2为对应的伪距观测值。宽巷模糊度的平均值和中误差的计算公式为[2]:
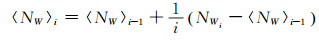
|
(2) |
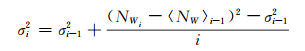
|
(3) |
式中,〈NW〉i和σi2分别为经过等权递推计算得到的各历元的宽巷模糊度递推均值和中误差。若宽巷模糊度值NW与宽巷模糊度递推值〈NW〉i-1满足式(4),表示该历元处的观测数据包含周跳。
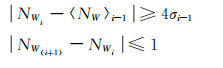
|
(4) |
GNSS测量时卫星高度角不断发生变化,当卫星高度角较低时,数据质量较差。MW组合法使用之前历元的所有数据,通过式(2)进行宽巷模糊度的递推计算,未考虑卫星高度角对数据质量的影响。若使用之前的全部数据将会使数据质量较好的历元受到影响,可能增加周跳漏判或错判的概率。因此,引入时间窗口并且顾及高度角进行定权,对MW组合进行改进,即计算〈NW〉i时不再使用之前的全部观测数据进行等权平均,改为使用之前的部分数据加权滑动平均。具体步骤如下:确定合适的移动窗口大小n,利用当前历元i之前的n个历元观测数据通过式(5)计算宽巷模糊度的平滑值,宽巷模糊度的中误差可通过式(6)计算得到,利用式(4)判断周跳是否存在。当i=1时,σ取0.5。假设探测到该历元存在周跳即进行周跳的修复,待该历元周跳修复结束后,移动到之后一历元继续计算,直至最后一个历元。本文中采用固定窗口长度的加权滑动平均,每次仅向后滑动一个历元,以保证在所选择的窗口长度内至多有一个历元存在周跳,方便实现周跳的修复,同时可以提高周跳探测修复的可靠性。
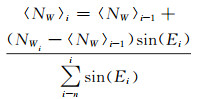
|
(5) |
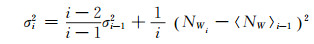
|
(6) |
对于时间窗口长度的选取,时间窗口的长度过短,未平滑的测量噪声将会影响到周跳判定阈值(σ2),导致频繁出现不规则的波动;时间窗口的长度过长,在计算周跳判定阈值的时候可能选择与当前历元数据质量相差较大的数据,造成阈值计算不合理的情况,从而导致周跳检测不准确。对于不同质量、不同采样率的数据,都可以通过实验对时间窗口的长度进行调整。
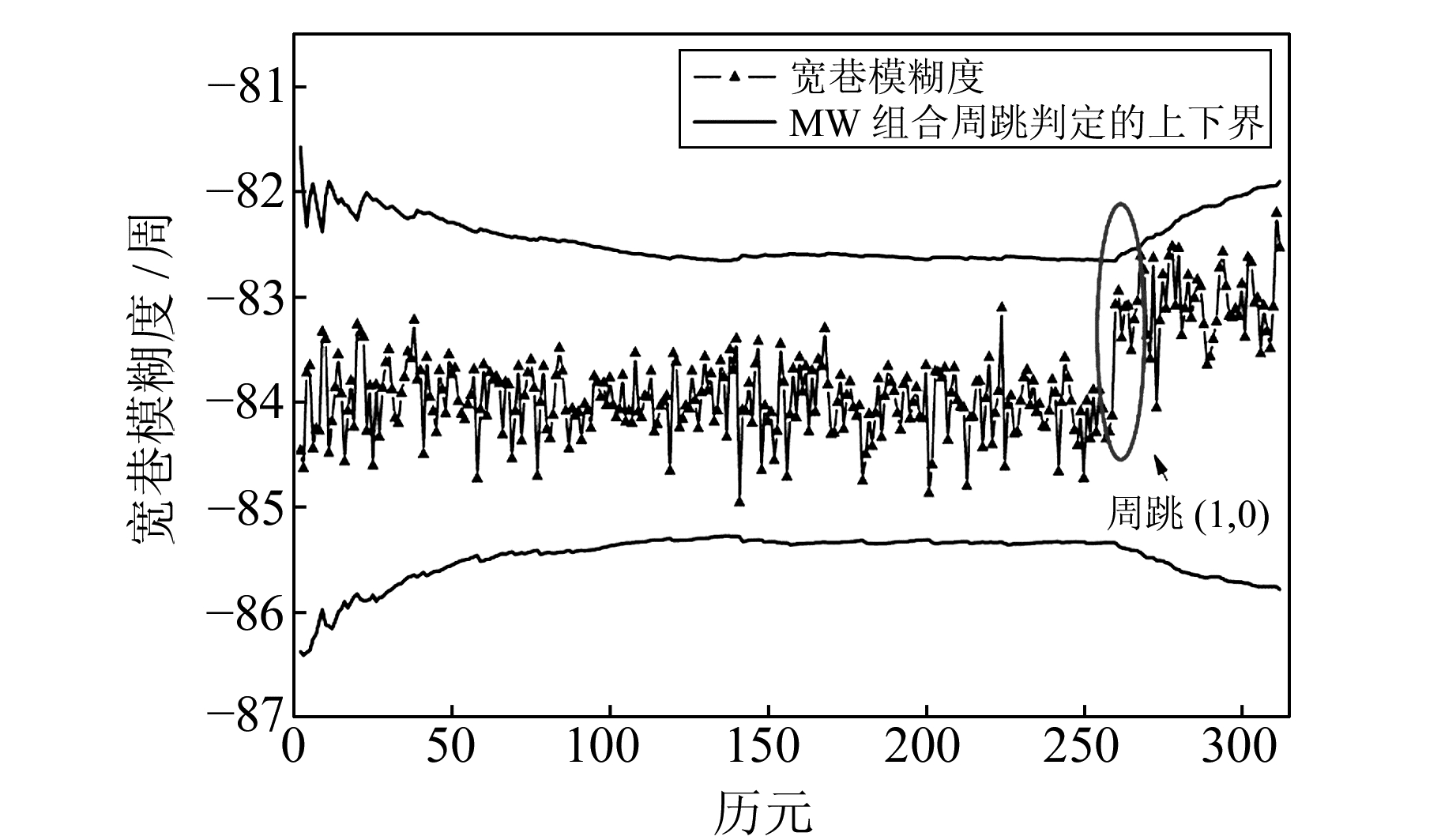
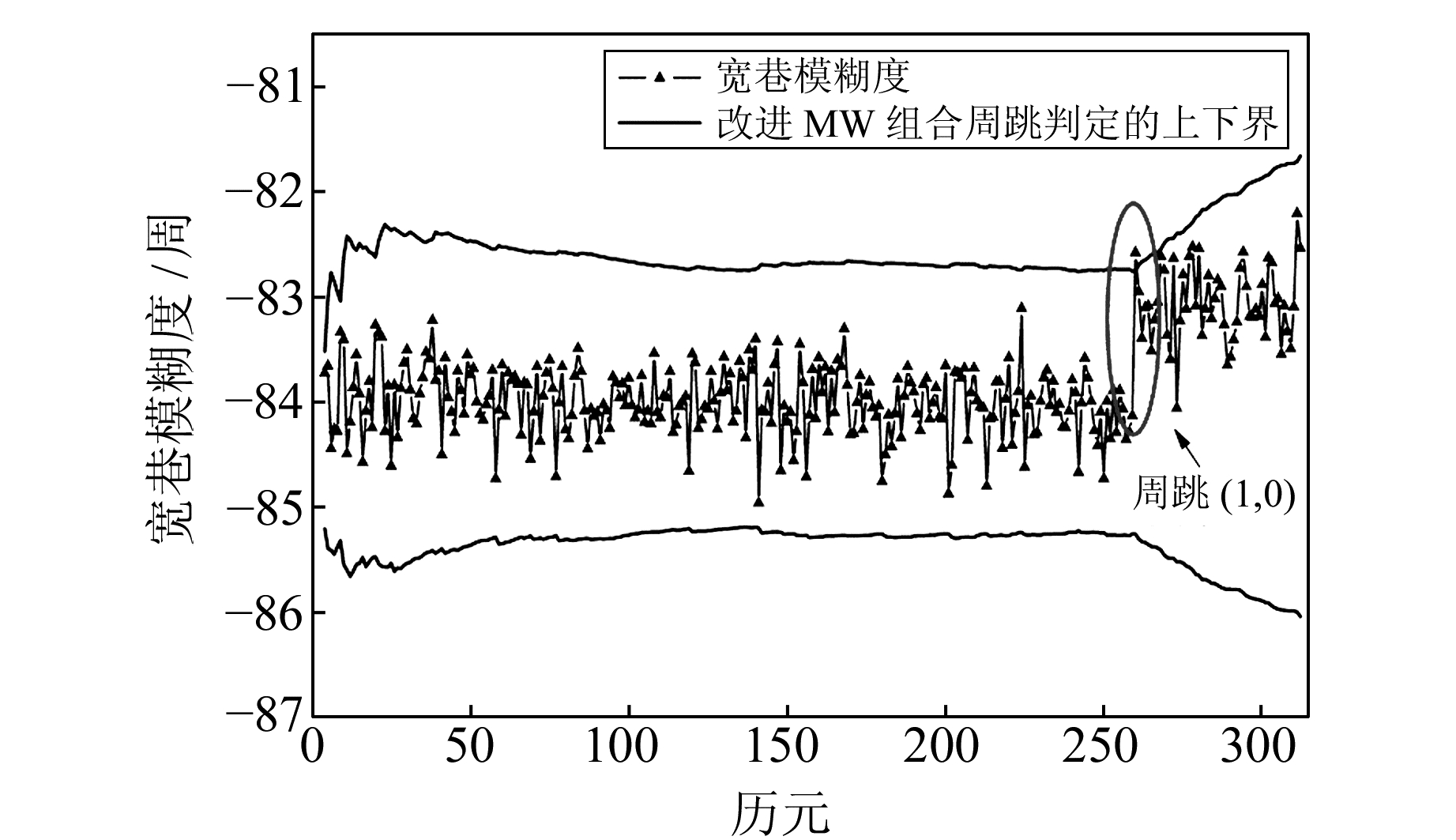
选用2014-01-01 BJFS站PRN08号卫星04:01:00~06:37:00的实测数据进行实验。在第260历元(06:10:30)处给L1频率上人为加入1周的周跳。分别采用TurboEdit方法中的MW组合法及本文改进的MW组合探测法进行周跳探测,两种方法的探测结果分别如图 1、图 2所示。从图 1可以看出,使用传统的MW方法无法探测(1, 0)周跳的存在,当使用改进的MW组合方法时,图 2中周跳检验量在第260历元处超出阈值,(1,0)周跳被准确探测。导致这种情况的原因是,改进的方法考虑了高度角对观测质量的影响,并结合移动窗口进行计算,更为合理地计算周跳检测量,提高了周跳探测的成功率。
|
图 1 传统的TurboEdit方法探测(1, 0)周跳 Fig. 1 Cycle slip detection results for GNSS PRN08 using the traditional MW method at BJFS on Jan.1, 2014 |
|
图 2 改进的MW方法探测(1, 0)周跳 Fig. 2 Cycle slip detection results for GNSS PRN08 using the improved MW method at BJFS on Jan.1, 2014 |
GF组合的计算公式如下[8]:
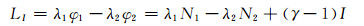
|
(7) |
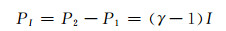
|
(8) |
再利用多项式Q对PI进行拟合。通过式(9)判断载波观测值中是否包含周跳:
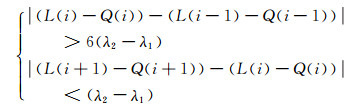
|
(9) |
上述周跳检测方法中,利用多项式拟合取代伪距电离层残差组合。而多项式拟合与拟合阶数及选取的多项式类型有关,从而降低数据处理的客观性[9],可能影响周跳的探测结果。本文采取相邻历元之间载波相位电离层残差组合求二次差的方式进行计算:
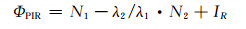
|
(10) |
式(10)称为电离层残差组合。式中,γ=f12/f22,IR=(γ-1)I, I为发生在L1频率上的电离层延迟,其他符号意义同上。
对于所采集的观测数据,相邻历元之间观测条件基本相同或相似,观测数据中包含的误差基本相同,通过历元之间作差,可以削弱电离层误差的影响,利于周跳探测。
一阶电离层残差组合为:
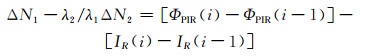
|
(11) |
为了尽可能地削弱电离层误差的影响,在一阶电离层残差组合的基础上进行求差,得到二阶电离层残差组合:
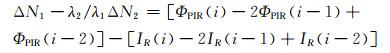
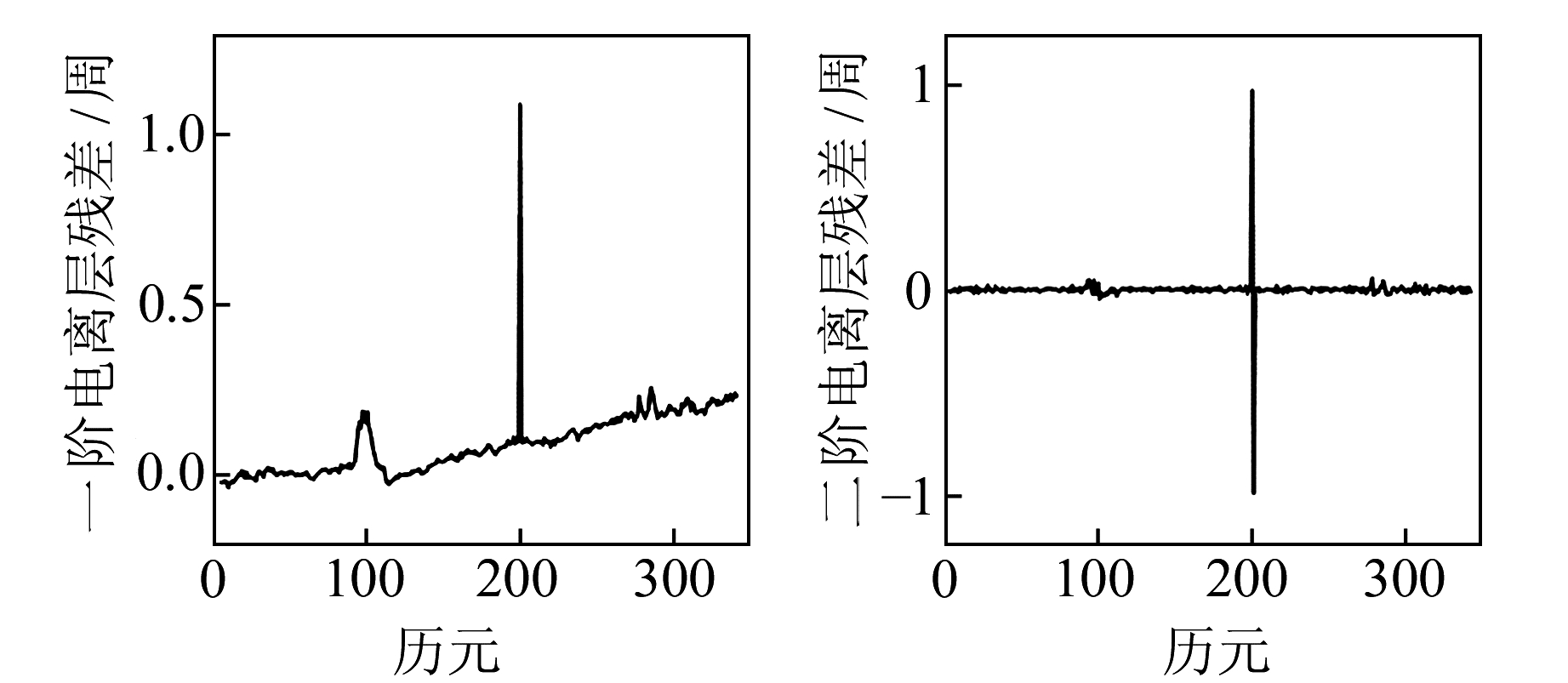
|
(12) |
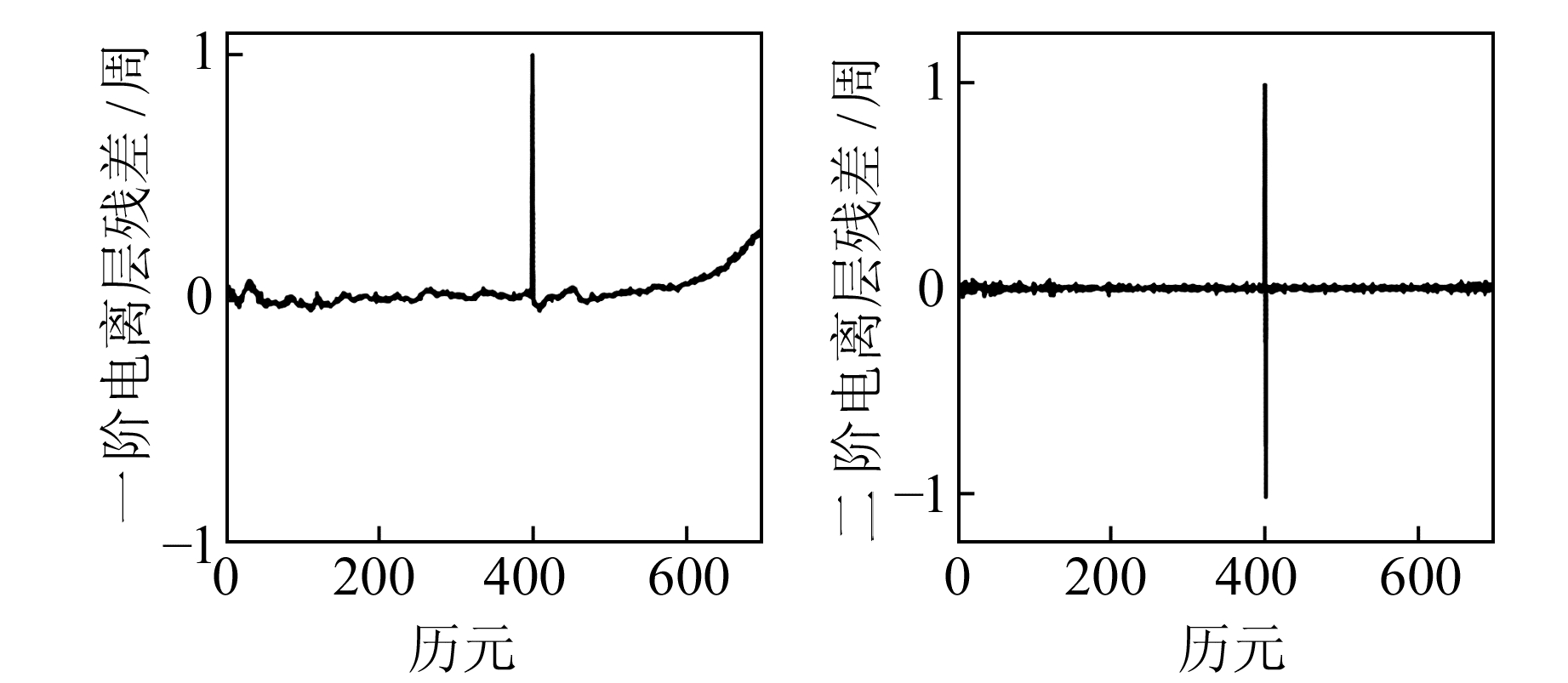
本文选取BJFS站2014-01-01 PRN2卫星观测数据,在400历元处加入(1, 0)小周跳进行测试,绘制一阶电离层残差和二阶电离层残差对比图(图 3)。可以发现,二阶电离层残差值的波动相较于一阶电离层残差更加平稳,只在周跳发生时发生突变,这样可以很容易发现周跳的发生。通过文献[6]可以得知,2001-04-15电离层比较活跃,其中15:00左右较为显著。因此,选择AMC2站PRN26卫星13:00:00~16:00:00的观测数据进行实验,在200历元处加入(1, 0)周跳得到图 4。可以看出,在电离层活跃期间,二阶电离层残差比一阶电离层残差效果好,与图 3的结论一致。
|
图 3 BJFS站2014-01-01 PRN2卫星一阶电离层残差和二阶电离层残差对比 Fig. 3 Cycle slip detection results for GNSS PRN2 using PIR method at BJFS on Jan 1, 2014 |
|
图 4 AMC2站2001-04-15 PRN26卫星一阶电离层残差与二阶电离层残差对比 Fig. 4 Cycle slip detection results for GNSS PRN26 using PIR method in high ionospheric activity at AMC2 on April 15, 2001 |
改进MW组合法和二阶电离层残差组合法都可以实现周跳探测的目的,但也存在一些不足。当发生大小相同的周跳时,MW组合无法判断出周跳的存在。当两个频率的周跳与波长成比例时,二阶电离层残差法失效,本文称这样的组合为不敏感组合。单独使用这两种方法,可以探测出周跳存在的历元,但不知道周跳的大小,以及所在的频率。因此,将两种方法相结合,可以弥补各自的不足,并通过式(13)确定周跳的大小和频率:
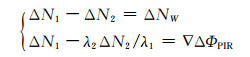
|
(13) |
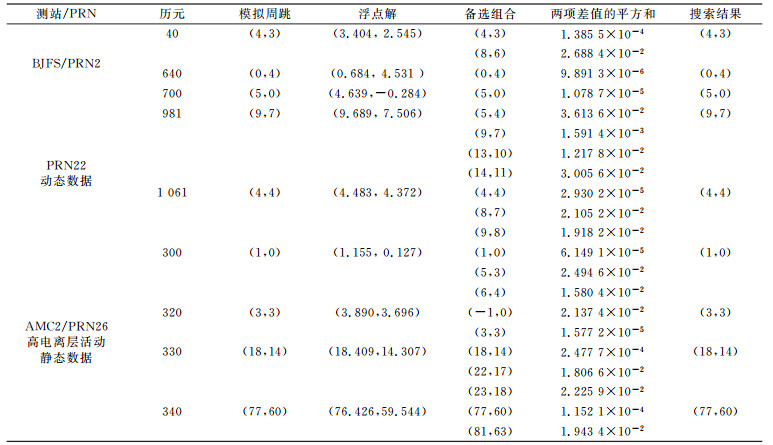
为了更加准确地确定周跳的固定解,避免因四舍五入等原因造成所确定的周跳不正确,采用搜索算法[10]确定周跳。具体步骤如下:
1) 将式(13)求得的浮点解四舍五入,作为周跳的初始值;
2) 在周跳初始值上以[-5, 5]为区间,以1周为步长循环计算,组成新的周跳组合;
3) 利用新周跳组合对载波观测值进行修复,并通过两种方法进行周跳探测,记录同时满足两种周跳检测条件的周跳组合;
4) 将符合条件的周跳组合的宽巷模糊度递推值与上一历元的宽巷模糊度的递推值作差,同时重新计算该历元的二阶电离层残差值,两项差值的平方和值最小((〈NW〉i-〈NW〉i-1)2+(ΔN1-λ2ΔN2/λ1)2=min)的周跳组合即为周跳固定解。
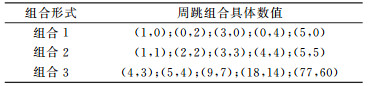
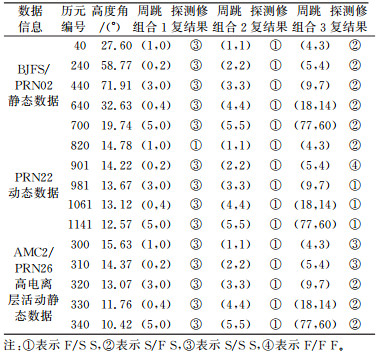
4 实验与分析为验证本文中所提出方法的实际效果,采用在“干净”的观测数据中加入模拟周跳的方式进行实验。选择静态、动态观测数据以及高电离层活动时静态观测数据分别进行实验。其中静态观测数据选择BJFS站2014-01-01 00:01:00~06:26:00 PRN2卫星的观测数据,采样率为30 s。动态观测数据选用2011-07-15 02:33:38~02:52:55 PRN22卫星的观测数据,采样率为1 s。电离层活跃期间,选择AMC2测站PRN26号卫星13:00:00~16:00:00数据进行测试,其采样率为30 s。经测试,选用的实验数据均不存在周跳。采用表 1所示的周跳组合人为模拟周跳进行测试。
|
|
表 1 拟加入的周跳组合 Tab. 1 Simulative cycle slip combination |
采用上述方案使用改进方法进行周跳探测,实验结果汇总见表 2,使用文中所述的搜索方法进行周跳修复的部分统计结果见表 3。表 2中3个字母依次表示改进MW组合法、二阶电离层残差法的周跳探测情况及周跳搜索成功与否。如S/S S表示改进MW组合法和二阶电离层残差法均成功探测出周跳,周跳搜索正确。
|
|
表 2 周跳探测结果 Tab. 2 The results of cycle slip detection |
|
|
表 3 周跳搜索结果 Tab. 3 The results of cycle slip searching |
从表 2可以看出,本文提出的改进方法可以成功探测出组合1中的所有周跳,对于改进的MW组合法,在低高度角情况下,仍具有良好的探测效果。组合2中的周跳组合是MW组合法的探测盲区,但二阶电离层残差法成功探测出等周周跳的存在。同时在电离层活跃期间,二阶电离层残差法的探测结果证明该方法对电离层影响不敏感,依旧可以正确探测周跳。组合3是电离层残差法不敏感的周跳组合,改进的MW组合成功探测出其中多数周跳组合,并实现了正确修复,弥补了二阶电离层残差法的不足,但在动态数据第901历元时,改进的MW组合未能成功探测出(5, 4)组合,可能与观测时刻的数据质量存在一定的关系。从表 3可以看出,通过文中所述的周跳搜索方法确定的周跳值与添加的模拟周跳相同,证明该搜索方法可以正确确定周跳的大小,具有一定的可靠性。
5 结语本文根据高度角对于数据质量的影响,对MW组合法进行了改进。将高度角定权和移动窗口相结合,使MW组合中周跳判定阈值计算更为合理。同时,通过历元间二阶电离层差分,进一步削弱电离层误差的影响,有利于周跳检测。最后提出一种周跳搜索方法确定周跳大小。结合改进的两种方法和周跳搜索法,使得周跳探测与修复的成功率得以提高。分别采用静态数据和动态数据进行算法正确性的测试,结果表明,该算法可实现小周跳、大周跳的探测与实时修复,且模型简单、便于实现,为GNSS数据后续处理奠定了基础。
| [1] |
Liu Z Z. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3): 171-183 DOI:10.1007/s00190-010-0426-y
(  0) 0) |
| [2] |
Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [3] |
Xu G C. GPS: Theory, Algorithms and Applications[M]. Berlin: Springer, 2007
(  0) 0) |
| [4] |
周海涛, 吕志平, 许国昌, 等. 一种基于数据质量分析的改进TurboaEdit方法[J]. 海洋测绘, 2016, 36(1): 25-30 (Zhou Haitao, Lü Zhiping, Xu Guochang, et al. An Improved TurboEdit Method Based on Data Quality Analysis[J]. Hydrographic Surveying and Charting, 2016, 36(1): 25-30 DOI:10.3969/j.issn.1671-3044.2016.01.006)
(  0) 0) |
| [5] |
范士杰, 陈冠旭, 刘焱雄, 等. 低高度角双频非差数据的周跳探测方法研究[J]. 武汉大学学报:信息科学版, 2016, 42(3): 310-315 (Fan Shijie, Chen Guanxu, Liu Yanxiong, et al. Cycle-Slip Detection Methods for Dual-Frequency Undifference Data at Low Elevation Angle[J]. Geomatics and Information Science of Wuhan University, 2016, 42(3): 310-315)
(  0) 0) |
| [6] |
Cai C S, Liu Z Z, Xia P F, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observation under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247-260 DOI:10.1007/s10291-012-0275-7
(  0) 0) |
| [7] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [8] |
李林阳, 吕志平, 周海涛, 等. 对TurboEdit周跳探测及修复算法的改进[J]. 测绘科学与技术学报, 2015, 32(2): 140-145 (Li Linyang, Lü Zhiping, Zhou Haitao, et al. Improvement of the TurboEdit Cycle Slip Detection and Repair Algotithm[J]. Journal of Geomatics Science and Technology, 2015, 32(2): 140-145)
(  0) 0) |
| [9] |
李慧茹, 黄观文, 赵敏宁, 等. TurboEdit方法中周跳检测算法的改进[J]. 时间频率学报, 2012, 35(1): 43-49 (Li Huiru, Huang Guanwen, Zhao Minning, et al. Improvement of Cycle Slip Detecion in TurboEdit Algorithm[J]. Journal of Time and Frequency, 2012, 35(1): 43-49 DOI:10.3969/j.issn.1674-0637.2012.01.008)
(  0) 0) |
| [10] |
郑作亚, 程宗颐, 黄珹, 等. 对Blewitt周跳探测与修复方法的改进[J]. 天文学报, 2005, 46(2): 216-224 (Zheng Zuoya, Cheng Zongyi, Huang Cheng, et al. Improving of Cycle Slip Detection and Correction of Blewitt Method[J]. Acta Astronomica Sinica, 2005, 46(2): 216-224 DOI:10.3321/j.issn:0001-5245.2005.02.013)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37