周跳处理是GNSS数据预处理的重要环节,常规双频周跳探测算法有TurboEdit算法、高次差法、贝叶斯估计的非差法等[1]。随着GNSS技术的发展,多频数据为周跳处理提供了更多长波长、弱电离层延迟、低噪声的三频组合方式[2-3]。常规三频周跳探测方法有三频伪距/载波组合、三频相位无几何组合法等[4-7]。双频与三频周跳探测方法均考虑电离层平稳变化,可忽略历元间电离层延迟变化的影响,但当电离层变化剧烈或发生磁暴时,历元间电离层延迟变化较大[8-9],常规方法已不再适用,需要考虑电离层变化活跃时的周跳探测算法。文献[10]利用电离层残差历元间两次差分与MW结合,文献[11]利用TECR算法扣除掉电离层速率项探测周跳,并使用高采样率数据进行验证,但算法主要针对高电离层活动下的双频数据,不能满足多频周跳探测需要。关于多频部分,文献[12]基于假设检验同时分析了周跳、粗差、电离层异常;文献[13]提出三频TurboEdit算法,利用两次差分的无几何相位组合与三频无几何无电离层码相组合进行周跳探测,但算法阈值设置单一,不能反映实时数据变化。基于此,本文考虑高电离层变化,提出一种更有效的三频周跳处理方法,以体现三频技术的优势。
1 削弱电离层延迟的三频TECR算法 1.1 三频TECR算法双频TECR算法拟合电离层速率后能有效消除电离层延迟影响,将双频TECR算法推广到三频,忽略多径变化影响,构造无几何相位组合为[2-3]:
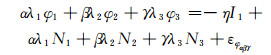
|
(1) |
式中,α、β、γ为载波观测值系数,λk、φk、Nk(k=1, 2, 3)分别表示3个频点的波长、载波观测值、整数模糊度,I1为第一频点的电离层延迟,εφαβγ为组合噪声。
为消除站星几何影响,令站星距离系数α+β+γ=0,电离层组合系数η为:
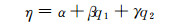
|
(2) |
式中,q1=f12/f22,q2=f12/f32。
对式(1)进行历元间求差,得组合周跳:
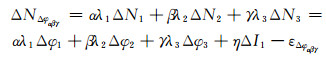
|
(3) |
设原始载波观测噪声为σφ(单位:rad),且观测值间相互独立,则历元间组合周跳的标准差为:
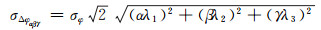
|
(4) |
由式(1)得三频电离层总电子含量(total electron contents, TEC)为:

|
(5) |
对式(5)历元间作差,得电离层速率(total electron contents rate,TECR)为:
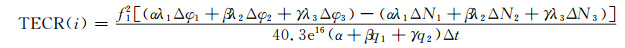
|
(6) |
式中,i表示历元序号,Δt表示采样间隔。
为削弱电离层延迟影响,可减少三频无几何组合系数η,对电离层速率进行拟合作差。令载波噪声为0.01 rad[5],优化三频无几何相位组合,结果见表 1。
|
|
表 1 三频无几何相位组合 Tab. 1 Three-frequency geometry-free phase combination |
文献[11]采用固定30历元对电离层速率进行拟合,由于不同观测段内数据质量不同,采用固定历元数进行拟合并不合理,需确定最优拟合历元数。因载波观测精度较高,可分析其拟合残差,确定当前历元前数据波动最平稳的数据段,然后利用最小二乘拟合电离层速率,得到拟合值TECR(i)Q。将拟合值与电离层速率作差得拟合残差Tcci:
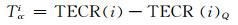
|
(7) |
确定最优拟合历元数的方法为:选取前n个历元的电离层拟合残差值Tcci进行质量分析,并依次减少最前面一个Tcci,得到不同的质量结果,在这些结果中找到最优数据质量的那一组历元数作为最优拟合历元数window。选取前window个TECR(i)拟合得到TECR(i)Q,一般取拟合阶数为3即可满足精度要求。观测数据质量情况利用标准差进行判断:
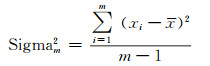
|
(8) |
式中,m=n, n-1, …, 6;xi为电离层拟合残差;x为残差平均值。为保证拟合有效性,n的下限设为6。利用文献[11]所设置的30个历元作为n的上限,通过搜索发现,在选取标准差最小的最优拟合历元数中,平均历元数为12。加大n的上限分析最小标准差发现,并不是拟合历元数越多拟合效果越好,这是因为不同时间段数据质量不同,当前面观测数据质量较差时会影响标准差。为提高计算效率及得到合理的拟合历元数,n的上限设为15,在电离层极端变化时,可适当增大。
表 1中num表示在设置4σΔφαβγ为探测阈值(99.88%的置信水平)时,在1~100 rad内搜索的对应组合的不敏感周跳个数;加粗部分4σΔφαβγ较小,有利于小周跳探测;下划线部分电离层延迟系数较小,但4倍中误差较大,不利于小周跳探测。电离层延迟误差经TECR算法削弱后,影响探测精度的主要是载波观测噪声,需要选取噪声最小的无几何相位组合作为周跳探测量,而GPS和BDS噪声4σΔφαβγ最小均为[1, -1, 0]和[1, 0, -1]组合,故选取这两组无几何相位组合求解TECR。三频观测值可得到η和σΔφαβγ更小的组合,更有利于周跳探测,但由于无几何组合只有两个组合线性无关,每个组合均存在较多不敏感周跳。若任意两个无几何组合相结合可有效减少不敏感周跳个数,但仍存在两个无几何组合均不敏感的周跳组合,即GPS(59, 46, 44)、(91, 71, 68)和BDS(75, 58, 61),此时该不敏感周跳组合可通过三频码相无几何无电离层组合进行补充探测。
1.2 三频码相无几何无电离层组合三频码相无几何无电离层组合为:
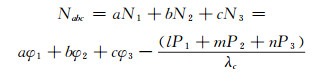
|
(9) |
式中,Nabc为三频码相组合模糊度,λc为组合波长,Pk(k=1, 2, 3)为伪距观测值,a、b、c为载波组合系数,l、m、n为伪距组合系数。
由于伪距噪声远大于载波噪声,为保证组合噪声影响尽可能小,应使组合波长λc尽可能大,伪距系数组合尽可能小,故在给定载波系数的前提下,伪距观测系数应满足:
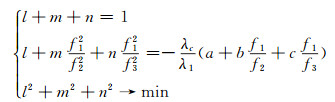
|
(10) |
当发生周跳时,对式(9)历元间作差得周跳检验量:

|
(11) |
顾及原始载波、伪距观测值间相互独立,得组合模糊度的标准差:
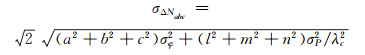
|
(12) |
令GPS和BDS伪距噪声为0.3 m、载波噪声为0.01 rad,优化三频组合见表 2。
|
|
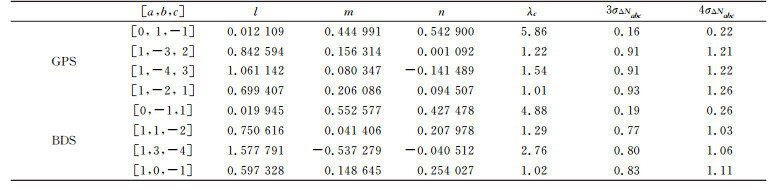
表 2 三频码相无几何无电离层组合 Tab. 2 Triple-frequency code-phase geometry-free and ionospheric-free combination |
考虑三频码相无几何无电离层组合对小周跳探测的灵敏性,需要组合中误差4σΔNabc较小。文献[14]指出,组合中误差4σΔNabc越小,周跳取整的成功率越高,对周跳修复越有利。而GPS组合[0, 1, -1]和BDS组合[0, -1, 1]的4σΔNabc仅占对应波长的4%和6%,满足需要;其余组合虽波长较长,但组合中误差均达到1 rad,不利于小周跳的探测。故本文选取GPS组合[0, 1, -1]和BDS组合[0, -1, 1]作为三频码相无几何无电离层组合系数进行周跳探测。三频码相组合载波系数和为0,不能探测到ΔN1=ΔN2=ΔN3类型的周跳,但可通过三频TECR算法进行补充探测。
1.3 周跳探测与修复由§1.1可知,不同观测时段的观测数据质量不同,当阈值与真实数据的动态变化一致时,可避免周跳的误探与漏探。利用最优拟合历元数window,借鉴MW方法中阈值计算过程[15],得到三频TECR方法中两种组合的阈值递推公式:
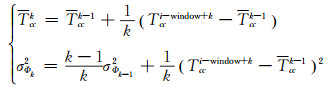
|
(13) |
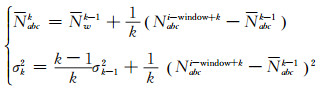
|
(14) |
式中,Tcck-1为TECR拟合残差递推值,σΦk为TECR拟合残差中误差,k表示window内的第k个数据,Nabck、σk表示三频码相无几何无电离层组合组合模糊度递推值和中误差。
当满足式(15)时即可认为当前历元发生周跳,如果当前历元i发生周跳,则阈值会发生较大突变,可能发生漏探。为保证探测准确性,均采用前一历元的中误差作为当前历元的检核中误差,采用4倍阈值可保证99.99%的置信水平。
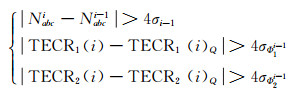
|
(15) |
当发生周跳时,修复探测到的周跳:
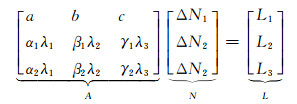
|
(16) |
式中,α1、β1、γ1和α2、β2、γ2分别为两个三频TECR组合的系数,Lk(k=1, 2, 3)分别为对应的周跳探测检测量。由于三频码相无几何无电离层组合系数为整数,可对周跳检测量L1直接取整固定。
受观测噪声影响,有时会存在周跳修复失败的情况,需经过简单搜索确定正确周跳值:对解算的周跳值N在前后5 rad内进行小范围搜索,若满足式(16)则作为备选周跳组合,然后对备选周跳组合进行1范数求解,得到最小1范数对应的周跳即为当前历元的正确周跳。最小1范数表达式为:
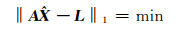
|
(17) |
式中,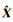
2013-03-17发生大磁暴[15],选取TEC变化显著的GMSD站点(30.55°N, 131.01°E)观测到的G24和C06号卫星数据进行分析,接收机为Trimble NETR9,采样间隔为30 s,卫星高度角大于10°。利用GPS三频码相无几何无电离层组合[0, 1, -1]与三频TECR组合[1, -1, 0]和[1, 0, -1]、BDS三频码相无几何无电离层组合[0, -1, 1]与三频TECR组合[1, -1, 0]和[1, 0, -1]进行电离层活跃期下三频周跳的探测与修复实验。
图 1给出了未削弱电离层延迟的TECR算法及其阈值结果。可以看出,未削弱电离层延迟的GPS与BDS三频TECR组合分别在0~100历元与900~1 200历元超出阈值,导致无法进行周跳探测;GPS码相无几何无电离层组合在300~400历元超出阈值,导致周跳误探。这表明常规算法已不能满足电离层活跃期的周跳探测,且阈值也无法实时反映数据动态变化。
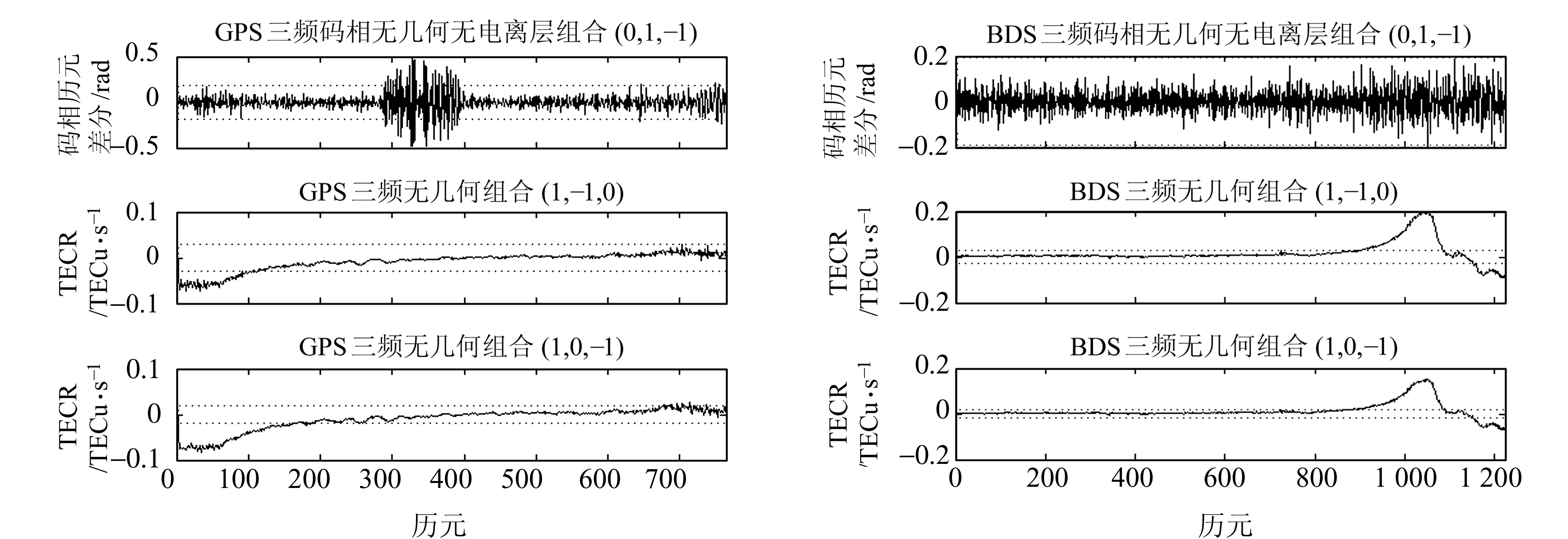
|
图 1 未削弱电离层延迟的三频TECR算法及其阈值 Fig. 1 Three-frequency TECR algorithm with ionospheric delay and the threshold |
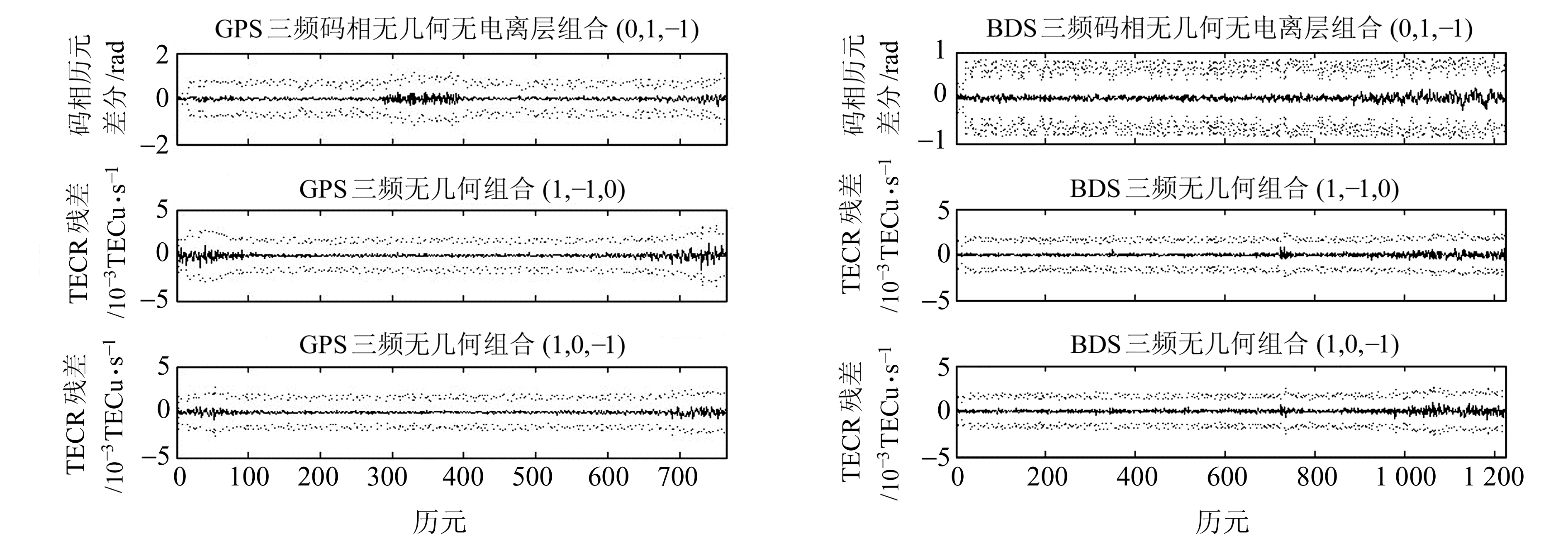
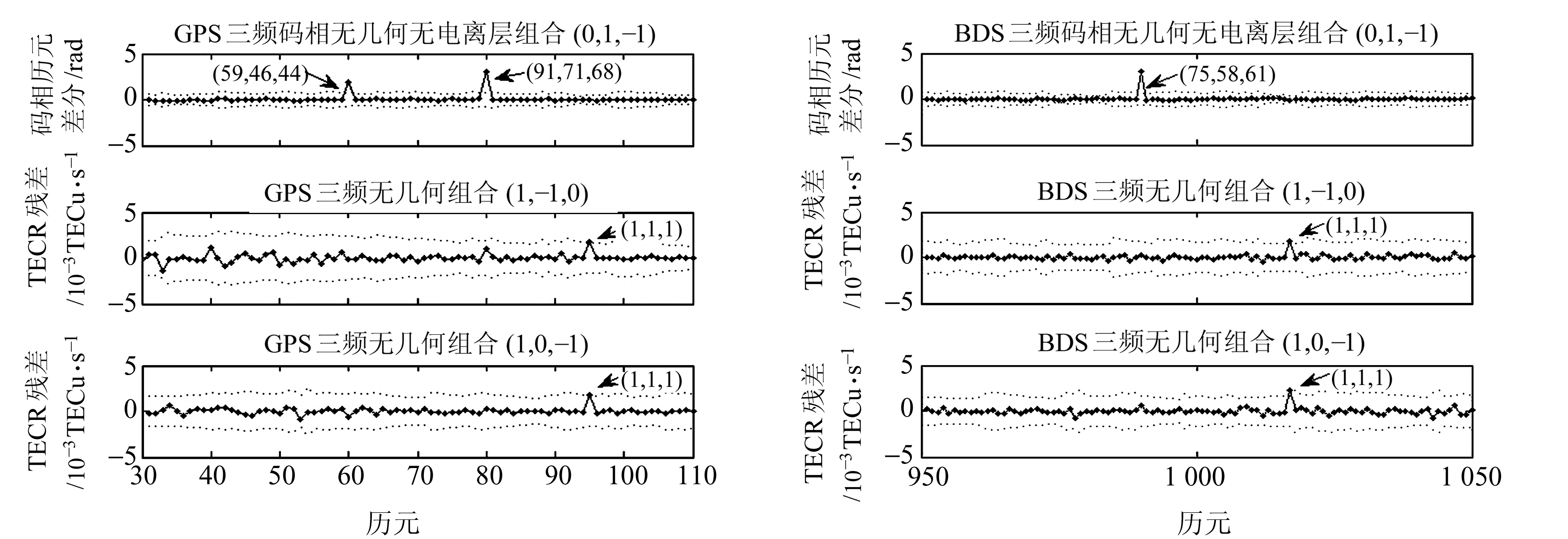
图 2给出了本文算法及阈值结果。可以看见,本文算法能有效削弱电离层影响,使电离层速率残差在零值附近稳定波动,有利于周跳,且阈值设定方法更符合数据的实际波动情况,可防止误探和漏探,提高探测精度。图 3为在电离层变化剧烈的观测时段设置不敏感周跳的探测情况,对三频TECR的不敏感周跳组合((59, 46, 44)、(91, 71, 68)(GPS)和(75, 58, 61)(BDS))、三频码相无几何无电离层组合表现出良好的探测效果。而三频码相无几何无电离层组合无法探测的等周小周跳(1, 1, 1),采用三频TECR组合进行探测,发现其探测量明显高出阈值,故对此类等周周跳可利用三频TECR组合进行补充探测。三频TECR算法与三频码相无几何无电离层组合能有效探测到相互的不敏感周跳组合,消除不敏感组合对周跳探测的影响,提高探测准确性。
|
图 2 削弱电离层延迟的三频TECR算法及其阈值 Fig. 2 Three-frequency TECR algorithm of whittling ionospheric delay and the threshold |
|
图 3 不敏感周跳探测 Fig. 3 The detection of insensitive cycle-slip |
利用载波观测数据的高精度优势,对电离层速率求拟合残差得到最优拟合历元数,完成三频TECR组合对电离层的削弱以及两种方法的阈值求取。本文仅给出GPS和BDS系统[1, -1, 0]的最优拟合历元数的求取情况,如图 4所示。可以看出,最优拟合历元数分布均匀,说明搜索范围[6, 15]是合理的,最小标准差与所选数据段波动一致,表明该算法能快速找到数据段最优数据进行拟合。

|
图 4 最优拟合历元数 Fig. 4 The optimal fitting epochs |
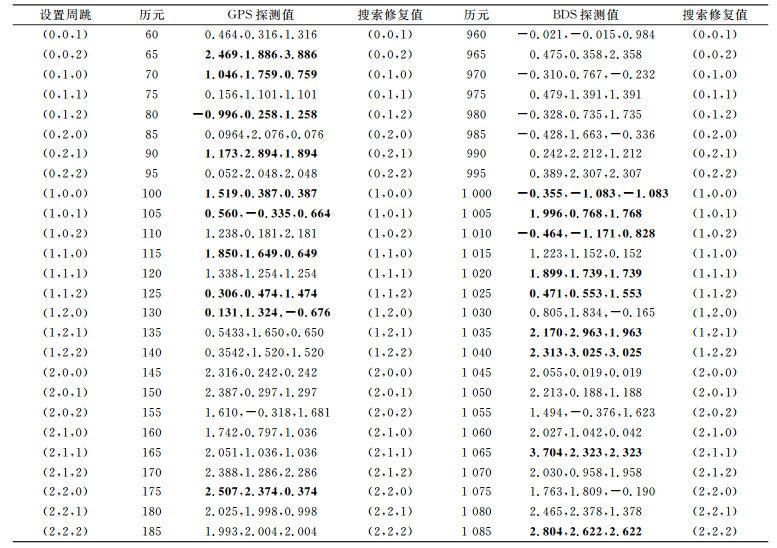
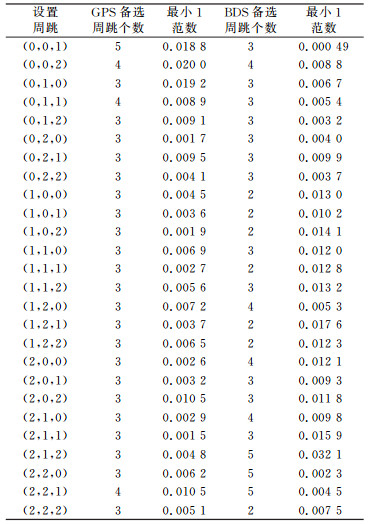
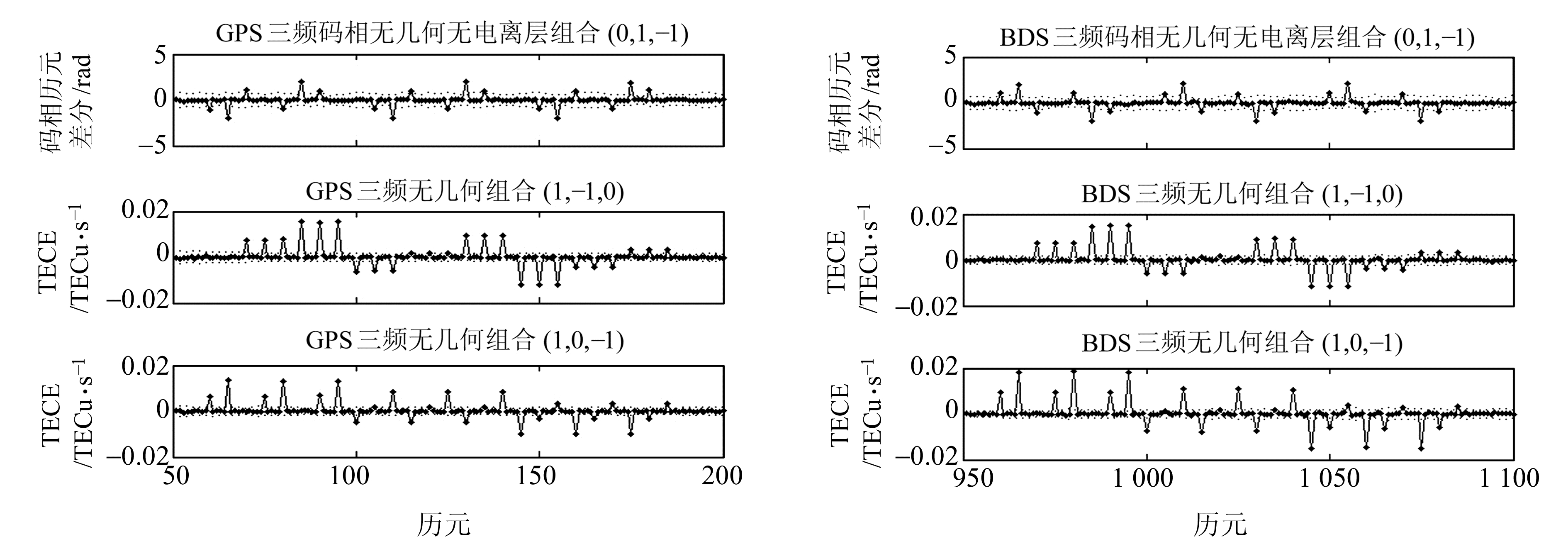
为验证算法的有效性,在上述电离层活动剧烈波段(GPS的30~110历元,BDS的950~1050历元)依次加入(0, 0, 0)~(2, 2, 2)的小周跳,具体探测与修复情况如图 5和表 3所示。从图 5可知,削弱电离层延迟的三频TECR算法能探测到所有小周跳,GPS与BDS的三频TECR组合[1, -1, 0]和[1, 0, -1]噪声较小,削弱电离层影响后在[-0.02, 0.02]间波动,且阈值较合理。从表 3可知,所有小周跳均修复正确,利用式(16)进行修复时,绝大部分周跳可直接取整固定,但舍入误差较大;少数周跳修复不正确(表 3黑体),主要受观测噪声影响,但修复错误值与正确值相差较小,因此需要在小范围内搜索,得到满足式(15)的备选周跳组合,并通过最小1范数确定正确周跳值。具体搜索的备选周跳个数与正确值对应的最小1范数如表 4所示。
|
图 5 连续周跳探测 Fig. 5 Continuous cycle-slip detection |
|
|
表 3 连续小周跳的探测结果 Tab. 3 The result of continuous cycle-slip detection |
|
|
表 4 连续周跳的备选周跳个数及正确周跳的最小1范数 Tab. 4 The number of candidate cycle-slip and 1 minimum norm of correct cycle-clip |
1) 将双频TECR周跳探测算法运用到三频,并与三频码相无几何无电离层组合联合,对不敏感周跳进行互补探测,实现电离层活跃期所有三频小周跳的探测。
2) 通过数据质量分析可快速找到质量最好的数据段,利用此数据段拟合得到最优电离层速率拟合值,并与电离层速率真实值作差,可有效削弱电离层延迟对周跳探测的影响。
3) 根据最优拟合历元数对阈值进行了改进,能避免质量较差数据对阈值的影响,并合理地反映数据动态变化,提高探测精度。
4) 对探测出的周跳进行小范围搜索,利用最小1范数对周跳进行确认,可显著提高周跳修复准确性。
| [1] |
Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophys Res Lett, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [2] |
王泽民, 刘景斌. 卫星定位系统相位组合观测值的模型研究[J]. 武汉大学学报:信息科学版, 2006, 28(6): 723-727 (Wang Zemin, Liu Jingbin. Model of Inter-Frequency Combinations of Galileo GNSS[J]. Geomatics and Information Science of Wuhan University, 2006, 28(6): 723-727)
(  0) 0) |
| [3] |
黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717-725 (Huang Lingyong, Zhai Guojun, Ouyang Yongzhong, et al. Ionospheric Cycle Slip Processing in Triple-frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717-725)
(  0) 0) |
| [4] |
王华润, 柴洪洲, 谢凯. 北斗三频无几何、消电离层组合周跳探测方法研究[J]. 大地测量与地球动力学, 2015, 35(3): 406-411 (Wang Huarun, Chai Hongzhou, Xie Kai. Study of Cycle-Slip Using BDS Triple-Frequency Geometry-Free and Ionosphere-Free Combination[J]. Juournal of Geodesy and Geodynamics, 2015, 35(3): 406-411)
(  0) 0) |
| [5] |
李金龙, 杨元喜, 徐君毅, 等. 基于伪距相位组合实时探测与修复三频GNSS非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717-722 (Li Jinlong, Yang Yuanxi, Xu Junyi, et al. Real-Time Cycle-Slip Detection and Repair Based on Code-Phase Combinations for GNSS Triple-Frequency Undifferenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717-722)
(  0) 0) |
| [6] |
Zhao Q L, Sun B Z, Dai Z Q, et al. Real-Time Detection and Repair of Cycle Slips in Triple-Frequency GNSS Measurements[J]. GPS Solut, 2015, 19(3): 381-391 DOI:10.1007/s10291-014-0396-2
(  0) 0) |
| [7] |
曹新运, 王坚. GPS三频非差观测值探测与修复周跳[J]. 武汉大学学报:信息科学版, 2014, 39(4): 450-456 (Cao Xinyun, Wang Jian. Cycle-Slip Detection and Repair Using GPS Triple-Frequency Un-Different Observations[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 450-456)
(  0) 0) |
| [8] |
Conker R S, Ei-Arini M B, Hegarty C J, et al. Modeling the Effects of Ionospepheric Scintillation on GPS/Satellite-Based Augmentation System Availability[J]. Radio Science, 2001, 38(1): 1 001-1 009
(  0) 0) |
| [9] |
Banville S, Langley R B. Mitigating the Impact of Ionspheric Cycle-Slips in GNSS Observations[J]. Journal of Geodesy, 2013, 87(2): 179-193 DOI:10.1007/s00190-012-0604-1
(  0) 0) |
| [10] |
Cai C S, Liu Z Z, Xia P F, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Inospheric Activity[J]. GPS Solut, 2013, 17(2): 247-260 DOI:10.1007/s10291-012-0275-7
(  0) 0) |
| [11] |
Liu Z Z. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-Frequency GPS Receiver[J]. J Geod, 2011, 85(3): 171-183 DOI:10.1007/s00190-010-0426-y
(  0) 0) |
| [12] |
Teunissen P J G, Bakker P F D. Single-Receiver Sigle-Shannel Multi-Frequency GNSS Integrity: Outliers, Slips and Ionospheric Disturbances[J]. Journal of Geodesy, 2013, 87(2): 161-177 DOI:10.1007/s00190-012-0588-x
(  0) 0) |
| [13] |
黄令勇, 翟国君, 欧阳永忠, 等. 削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840-847 (Huang Lingyong, Zhai Guojun, Ouyang Yongzhong, et al. Triple-Frequency TurboEdit Cycle-slip Processing Method of Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840-847)
(  0) 0) |
| [14] |
李林阳, 吕志平, 崔阳, 等. 伪距相位和无几何相位组合探测与修复多频周跳的分析与比较[J]. 大地测量与地球动力学, 2015, 35(3): 396-400 (Li Linyang, Lü Zhiping, Cui Yang, et al. Analysis and Comparison of Cycle Slip Detection and Repair of Multiple-Frequency Based on Code-Phase and Geometry-Free Combination[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 396-400)
(  0) 0) |
| [15] |
Jin R, Jin S G, Tao X L. Ionspheric Anomalies during the March 2013 Geomagnetic Storm from Beidou Navigation Satellite System(BDS) Observations[C]. China Satellite Navigation Conference, Nanjing, 2014
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37