确定星座中每颗卫星与哪几颗卫星建立链路是导航星座链路拓扑设计要解决的问题。星间链路拓扑决定了整个系统的顶层方案,且影响了自主导航的精度[1-2]。
美国从20世纪80年代就开始对基于星间链路的自主导航进行研究, 并于1998年发射了第一颗安装有UHF(ultra high frequency)频段星间链路的GPS ⅡR卫星[3]。2010年开始发射的GPS ⅡF系列卫星又进一步改进了星间链路功能[4]。目前,GPS Ⅲ卫星计划增加Ka频段星间链路,实现“连接一颗卫星即连接整个星座”的现代化运行模式[5]。俄罗斯在2011年首次发射的新一代导航卫星GLONASS-K上也安装了星间链路收发设备[6]。欧洲航天局正在全面开展Galileo星间链路各项技术研究,并已初步形成几种可选设计方案[7-9]。我国也在积极发展星间链路,并于2015-03成功发射第一颗具备星间链路功能的新一代北斗导航卫星。此外,对于星间链路的建立,国内众多学者相继进行一系列研究工作。范丽等[10]介绍Walker星座星间链路分析设计流程,并提出星间链路的构建准则及优化设计;耿亮等[11]探讨几种经典的星座设计方法,并给出关于星座设计的一些参考;张涛等[12]对最短路径算法进行研究;何家富等[13]提出Walker星座的K短路径算法;周建华等[14]提出一种新的考虑波束限制的星间链路优化方案。
我国北斗二代卫星导航系统的星间链路尚在设计验证阶段,故对导航星座星间链路构型进行研究具有重要意义。保证导航卫星自主导航精度是星间链路构型设计的重要参考指标,本文将以北斗系统仿真星座为对象分别对UHF波段星间链路与Ka波段星间链路的建链数量及PDOP(position dilution of precision)值进行分析,在此基础上,利用不同链路构型下的仿真观测值实现60 d自主导航,探讨星间链路测距模式及星间链路构型对自主导航精度的影响,以期得出有益结论,为北斗二代卫星导航系统星间链路的建立提供参考。
1 星间链路构型 1.1 星间链路的建立目前星间测距主要采用无线电测距模式,主要包括UHF波段测距模式、Ka波段测距模式及S波段测距模式3种。本文将以这3类卫星为对象分别对UHF波段及Ka波段星间链路测距模式进行探讨。
1) UHF波段测距模式
在UHF波段星间链路测距模式下,星间链路采用时分多址(TDMA)方式建立。在该模式下,星间链路建立需考虑以下3个可视条件:地球、电离层及对流层的遮挡,卫星发射天线覆盖范围,信号传播最大距离。
2) Ka波段测距模式
在Ka波段测距模式下,所有卫星将按照星间链路建链方案建立动态切换链路。针对不同的链路需求及建链条件,可以设计不同的动态链路建链方案。所有卫星完成一个周期的星间测距时间为一个时间片,各链路按时序依次建立。时隙为3 s,前1.5 s建立正向链路,后1.5 s建立反向链路,以保证形成双向链路。
1.2 星间链路性能分析由于本文主要探讨星间链路构型对自主导航精度的影响,星间链路构型设计的指标中仅链路数和PDOP值与自主导航精度有关,故主要针对这两项指标,对3GEO/3IGSO/24MEO混合星座的星间链路性能进行分析。其中3颗GEO卫星的定点经度为80.0°、110.5°及140.0°,其与IGSO卫星的轨道根数见表 1;MEO卫星星座为轨道高度21 520 km、倾角55°的Walker24/3/2星座。
|
|
表 1 高轨卫星GEO及IGSO卫星轨道根数值 Tab. 1 Orbital elements of GEO and IGSO |
1) UHF波段测距模式
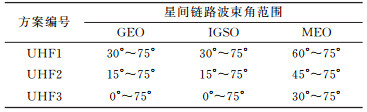
本文针对链路波束角范围的不同设计了几种方案(表 2)。由于仿真星座运动具有极强的周期性,故仅对其单天结果进行分析,历元采样间隔为300 s。
|
|
表 2 UHF波段星间链路方案描述 Tab. 2 Cases of the UHF inter-satellite cross-links |
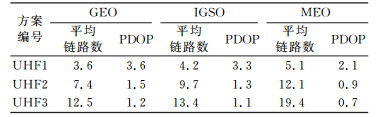
表 3给出了GEO、IGSO及MEO 3类卫星在3种不同波束角范围下的平均链路数和PDOP值。可以看出,随着波束角范围的增大,GEO卫星的平均链路数从3.6增加至12.5,PDOP值也相应从3.6减小至1.2;IGSO卫星的平均链路数从4.2增大至13.4,PDOP值从3.3减小至1.1;MEO卫星的平均链路数则从5.1增大至19.4,PDOP值从2.1减小至0.7。由此可见,波束角的增大能有效增加3类卫星的可建链数量,且能在一定程度上改进3类卫星的星间观测图形结构。
|
|
表 3 UHF波段测距模式下3类卫星平均星间链路数及PDOP值统计 Tab. 3 Statistics of PDOP and mean number of the UHF inter-satellite cross-links |
2) Ka波段测距模式
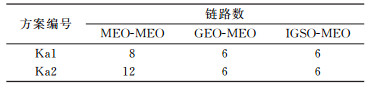
本文设计了两种Ka波段星间动态链路建链方案,见表 4所示。其历元采样间隔同样为300 s,由于卫星运动的周期性,此处同样仅对单天结果进行分析。
|
|
表 4 Ka波段星间链路方案描述 Tab. 4 Cases of the Ka inter-satellite cross-links |
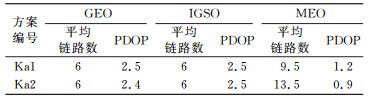
表 5给出了GEO、IGSO及MEO 3类卫星在两种不同Ka波段建链方案下的平均链路数及PDOP值。可以看出,在两类建链方案下,GEO与IGSO的平均链路数均为6条,其PDOP值均约为2.5左右;在Ka1方案下,MEO的平均链路数为9.5,PDOP值为1.2;在Ka2方案下,MEO的平均链路数为13.5,PDOP值约为0.9。MEO的平均链路数后者比前者多4条。该结果显示,在Ka波段测距模式下,实际建链数与建链方案的设计链路数一致,且链路数越多,其PDOP值越小,星间观测图形结构越好。此外,采用Ka波段在星间建立动态切换链路,可通过设计使星间链路更好地满足链路构型的各项指标,应用起来更具灵活性。
|
|
表 5 Ka波段测距模式下3类卫星平均星间链路数及PDOP值统计 Tab. 5 Statistics of PDOP and mean number of the Ka inter-satellite cross-links |
为了分析不同的星间链路构型对自主导航结果的影响,本文将针对不同的星间链路构型方案,分别采用其对应观测数据进行60 d自主导航解算,通过对解算结果精度的分析探讨星间链路构型对自主导航结果的影响。
2.1 仿真观测值的生成由于本文以北斗仿真星座为研究对象,故在进行自主导航计算分析时采用的是星间仿真观测值。其生成过程为:先采用表 1所示开普勒根数,利用STK软件生成仿真星座的精密初始状态值;然后利用卫星初始状态值,采用轨道积分生成仿真精密星历;最后再利用自主研制的观测值仿真软件生成星间仿真伪距观测值。
利用轨道积分生成仿真精密星历的过程中,地球引力模型采用EGM96(20×20),太阳光压模型采用ROCK42模型,考虑日月引力、固体潮、海潮及相对论效应。精密星历中的卫星钟差部分通过IGS发布的CLK文件中GPS Block ⅡA卫星精密钟差信息填补。为了使仿真数据更接近真实,本文在轨道解算所用光压参数初值中人为加入了20%的误差。观测值仿真软件采用自编软件,其按照一定的星间链路测距体制,利用精密星历信息且结合链路拓扑构型原则计算建链卫星间真实几何距离,并在其中加入各类仿真误差从而生成星间仿真观测值。仿真观测值中的误差主要考虑观测粗差、观测噪声、卫星钟差、相对论效应及经过模型改正后的各类残余系统误差,如信号收发硬件延迟、多路径效应等。本文在计算过程中加入的观测噪声为10 cm,加入的残余系统误差固定项为8 cm、周期项为5 cm。自主导航解算策略如表 6所示,采用表 6所示模型对仿真星座轨道进行预报,当预报天数为10 d时,其URE达到5 m;预报天数为60 d时,其URE将达到642 m。
|
|
表 6 自主导航解算策略 Tab. 6 Calculating strategy of auto-navigation |
分别针对UHF波段及Ka波段星间链路进行自主导航仿真计算,星间链路构型的方案描述分别如表 2和表 4所示。
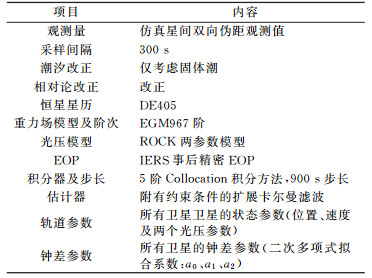
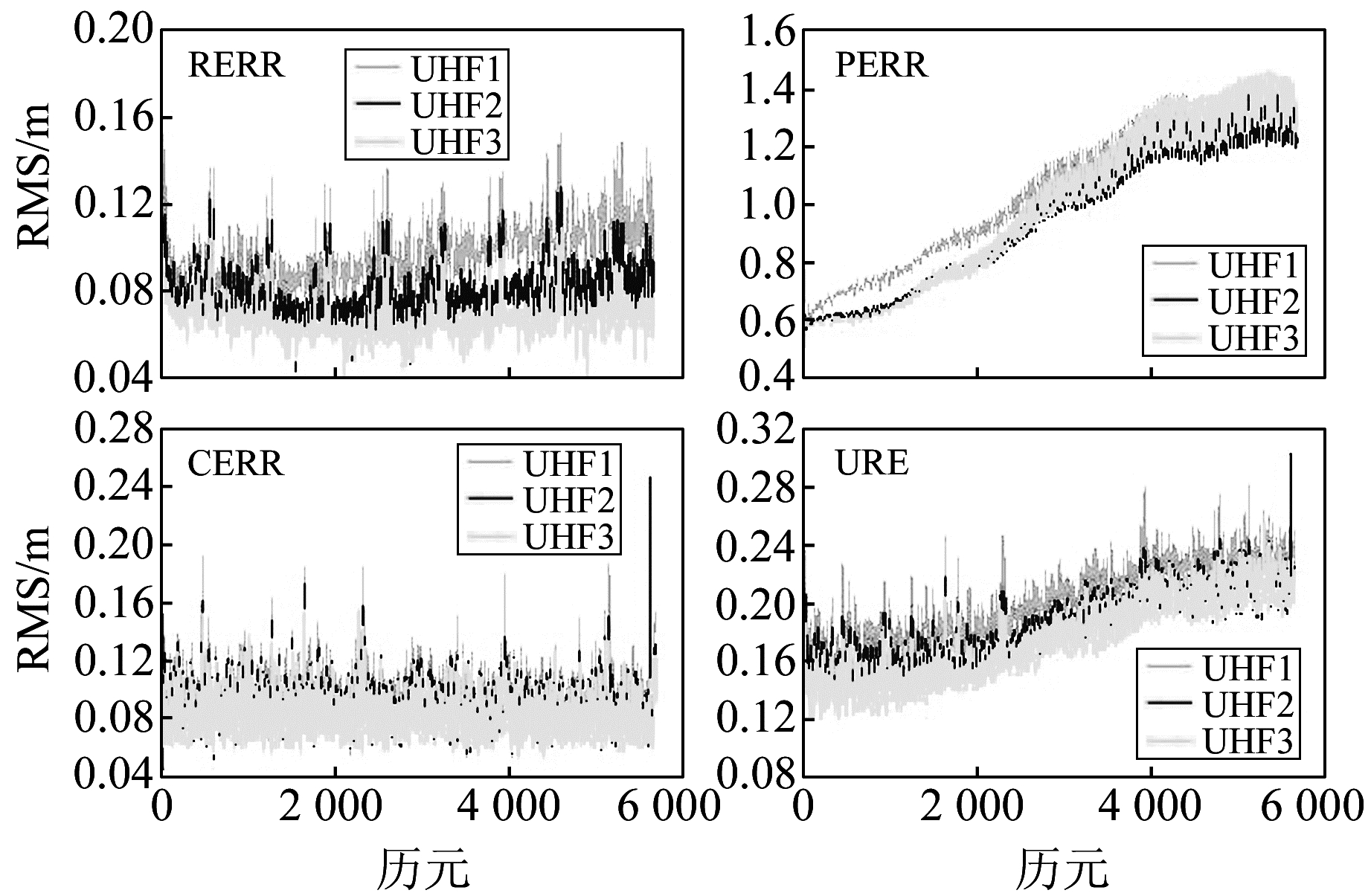
图 1与图 2分别给出了不同UHF波段及Ka波段观测链路情况下60 d自主导航的全星座平均RMS偏差历元时序。为了更好地反映结果变化趋势,图中省略了滤波收敛前的部分历元结果。其中,RERR、PERR、CERR及URE分别表示径向误差、水平方向误差、相对钟差投影至距离的误差及用户距离误差,其解算公式可参照文献[15]。
|
图 1 不同UHF波段观测链路结构情况下60 d自主定轨星座RMS统计结果历元时序 Fig. 1 Time series of RMS of 60 days' auto-navigation calculation in different cases of UHF cross-link structure |

|
图 2 不同Ka波段观测链路结构情况下60 d自主定轨星座RMS统计结果历元时序 Fig. 2 Time series of RMS of 60 days' auto-navigation calculation in different cases of Ka cross-link structure |
从图 1可以看出,采用UHF波段仿真观测值进行60 d自主导航,PERR及URE结果精度随时间逐渐降低,RERR与CERR结果随时间无明显变化趋势;随着波束角范围的增大,自主导航精度有一定的提高,且RERR结果精度改善最为显著;自主导航60 d,UHF1、UHF2及UHF3 3种方案下的URE结果分别约为0.25 m、0.22 m及0.21 m。
从图 2可以看出,采用Ka波段仿真观测值进行60 d自主导航,4类参量结果变化规律与图 1一致。虽然Ka2方案的MEO星间链路数较Ka1方案多了4条,但两类方案其GEO、IGSO卫星与MEO卫星间的星间链路数相同,故这两类方案情况下的自主导航精度相当,无明显差距。自主导航第60 d,Ka1与Ka2两种方案下的URE结果分别约为0.24 m及0.23 m。
对比UHF波段与Ka波段自主导航结果可以看出,由于Ka波段两种方案的PDOP值介于UHF1与UHF3方案之间,故前者自主导航结果与UHF2方案自主导航结果接近。总体而言,两类测距模式的自主导航精度相当,自主导航60 d其结果误差均约为0.2 m。但在不同的建链方案下,随着链路数的增加及观测结构的改善(PDOP值的减小),自主导航精度有一定程度的改善,改善量级为cm级。
3 结语本文以北斗仿真星座为对象,分别探讨了UHF波段及Ka波段两种测距模式的不同星间链路建链条件下GEO、IGSO及MEO卫星的可建链路数及PDOP值的变化。此外,还针对不同星间链路构型方案,分别采用其对应仿真观测数据进行了60 d自主导航解算,通过对解算结果精度的分析,探讨了星间链路测距模式及星间链路构型对自主导航的影响。通过研究可得出以下结论。
1) 在UHF波段测距模式下,波束角的增大能有效增加3类卫星的可建链数量,且其能在一定程度上改进3类卫星的星间观测图形结构;在Ka波段测距模式下,实际建链数与建链方案的设计链路数一致,且链路数越多,其PDOP值越小,星间观测图形结构越好。采用Ka波段在星间建立动态切换链路,可通过设计使星间链路更好地满足链路构型的各项指标,应用起来更具灵活性。
2) 自主导航精度与星间链路测距模式无关。改善链路条件在一定程度上能提高自主导航精度,但其提高程度有限,最大影响量级为cm级。当链路条件改善到一定程度后,进一步对其进行改善对提高自主导航精度作用不大。
因此,星间链路测距模式对自主导航精度无影响,而星间链路构型则对自主导航精度存在一定的影响。在星间链路设计过程中应综合考虑导航精度、链路负荷及建设成本等因素,以达到最优效果。
| [1] |
刘万科.导航卫星自主定轨及星地联合定轨的方法研究及模拟计算[D].武汉: 武汉大学, 2008 (Liu Wanke. Method and Simulation of Autonomous Orbit Determination and Combined Orbit Determination for Navigation Satellites[D]. Wuhan: Wuhan University, 2008)
(  0) 0) |
| [2] |
李振东, 何善宝, 刘崇华, 等. 一种导航星座星间链路拓扑设计方法[J]. 航天器工程, 2011, 20(3): 32-37 (Li Zhendong, He Shanbao, Liu Chonghua, et al. An Toplogy Design Method of Navigation Satellite Constellation Inter-Satellite Links[J]. Spacecraft Engineering, 2011, 20(3): 32-37 DOI:10.3969/j.issn.1673-8748.2011.03.005)
(  0) 0) |
| [3] |
Codik A. Autonomous Navigation of GPS Satellites:A Challenge for the Future[J]. Navigation, 1985, 32(3): 221-232 DOI:10.1002/navi.1985.32.issue-3
(  0) 0) |
| [4] |
李龙龙, 耿国桐, 李作虎. 国外卫星导航系统星间链路发展研究[J]. 测绘科学技术学报, 2016, 33(2): 133-138 (Li Longlong, Geng Guotong, Li Zuohu. Study of Development of the Inter-Satellite Links in Foreign GNSS[J]. Journal of Geomatics Science and Technology, 2016, 33(2): 133-138)
(  0) 0) |
| [5] |
Luba O, Boyd L, Gower A, et al. GPS Ⅲ System Operations Concepts[J]. Aerospace and Electronic Systems Magazine, IEEE, 2005, 20(1): 10-18 DOI:10.1109/MAES.2005.1396789
(  0) 0) |
| [6] |
林益明, 何善宝, 郑晋军, 等. 全球导航星座星间链路技术发展建议[J]. 航天器工程, 2010, 19(6): 1-7 (Lin Yiming, He Shanbao, Zheng Jinjun, et al. Development Recommendation of Inter-Satellite Links in GNSS[J]. Spacecraft Engineering, 2010, 19(6): 1-7 DOI:10.3969/j.issn.1673-8748.2010.06.001)
(  0) 0) |
| [7] |
Fernander F A. Inter-Satellite Ranging and Inter-Satellite Communication Links for Enhancing GNSS Satellite Broadcast Navigation Data[J]. Advances in Space Research, 2011, 47(5): 786-801 DOI:10.1016/j.asr.2010.10.002
(  0) 0) |
| [8] |
Sanchez M, Pulido J A, Amarillo F, et al. Inter-Satellite Ranging and Communication Links in the Frame of the GNSS Infrastructure Evolution[C]. 21st International Technical Meeting of the Satellite Division of The Institute of Navigation(ION GNSS 2008), Savannah, 2008
(  0) 0) |
| [9] |
D'Angelo P, Fernander A, Cuardabrazo T, et al. Enhancement of GNSS Navigation Function by the Use of Inter-Satellite Links[C]. 2012 6th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing(NAVITEC), Noordwijk, 2012 https://www.researchgate.net/publication/261164137_enhancement_of_gnss_navigation_function_by_the_use_of_inter-satellite_links
(  0) 0) |
| [10] |
范丽, 张育林. 区域覆盖混合星座设计[J]. 航天控制, 2007, 25(6): 52-55 (Fan Li, Zhang Yulin. Regional Coverage Hybrid Constellation Design[J]. Aerospace Control, 2007, 25(6): 52-55 DOI:10.3969/j.issn.1006-3242.2007.06.010)
(  0) 0) |
| [11] |
耿亮, 吴诗其. 星座设计与星间链路的建立[J]. 中国空间科学技术, 2000, 20(6): 62-67 (Geng Liang, Wu Shiqi. Constellations Design and Establishment of the Inter-Satellite Links[J]. Chinese Space Science and Technology, 2000, 20(6): 62-67 DOI:10.3321/j.issn:1000-758X.2000.06.010)
(  0) 0) |
| [12] |
张涛, 刘重堪. 卫星时变网络拓扑最短路径算法研究[J]. 计算机学报, 2006, 29(3): 371-377 (Zhang Tao, Liu Chongkan. A Shortest Path Algorithm for Satellite Time-Varying Topological Network[J]. Chinese Journal of Computers, 2006, 29(3): 371-377 DOI:10.3321/j.issn:0254-4164.2006.03.003)
(  0) 0) |
| [13] |
何家富, 姜勇, 张更新, 等. 一种具有异轨星间链路的Walker星座网络拓扑与路由生成方案[J]. 解放军理工大学学报:自然科学版, 2009, 10(5): 409-413 (He Jiafu, Jiang Yong, Zhang Gengxin, et al. Topology and Route Production Scenario of Walker Satellite Constellation Network with Inter-Satellite Links[J]. Journal of PLA University of Science and Technology(Nature Science Edition), 2009, 10(5): 409-413)
(  0) 0) |
| [14] |
周建华, 杨龙, 徐波, 等. 考虑波束限制的改进导航星座星间链路方案[J]. 中国科学:物理学力学天文学, 2011, 41(5): 575-580 (Zhou Jianhua, Yang Long, Xu Bo, et al. An Improved Satellite Link Scheme with Beam Restriction for the Navigation Constellation[J]. Scientia Sinica Phys, Mech & Astron, 2011, 41(5): 575-580)
(  0) 0) |
| [15] |
Ananda M P, Bernstein H, Cunningham K E, et al. Global Positioning System Autonomous Navigation[J]. IEEE Position Location & Navigation Symposium, 1990, 27(1): 497-508
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37