2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054
我国航天事业迅猛发展,航天活动日益频繁,在轨航天器数量将在2020年超过200颗,占全球总量的20%,最具代表性的成就是北斗系统和载人航天[1]。
航天器执行任务时需要确定其轨道信息,同时,为保证任务载荷工作环境,也需要深刻认识、精确控制航天器轨道特性。例如,低轨道航天器受到复杂的大气阻力,需对其长半轴定期调整以补偿由大气阻力导致的轨道衰减[2];地球同步轨道卫星则需通过位置控制以抵消日、地、月等摄动力影响。再者,在轨和废弃航天器数目越来越庞大,精密轨道确定和预报对空间碰撞预警也至关重要[3]。
不同航天器受到的摄动力各不相同,在大小和方向上都很复杂,需针对轨道特点分别探讨。本文以轨道高度为分类依据,对我国低轨道、中轨道和高轨道航天器分别进行分析。首先总结轨道摄动力模型和轨道预报方法,详细给出轨道预报策略;然后深入阐述初始轨道获取方法和摄动力模型参数选择;在此基础上,针对不同航天器定量研究不同摄动力对轨道预报的影响。
1 数值积分轨道预报二体问题是航天器实际受摄运动的简化描述,地球引力成为影响航天器运动的唯一力。根据牛顿运动定律,其加速度为[4]:
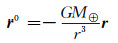
|
(1) |
式中,-r/r表示航天器指向地心的单位矢量,引力常数G=6.672 59×10-11m3kg-1s-2[2],GM⊕是地球质量与引力常数的乘积。根据式(1),可通过初始条件进行二体问题下的轨道预报。
事实上,航天器飞行是复杂受摄运动,高精度轨道预报是根据模型化的各种摄动加速度解算航天器轨道。这里考虑的主要摄动力模型包括地球非球形摄动、潮汐、三体引力摄动、大气阻力摄动、太阳光压摄动、地球辐射压摄动[2, 4-6]。
由航天器的摄动加速度可得其二阶微分运动方程为:
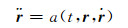
|
(2) |
式中,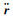
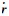
根据文献[4-6],采用嵌套的龙格-库塔(Runge-Kutta-Fehlberg, RKF)数值积分方法求解方程(2),可获得待定时刻航天器位置和速度。
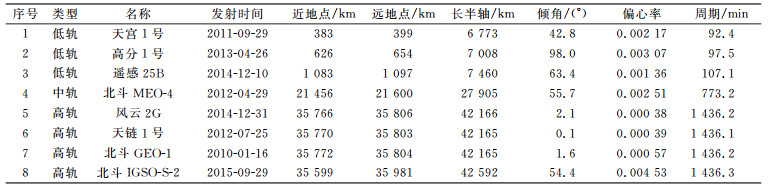
2 实验数据处理 2.1 实验航天器概述与分类低轨道卫星指的是轨道高度在160~2 000 km范围内的卫星,中轨道卫星的轨道高度在2 000~35 786 km,高于35 786 km则为高轨道卫星[7]。以我国在3类轨道上的代表航天器为研究对象,总结不同类型航天器的主要轨道参数,获取某时刻下的初始轨道,根据航天器所受摄动力,采用数值方法进行轨道预报,分析和统计主要摄动力对轨道的影响量级。表 1总结对比了位于低、中、高轨道的8个航天器的主要轨道参数。
|
|
表 1 实验航天器主要轨道参数 Tab. 1 Main orbit parameters of experimental spacecraft |
轨道参数是航天器运动方程求解的必要起算条件。但不同航天器观测方法不同,轨道根数不同,成果基准不同,精度也不在相同数量级上,且难以通过获取原始观测数据的方法进行初轨计算。为了统一所有实验航天器的初始条件,本文采用TLE作为初轨来源,计算航天器在UTC和TEME下的位置和速度[8-9],并转换至J2000惯性坐标系,作为轨道积分初始条件。表 2给出实验航天器在对应参考历元下的初始条件,时间是UTC。
|
|
表 2 航天器初始条件(J2000) Tab. 2 Initial conditions of experimental spacecraft (J2000) |
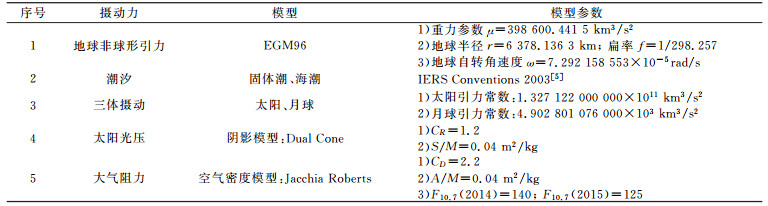
由于航天器制造材料特殊、宇宙环境复杂多变等原因,光压系数、阻尼系数和面质比参数设定较复杂。本文将太阳光压、阻尼系数和面质比等参数设置为典型常数[4],太阳辐射通量F10.7数据由美国国家地球物理数据中心发布。表 3具体描述主要摄动力模型及其参数。
|
|
表 3 摄动力模型 Tab. 3 Perturbation force models |
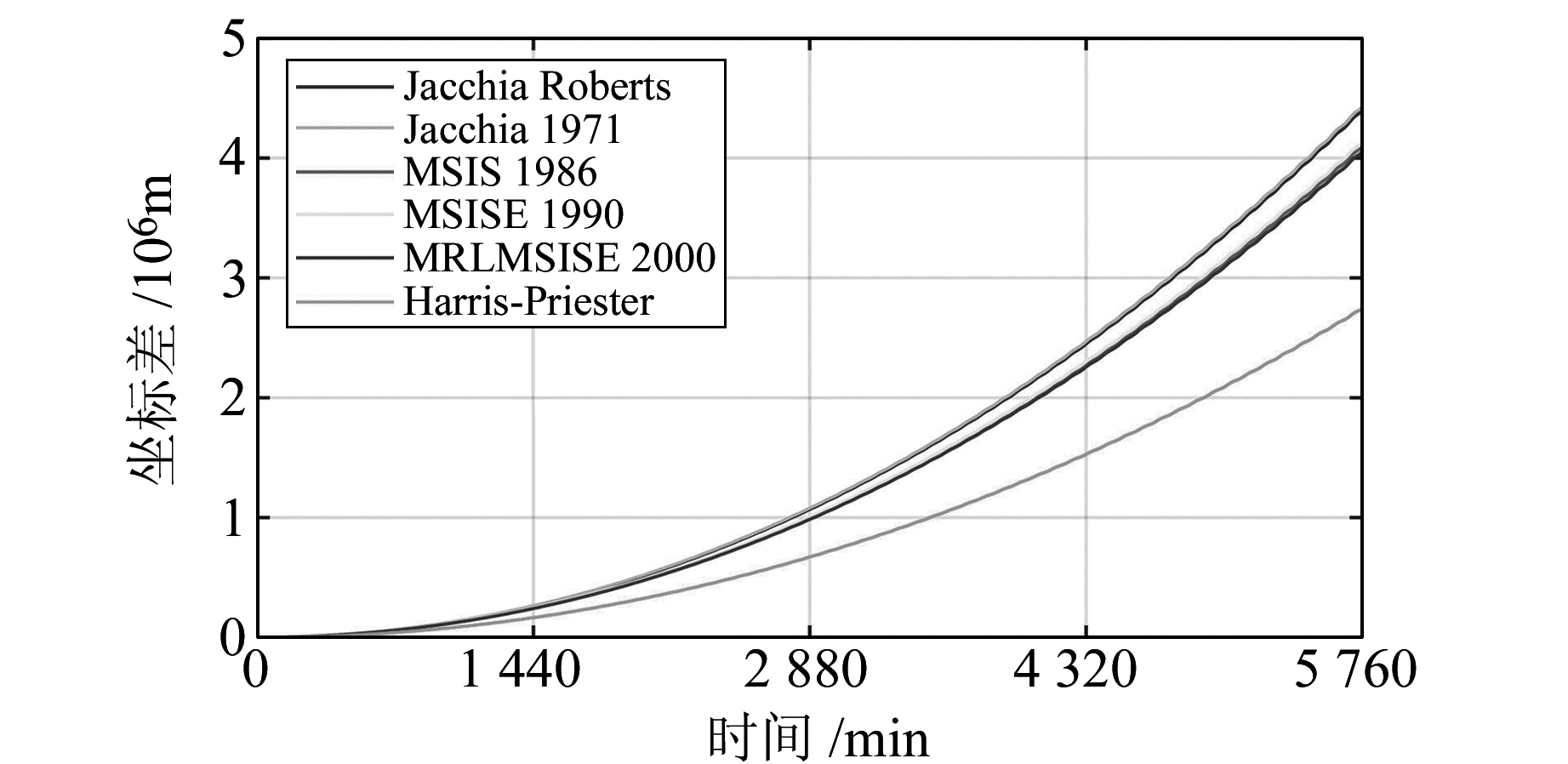
根据文献[2],大气阻力摄动的计算与大气密度模型有关。为了讨论不同大气密度模型的差异,比较了6种常见的大气密度模型,分别是Jacchia系列的Jacchia Roberts与Jaccia 1971,MSIS系列的MSIS 1986、MSISE 1990与NRLMSISE 2000,以及Harrs-Priester。实验采用天宫一号航天器,用二体轨道加一种大气阻力摄动的方式预报4 d轨道,与二体轨道相比获得3 D坐标差,如图 1(初始历元为2016291.0,外推4 d)所示。可以看出,相同系列的大气阻力模型影响量级一致。其中,预报1 d轨道时,3个系列大气密度模型对轨道的影响量级相当。当预报4 d轨道时,最大的影响是Jacchia系列,预报4 d轨道对坐标差的影响量级达4.5×106 m,MSIS系列大气密度模型的影响量级在4.0×106 m,而Harris-Priester模型小于3×106 m。通过分析和比较不同密度模型的表现说明[2, 10],选择中等复杂程度的密度模型是合理的,并且能有效降低计算量和数据存储需求。根据文献[2]提供的不同密度模型的CPU计算时间、平均和最大密度偏差,Jacchia-Roberts模型精度与Jacchia 1971模型相当,而其CPU性能比Jacchia 1971提高了5倍,因此本文选择综合性能较优的Jacchia-Roberts模型作为大气密度模型。
|
图 1 不同大气密度模型对天宫一号空间站轨道的影响 Fig. 1 Affects for different atmosphere density models of Tiangong-1 space station |
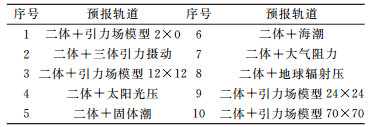
从初始历元开始,根据获取的初始轨道,在各种摄动力下进行积分,预报4 d航天器轨道,积分步长为10 s。为了研究摄动力对轨道影响的量级,本文未预报一个叠加所有摄动力的受摄轨道,而是独立预报每种摄动力下的航天器轨道。如表 4所示(参考轨道:二体问题轨道),每个航天器共有11个预报轨道,包括一个参考轨道(即二体问题轨道),以及10个不同摄动力下的预报轨道。除二体轨道外,其他预报轨道都基于二体问题和某一摄动力。将每个预报轨道与参考轨道求差,得到3个方向的位置坐标差并进行比较。图 2~9给出各航天器摄动力影响结果,其中横轴以min为单位,共5 760 min;纵轴为对数坐标,表示摄动力轨道与二体轨道3D坐标差,单位是m。为了更清晰地表示引力场模型的影响,选取了4种常用的引力场模型(2×0、12×12、24×24和70×70)作为对比。
|
|
表 4 不同摄动力下的预报轨道 Tab. 4 Propagation orbits under different perturbation forces |
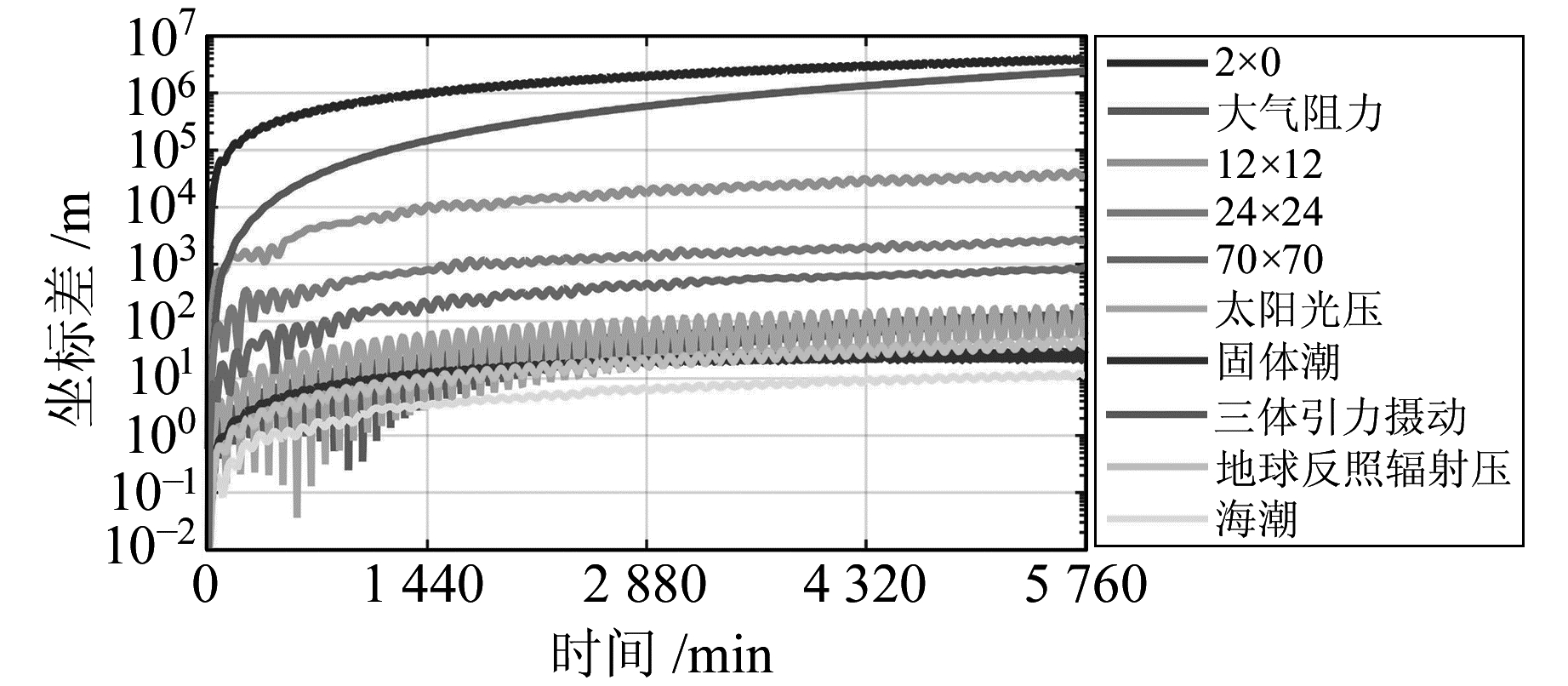
|
图 2 天宫一号空间站轨道摄动力分析 Fig. 2 Analysis of perturbation force for Tiangong-1 space station |

|
图 3 高分一号卫星轨道摄动力分析 Fig. 3 Analysis of perturbation force for Gaofen-1 satellite |

|
图 4 遥感25B卫星轨道摄动力分析 Fig. 4 Analysis of perturbation force for Yaogan-25B satellite |
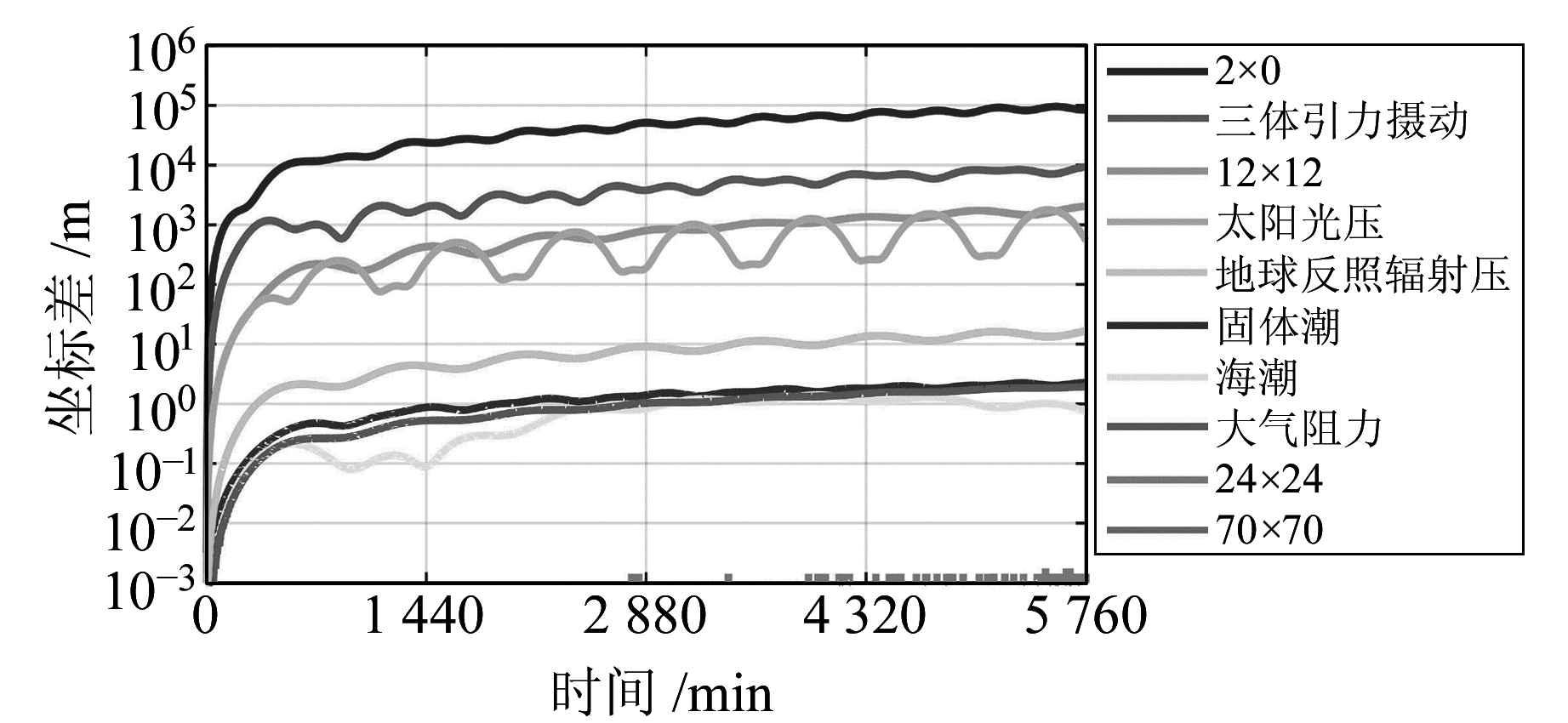
|
图 5 北斗MEO-4卫星轨道摄动力分析 Fig. 5 Analysis of perturbation force for Beidou MEO-4 satellite |

|
图 6 天链1-03号卫星轨道摄动力分析 Fig. 6 Analysis of perturbation force for Tianlian-1-03 satellite |
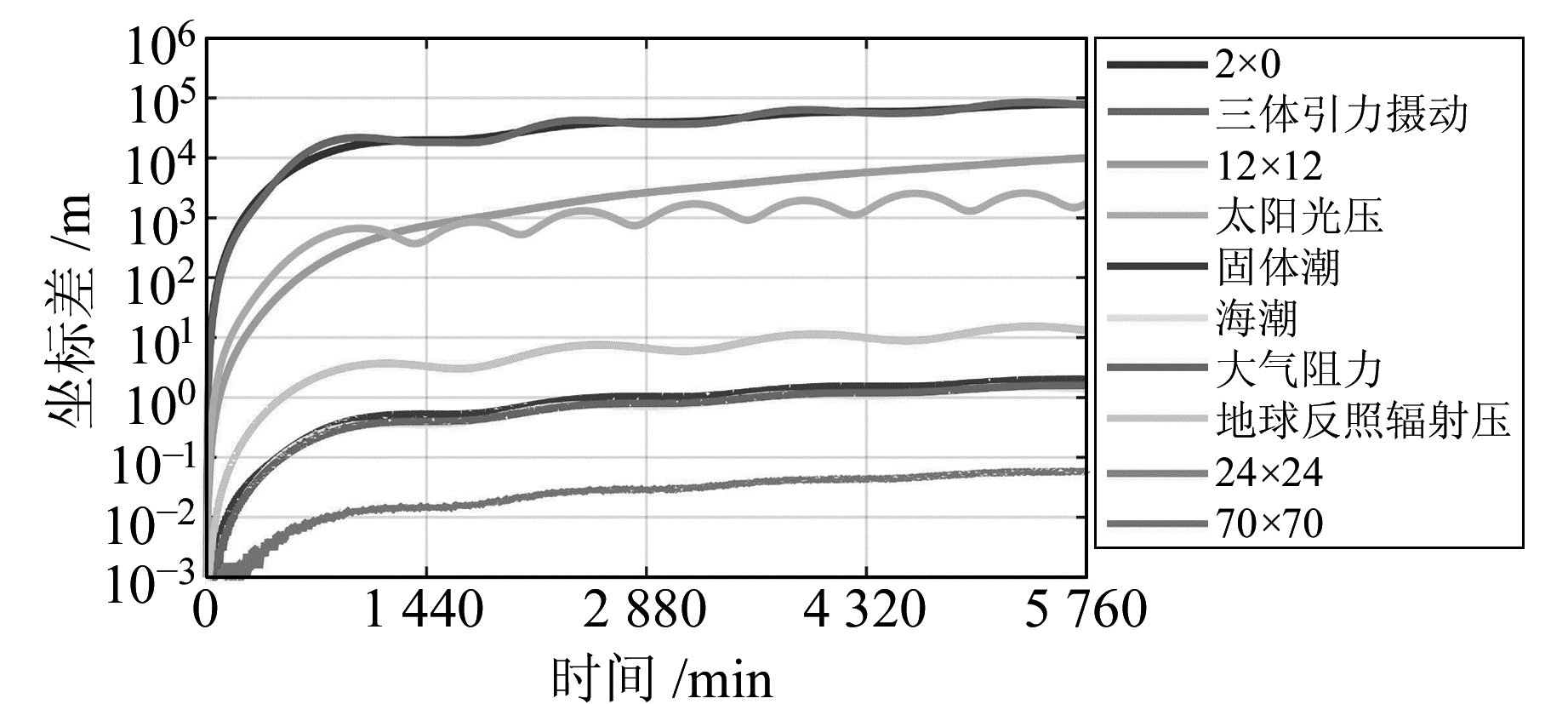
|
图 7 风云2G卫星轨道摄动力分析 Fig. 7 Analysis of perturbation force for Fengyun-2G satellite |

|
图 8 北斗IGSO-S-2卫星轨道摄动力分析 Fig. 8 Analysis of perturbation force for Beidou IGSO-S-2 satellite |
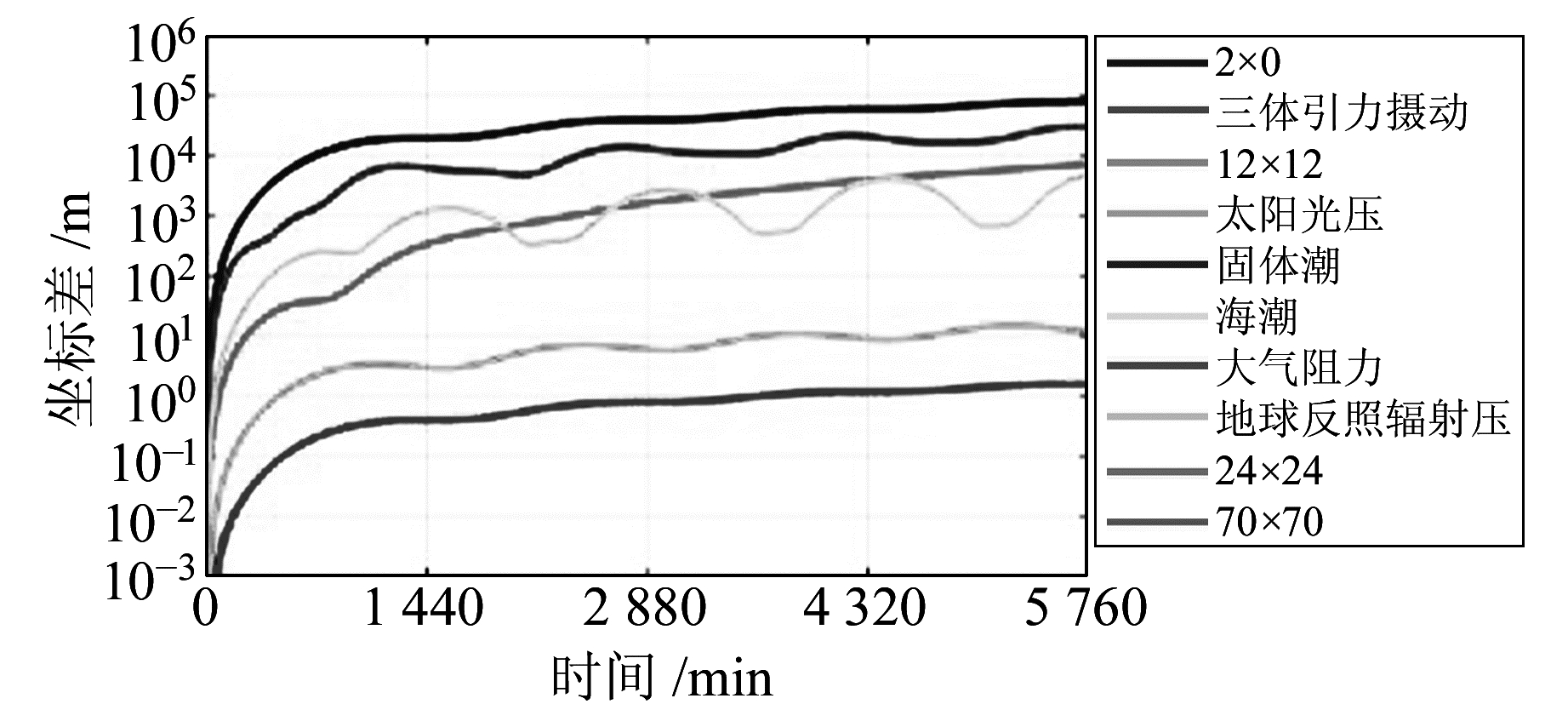
|
图 9 北斗GEO-1卫星轨道摄动力分析 Fig. 9 Analysis of perturbation force for Beidou GEO-1 space station |
实验采用的低轨航天器包括天宫一号空间站、高分一号和遥感25B卫星。
对于天宫一号空间站,按照引起的位置偏移量大小,摄动因素排在前两位的依次为地球非球形引力和大气阻力。其中,地球非球形引力引起的位置偏移量显著,24 h预报时位置偏移量达到106m,显著高于其他摄动因素。当引力场模型阶数增加时,轨道精度随之提高。大气阻力摄动对位置偏移量的影响较地球非球形引力低1个数量级,但是大气阻力引起的位置偏移量非线性增长,是增长最快的摄动力,如图 2(航天器质量为8 500 kg,初始历元为2015-04-23 00:00,预报4 d)所示,预报时间长度每增加24 h,其影响增大一个数量级。因此,对近地航天器而言大气阻力影响尤为显著。
当预报时间大于48 h,太阳光压摄动、三体引力摄动引起的位置偏移量达到100 m,同时表现出强烈的周期性特征且振幅较大。在0~24 h内出现15次波峰,波动周期约为96 min,与天宫一号运行周期(92.4 min)相吻合。导致这种现象的原因可能是天宫一号运行轨道周期性出现在地影时期,使太阳光压产生较大振幅。同样,三体引力摄动也因第三体至天宫一号的距离周期改变而产生周期性变化。当预报时间大于24 h时,固体潮与地球辐射压引起的位置偏移量稳定在10 m左右。
对于高分一号低轨道卫星而言(图 3,卫星质量为1 080 kg,初始历元为2015-01-20 00:00,预报4 d),最大的摄动因素依然是地球非球形引力,其引起的位置偏移量随着预报时间的增加而显著增大,2×0模型在96 h预报时位置偏移量达到107 m。当引力场模型阶数增加时,轨道精度也随之提高。第二个主要的摄动因素依然是大气阻力。由于高分一号轨道较天宫一号高,大气阻力影响比天宫一号小约2个数量级。太阳光压引起的位移偏差量在预报24 h时达到10 m量级,并在后72 h预报中逐渐增长至100 m量级,具有周期性特征,周期约为96 min,与卫星97.5 min的运动周期一致。固体潮与太阳光压的影响数量级相似,比地球辐射压高约三分之一。海潮影响量级最小,在96 h预报过程中,有小振幅周期变化,但数量级基本保持稳定。
与高分一号相比,遥感25B轨道更高(图 4,初始历元为2015-01-20 00:00,预报4 d),其受到的大气阻力比天宫一号低4个数量级。太阳光压引起的位移偏差量增长缓慢,同样表现出强烈周期性特征且振幅较大。在每24 h轨道中出现14个波峰,周期约为103 min,与卫星107.1 min的运动周期相符合。固体潮与地球辐射压处于两个平行量级,分别在预报48 h后稳定于100 m和10 m。在这些摄动力中,海潮影响量级最小。
3.2 中轨道航天器中轨道的代表是北斗MEO卫星,这里对MEO-4进行摄动力分析。
如图 5(卫星质量为1 500 kg,初始历元为2015-04-20 00:00 TLE预报轨道,预报4 d)所示,地球非球形引力是引起位置偏移量最大的摄动因素,然而它的量级比低轨航天器小约1.5个数量级,预报24 h时位置偏移量达到104~105 m。其他摄动影响依次是三体引力摄动、太阳光压、地球反照辐射压、固体潮。在预报大于24 h时,这4种摄动力增长缓慢,量级分别达到103 m、102 m、10 m和1 m,其半天周期特性与卫星周期保持一致(773.2 min)。由于MEO卫星轨道高度在20 000 km以上,大气阻力影响非常小,与海潮处于同一数量级。另外,值得注意的是,引力场阶数增加到24以上时轨道变化不明显。
3.3 高轨道航天器我们选择天链一号、风云2G、北斗IGSO-S-2和GEO-1进行高轨道卫星摄动力分析。
如图 6(卫星质量为2 100 kg,初始历元为2015-01-20 00:00 TLE预报轨道,预报4 d)所示,对于天链一号,按照位置偏移量大小,摄动因素排在前两位的依次是地球非球形引力、三体引力。其中,地球非球形引力引起的位置偏移量显著,24 h预报时位置偏移量达到104 m,显著高于其他摄动因素,但远低于地球非球形引力对低轨道航天器位置偏移量的影响。当引力场模型阶数增加时,轨道精度随之提高,当模型阶数大于24×24后,轨道精度改善有限。当预报时间大于24 h时,太阳光压引起的位置偏移量迅速增加并稳定在1 000 m量级,且周期特征清晰,约为1 d。大气阻力、地球辐射压、固体潮、海潮等摄动引起的位置偏移量较小,小于1 m。
风云2G卫星(图 7,卫星质量为1 380 kg,初始历元为2015-01-20 00:00,预报4 d)由三体引力摄动产生的位置偏移量与2×0地球非球形引力相当,24 h预报时位置偏移量达到104 m,96 h预报时位置偏移量达到105 m。预报时间小于24 h时,太阳光压摄动影响大于12×12地球非球形引力;预报时间大于24 h,12×12地球非球形引力产生的位置偏移量迅速增加;至94 h时,比太阳光压产生的位置偏移量大了约一个数量级。对于高轨道航天器,大气阻力、地球辐射压、固体潮、海潮都是影响非常小的摄动力。
对于北斗IGSO-S-2卫星(图 8,卫星质量为1 500 kg,初始历元为2016-10-17 00:00 TLE预报轨道,预报4 d),按照位置偏移量大小,摄动因素排在前两位的依次是地球非球形引力、三体引力摄动。地球非球形引力摄动产生的位置偏移量最大,达到104 m。太阳光压引起的位置偏移量达103 m内。当预报时间大于24 h时,地球辐射压引起的位置偏移量在1~10 m之间,与风云2G卫星类似。固体潮、海潮和大气阻力摄动影响较小,预报96 h时达到1 m。
北斗GEO-1(图 9,卫星质量为1 500 kg,初始历元为2014-10-02 00:00 TLE预报轨道,预报4 d)的2×0非球形引力场产生的位置偏移量最大,量级上大于IGSO卫星,约为104~105 m;其次是三体引力,预报24 h量级增加到104 m;太阳光压预报24 h偏移量为103 m,以1 440 min为周期,与卫星周期近似;地球辐射压的特征与IGSO卫星相似,量级在1~10 m之间。固体潮、海潮和大气阻力依然是高轨道卫星影响量级最小的摄动力。
4 结语本文详细阐述了航天器轨道积分预报方法和主要摄动力模型。以航天器轨道高度为分类依据,选取我国低、中、高轨道共8个航天器,说明初始轨道获取方法和摄动力模型参数选择;以轨道类型和摄动力为分类依据,独立分析地球非球形引力、三体引力、大气阻力、太阳光压等摄动力对轨道预报精度的影响。结果表明,摄动力与轨道高度、运行周期等因素密切相关,地球非球形引力是产生位置偏移量最大的摄动力,大气阻力随着轨道高度增加影响显著降低,太阳光压表现出强烈的周期性,与航天器运行周期基本一致。
| [1] |
Ge M, Zhang H P, Jia X L, et al. What is Achievable with the Current Compass Constellation?[J]. GPS World, 2012, 331-339
(  0) 0) |
| [2] |
Montenbruck O, Gill E. Satellite Orbits Models, Methods and Applications[J]. Applied Mechanics Reviews, 2000, 55(2): 2 504-2 510
(  0) 0) |
| [3] |
陈磊, 白显宗, 梁彦刚. 空间目标轨道数据应用——碰撞预警与态势分析[M]. 北京: 国防工业出版社, 2015 (Chen Lei, Bai Xianzong, Liang Yangang. Space Target Orbit Data Applications-Collision Warning and Situational Analysis[M]. Beijing: National Defense Industry Press, 2015)
(  0) 0) |
| [4] |
刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000 (Liu Lin. Orbit Theory of Spacecraft[M]. Beijing: National Defense Industry Press, 2000)
(  0) 0) |
| [5] |
Mc Carthy D, Petit G.IERS Technical Note No. 32[C]. IERS Conventions, 2003
(  0) 0) |
| [6] |
刘林. 人造地球卫星轨道力学[M]. 北京: 高等教育出版社, 1992 (Liu Lin. Orbit Mechanics of Artificial Earth Satellite[M]. Beijing: Higher Education Press, 1992)
(  0) 0) |
| [7] | |
| [8] |
Vallado D A, Crawford P, Hujsak R. Revisiting Spacetrack No.3[C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, Colorado, 2006
(  0) 0) |
| [9] |
Vallado D A, Crawford P. SGP4 Orbit Determination[C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, 2008 https://arc.aiaa.org/doi/abs/10.2514/6.2008-6770
(  0) 0) |
| [10] |
Gaposchkin E M, Coster A J. Evaluation of Thermospheric Models and the Precipitation Index for Satellite Drag[J]. Adv Space Res, 1990(10): 3 303-3 309
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37