2. 中国矿业大学江苏省资源环境信息工程重点实验室, 徐州市大学路1号, 221116
某些特殊环境中,由于信号的遮挡,全球定位技术会因可见卫星数量少导致模糊度固定出错或定位精度低甚至不能定位的现象[1-2],而多系统进行组合会大大增加可见卫星的数量。但由于三大导航定位卫星系统的时间定义、坐标系统的实现方式以及卫星的钟差都存在差异,各个系统的卫星高度、轨道倾角、信号频率也有所差异,同时信号在传播的过程中会受到电离层、对流层、多路径效应等误差的影响,多系统组合的精度究竟如何还需进一步论证[3-4]。
本文首先对多系统组合的模型进行介绍,然后通过对亚太地区部分MGEX站的实测数据进行精密单点定位处理,分析出各种系统组合的最大截止高度角。以10°、13°和15°的7种系统组合解算结果的均值作为真值,再通过设定不同的卫星截止高度角和系统组合,求出此类情况的RMS,分析固定截止高度角下最优系统组合以及同一系统组合下最优截止卫星高度角[5]。该结论可以为存在卫星信号遮挡的GNSS测量提供技术指导。文中的G指GPS,R指GLONASS,C指BDS。
1 多系统组合定位模型 1.1 时间系统的统一GPS、GLONASS和BDS 3个系统都采用原子时,但对时间起点的定义以及维持方式均不同,导致3个系统之间除存在整数倍秒长外还存在微小项。由于该微小项需要积分,计算较为复杂,所以在多系统组合时多将3个系统之间的时间差作为参数进行估计[6-7]。3个系统之间时间转化模型为:
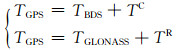
|
式中,TGPS表示GPS时,TGLONASS表示GLONASS时,TBDS表示BDS时,TC表示BDST与GPST之间的偏差,TR表示TGLONASS与TGPS之间的偏差。
1.2 精密单点定位模型通过以上转化可以将时间系统进行统一,统一后的多系统组合的精密单点定位模型[8]为:
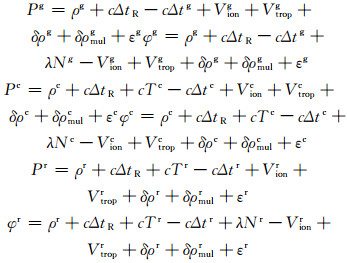
|
式中,上标g、r、c分别代表GPS、GLONASS、BDS,ρ表示卫星到接收机间的几何距离,P表示伪距观测值,φ表示载波相位观测值,ΔtR表示接收机钟差,Δtg、Δtr、Δtc分别表示3个系统的卫星钟差,λ表示观测值波长,N表示整周模糊度,Vion表示电离层延迟,Vtrop表示对流层延迟,δρ表示星历误差,δρmul表示多路径效应延迟,ε表示其他项改正。
采用德国地学中心(GFZ)提供的精密星历和精密钟差进行数据处理,可以认为卫星轨道误差和卫星钟误差均已被消除[9]。多系统组合的消电离层(LC)组合可以表示为:
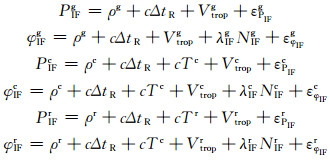
|
式中,PIF表示消电离层组合的伪距观测值,εPIF表示除去电离层延迟的其他误差,λIF表示消电离层组合对应的波长,NIF表示消电离层组合模糊度。
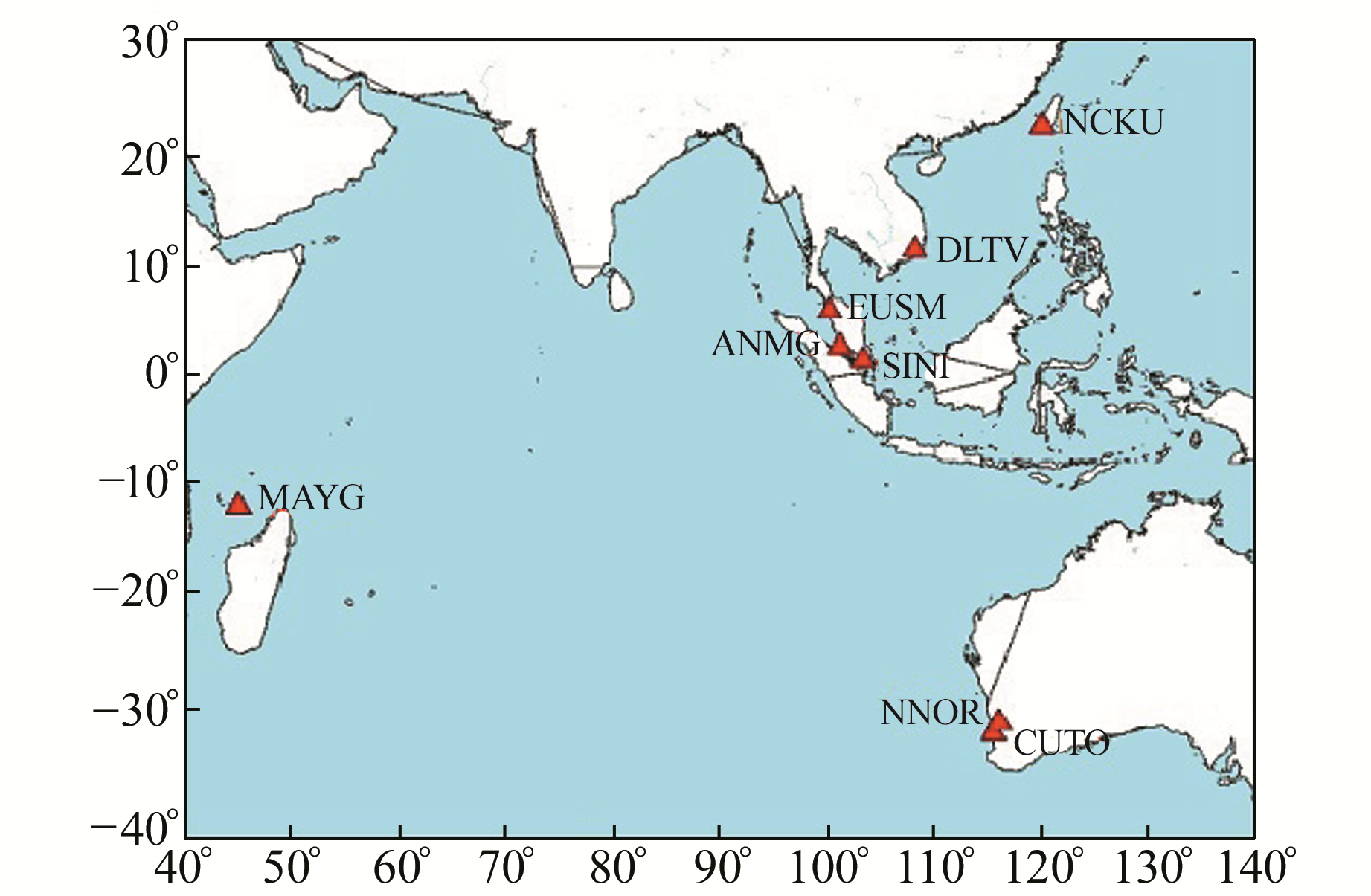
2 数据处理与分析 2.1 数据处理流程本实验采用可以采集到GPS、GLONASS、BDS等系统观测数据的MGEX站2016-02-19~02-28数据,测站分布如图 1所示。
|
图 1 MGEX测站分布 Fig. 1 Distribution of MGEX stations |
解算时,设置采样间隔为300 s,使用LC和PC的组合非差观测模型,观测值权重按照GPS:GLONASS:BDS=2:2:1的定权方式,采用IGS提供的天线信息改正GPS和GLONASS卫星的PCO和PCV,目前没有机构提供北斗卫星的PCV和PCO信息,只能对其进行概略改正。同时考虑了对流层(使用Saastamoinen模型[10]改正湿分量,干分量通过参数估计)、电离层(使用LC组合消除)、天线相位缠绕、固体潮、海洋潮、极移等改正,采用最小二乘方法进行参数估计[11],解算流程如图 2所示。
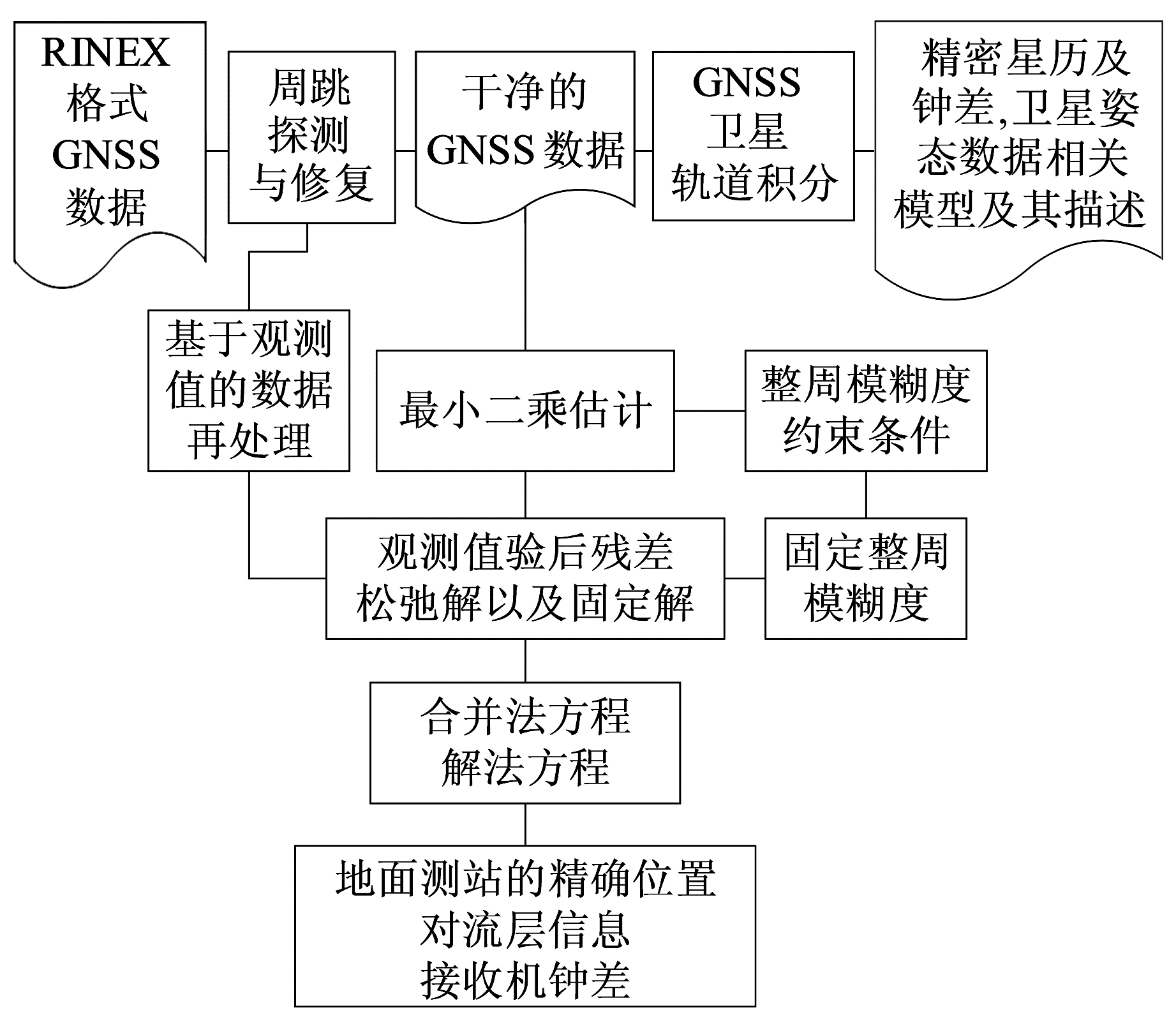
|
图 2 数据处理流程 Fig. 2 Data processing flow chart |
对观测站采用单个系统的G和C以及R、双系统组合的G/C和G/R以及R/C、三系统的G/R/C共7种系统组合,截止高度角采用5°~60°不等间距84种情况分别进行数据解算。为减小系统误差、防止出现粗差,本文将2016-02-19~02-28解算结果求均值,并剔除存在粗差的数据(RMS大于3倍的中误差)。
2.2 可见卫星数分析由于采用的是1 d的数据,观测时间较长,所有站点总有时间段能观测到足量的卫星进行定位,但在实际中并非如此,常存在一个时段内卫星可见数量不能达到所需的最少数量。本文按照单点定位原理[12]作出以下判定:若1 d内单系统组合平均每个历元可以观测到的卫星小于4颗(待估参数有3个测站坐标参数X、Y、Z、4个整周模糊度、对流层信息以及接收机钟差),双系统组合平均每个历元可以观测到的卫星小于5颗(待估参数有3个测站坐标参数X、Y、Z、5个整周模糊度、1个时间系统差异、对流层信息以及接收机钟差),三系统组合平均每个历元可以观测到的卫星小于6颗(待估参数有3个测站坐标参数X、Y、Z、6个整周模糊度、2个时间系统差异、对流层信息以及接收机钟差),则认为不能定位。各个站的平均可见卫星数如图 3所示。
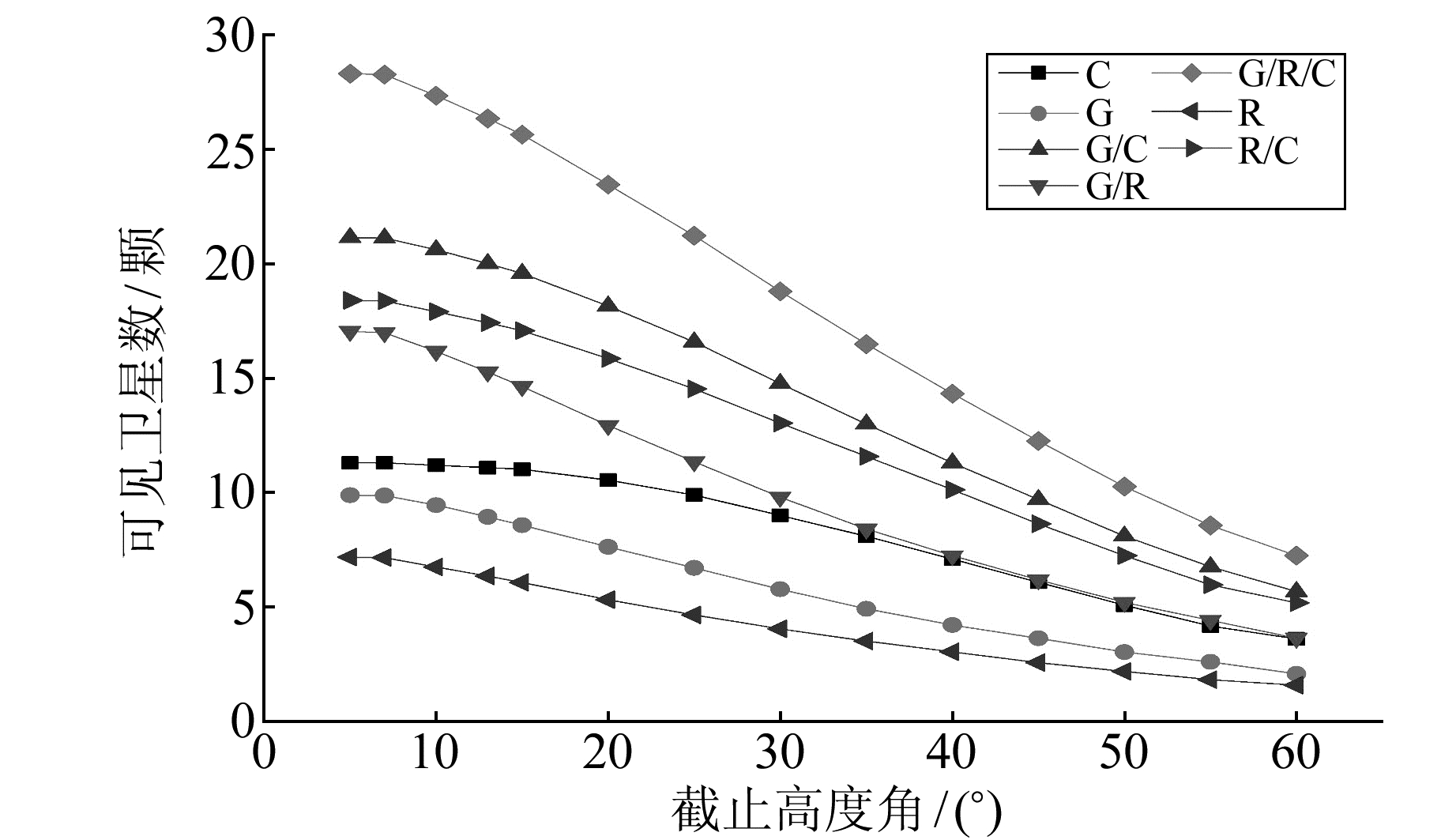
|
图 3 卫星数量随截止高度角变化 Fig. 3 The number of satellites varies with the height of masking angle |
各种系统组合进行GNSS PPP的最大截止高度角见表 1。
|
|
表 1 各个系统的最大截止高度角 Tab. 1 Maximum masking angle of each system |
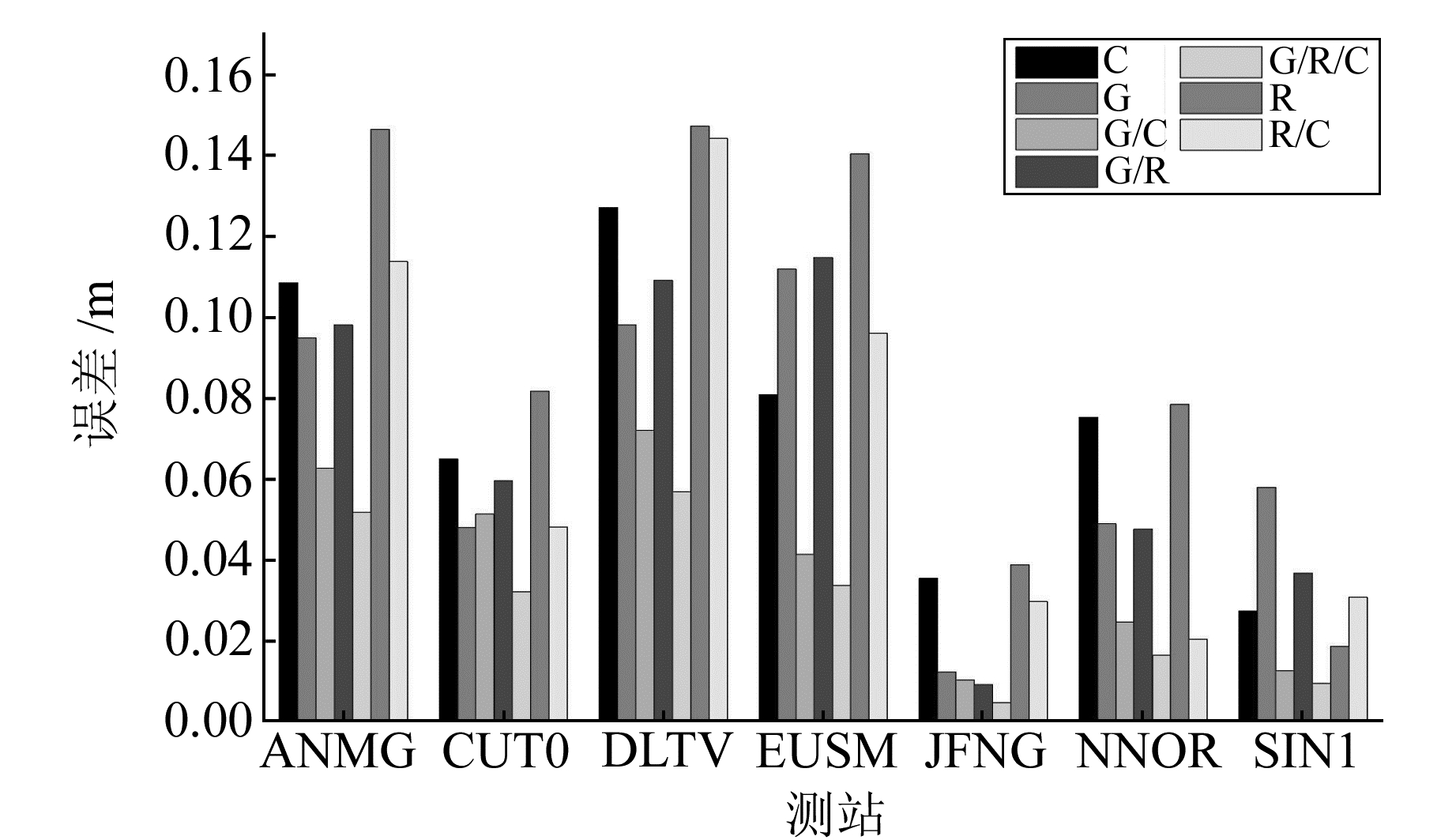
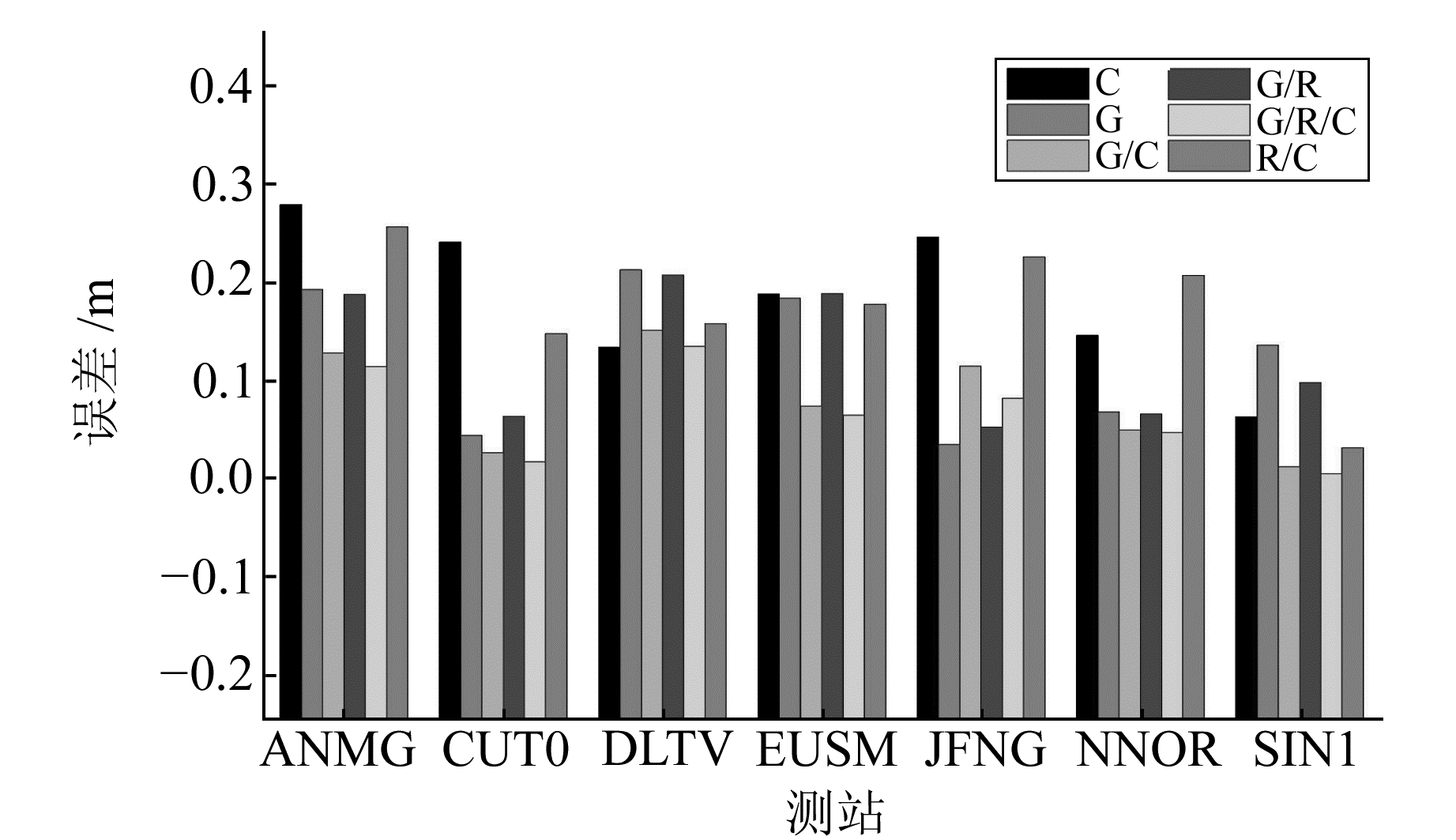
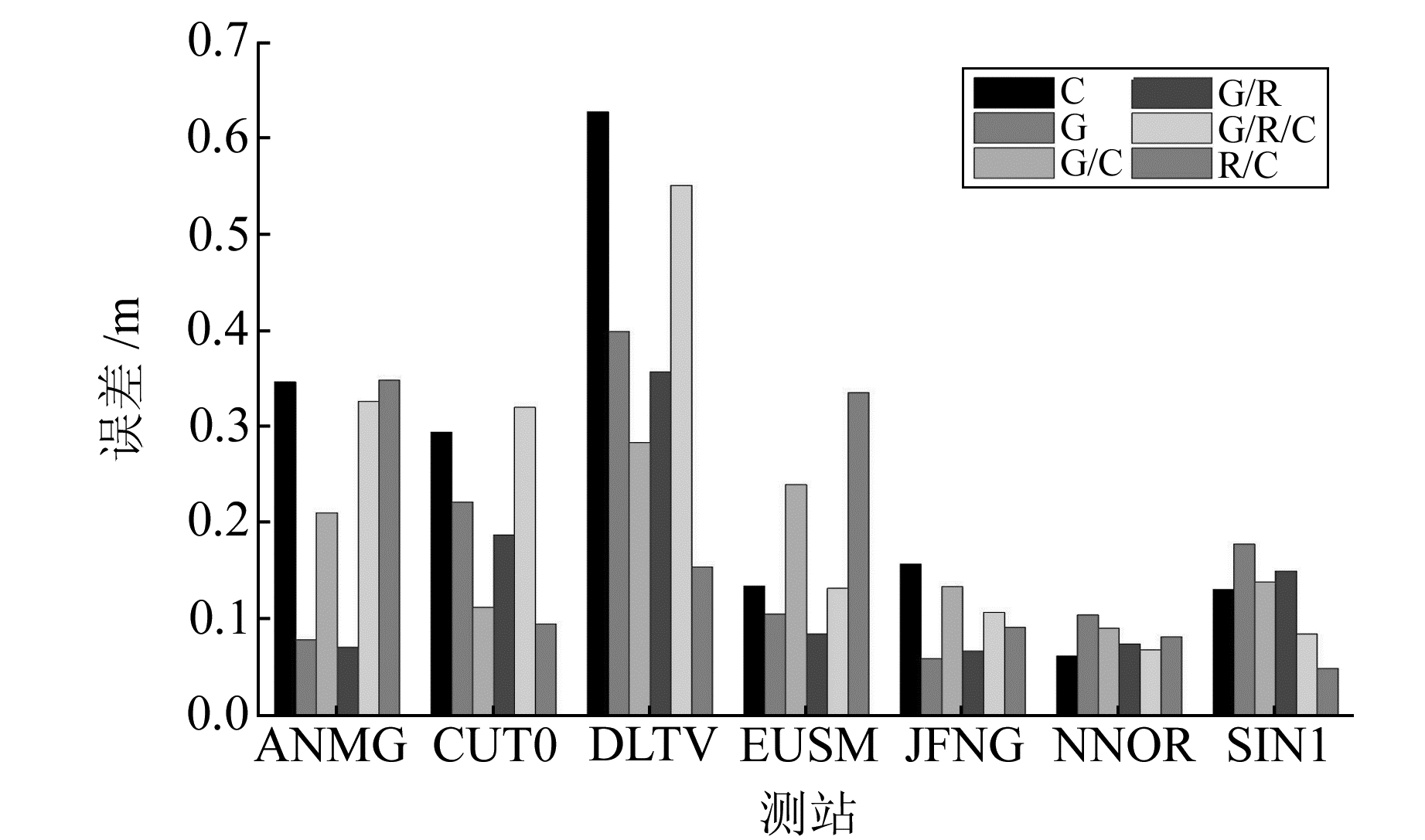
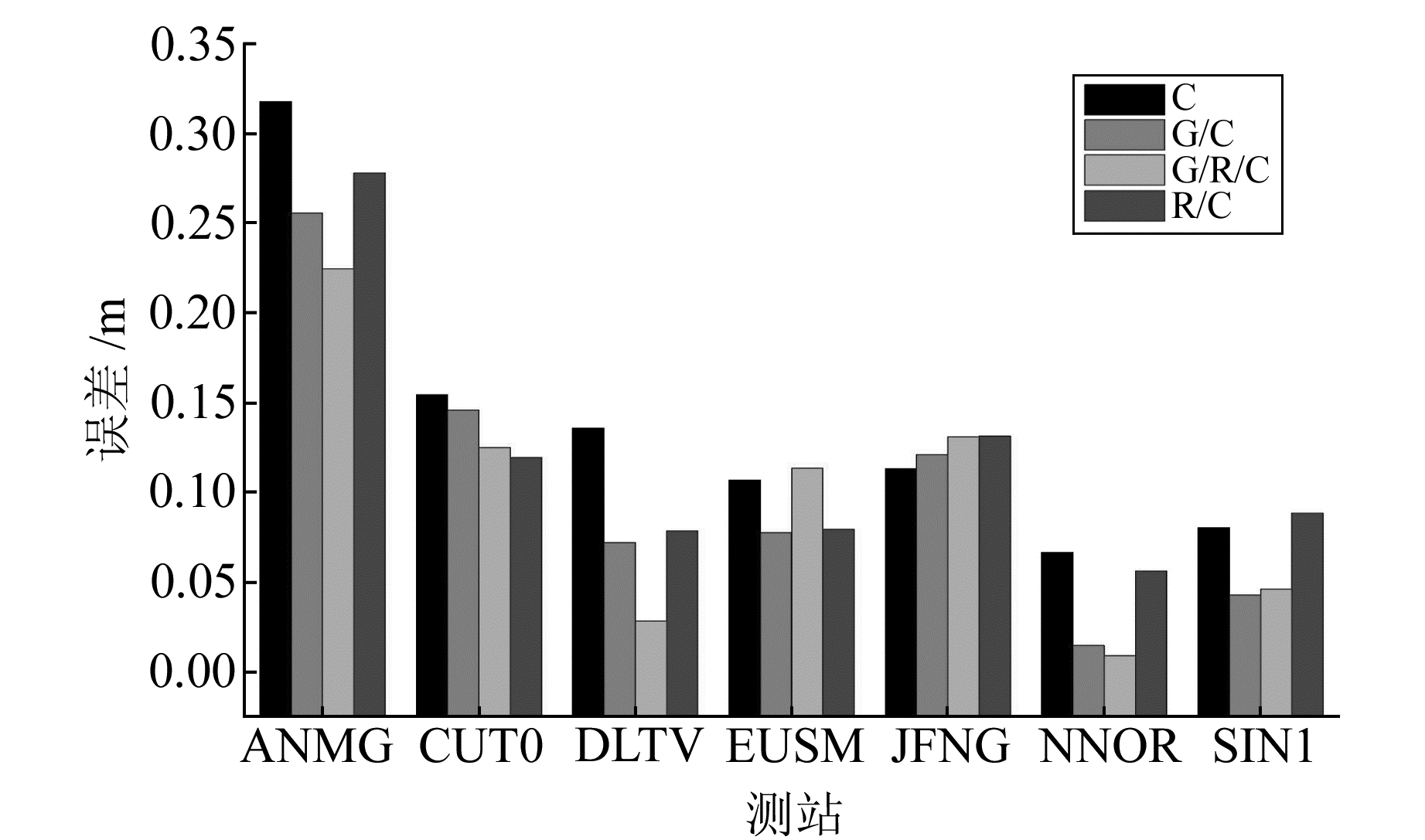
由于未找到官方公布的最新的MGEX站坐标,但PANDA软件的定位精度在mm级[11],所以选取PNDA软件截止高度角为10°、13°、15°的7种不同系统组合(G、C、R、G/C、G/R、R/C、G/R/C)一共21种情况的精密单点定位结果的均值作为真值(在解算时观测值已经赋权,所以这里认为最终得到的定位结果都是等精度的)。为减小误差,对所求的结果进行统计检查,当解算结果与均值差超过3倍均方根时,认为该情况下的解算结果存在粗差,应将该站舍弃。经过检验,所有的观测数据解算结果均没有超限。图 4~9给出了不同系统组合、不同截止高度角的精度对比结果(限于篇幅,文中仅给出部分图)。
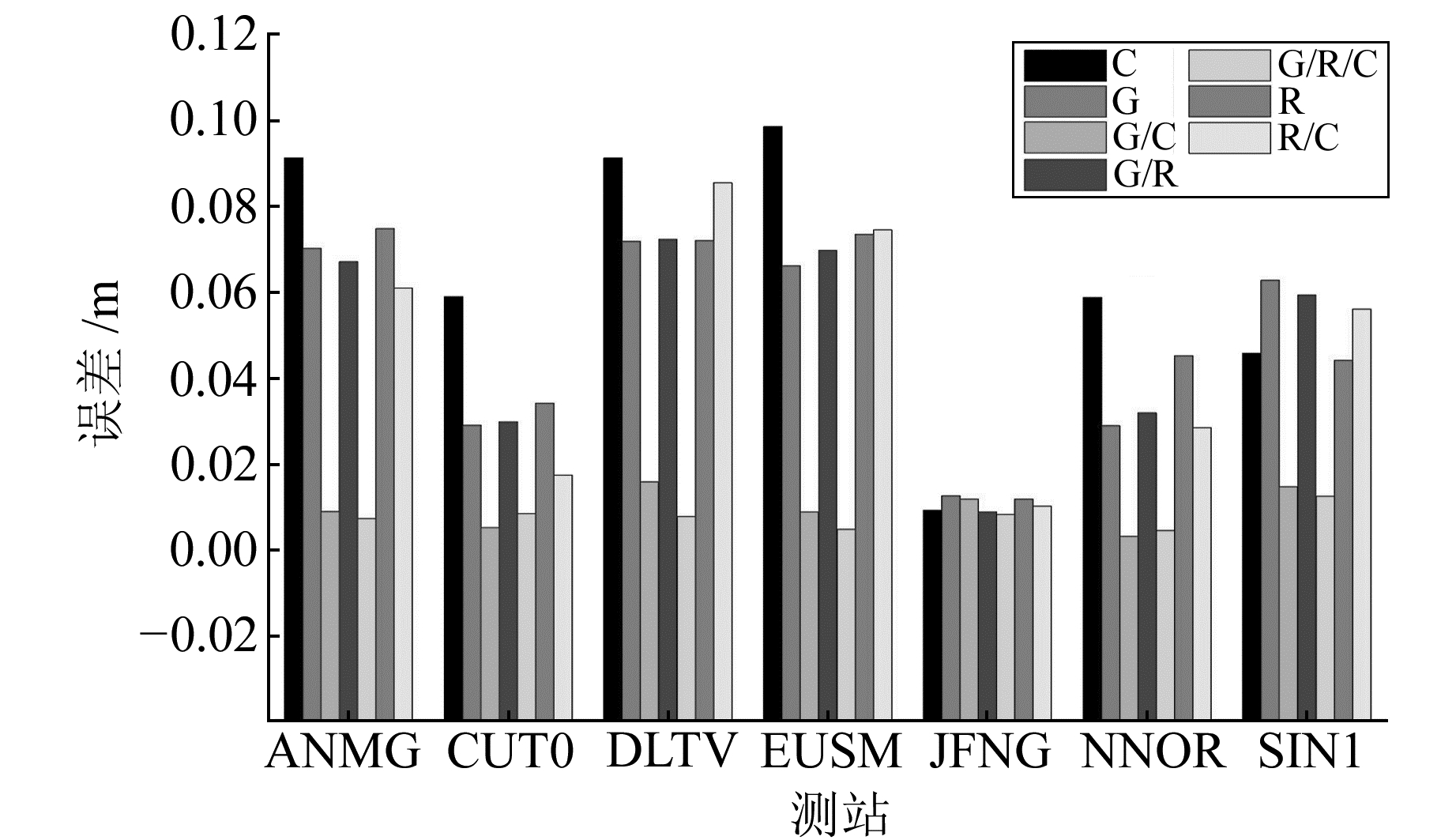
|
图 4 5°截止高度角下的精度 Fig. 4 The precision of 5° masking angle |
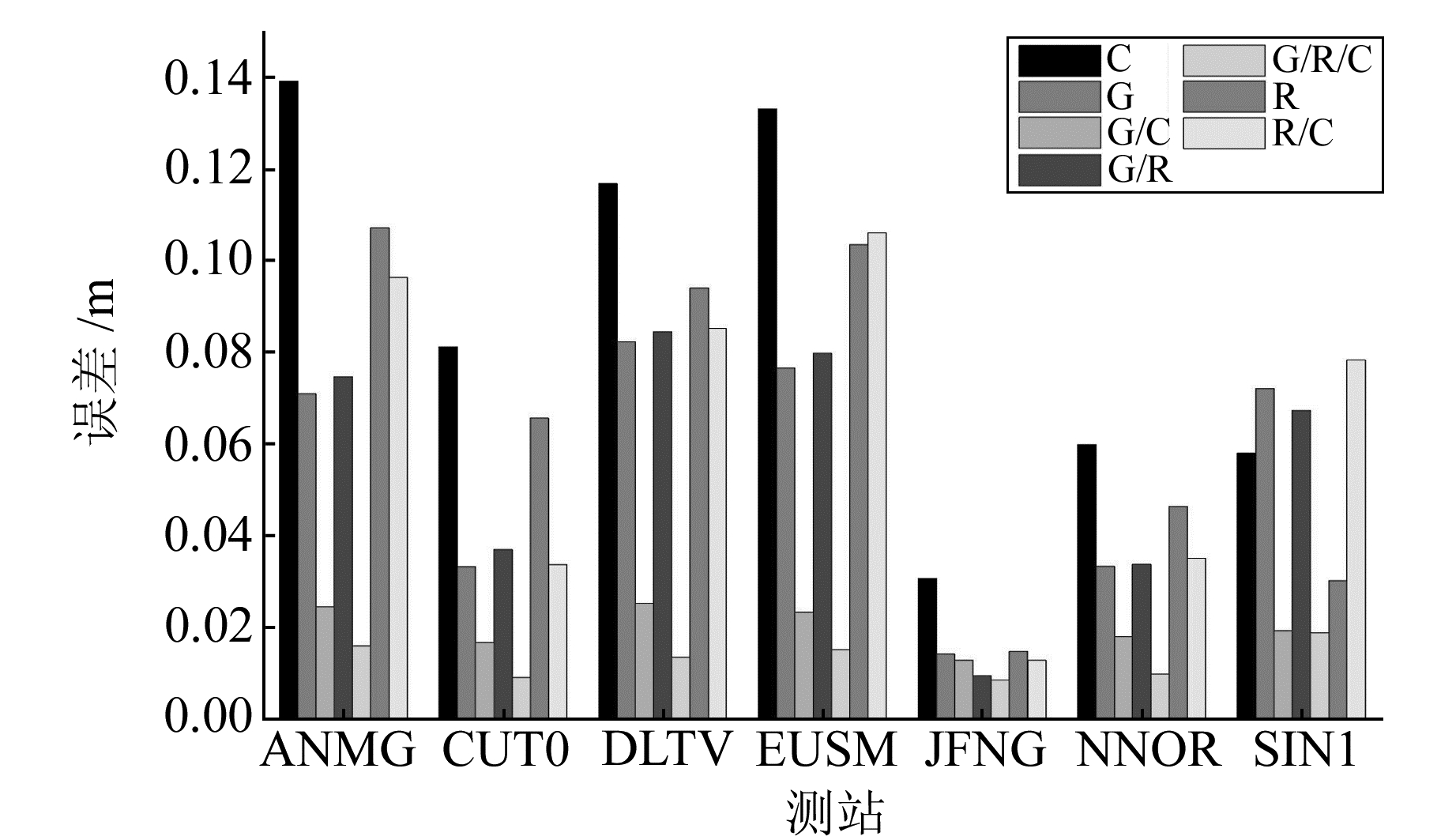
|
图 5 15°截止高度角下的精度 Fig. 5 The precision of 15° masking angle |
|
图 6 25°截止高度角下的精度 Fig. 6 The precision of 25° masking angle |
|
图 7 35°截止高度角下的精度 Fig. 7 The precision of 35° masking angle |
|
图 8 45°截止高度角下的精度 Fig. 8 The precision of 45° masking angle |
|
图 9 55°截止高度角下的精度 Fig. 9 The precision of 55° masking angle |
由图 4~9可以得出,当截止高度角较低(小于25°)时,G/R/C组合的精度最高,G/C次之,G、R、R/C和G/R精度相当,C最低;当截止高度角增加(25°~35°)时,C的精度有所提高,与G、R/C、G/R基本相当且与G/C、G/R/C的定位精度差距减小,R的定位精度极度下降,甚至不能定位;当截止高度角进一步增加(35°~45°)时,G、G/R的定位精度比较高、G/R/C次之,其余系统大体相同;当到达45°以上时,不借助BDS卫星无法定位,此时的定位精度基本相同。
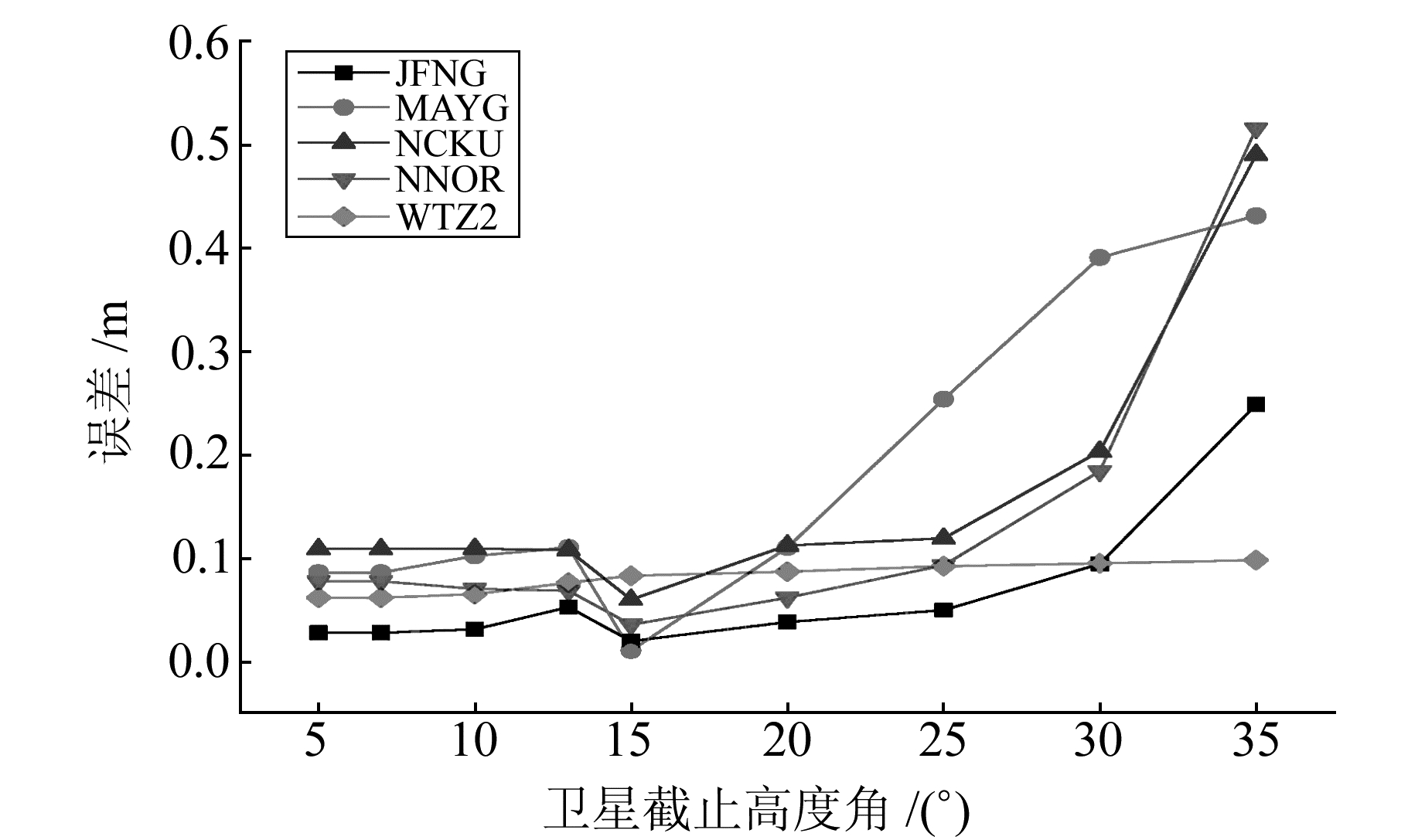
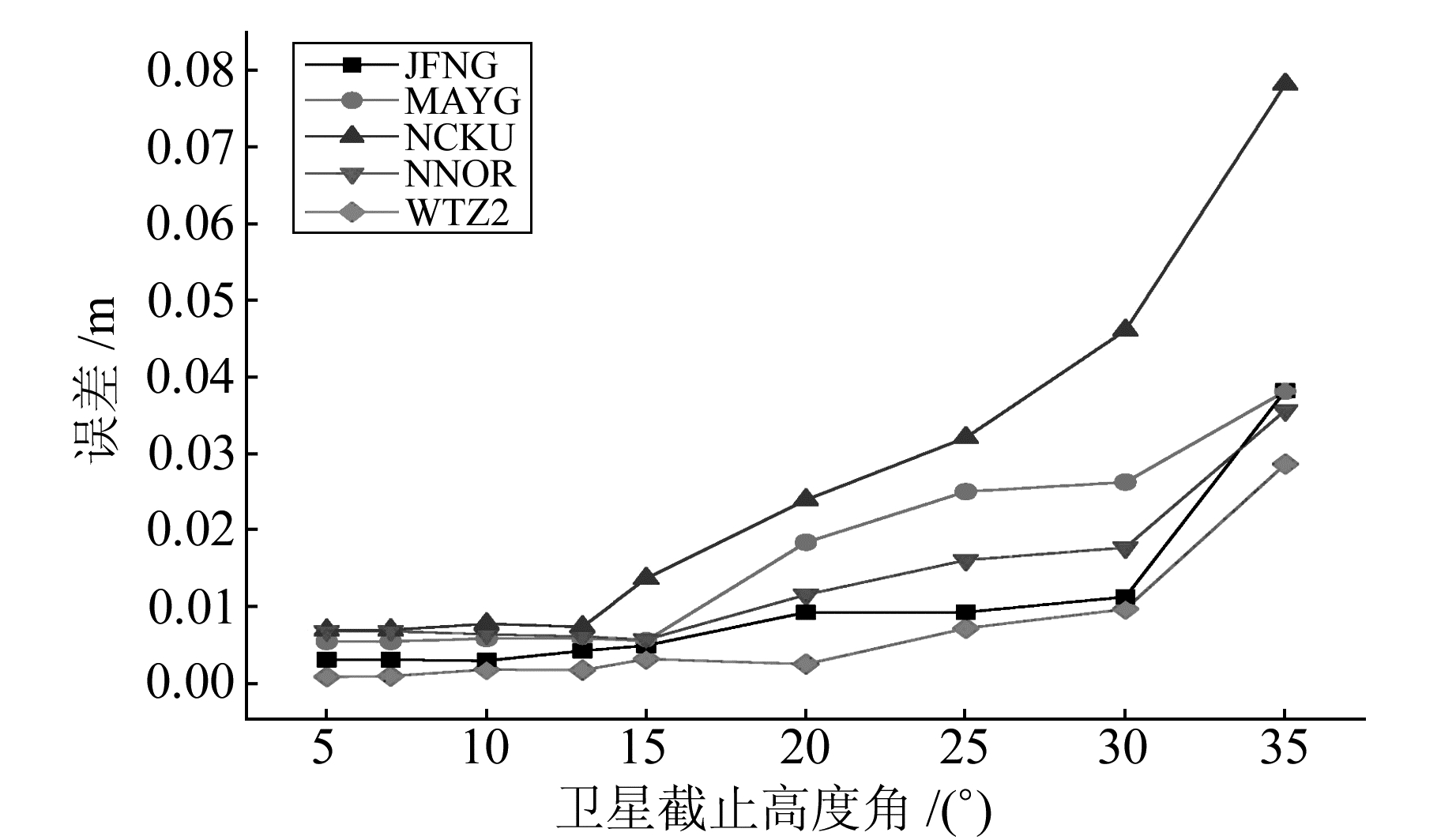
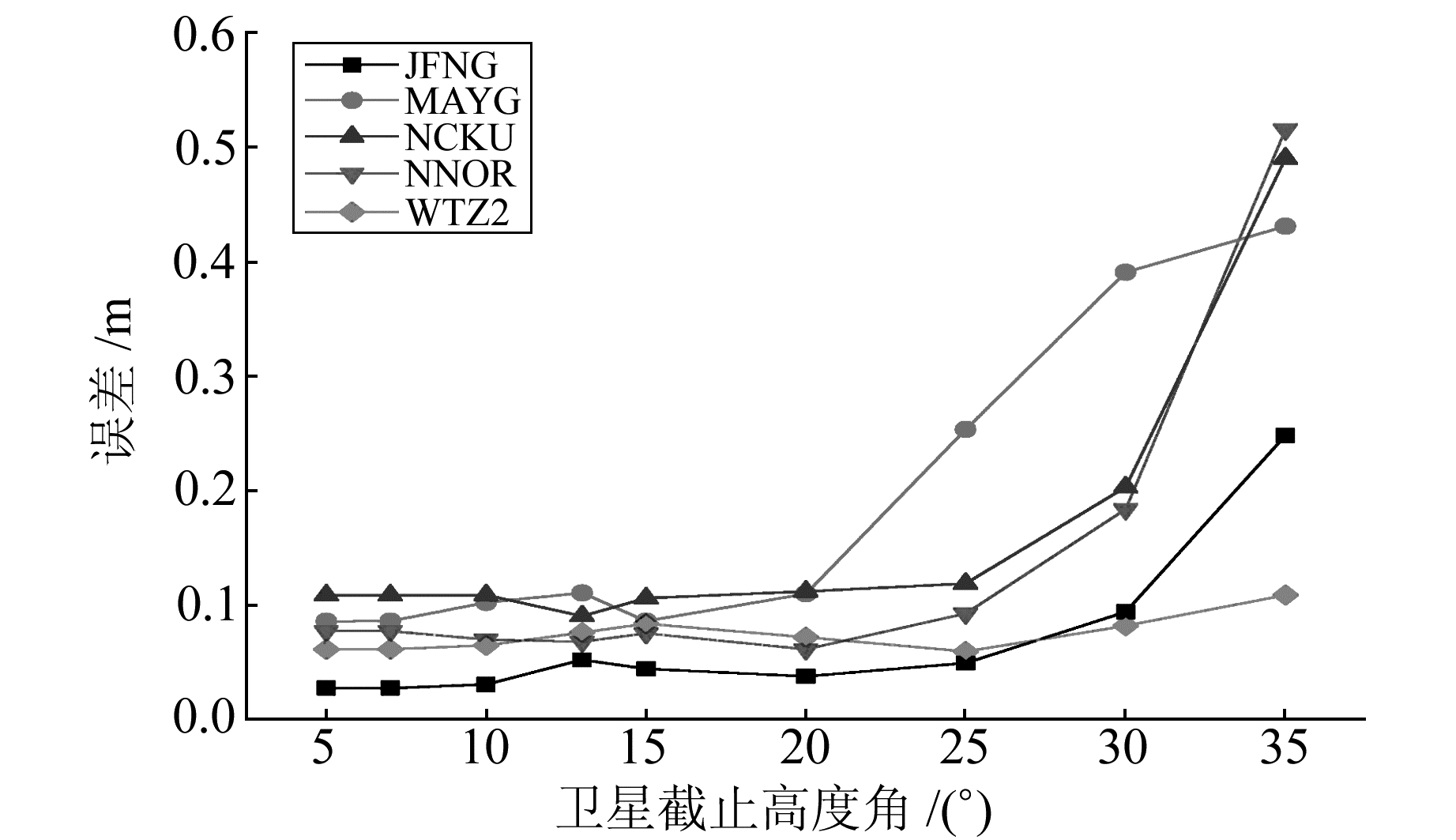
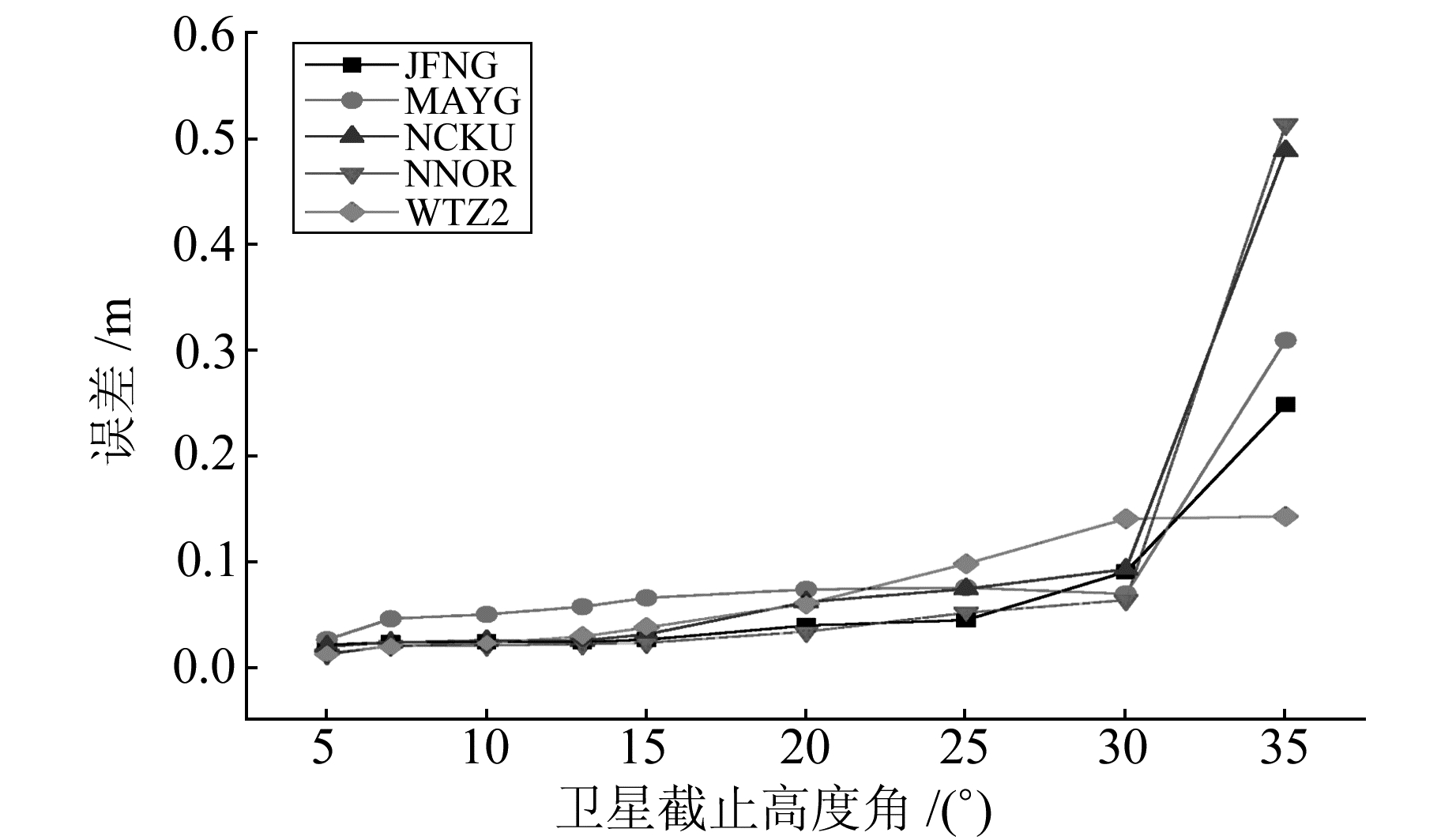
2.4 不同系统组合的最优截止高度角当卫星高度角较低时,因为信号遮挡等原因产生过多的周跳以及对流层湿延迟估计不准确而产生较大的误差。随着卫星高度角的增加,周围的遮挡物逐渐减少,对流层湿分量变化逐渐稳定,可通过模型进行修正。但此时的卫星可见数减少,可能会导致测量精度降低。为了探讨最合适的卫星截止高度角,本文选出5个MGEX(JFNG、MAYG、NCKU、NNOR、WTZ2)站,采用和以上同样的计算方式,最后得到的点位精度见图 10~16。
|
图 10 单C的精度 Fig. 10 Precision of only BDS |
|
图 11 单G的精度 Fig. 11 Precision of only GPS |
|
图 12 G/C组合的精度 Fig. 12 Precision of GPS/BDS combination |
|
图 13 G/R组合的精度 Fig. 13 Precision of GPS/GLONASS combination |
|
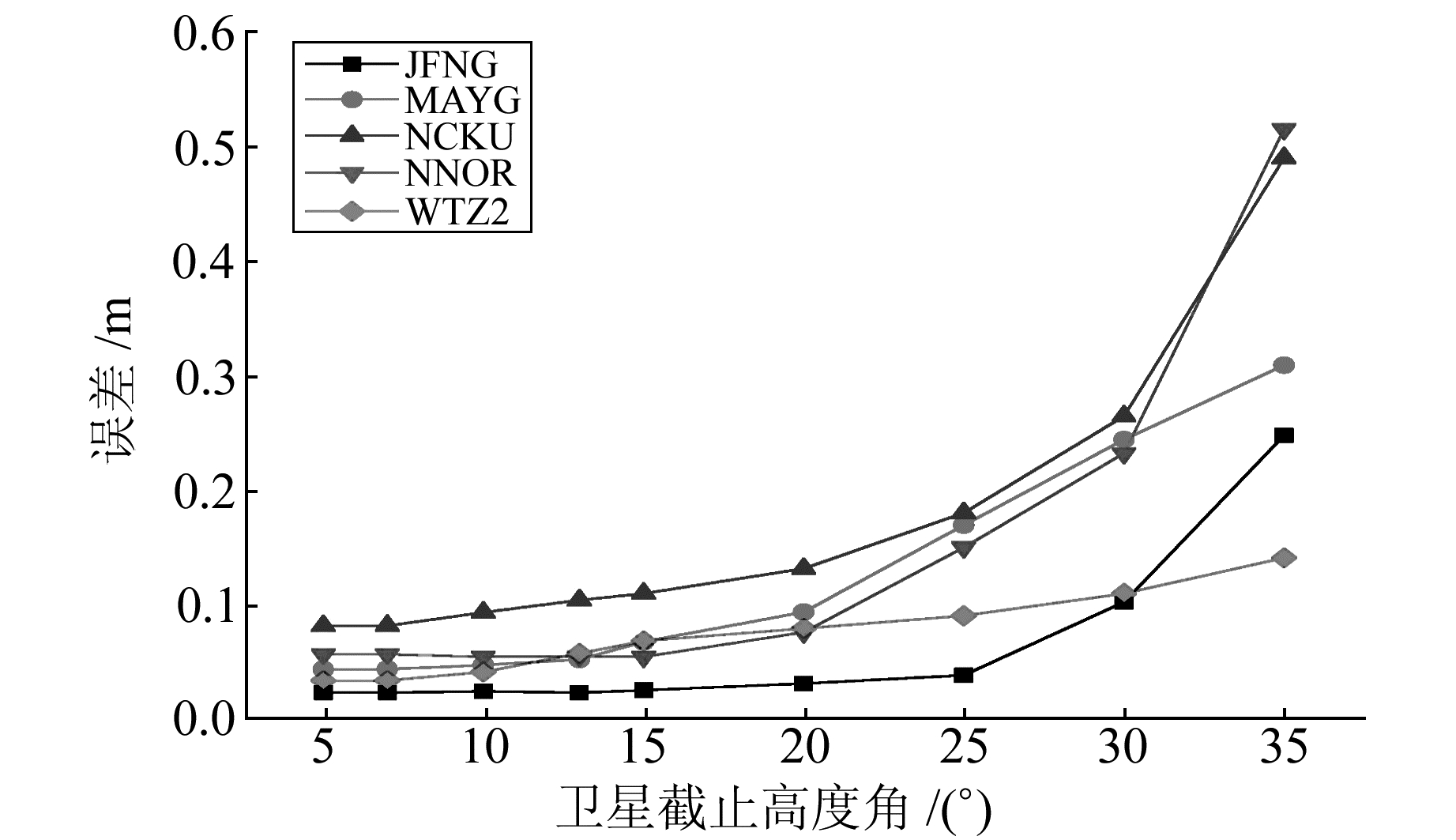
图 14 G/R/C组合的精度 Fig. 14 Precision of GPS/GLONASS/BDS combination |
|
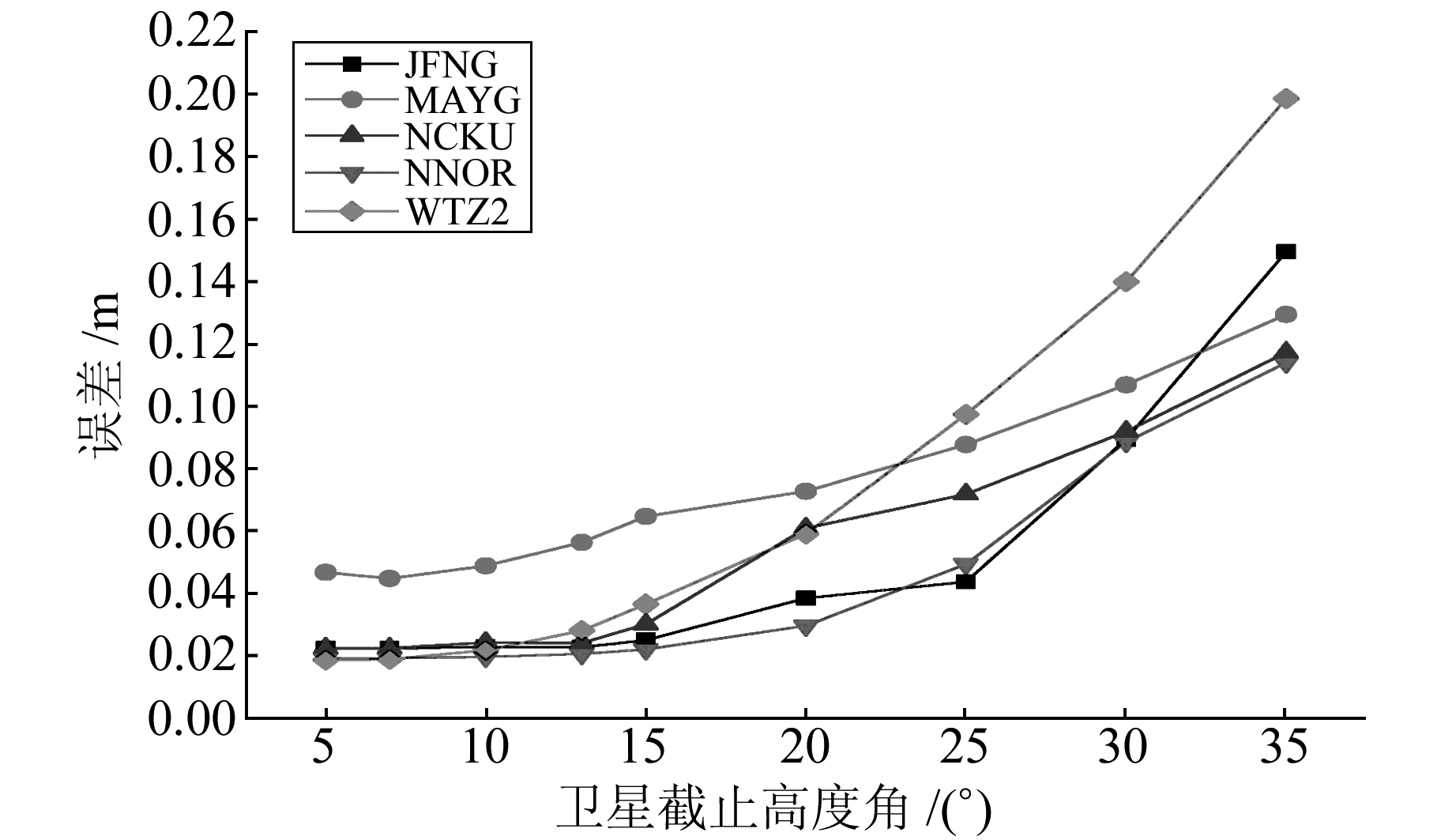
图 15 单R的精度 Fig. 15 Precision of only GLONASS |
|
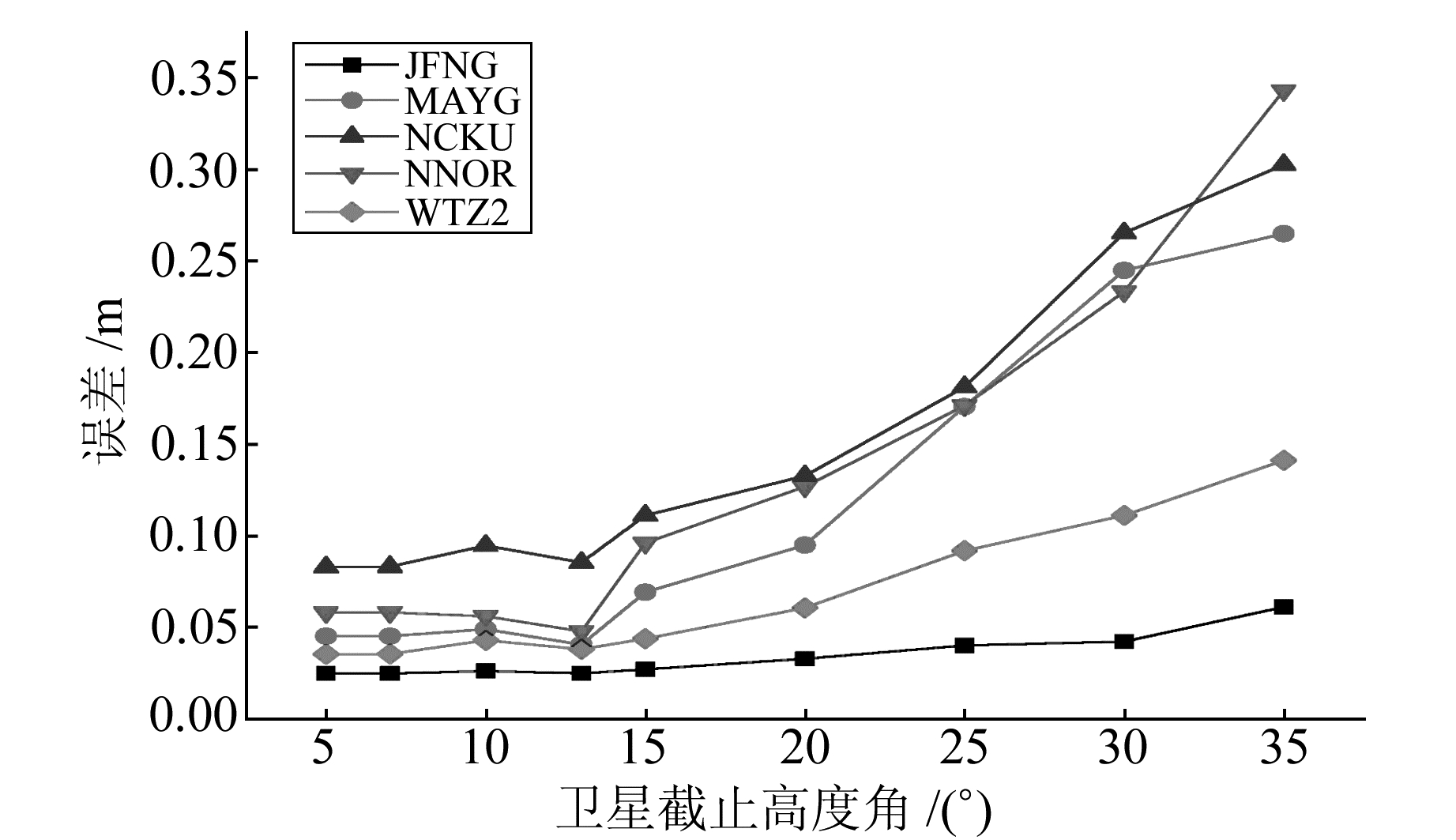
图 16 R/C组合的精度 Fig. 16 Precision of GLONASS/BDS combination |
由于最优的截止高度角一般在5°~25°,这里给出5°~35°截止高度角下各个系统组合的定位精度。由图可知,在采用单C系统进行定位时,最优的截止高度角为15°左右;采用单G时,最优的截止高度角为13°左右;采用G/C进行定位时,应在10°左右;采用G/R时,最优卫星截止高度角为7°;采用G/C/R进行定位时,最优的截止高度角为10°左右;采用R进行定位时,最优高度角为10°左右;采用G/C进行定位时,最优截止高度角为13°左右。
3 结语GNSS技术用于煤矿时,由于测量环境的特殊性,观测位置难以人为选定,最小截止高度角常取决于煤矿的边坡坡度。在允许的条件下建议将截止高度角设置在7°~15°,当条件不允许时可以依照具体情况将截止高度设置得尽可能小。使用单系统定位时,截止高度角应设置在30°以下,双系统应设置在40°以下,三系统应设置在55°以下,最优截止高度角均在10°~15°。当截止高度角小于25°时,定位精度最高的为G/C/R系统,最低的为单C系统;当截止高度角从25°上升至40°时,各个系统组合的定位精度逐渐接近;当截止高度角增大至40°以上时,所有可以定位的系统组合精度基本相同,此时定位主要依靠北斗卫星,北斗的优势逐渐体现出来。
| [1] |
Gu Q H, Lu C W, Li F B, et al. Mining Production Information Management System in an Open-Pit Based on GIS/GPS/GPRS/RFID[J]. Journal of Coal Science & Engineering, 2010, 16(2): 176-181
(  0) 0) |
| [2] |
Shan Z Y, Han H Z, Jiang K. Optimization Model of GNSS/Pseudofiles Structure Design for Open-pit Mine Positioning[J]. Transactions of Nonferrous Metals Society of China, 2013(7): 2 201-2 208
(  0) 0) |
| [3] |
丁赫, 孙付平, 李亚萍, 等. BDS/GPS/GLONASS组合精密单点定位模型及性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 303-307 (Ding He, Sun Fuping, Li Yaping, et al. Modeling and Performance Analysis of Combined BDS/GPS/GLONASS[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 303-307)
(  0) 0) |
| [4] |
刘经南, 叶世榕. GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报:信息科学版, 2002, 27(3): 234-240 (Liu Jingnan, Ye Shirong. GPS Precise Point Positioning Using Undifferenced Phase Observation[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 234-240)
(  0) 0) |
| [5] |
任超, 彭家頔, 佘娣, 等. 低高度角卫星信号对提高对流层估计精度的影响分析[J]. 大地测量与地球动力学, 2011, 31(6): 124-127 (Ren Chao, Peng Jiadi, She Di, et al. Effects of Low GPS Satellite Elevation Mask Angle on Estimation of Tropospheric Delay[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 124-127)
(  0) 0) |
| [6] |
Tegedor J, Melgard T, Vigen E, et al.Multi-GNSS Precise Point Positioning Including GPS, GLONASS, Galileo and Beidou[C].PPP: Reaching Full Potential, 2013
(  0) 0) |
| [7] |
李鹤峰, 党亚民, 秘金钟, 等. BDS与GPS、GLONASS多模组合导航定位时空统一[J]. 大地测量与地球动力学, 2013, 33(4): 73-78 (Li Hefeng, Dang Yamin, Bei Jinzhong, et al. Research on Spatio Tempora Unification of BDS/GPS/GLONASS Multi-mode Fusion Navigation and Positioning[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 73-78)
(  0) 0) |
| [8] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 (Li Zhenghang, Huang Jinsong. GPS Surveying and Date Processing[M]. Wuhan: Wuhan University Press, 2005)
(  0) 0) |
| [9] |
Cai C S, Luo X M, Zhu J J. Modified Algorithm of Combined GPS/GLONASS Precise Point Positioning for Applications in Open-Pit Mines[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(5): 1 547-1 553 DOI:10.1016/S1003-6326(14)63224-6
(  0) 0) |
| [10] |
Combrink A Z A, Combrinck W L, Moraal H. Near Real-Time Detection of Atmospheric Water Vapor Using the SADC GPS Network[J]. South African Journal of Science, 2004, 100: 436-442
(  0) 0) |
| [11] |
赵齐乐, 刘经南, 葛茂荣, 等. 用PANDA对GPS和CHAMP卫星精密定轨[J]. 大地测量与地球动力学, 2005, 25(2): 113-116 (Zhao Qile, Liu Jingnan, Ge Maorong, et al. Precise Orbit Determination of GPS and CHAMP Satellites with PANDA Software[J]. Journal of Geodesy and Geodynamics, 2005, 25(2): 113-116)
(  0) 0) |
| [12] |
Li X, Ge M, Dai X, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
2. Jiangsu Key Laboratory of Resources and Environmental Information Engineering, China University of Mining and Technology, 1 Daxue Road, Xuzhou 221116, China
 2017, Vol. 37
2017, Vol. 37


