跨断层形变监测量不仅包含断层两盘相对构造运动信息,也包括气象、地下水位等因素造成的非构造活动信息[1],可通过多道维纳滤波、多元线性回归等方法[2-3]排除干扰因素影响,提取地震前兆信息。游丽兰等[4]考虑跨断层场地布设,建立了利用卡尔曼滤波处理跨断层数据的函数模型和随机模型。但卡尔曼滤波是以最小均方误差为估计准则的递推估计算法,在非线性或非高斯情况下其性能急剧下降[5]。粒子滤波是基于贝叶斯采样估计的一种近似数值方法,不受模型状态量和误差高斯分布假设的约束,适用于任意非线性非高斯动态系统[6]。为解决粒子退化问题,Gordon等[7]引入重采样方法,Douc等[8]给出残差重采样算法的优越性。
本文基于跨断层单测线函数模型,采用残差重采样粒子滤波算法,对全国13个台站的水准(基线)观测数据与降水量、温度等辅助观测数据进行处理,并与卡尔曼滤波结果进行比较。
1 跨断层单测线动态系统模型跨断层单测线动态系统模型为:
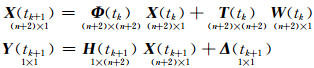
|
(1) |
式中,Φ(tk)=
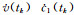
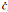

贝叶斯估计是在系统初始状态、噪声特征和测量信息已知的条件下,递推获得k时刻的状态向量:

|
(2) |
式中,xk和yk分别为k时刻的状态变量和观测变量,p(xk-1|y1:k-1)为k-1时刻状态变量的后验概率分布,p(xk|xk-1)为状态转移概率,p(xk|y1:k-1)为k时刻预测的状态变量先验概率分布,p(yk|xk)为根据新观测数据得到的似然函数。但式(2)的闭环解通常无法获得,因此应用受到限制。
2.2 残差重采样粒子滤波算法依据大数定理,采用蒙特卡洛方法求解贝叶斯估计中的积分运算,通过寻找一组在状态空间传播的加权粒子来近似状态变量的后验概率分布,当粒子数量N→∞时,可以逼近任何形式的概率密度分布。
记
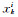

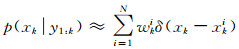
|
(3) |
式中,δ为Dirac函数,由于后验概率分布p(xk|y1:k)通常未知,因此采用重要性分布函数q(xk|y1:k)进行抽样,通常采用先验概率分布函数作为重要性分布函数,权值为:
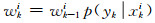
|
(4) |
状态变量估计值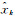
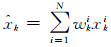
|
(5) |
本文采用残差重采样算法解决粒子退化问题,具体方法参考文献[9]。
3 数据处理采用粒子滤波进行数据处理,主要步骤如下。
1) 初始时刻k=0,根据已知先验概率分布p(x0)采样获得等权粒子集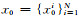
2) 读取跨断层观测数据,实现状态向量递推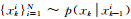
3) 计算似然函数
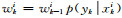
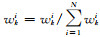
4) 根据粒子退化判断,若Neff < Nth(Neff=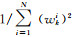


5) 计算状态向量估值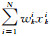
6) 判断循环是否结束,若是,则退出;否则令k=k+1,接收下一时刻测量值并执行步骤2)。
4 实例分析以大同台水准3-1、唐山台基线Ⅰ-Ⅱ和唐山台水准3-2等3条不同变化形态的测线为例,根据场地观测精度确定滤波参数,将残差重采样粒子滤波用于跨断层数据处理。
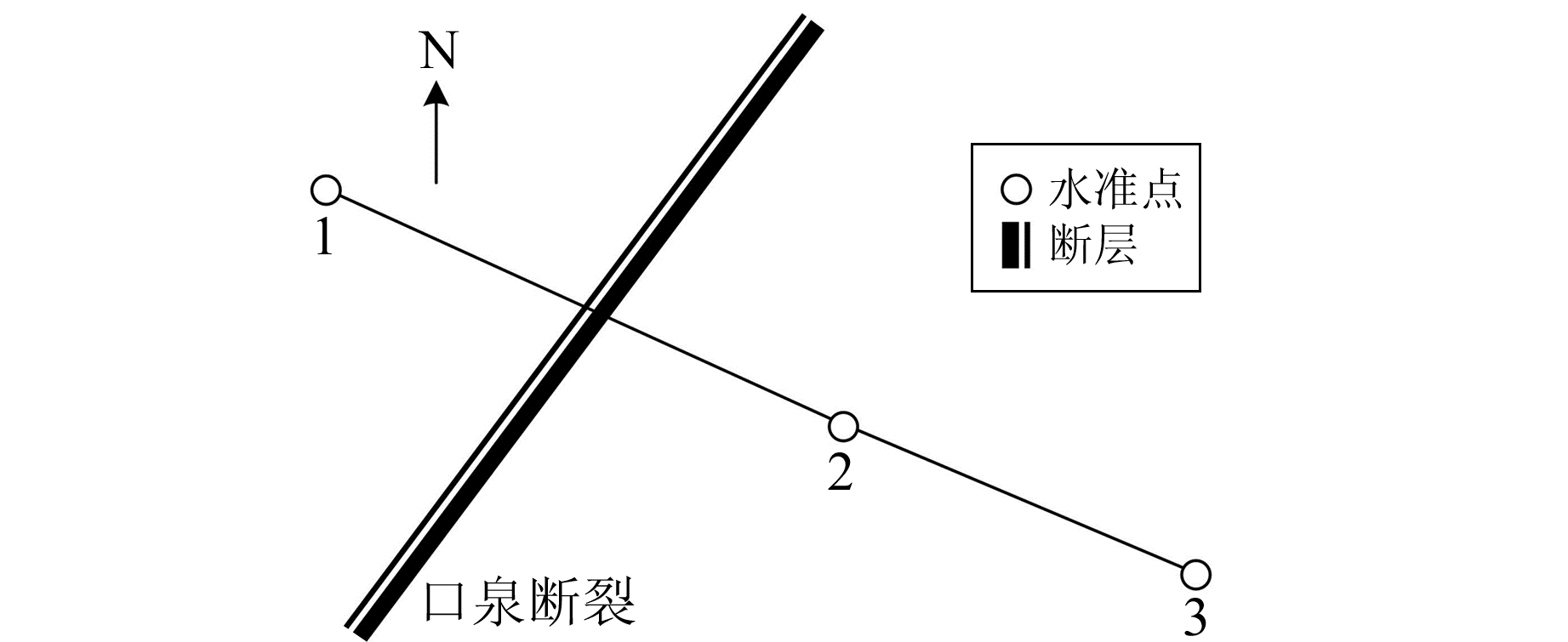
4.1 大同台水准测线3-1(图 1)跨口泉断裂,长约564 m,1点(基岩点)位于下盘,3点(土层点)位于上盘,每天进行跨断层短水准观测和辅助观测(气温、气压、地温和降水量)。
|
图 1 大同台水准测线布设 Fig. 1 Layout of Datong station |
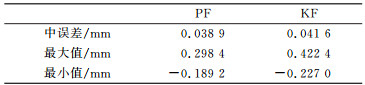
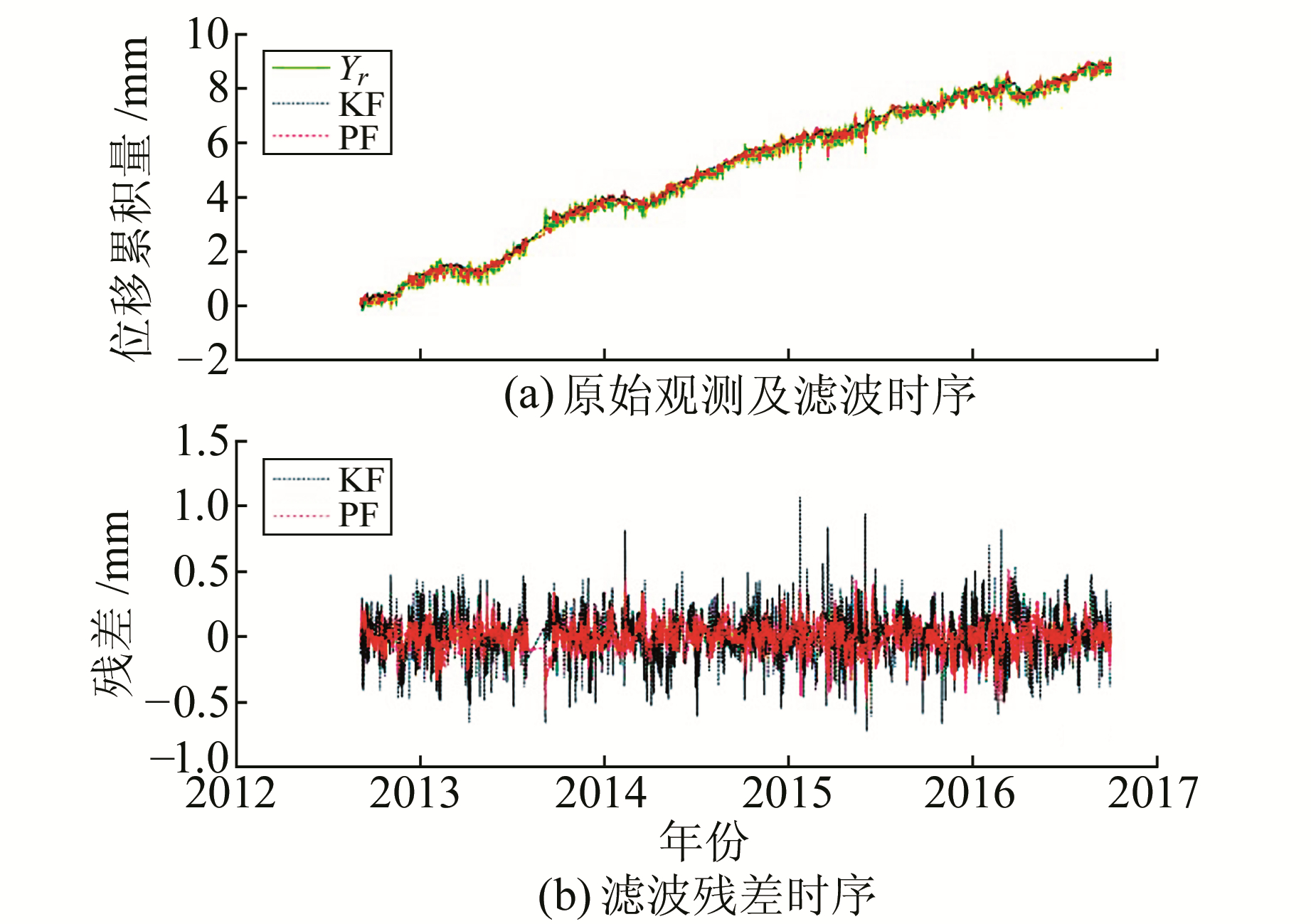
对2012-09~2016-09的水准观测数据分别进行残差重采样粒子滤波(PF)和卡尔曼滤波(KF)处理,结果见图 2和表 1。由图 2(a)看出,原始观测(Yr)、PF和KF时序均表明大同水准3-1变化趋势呈线性,图 2(b)和表 1说明PF比KF精度高。
|
图 2 大同水准3-1滤波值及残差值时序 Fig. 2 Filter value and residual sequence of Datong leveling line 3-1 |
|
|
表 1 大同水准3-1滤波残差统计 Tab. 1 Filter residuals of Datong leveling line 3-1 |
假设形变仅受辅助观测项影响,根据残差重采样粒子滤波计算环境因子(气温、降水量、气压、地温)对跨断层形变观测和断层运动的贡献,结果见图 3和图 4。

|
图 3 大同水准3-1环境因子及其形变影响 Fig. 3 Environmental observations and their influence on deformation of Datong leveling line 3-1 |
|
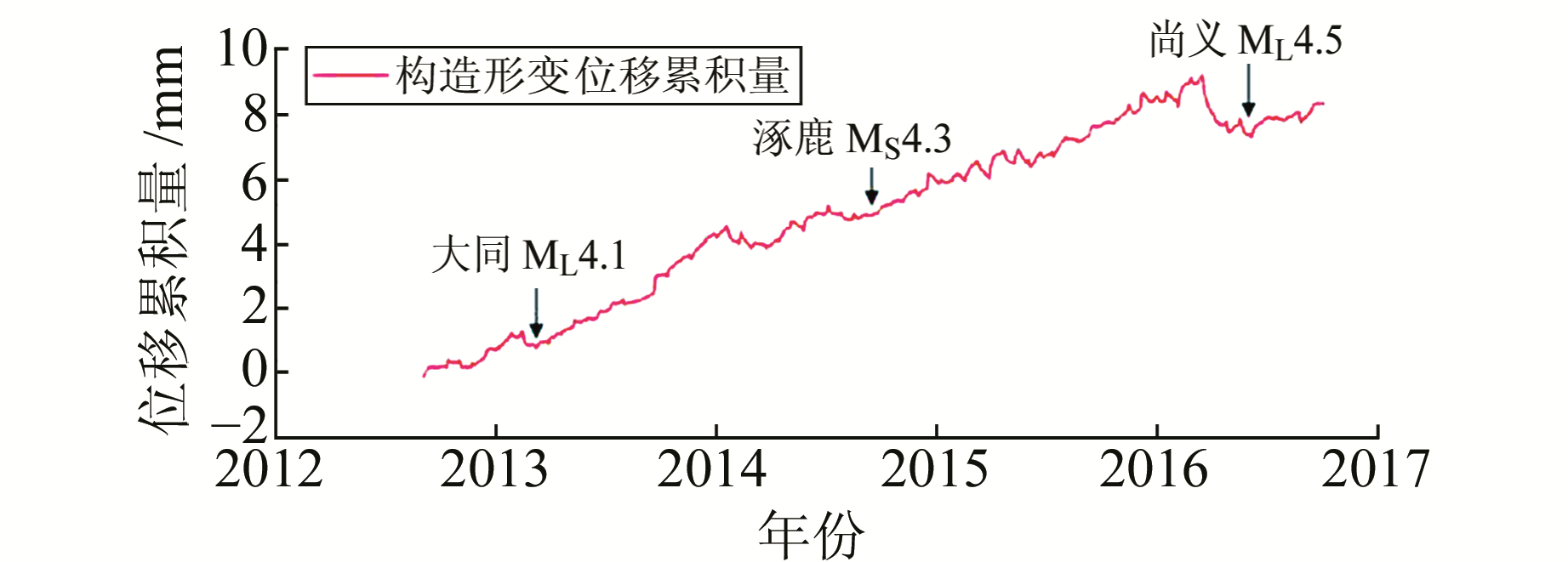
图 4 大同水准3-1构造形变位移累积量 Fig. 4 Tectonic deformation displacement cumulant of Datong leveling line 3-1 |
由图 3看出,气温对水准形变观测量的影响最大,约0.10 mm,与王秀文[10]给出的结论一致;降水量影响次之,小于0.10 mm;气压影响较小,小于0.05 mm;地温影响最小,约-0.01~0.01 mm。图 4表明,构造形变变化呈线性,2013-02-22山西大同ML4.1地震、2014-09-06河北涿鹿MS4.3地震和2016-06-23河北尚义ML4.5地震(震中距分别为56.7 km、184.5 km、121.3 km)前均出现明显的小幅破趋势转折下降变化。
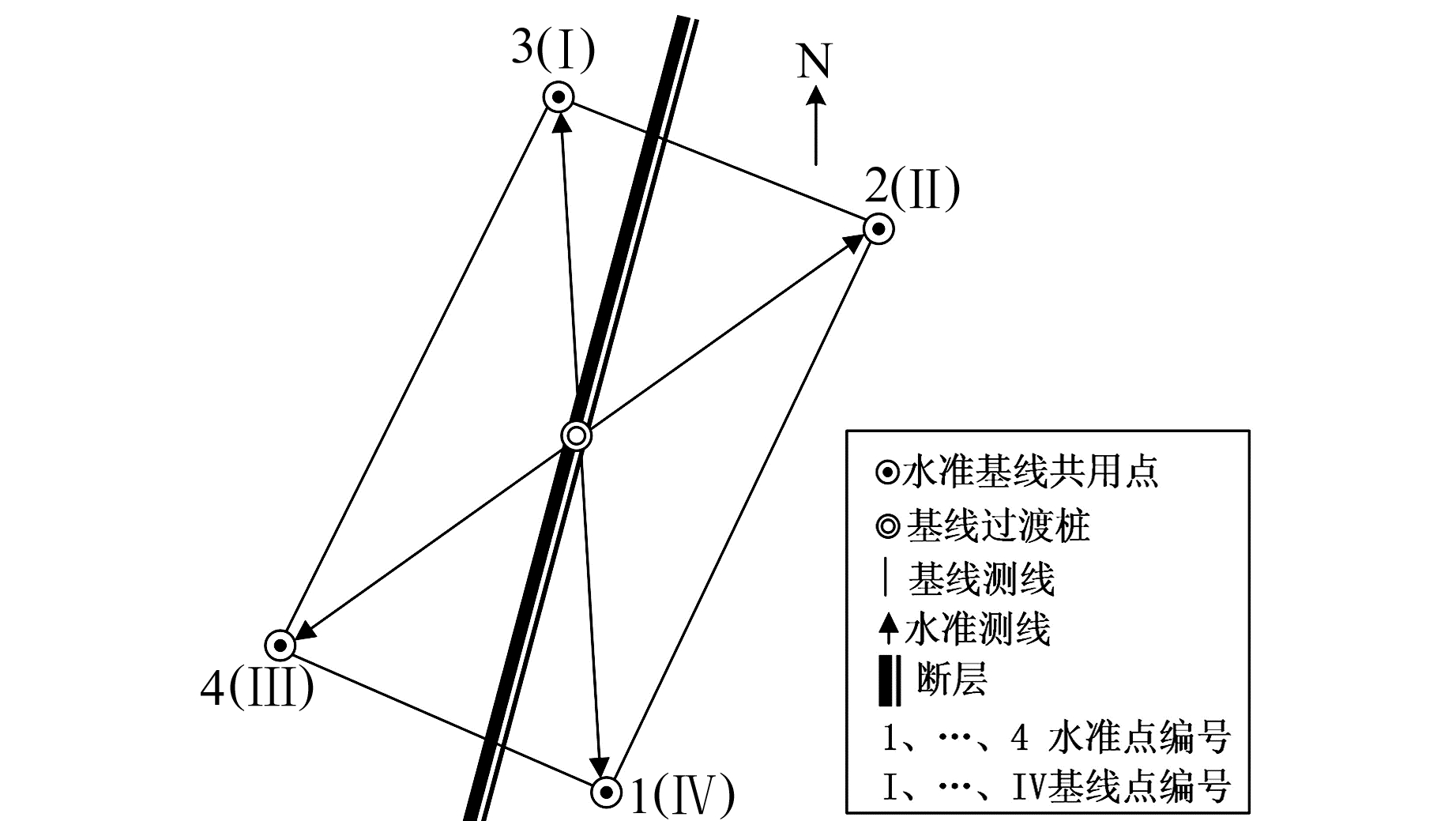
4.2 唐山台水准测线3-2、基线测线Ⅰ-Ⅱ(图 5)长约24 m,每天进行跨断层短水准、短基线观测和辅助观测(气温、降水量)。
|
图 5 唐山台测线布设 Fig. 5 Layout of Tangshan station |
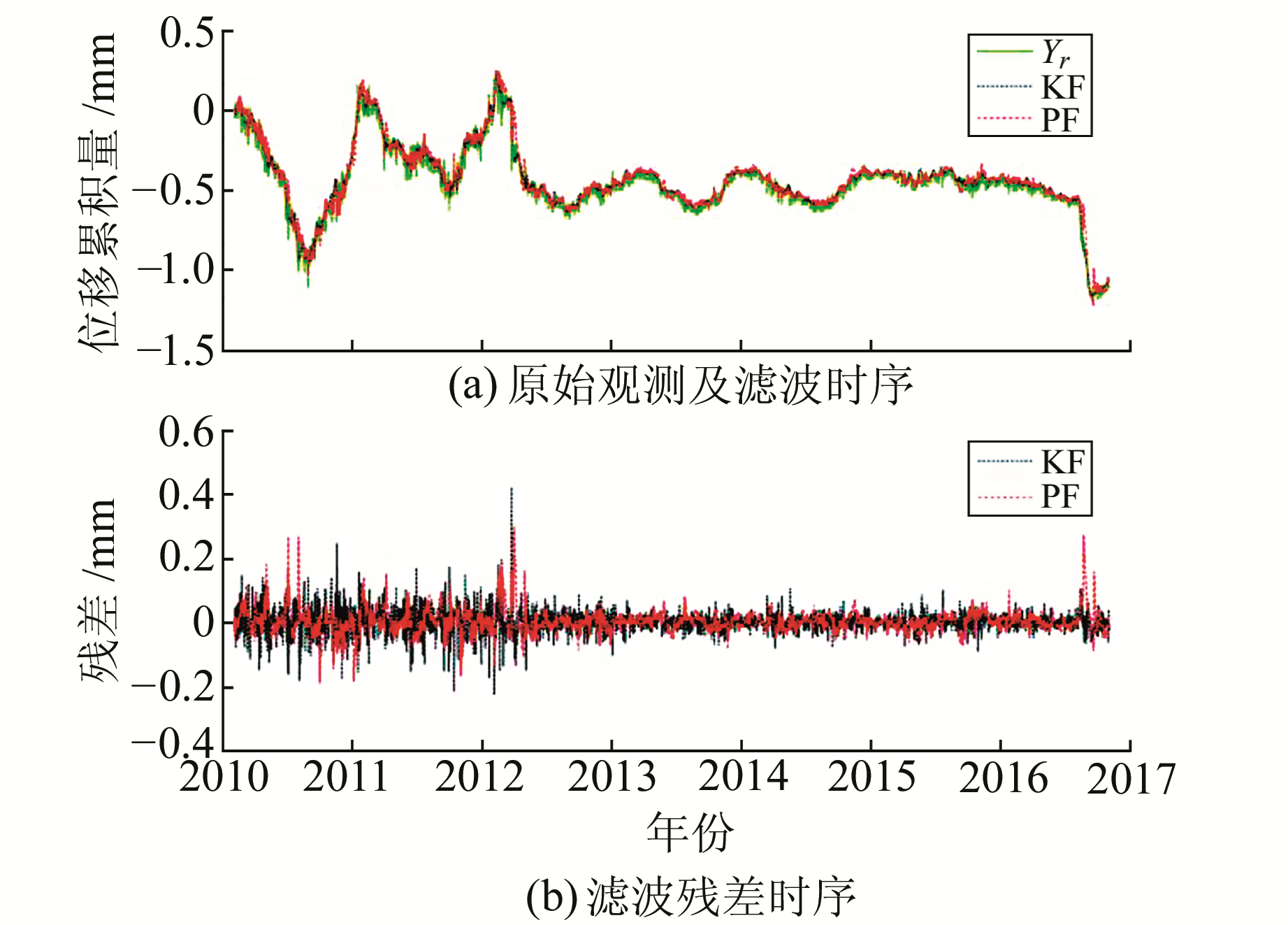
1) 基线Ⅰ-Ⅱ。对2010-02~2016-10的基线观测数据分别进行PF和KF处理,并对结果进行统计(图 6、表 2)。由图 6(a)可知,唐山基线Ⅰ-Ⅱ近7 a来形态多变:2012年之前呈波动状态并具一定的年周期性,2012-06~2015-01年变幅度明显减小,2015年后年变消失,2016-07后大幅下降后有所回升。图 6(b)和表 2表明,PF的精度略优于KF。
|
图 6 唐山基线Ⅰ-Ⅱ滤波值及残差值时序 Fig. 6 Filter value and residual sequence diagram of Tangshan baseline Ⅰ-Ⅱ |
|
|
表 2 唐山基线Ⅰ-Ⅱ滤波残差统计 Tab. 2 Filter residuals of Tangshan baseline Ⅰ-Ⅱ |
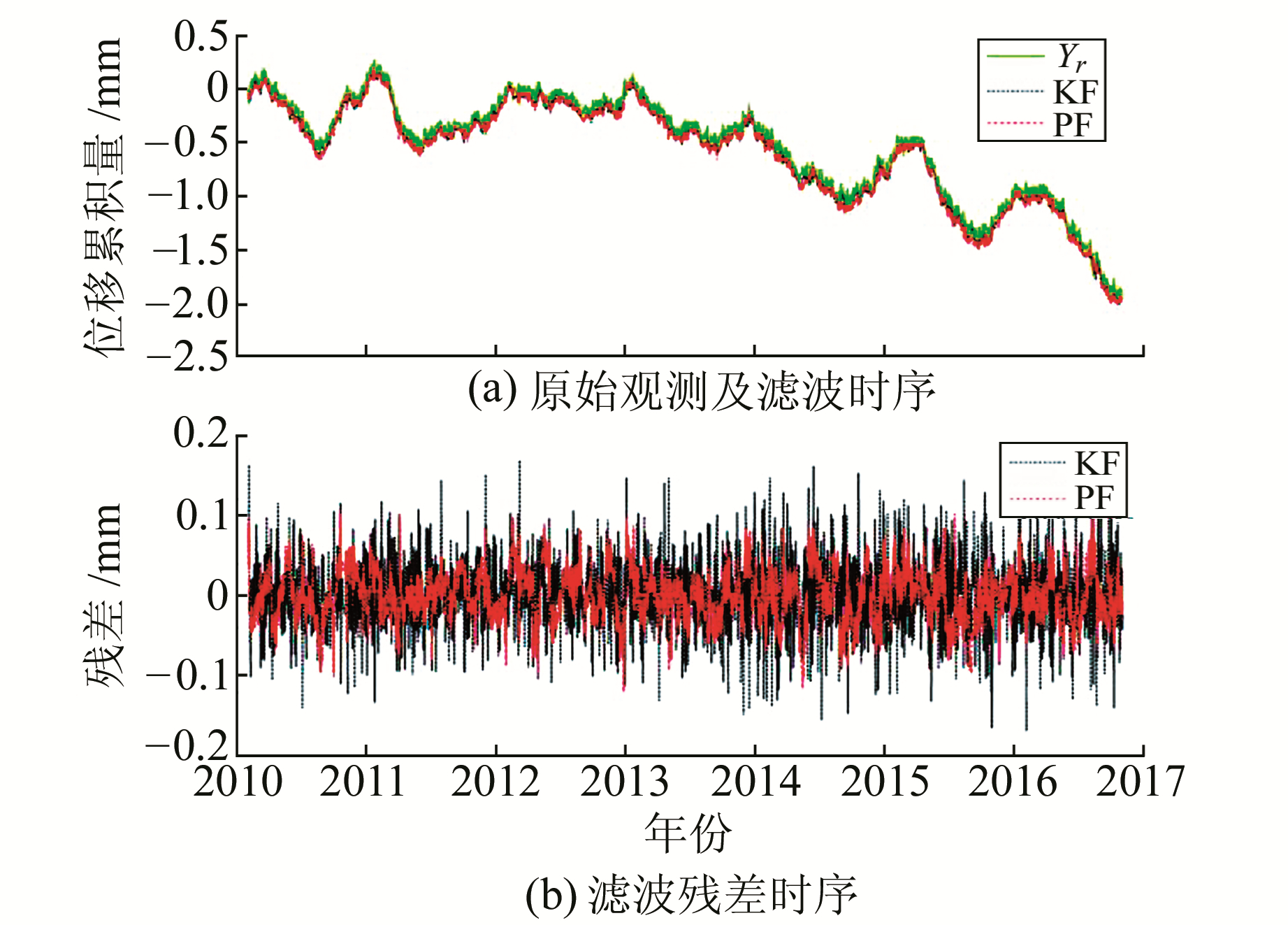
2) 唐山水准3-2。与基线Ⅰ-Ⅱ处理类似,水准3-2的PF和KF结果分别见图 7和表 3。由图 7(a)看出,其整体变化形态呈下降趋势并具一定的周期性,但每年周期形态略有差异:年变幅度不断减小然后逐步增大,2013年之后年周变更明显并伴随下降趋势;2016年年中持续下降,破年变。图 7(b)和表 3表明,PF的精度略优于KF。
|
图 7 唐山水准3-2滤波值及残差值时序 Fig. 7 Filter value and residual sequence diagram of Tangshan leveling line 3-2 |
|
|
表 3 唐山水准3-2滤波残差统计 Tab. 3 Filter residuals of Tangshan leveling line 3-2 |
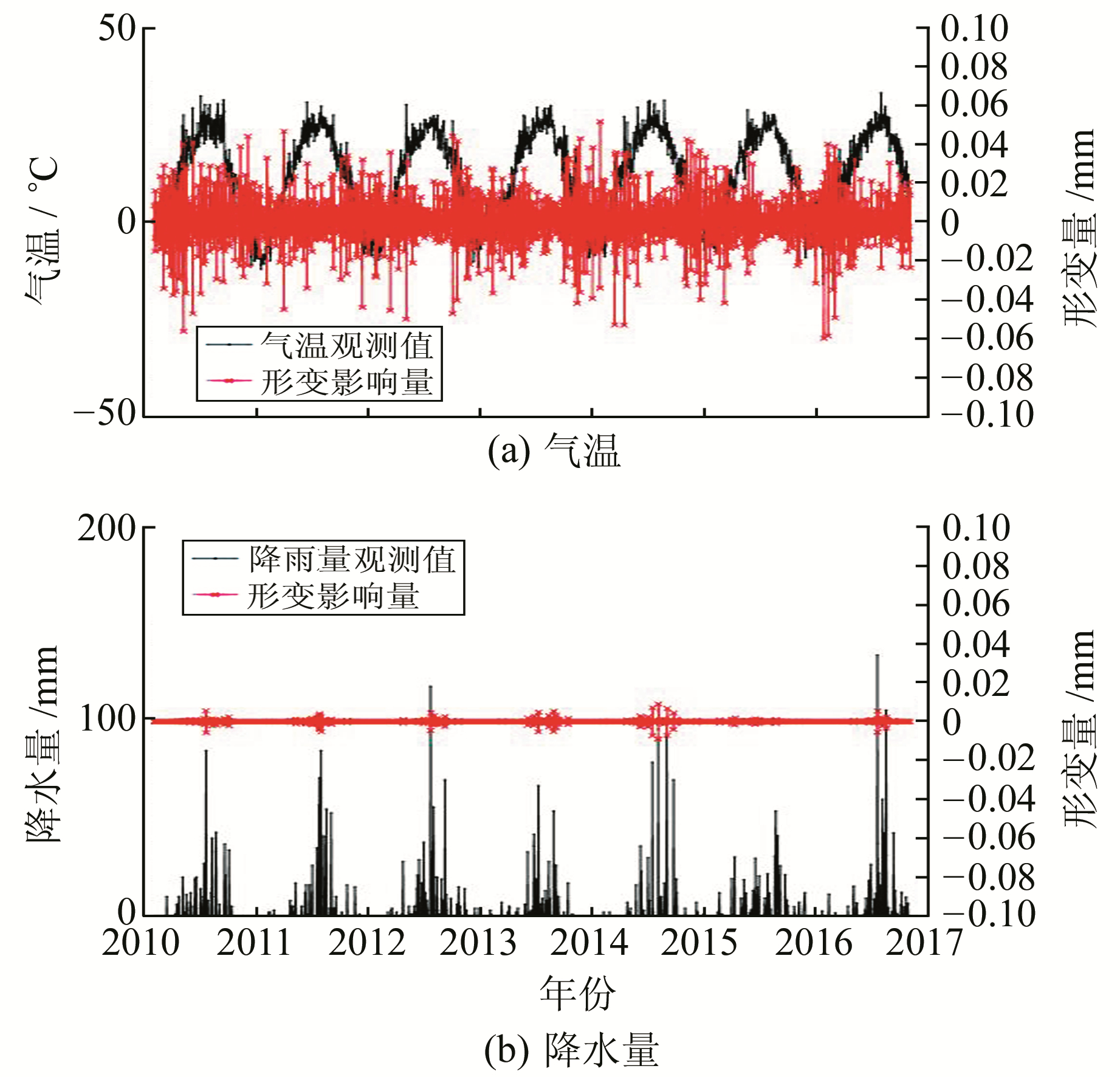
1) 基线Ⅰ-Ⅱ。环境因子(气温、降水量)对基线Ⅰ-Ⅱ跨断层形变观测和断层运动的贡献如图 8和图 9所示。
|
图 8 唐山基线Ⅰ-Ⅱ环境因子及其形变影响 Fig. 8 Environmental observations and their influence on deformation of Tangshan baseline Ⅰ-Ⅱ |

|
图 9 唐山基线Ⅰ-Ⅱ构造形变位移累积量 Fig. 9 Tectonic deformation displacement cumulant of Tangshan baseline Ⅰ-Ⅱ |
由图 8看出,气温对基线Ⅰ-Ⅱ形变观测量的影响较为显著,最大达0.05 mm;降水量的影响较小,约-0.01~0.01 mm,基本可以忽略,与娄关寿等[1]、黄建平等[11]的结论一致。由图 9给出的构造形变位移累积量时序知,2012-05-28河北唐山MS4.7地震、2015-09-14河北昌黎ML4.2地震和2016-09-10河北唐山MS4.1地震(震中距分别为27.2 km、52.2 km、37.4 km)在震前1~2 a内均出现破趋势性变化异常,说明唐山基线Ⅰ-Ⅱ对其周围100 km范围内的4级左右地震具有较好的响应。
2) 水准3-2。环境因子(气温、降水量)对跨断层形变观测和断层运动的贡献结果见图 10和图 11。

|
图 10 唐山水准3-2环境因子及其形变影响 Fig. 10 Environmental observations and their influence on deformation of Tangshan leveling line 3-2 |
|
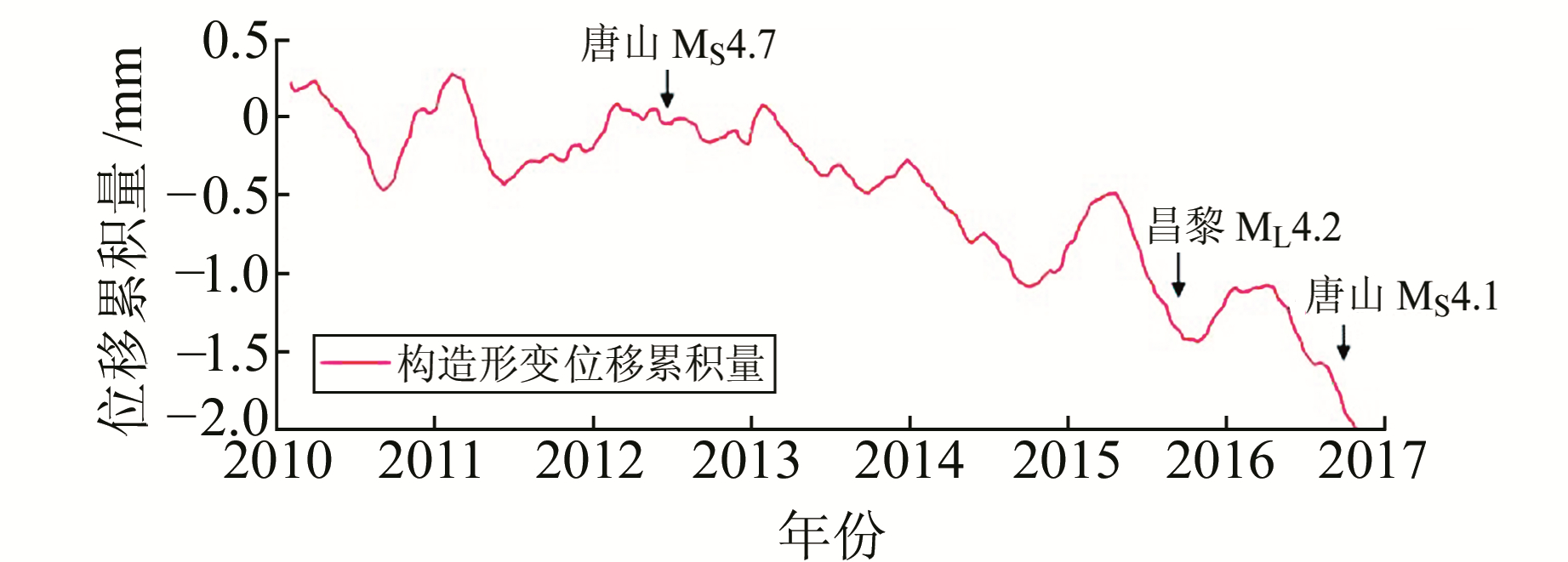
图 11 唐山水准3-2构造形变位移累积量 Fig. 11 Tectonic deformation displacement cumulant of Tangshan leveling line 3-2 |
由图 10看出,气温对水准3-2形变观测量的影响很小,约0.01~0.02 mm,降水量的影响略大,可达0.03 mm。由图 11知,3次地震也在震前1~2 a内出现破趋势性变化异常,说明唐山水准3-2对其周围100 km范围内4级左右地震同样具有较好的响应。
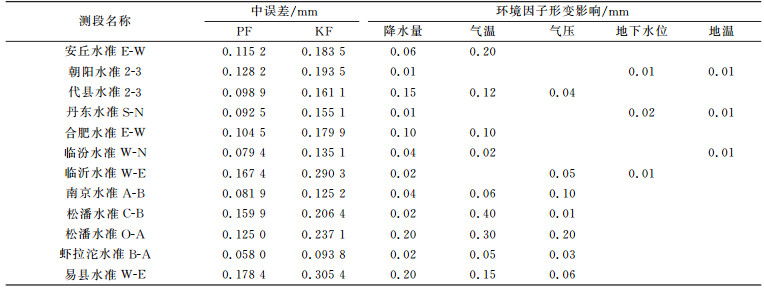
4.3 其他台站与§4.1、§4.2处理方法类似,对其他11个台站(12条测线)进行PF和KF滤波,并对环境因子形变影响进行统计,结果见表 4。
|
|
表 4 滤波残差中误差和环境因子形变影响 Tab. 4 Filter residuals and Environmental influence on deformation of other 11 leveling lines |
由统计结果可知,PF的残差中误差均小于KF。降水量对松潘水准O-A、易县水准W-E的影响较大,约为0.20 mm;气温对松潘水准C-B、松潘水准O-A的影响较大,最大为0.40 mm;气压对松潘O-A的影响最大,为0.20 mm;进行地下水位和地温测量的台站较少,其影响较小,小于0.02 mm。松潘水准O-A形变观测量受降水量、气温、气压的影响较大,松潘水准C-B受气温的影响较大,而朝阳水准2-3和丹东水准S-N受降水量、地下水位等影响均较小。因此,为提取可靠的断层构造运动信息,有必要根据台站的环境特点增加合理的辅助观测。
5 结语1) 采用残差重采样粒子滤波进行跨断层数据处理是可行的,且精度优于卡尔曼滤波。
2) 综合分析跨断层定点台站的水准(基线)观测和降水量、气温等辅助观测数据,可以获取环境因子对形变观测量的影响和断层构造运动信息。
3) 大同水准3-1、唐山基线Ⅰ-Ⅱ和水准3-2对其周围100 km范围内的4级以上地震具有较好的响应,为比较可靠的前兆异常。
4) 不同测线受不同环境因子影响的量级存在一定差异,为获得更为可靠的断层构造运动信息,需要排除环境干扰因素影响,应根据跨断层定点台站的环境特点设置合理的辅助观测手段。
| [1] |
楼关寿, 周伟, 金鹏, 等. 跨断层形变观测干扰因素的调查[J]. 大地测量与地球动力学, 2010, 30(增2): 68-74 (Lou Guanshou, Zhou Wei, Jin Peng, et al. Investigation on Interference Factors of Cross-Fault Deforamation Observation[J]. Journal of Geodesy and Geodynamics, 2010, 30(S2): 68-74)
(  0) 0) |
| [2] |
吴大铭, 韩大宇. 用多道维纳滤波方法处理唐山地震前后的大灰厂三种形变资料[J]. 地震学报, 1983, 5(1): 33-40 (Wu Daming, Han Dayu. Processing Three Kinds of Deformation Data of the Dahuichang Station before and after Tangshan Earthquake by the Multi-Chanel Wiener Filtering Method[J]. Acta Seismol Sin, 1983, 5(1): 33-40)
(  0) 0) |
| [3] |
王金明, 卢良玉. 桃花吐短水准干扰因素的再研究[J]. 东北地震研究, 1998, 14(2): 28-34 (Wang Jinming, Lu Liangyu. Further Research on Interference Factor of Leveling at Taohuatu[J]. Seimological Research of Northeast China, 1998, 14(2): 28-34)
(  0) 0) |
| [4] |
游丽兰, 刘大杰, 黄加纳, 等. 跨断层测量资料的卡尔曼滤波数学模型[J]. 中国地震, 1992, 8(3): 44-52 (You Lilan, Liu Dajie, Huang Jiana, et al. A Mathematical Model of Kalman Filtering for Cross-Fault Measurement[J]. Earthquake Research in China, 1992, 8(3): 44-52)
(  0) 0) |
| [5] |
Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45 DOI:10.1115/1.3662552
(  0) 0) |
| [6] |
李新, 摆玉龙. 顺序数据同化的Bayes滤波框架[J]. 地球科学进展, 2010, 25(5): 515-522 (Li Xin, Bai Yulong. A Bayesian Filter Framework for Sequential Data Assimilation[J]. Advances in Earth Science, 2010, 25(5): 515-522)
(  0) 0) |
| [7] |
Gordon N J, Salmond D J, Smith A F M. Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation[C]. IEE Proceedings F(Radar and Signal Processing), London, 1993 https://ieeexplore.ieee.org/document/210672
(  0) 0) |
| [8] |
Douc R, Cappe O. Comparison of Resampling Schemes for Particle Filtering[C]. International Symposium on Image and Signal Processing and Analysis, Croatia, 2005 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1521264
(  0) 0) |
| [9] |
Zhang H J, Qin S X, Ma J W, et al. Using Residual Resampling and Sensitivity Analysis to Improve Particle Filter Data Assimilation Accuracy[J]. IEEE Geoscience & Remote Sensing Letters, 2013, 10(6): 1 404-1 408
(  0) 0) |
| [10] |
王秀文. 山西断陷带垂直形变特征及其与地震的关系[J]. 地壳形变与地震, 1991, 11(3): 63-68 (Wang Xiuwen. The Characteristics of Vertical Deformation and Its Relationship with Earthquakes in Shanxi Fault Foundering Zone[J]. Crustal Deformation and Earthquake, 1991, 11(3): 63-68)
(  0) 0) |
| [11] |
黄建平, 石耀霖, 孙玉军, 等. 气温变化对唐山地震台跨断层形变观测的影响[J]. 中国地震, 2012, 28(2): 222-230 (Huang Jianping, Shi Yaolin, Sun Yujun, et al. Effect of Air Temperature Variation on the Cross-Fault Deformation Observation at Tangshan Seismic Station[J]. Earthquake Research in China, 2012, 28(2): 222-230)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37