2. 中国科学院地球动力学计算重点实验室, 北京市玉泉路19号甲, 100049
2011-03-11发生的日本东北大地震(MW9.0)是自21世纪以来全球第二大地震,是发生于太平洋板块与北美板块间的典型低角度逆冲型地震。Hayes等[1]利用历史地震目录确定了全球海沟处的板片俯冲几何模型,该模型表明,发生于日本周围的地震大多数分布在较浅的靠近海沟的位置,深度在200 km以上,因此该区域为震间闭锁应力积累区,为大地震易发区域。根据应力积累释放和凹凸体的关系,浅源闭锁处地震的频发同样影响了较深濡滑区域的应力分布,并改变了背景构造应力场,影响到震后的粘滞调整。因此作为研究地震孕育-破裂循环的基础,有必要深刻认识同震变形以及断层滑动分布特征。
该地震发生以后,许多研究机构运用不同的数据和方法给出了不同的同震滑移结果。Yagi和Fukahata[2]利用地震波资料得到滑移分布和地震矩释放速率函数,Lee等[3]利用远震波形、强震和GPS资料得到滑动分布模型,Ozawa等[4]单独利用GPS数据计算断层滑动分布模型,Ozawa等[5]联合GPS和海底GPS计算断层滑动分布模型等。尽管这些断层滑动分布模型给出的震级相似,但同震滑动分布形态各异,其差异原因值得深入研究。
然而,由于远场GPS位移的量级远小于近场,到目前为止,还没有研究者真正意义上把远场GPS同震位移应用在反演断层滑动分布的研究中。我们利用球形地球的位错理论,通过计算和讨论4种基本地震位错源在远场、近场的变形特征,研究远场GPS数据在断层滑动分布中的影响和作用,为后续断层滑动分布反演以及地震位错Love数的反演研究提供理论基础。
1 4种地震位错源的同震变形计算公式地震位错理论可以用来计算地震产生的变形,如位移、大地水准面、重力、倾斜和应变等。对于半无限空间介质模型,人们已经提出了很多理论和计算方法[6-9]。本研究关注远场变形问题,选择合理的位错理论是必要的,以便减少地球曲率和层状构造的影响,所以我们采用Sun等[9]的理论,以保证计算精度。
根据位错理论,我们假设一个球形、非旋转、完全弹性、各向同性(SNREI)的地球模型,在地球内部考虑一个双力偶,则地球变形可以由平衡方程、泊松方程和本构关系描述。这3个基本方程可以利用球函数展开为一个六阶方程组(球型场)和一个二阶方程组(环型场)。利用地球内部各不连续界面的边界条件以及地表面的自由边界条件,就可以解算出地震位错Love数,并由Love数计算出相应的地震变形格林函数。
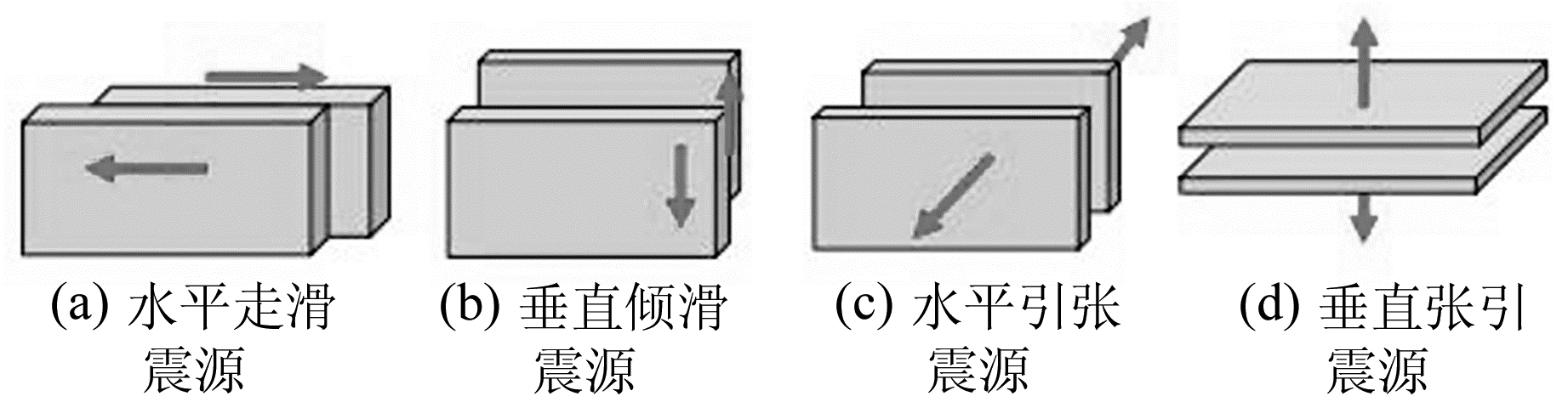
由于地震变形的类型通常可以由震源的3个分量和断层面法矢量的3个分量的组合来表示,例如,一个垂直断层水平滑动时便是其中的组合之一,即走滑断层。这样的组合一共有9个,即应该有9个不同的断层类型,相应的应该有9组不同的位错解,而总变形应该是这9组位错解的组合。然而,由于所采用地球模型的对称性以及坐标轴变化的共轭性,最终完全独立的位错解只有4个。即如果我们能首先给出这4个独立位错解,其组合就可以给出任意断层模型的地震变形解。我们选取下列4个独立震源类型[9]:垂直断层水平走滑破裂(12)、垂直断层上下倾滑破裂(32)、垂直断层水平引张破裂(22)和水平断层垂直引张破裂(33)(图 1),其对应的独立解分别为Y12、Y32、Y22和Y33。
|
图 1 4个独立震源类型 Fig. 1 The schematic of four independent source types |
这4个独立解的组合就可以用来表示一般剪切破裂型地震的一般解Y(s):

|
(1) |
式中,δ和λ分别表示地震断层的倾角和滑动角。本文中我们主要讨论水平位移场,Y(s)代表水平位移的格林函数。
式(1)表明,地震变形的计算除了依赖于4个独立位错解,还依赖于地震断层的倾角和滑动角的变化。地震断层的倾角和滑动角的不同取值代表了不同类型的震源。所以,在下文研究中,将分别考虑这两部分对计算远场地震水平位移的影响,以研究远场地震变形的特征和规律。
2 2011年日本大地震的远场同震位移日本东北部海域于2011-03-11发生了MS9.0低角度逆冲型大地震,是日本有史以来记录到的最大地震。地震发生后,不同研究机构利用不同数据源单独或者联合反演得到不同的断层滑动模型,如地震波数据、大地测量数据[10]、强震数据、海啸数据等。GPS技术作为现代大地测量的有效数据来源,在反演地震断层滑动分布中被广泛应用。日本GeoNet的近场数据显示,东海岸向东最大水平位移为4 m,最大下沉约为1 m。在震中距超过1 000 km的远场,也记录到了超过30 mm和20 mm的显著水平同震位移。
本文所用到的240个GPS同震水平位移由中国地壳运动监测网络和中国周边的国际GPS服务站提供。由于GPS观测本身对垂直位移的精确度没有水平位移高,而且大地震引起的水平位移的量级要远远大于垂直位移,本研究仅选用水平位移场(见图 2,黑色箭头表示实际观测水平位移,白色箭头表示利用球形地球模型的位错理论、Wei等[11]的断层滑动模型计算的远场同震水平位移变化,白色矩形方框内是本文使用的远场数据)。由图 2可见,GPS观测水平位移和理论计算同震水平位移在方向上具有一致性,但理论值略小于实际观测值。这个差异可能来自于两个原因:1)地震断层滑动模型的地震矩被系统性低估;2)位错理论计算中采用的地球模型表层参数所造成[12]。这些远场位移数据为计算断层滑动分布提供了可能。

|
图 2 2011日本东北大地震(MW9.0)远场同震水平位移 Fig. 2 The far-field co-seismic horizontal displacements of 2011 Tohoku-Oki earthquake (MW9.0) |
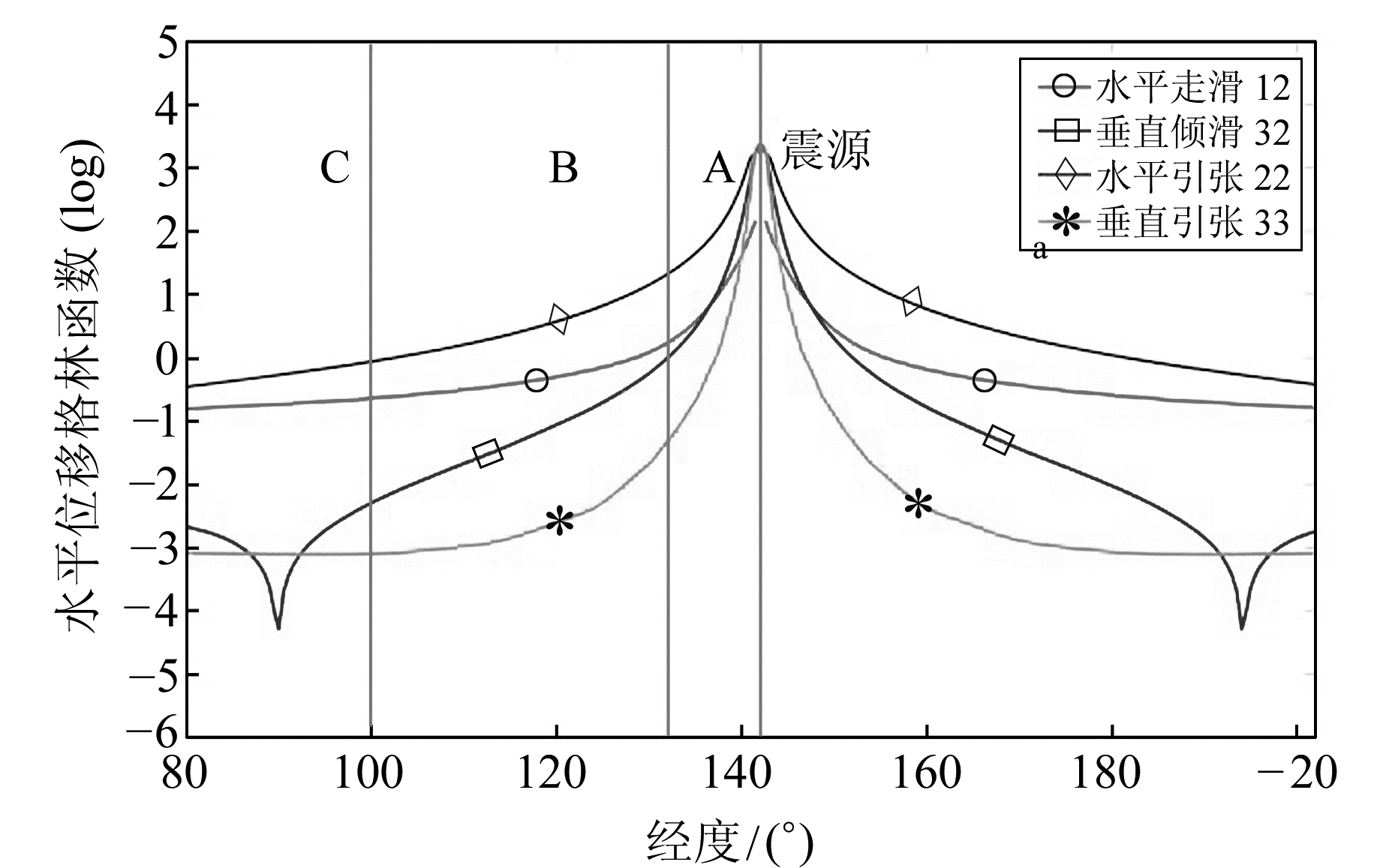
由图 2可以看出,所有远场GPS观测站显示了几乎一致向东的水平位移,并指向震中。最明显的水平位移位于中国东北部、中国北部和朝鲜半岛,其中最大位移32 mm在中国的吉林省。在朝鲜半岛和中国北部分别有24 mm和10 mm的同震水平位移。水平变化迅速向西衰减,并到达中国西部的甘肃和四川。由于GPS观测精度以及远场同震位移的量级越来越小,在2011年日本东北MS9.0大地震GPS观测数据中,距离震中越远,信噪比越差。为了减少低信噪比数据对反演结果精度的影响,本研究排除了信噪比差的观测数据。由于GPS观测点显示的位移一致指向震中方向,水平位移中东方向为主要分量,所以我们以观测点到震中的距离为横坐标,以同震向东方向水平位移为纵坐标,将所有GPS观测点中信噪比大于1的点绘于图 3。图 3中,圆圈表示信噪比大于1的远场GPS观测点,灰色线表示水平位移向东方向的误差,A、B、C分别表示相对于2011日本东北大地震的近场、远场和其他场。水平位移分量随震中距增大呈指数减小[12]。

|
图 3 2011日本东北MW9.0大地震远场同震向东水平位移中信噪比大于1的GPS观测点 Fig. 3 GPS sites of signal-noise ratios greater than 1 of co-seismic horizontal displacement of 2011 Tohoku-Oki earthquake (MW9.0) for far-field |
2011年日本东北大地震发生以后,不同研究机构分别利用地震波数据和大地测量数据给出了断层破裂的尺寸、断层错动方式以及断层滑动分布等信息。大多数研究者在利用GPS数据反演2011日本东北大地震时只用到了日本陆地GPS观测站和海底GPS观测站的数据,相对于远场GPS观测水平位移来说,近场数据在精度、量级和位置上占有较大优势。地震发生以后,利用近场连续GPS观测数据可以马上给出断层参数,并且比地震波数据给出更加吻合的特征。远场GPS观测站同样给出了精度较高的水平位移量,我们将讨论远场水平位移的变形特征及其在断层滑动分布反演中的作用。
式(1)表明,同震位移是4个独立解的组合,并且受到两部分的影响:一部分跟水平位移格林函数有关,是地球介质对地震震源的响应;另一部分跟λ和δ有关,是断层几何形态和滑动方式的影响。两者的乘积共同决定了实际地震同震变形量。本节将以2011年日本东北MS9.0大地震为例,逐一分析各独立解以及倾滑角在远场GPS水平位移中的变形特征。
3.1 4种独立震源的水平位移格林函数的量级比较任意位错源产生的同震变形均可以通过4个独立解的组合得到。首先,我们考虑低角度逆冲型大地震远场位移的4个同震位移格林函数(Y12、Y32、Y22和Y33)的分布特征。以2011日本东北MS9.0大地震点源为例,地震震源位于(38°N, 142°E),震源深度为20 km,令式(1)中Y12、Y32、Y22和Y33的系数均为1,这样就排除了断层几何形态和滑动方式的影响,只考虑地球弹性介质对地震震源的响应,然后分别计算这4组格林函数的值。为此,选择震源所在的纬度圈作为观测计算点,计算并比较4个独立解水平位移的格林函数量级,其结果绘于图 4(A、B、C意义如图 3)。
|
图 4 4个独立震源所对应的水平位移格林函数(对数值) Fig. 4 Green function of horizontal displacement for four independent sources |
由图 4可以看出,在日本地震近场A区,4个独立震源都产生了相对较大的同震水平位移;随着距离的衰减,4组同震位移值也分别减小,但衰减速率各不相同。在B区,水平引张位移格林函数Y22所占比重是其他几项和的5~10倍,即水平走滑分量格林函数Y12、垂直倾滑分量格林函数Y32以及垂直引张分量格林函数Y33都远小于Y22。这些变形特征的产生原因可以理解为:该地震发生于地震活动性显著的太平洋板块与北美板块间的俯冲带上,是典型的板间逆冲型地震。对于这种低角度逆冲型大地震来说,主要是由于断层水平引张产生地面剧烈水平位移,所以不管是在近区还是远区,水平引张分量Y22都是主要变形分量。图 4的有效远场水平位移对应于图 2白色方框里GPS观测水平位移。而对于C区至更远的区域,分量Y22和Y12交替占主要变形量,但对于2011年日本东北大地震来说,大于4 000 km观测到的GPS同震位移几乎为0。式(1)中,Y22和Y33是耦合在一起的,但在B区Y33的值远小于Y22的大小。因此,日本MS9.0地震远场区同震水平位移主要是由水平位移格林函数Y22的大小决定的。同样,2004年苏门答腊MS9.1地震、2010年智利MS8.8地震也属于这种低角度逆冲型地震。距离震源7°~42°的GPS同震水平位移可以作为低倾角俯冲型地震对反演断层滑动分布影响最主要的远场距离。
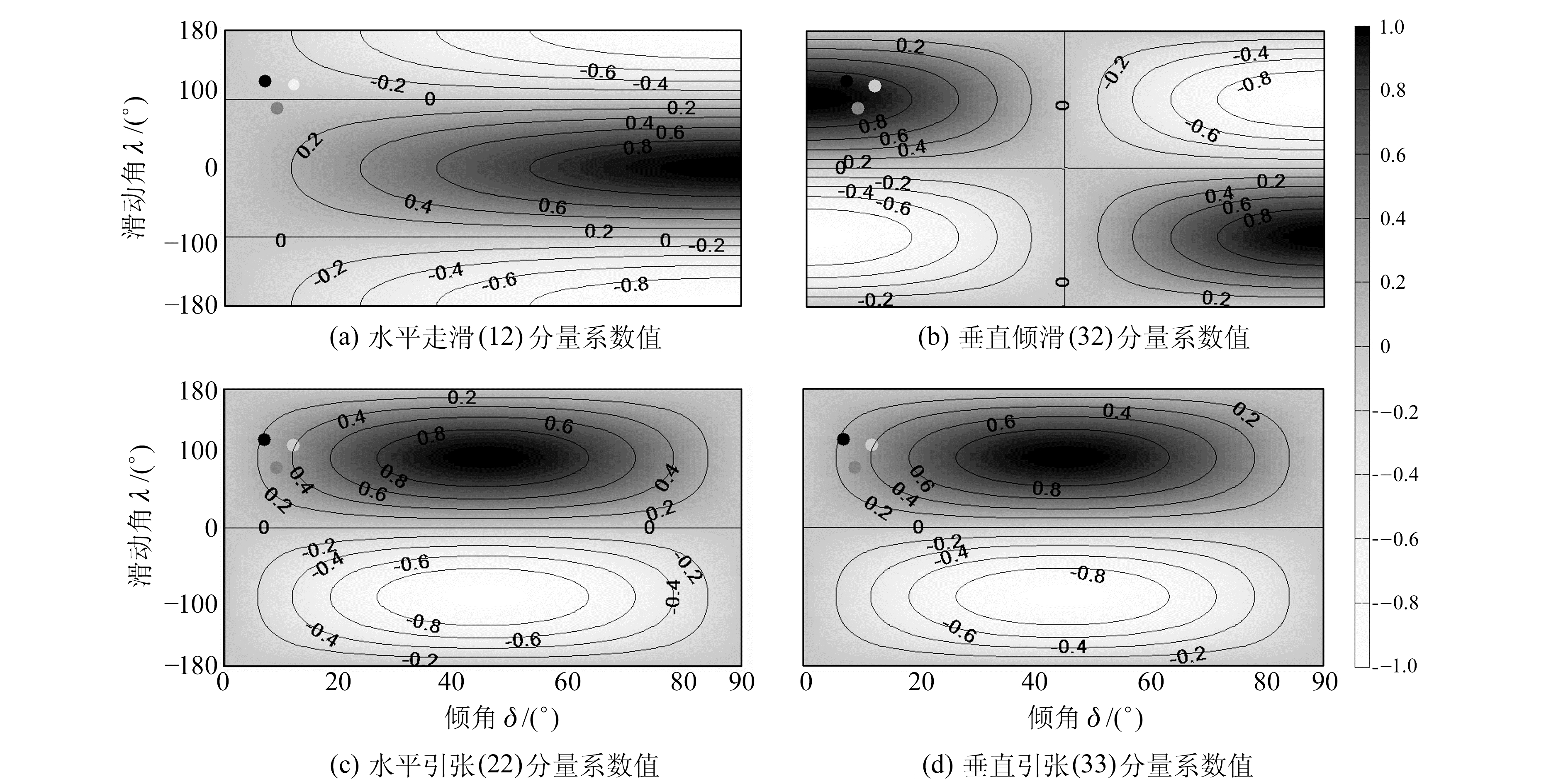
3.2 断层倾角和滑动角的影响§3.1只考虑了4个独立震源水平位移解的格林函数在远场GPS数据中的影响,同样,我们也需要考虑4组解的系数对应不同倾角δ和滑动角λ的变化。假设倾角δ取值范围为[0~90°],滑动角λ的取值范围是[-180°~180°]。图 5中深灰色、黑色和浅灰色点分别表示低角度逆冲型地震2011年日本东北MS9.0大地震、2004年苏门答腊MS9.1地震和2010年智利MS8.8地震。如图中等高线所示,对于上述低角度逆冲型地震,垂直引张量Y22的系数值明显大于水平引张量Y12的系数值,而且对于这类地震,垂直倾滑格林函数和垂直引张格林函数要远小于这两项,所以不予考虑。结合格林函数和系数的乘积,对于低角度逆冲型地震,结合§3.1的分析,远场GPS水平位移明显受sinλsin2δY22的影响。
|
图 5 4个独立解水平位移的系数值 Fig. 5 The coefficient of horizontal displacement for four independent sources |
根据全球构造板块学说,地壳被一些构造活动带分割为彼此相对运动的板块:太平洋板块、欧亚板块、非洲板块、印度洋板块和南极板块。全球大部分地震发生在大板块的边界上,另一部分发生在板块内部的活动断裂上。最主要的地震带分布在环太平洋地震带上,包括南美洲的智利、秘鲁,北美洲的危地马拉、墨西哥、美国等国家的西海岸以及菲律宾、印度尼西亚和新西兰等国家和地区。该地震带地震活动最强烈、最集中,全球约80%的地震都发生在这里,集中了全世界80%以上的浅源地震(0~70 km)、90%的中源地震(70~300 km)和几乎全部的深源地震(300~700 km)。
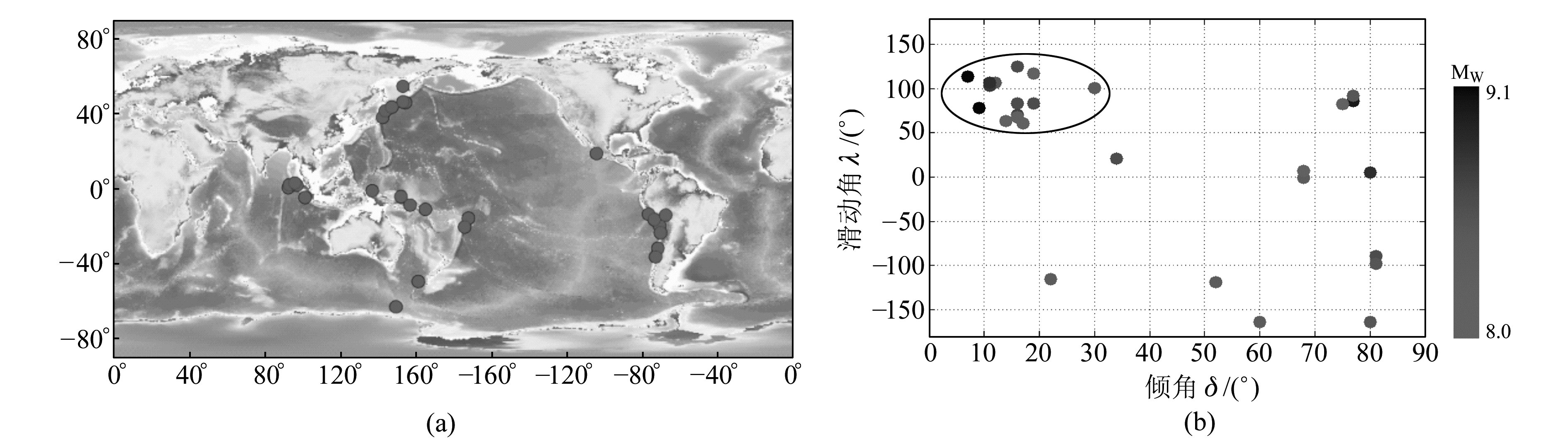
根据USGS收录的地震目录,我们统计了全球1990年以来大于8.0级的地震共27个(图 6(a))。由于地球上板块之间相互挤压碰撞,造成板块边沿及板块内部产生错动和破裂,所以大部分地震发生在板块交界处(图 6(a))。大部分大于8.0级的大地震发生在环太平洋地震带上,包括2004年苏门答腊MS9.1地震、2010年智利MS8.8地震和2011年日本东北MS9.0地震等。
|
图 6 1990年以来全球27个MW8.0以上地震 Fig. 6 Earthquakes greater than MW8.0 in the global since 1990 |
如图 6(b)所示,全球绝大多数产生较大自然灾害的大地震集中于低倾角高滑动角的区域,只有小部分是高倾角零散分布的地震。黑色椭圆中包含了大多数的低角逆冲型大地震,包括2004年苏门答腊MS9.1地震、2010年智利MS8.8地震和2011年日本东北MS9.0地震,它们都是浅部破裂的大地震,并引发了巨大的海啸。
因此,对于这种低角逆冲型大地震,我们可以选择离震中7°~42°的远场范围内的GPS水平位移,通过约束sinλsin2δY22项来联合反演断层滑动分布。
5 结语本文以2011年日本东北MS9.0大地震为例,利用球形地球模型的位错理论研究远场GPS同震位移的变形特征,为联合远场GPS数据和近场GPS数据反演断层滑动分布作理论准备,并为利用远场GPS数据反演位错Love数(h和l)提供理论依据。
由地震位错理论可知,任意震源产生的同震变形均可以通过水平走滑震源、垂直倾滑震源、水平引张震源和垂直引张震源的组合得到。地震产生的同震位移不仅与4组同震位移格林函数有关,还与地震的类型有关。对于绝大多数大型俯冲型地震来说,同震位移格林函数Y22占主要分量。通过4组位移格林函数的量级比较,在距离震中7°~42°的远场GPS观测站的水平位移,可以用来约束地震的断层滑动分布。在以后的研究中,对于不同形态的地震,无论是高倾角还是低倾角,同样可以利用以上的分析思路来研究4组分量中占远场主要成分的分量,分析地震的破裂形态。我们的研究结果提供了采用远场GPS水平位移反演低角度逆冲型地震断层滑动分布的新思路:远场数据和近场数据可以同时用来约束水平引张震源sinλsin2δY22,而近场数据可以继续约束其余3项。
Yang等[13]利用GRACE重力卫星反演了地震位错Love数(k),得到可以反映区域构造的地震变形特征数,反映了局部地球模型参数与全球平均值的差异。根据同样方法,利用GPS观测数据也可以反演得到其他位错Love数。所以,基于本文的研究结果,利用远场GPS数据反演出反映区域构造的位错Love数h22和l22,使其更加接近真实的地球模型。这样,就可以利用GRACE和GPS观测得到一套完整的反映区域构造的地震位错Love数以及相应的格林函数,为地震断层反演提供理论依据。
| [1] |
Hayes G P, Wald D J, Johnson R L. Slab1.0: A Three-Dimensional Model of Global Subduction Zone Geometries[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B1): 180-198
(  0) 0) |
| [2] |
Yagi Y, Fukahata Y. Rupture Process of the 2011 Tohoku-Oki Earthquakeand Absolute Elastic Strain Release[J]. Geophys Res Lett, 2011, 38: L19 307
(  0) 0) |
| [3] |
Lee S J, Huang B S, Ando M, et al. Evidence of Large Scale Repeating Slip during the 2011 Tohoku-Oki Earthquake[J]. Geophys Res Lett, 2011, 38: L19 306
(  0) 0) |
| [4] |
Ozawa S, Nishimura T, Suito H, et al. Coseismic and Postseismic Slip of the 2011 Magnitude-9 Tohoku-Oki Earthquake[J]. Nature, 2011, 475: 373-376 DOI:10.1038/nature10227
(  0) 0) |
| [5] |
Ozawa S, Nishimura T, Munekane H, et al. Preceding, Coseismic, and Postseismic Slips of the 2011 Tohoku Earthquake, Japan[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B7): 346-348
(  0) 0) |
| [6] |
Okada Y. Surface Deformation Caused by Shear and Tensile Faults in a Half-Space[J]. Bull Seism Soc Am, 1985, 75(4): 1 135-1 154
(  0) 0) |
| [7] |
Sun W, Okubo S. Surface Potential and Gravity Changes due to Internal Dislocations in Aspherical Earth-Ⅰ. Theory for a Point Dislocation[J]. Geophys J Int, 1993, 114: 569-592 DOI:10.1111/gji.1993.114.issue-3
(  0) 0) |
| [8] |
Sun W, Okubo S. Effects of Earth's Spherical Curvature and Radial Heterogeneity in Dislocation Studies-For a Point Dislocation[J]. Geophysical Research Letters, 2002, 29(12): 46-1-46-4
(  0) 0) |
| [9] |
Sun W, Okubo S, Fu G, et al. General Formulations of Global Co-Seismic Deformations Caused by an Arbitrary Dislocation in a Spherically Symmetric Earth Model:Applicable to Deformed Earth Surface and Space-Fixed Point[J]. Geophys J Int, 2009, 177: 817-833 DOI:10.1111/gji.2009.177.issue-3
(  0) 0) |
| [10] |
Diao F Q, Xiong X, Zheng Y. Static Slip Model of the MS9.0 Tohoku (Japan) Earthquake: Results from Joint Inversion of Terrestrial GPS Data and Seafloor GPS/Acoustic Data[J]. Chin Sci Bull, 2012, 57: 1 990-1 997 DOI:10.1007/s11434-012-5014-5
(  0) 0) |
| [11] |
http://www.tectonics.caltech.edu/slip_history/2011_taih-eiyo-oki/ (last accessed 2012 January 20)
(  0) 0) |
| [12] |
Wang W, Sun W, Wu Y, et al. Modification of Fault Slip Models of the MS9.0 Tohoku Earthquake by Far Field GPS Observations[J]. Journal of Geodynamics, 2014, 75: 22-33 DOI:10.1016/j.jog.2014.01.005
(  0) 0) |
| [13] |
Yang J, Zhou X, Yi S, et al. Determining Dislocation Love Numbers using GRACE Satellite Mission Gravity Data[J]. Geophysical Journal International, 2015, 203(1): 257-269 DOI:10.1093/gji/ggv265
(  0) 0) |
2. Key Laboratory of Computational Geodynamics, A19 Yuquan Road, Beijing 100049, China
 2017, Vol. 37
2017, Vol. 37


