2. 中国科学院计算地球动力学重点实验室, 北京市玉泉路19号甲, 100049
地震发生在断层上,断层的破裂会辐射地震波,并引起地壳变形和地球物质迁移。震源力可以用位错/位移间断来描述。位错理论是现代地震学的重要理论支柱,是模拟同震变形、震后变形以及地震波形的重要物理工具。通过位错理论计算格林函数,并利用大地测量或地震学观测数据反演震源参数和滑移是研究地震破裂、构造地质等方面的重要手段[1-2]。随着重力卫星GRACE能够观测到全球特大地震,位错理论模型在解释卫星观测信号以及利用同震重力变化确定震源参数的研究中也起着重要作用[3-7]。
自Steketee[8]将位错理论引入地震学后,大量学者研究了均匀半无限空间地球模型下的同震变形问题。Okada[9]总结整理了前人的工作,并给出了点源和矩形断层的解析公式,可以用于计算任意剪切或引张断层在均匀半空间下引起的同震地表位移、应变和倾斜,解析公式简洁实用、计算效率高,广泛应用于地震断层参数和滑移分布的反演问题。陈运泰等[10-11]讨论了结合半无限空间位错理论和地表形变资料进行震源反演的一般方法,并利用实际观测数据反演了1966年邢台地震和1976年唐山地震的震源过程。Rundle[12]利用贝塞尔函数得到了无自重的层状半无限空间的同震变形。Okubo[13]推导并给出了弹性均匀半无限空间的同震重力变化,与Okada相似,该理论模型也是简洁的解析公式。基于Takeuchi等[14]给出的地震球面波理论,Sun等[15-20]利用龙格-库塔数值方法解决了在一个球对称的分层地球模型下,由内部位错源引起的地表位移、应变、重力和垂线偏差的变化。研究表明,当震源距超过10°,地球曲率的影响可达10%;震源距大于0.5°时,需要考虑地球径向的不均匀性[18]。Okubo[21]提出了互易定理,将位错解与潮汐、剪切力、负荷变形的解联系在一起,即一个内部位错源引起的地表变形可以用在该深度的潮汐解、剪切力解和负荷解线性表示。Pollitz[22]给出了无自重层状球形地球的同震位移。基于Rundle和Okada的理论模型,Wang等[23]发展了分层半无限空间的位错理论,并采用传递矩阵的方法得到地表的同震变形。郝金来等[24]使用了梯形积分和Filon积分相结合的方法得到了分层介质地球模型的同震位移、应力和应变,加快了计算速度。Fu等[25]在Sun等[15]的球体位错理论基础上,利用微扰原理研究了球形地球横向不均匀性对同震变形的影响。
将弹性位错理论进行扩展可以得到震后黏弹性变形。对黏弹性本构关系经过Laplace变换后得到与弹性问题相同的形式,按照弹性位错方程的解法得到Laplace域的变形,再对其进行Laplace反变换得到震后黏弹性变形。Rundle[26]考虑了一个更接近真实地球的自重、分层半无限空间模型,给出了矩形推覆断层引起的黏弹性变形。Pollitz[27]解决了在一个黏弹性、无自重的球形地球模型下,由位错源引起的区域同震位移场和应变场。Piersanti等[28]、Sabadini等[29]给出了自重、不可压缩、层状球形地球下,位错源引起的地表震后黏弹性变形。另外,多位学者给出了计算有限分层数的震后黏弹变形方法[30-31]。Tanaka等[32]利用复平面路径积分的方法解决了有限层数问题。Wang等[33]利用虚轴积分给出了自重、可压缩、分层半无限空间的黏弹性变形,并给出了一套实用的计算程序。
径向一维分层地球模型下的弹性、黏弹性位错理论都较成熟,但以上研究工作都基于前人给出的经典理论方程的解,并未重新给出基本解。为了方便相关领域研究人员理解和使用球体位错理论模型,本文给出不同物理前提条件下的均匀球变形方程的基本解。
1 物理方程对于无自重的、非自转的地球模型,平衡方程可以写为:
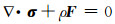
|
(1) |
式中,ρ为介质密度,σ为应力张量,F为外力。如果只考虑弹性地球介质,根据胡克定律,应力应变关系为:
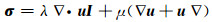
|
(2) |
式中,u为位移矢量,λ和μ为拉梅常数,后者也是剪切模量或刚度,I为单位矩阵,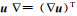

|
(3) |
将式(3)代入式(1)中,并运用:
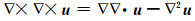
|
(4) |
可得:
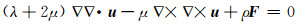
|
(5) |
考虑地球的自重,假设无变形的地球是球对称的,并处于静水平衡状态,初始压力可以写为:
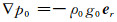
|
(6) |
令r0和r表示变形体的初始位置和变形后的位置,则与位移有如下关系:
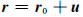
|
(7) |
且初始平衡应力为:
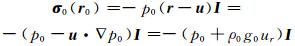
|
(8) |
其散度为:

|
(9) |
另一方面,变形后的密度为:

|
(10) |
故密度增量为:

|
(11) |
变形体的引力位为初始引力位和扰动位之和:

|
(12) |
初始引力位的梯度为正常重力,即

|
(13) |
将式(9)、(13)代入式(1)中,并考虑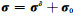

|
(14) |
式中,σδ为应力变化,FD为位错力源。考虑到并不引起混淆,此后用σ替代σδ。将式(9)、(13)代入式(5)中,得到平衡方程的另一种形式:

|
(15) |
另外,在球体内部的扰动位满足泊松方程:

|
(16) |
本文考虑的地球模型是均匀的、非自转的和球对称的模型,故需要考虑§1得到的平衡方程(15)和泊松方程(16)在球坐标(r, θ, λ)下的解。首先,将位移、应力和引力位表达为球谐函数形式。对于矢量场,可以分解为球型和环型的多极表达,位移和法向应力矢量可以写为:
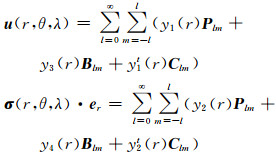
|
(17) |
式中,
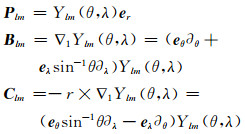
|
(18) |
式中,
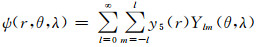
|
(19) |
为了得到方程的解,除了上述未知变量(y1(r), y2(r)~y5(r))之外,还需引入另一个新变量[14]:
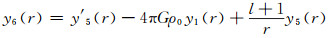
|
(20) |
引力位在地球内部满足泊松方程(16),在地表满足拉普拉斯方程。地表处的边界条件较为复杂,而y6(r)在地表为0,该变量的引入将对后面利用边界条件得到方程的通解系数提供方便。同引力位的展开,将体积变化作球谐展开得:
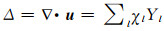
|
(21) |
且χl和y1、y3有如下关系:

|
(22) |
平衡方程(14)可以分为两个分别关于er和eθ的方程,略去繁琐的数学过程,直接给出这两个方程的化简结果:
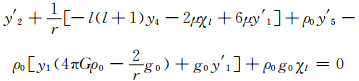
|
(23) |

|
(24) |
同理,弹性本构关系方程(2)在球坐标下表示为:
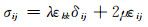
|
(25) |
式中,δij为狄拉克符号,应变分量的球坐标表达为:
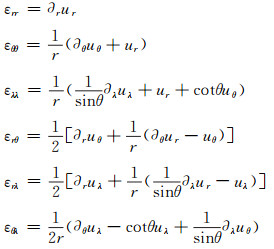
|
(26) |
同样,略去数学过程,得到以下两个微分方程:
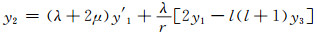
|
(27) |

|
(28) |
由泊松方程可得一个二阶微分方程:
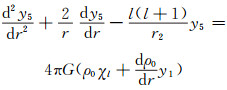
|
(29) |
联合式(20)~(24)以及式(27)~(29),并考虑可压缩的(χl≠0)一般形式,可得关于y1(r)~y6(r)的一阶齐次微分方程组:
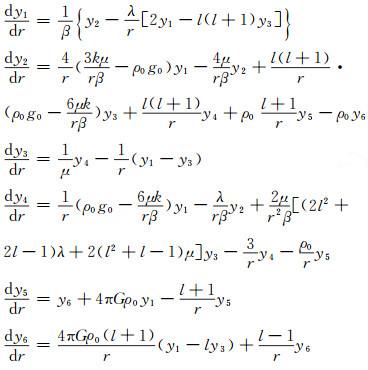
|
(30) |
式中,记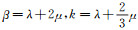
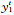
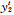
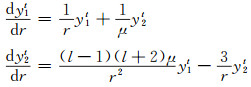
|
(31) |
需要指出的是,式(30)和(31)给出的都是齐次方程组,不包括位错力项。对于一个非齐次方程组,其解的构成是齐次方程组的通解与非齐次项的特解。非齐次项也可以通过边界条件解决,即位错变形的解可以通过方程组(30)和(31)的通解在地表和位错间断面满足边界条件得到,故这里主要考察齐次方程组的解。
3 均质球下的基本解本节将在不同的物理简化假设下给出变形方程在均质球的基本解,首先讨论不同地球模型的球型解,最后给出环型解。
3.1 无自重的地球模型首先,假设地球模型无自重,平衡方程中的G、ψ和g0均消失,同时泊松方程消失。式(30)中关于y5和y6项消失后,6个球型一阶微分方程退化为4个:

|
(32) |
通过数学运算,容易得到上述方程组的解:
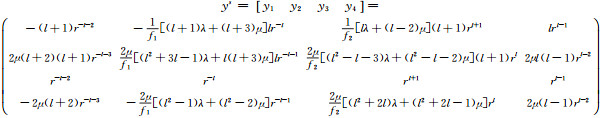
|
(33) |
式中,f1=(l-2)λ+(l-4)μ,f2=(l+3)λ+(l+5)μ。不考虑自重情况下的解为rl和r-l的函数,式(33)中矩阵的逆可以解析得到。通过传递矩阵方法将球心处的解和地表解分别传递到位错间断面的下、上表面,满足位错简单条件和地表处自由表面边界条件得到通解的系数。鉴于解的便利性,该模型在计算同震位移时应用广泛。
3.2 不可压缩的地球模型在短时间尺度上,地球的体积因外力作用发生变化;在长时间尺度上,变形地球可以近似认为体积不变,即不可压缩介质。不可压缩的地球模型是模拟冰川均衡调整、长时间尺度的震后黏弹性变形等地球物理问题的经典模型。当体积不变时,χl=0,密度为常数∂rρ0=0,故由式(11)可知密度增量为0,即Δρ=0。此时,平衡方程(14)和泊松方程(16)解耦,且泊松方程退化为拉普拉斯方程。仅考虑齐次方程形式,有:

|
(34) |
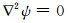
|
(35) |
对于不可压缩介质,令
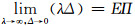
|
(36) |
故在不可压缩条件下,本构关系式(3)为:
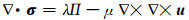
|
(37) |
将式(37)代入式(34)中得到:
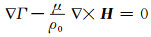
|
(38) |
式中,
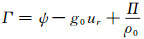
|
(39) |
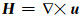
|
(40) |
将Γ和H在球坐标系展开:
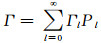
|
(41) |

|
(42) |
将式(41)、(42)作用在式(38)得:
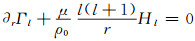
|
(43) |
一方面,对式(38)取散度,并使用
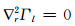
|
(44) |
式中,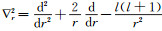

|
(45) |
同理,方程(35)的解为:
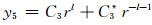
|
(46) |
顾及χl=0,由式(22)可得:
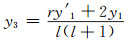
|
(47) |
另一方面,结合式(40)可得:

|
(48) |
联合式(43)、(45)和(48)可得y1的解:
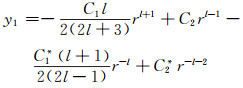
|
(49) |
代入式(47)可得y3的解:

|
(50) |
将y1和y3代入式(28)可得到y4:
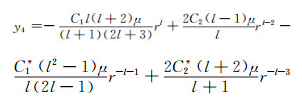
|
(51) |
由应力-应变关系得:

|
(52) |
将式(45)和(49)代入可得y2的解:

|
(53) |
最后得到y6:
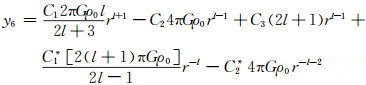
|
(54) |
至此,得到了自重、不可压缩、球对称的均质地球模型的解,式中(C1, C2, C3, 
当自重效应和压缩性无法忽略时,平衡方程(15)和泊松方程(16)耦合,且可以化为6个一阶微分方程组(30),其解较无自重模型和不可压缩模型复杂。同上,在均质球下,密度为常量,即∂rρ0=0。对平衡方程(15)的齐次方程两边取旋度,有:
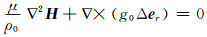
|
(55) |
式中,H定义见式(40)。另一方面,对方程(15)两边取散度,并整理后有:

|
(56) |
将球谐展开式代入式(55)、(56),得:
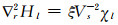
|
(57) |
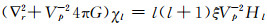
|
(58) |
式中,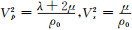



|
(59) |
式中,
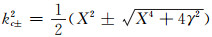
|
(60) |
则式(59)可以写为:
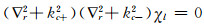
|
(61) |
该方程可以化为2个Helmholtz方程,得到4个独立的解:
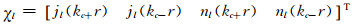
|
(62) |
式中,jl(kr)、nl(kr)(k=kc±)分别是第一类和第二类球贝塞尔函数,jl(kr)在r=0处正则,在r=∞处奇异;nl(kr)与之相反。不失一般性,下面将jl(kr)和nl(kr)统一用fl(kr)表示,求出自重、可压缩的均质球变形方程的基本解。设:

|
(63) |
将其和式(62)一并代入到方程(57)中,可以求得:

|
(64) |
另一方面,顾及χl和Hl的定义式(22)以及
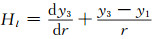
|
(65) |
可得:
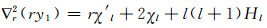
|
(66) |
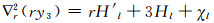
|
(67) |
进一步,利用关系rf′l(kr)=lfl(kr)-krfl+1(kr),式(66)、(67)写为:

|
(68) |
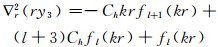
|
(69) |
假设ryr=C1fl(kr)+C2rfl+1(kr),并利用球贝塞尔函数的递推关系:
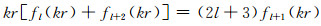
|
(70) |
可得到y1的解为:

|
(71) |
式中,

|
(72) |
相似地,可得y3的解为:

|
(73) |
再将y1和y3代入式(27)、(28)中,得到y2和y4:

|
(74) |
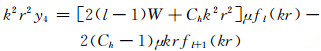
|
(75) |
式(74)中,β=λ+2μ,与前文定义一致。
泊松方程可以写为:
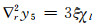
|
(76) |
可以求得y5的解:
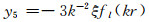
|
(77) |
最后,由式(20)得到y6的解:
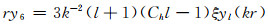
|
(78) |
由于k=kc±以及fl(kr)=(jl(kr), nl(kr)),上述过程可以得到4组关于y1、y2、y3、y4、y5、y6的解。另外,可以容易得到二组解:
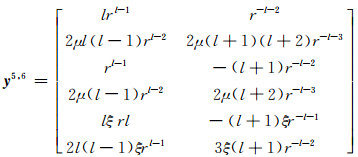
|
(79) |
相对于复杂的球型方程,环型方程(31)较为简单。该方程没有重力项和体积变化项,故在任何物理假设条件下,其解均为:

|
(80) |
本文回顾了位错引起的地球变形和引力位变化的方程,并给出了非自转、球对称、各向同性的均质球下的基本解。
1) 对于无自重的地球模型,不考虑引力位的改变,6个一阶微分方程组退化为4个,其球型解为关于rl和r-l-1的函数。
2) 对于不可压缩的地球模型,体积不变,平衡方程和泊松方程解耦,其球型解同样为rl和r-l-1的函数。
3) 对于顾及自重和可压缩性的模型,其球型解除了2组分别关于rl和r-l-1的函数外,还有4组关于特殊函数jl(kr)和nl(kr)的解。
4) 环型解的形式为关于rl和r-l-1的函数。
在这些解中,rl和jl(kr)在球心处正则,无穷远处奇异;r-l-1和nl(kr)在球心处奇异,无穷远处正则。
以上3种一维地球模型各有用处,例如,鉴于无自重均质球模型的简易性,可以用于与半无限空间模型比较研究地球的曲率效应[34];不可压缩模型可以用于近似模拟长时间尺度的震后变形[28];自重、可压缩的球体模型可以用于模拟完整的同震和震后变形、重力场变化[19, 32]。
在实际计算地球因内部位错引起的变形时,需要考虑分层效应。此时,微分方程组(30)和(32)中与地球材料有关的参数不再是常数,而是随着深度改变。无论如何,在某一分层上,这些参数仍然可以视为常数,满足微分方程组,故解的形式为本文给出的基本解。对于无自重和不可压缩的地球模型而言,基本解为简单的解析解,组成的矩阵的逆同样可以解析得到,故可以通过矩阵传递的方法,满足地表自由边界条件和位错间断条件,求出待定系数。对于自重可压缩的地球模型而言,基本解含有球贝塞尔函数,难以解析得到逆矩阵。可以通过龙格-库塔方法将微分方程组(30)的通解从球心处积分到地表,再将位错的特解从位错间断面积分到地表,共同满足地表自由边界条件得到待定系数。
| [1] |
Zhou X, Cambiotti G, Sun W K, et al. The Coseismic Slip Distribution of a Shallow Subduction Fault Constrained by Prior Information: The Example of 2011 Tohoku (MW 9.0) Megathrust Earthquake[J]. Geophys J Int, 2014, 199(2): 981-995 DOI:10.1093/gji/ggu310
(  0) 0) |
| [2] |
Wang Z, Kato T, Zhou X, et al. Source Process with Heterogeneous Rupture Velocity for the 2011 Tohoku-Oki Earthquake Based on 1-Hz GPS Data[J]. Earth, Planets and Space, 2016, 68(1): 193
(  0) 0) |
| [3] |
Zhou X, Sun W K, Zhao B, et al. Geodetic Observations Detecting Coseismic Displacements and Gravity Changes Caused by the MW=9.0 Tohoku-Oki Earthquake[J]. J Geophys Res, 2012, 117(B5)
(  0) 0) |
| [4] |
Sun W K, Zhou X. Coseismic Deflection Change of the Vertical Caused by the 2011 Tohoku-Oki Earthquake (MW9.0[J]. Geophys J Int, 2012, 189(2): 937-955 DOI:10.1111/gji.2012.189.issue-2
(  0) 0) |
| [5] |
Han S C, Sauber J, Riva R. Contribution of Satellite Gravimetry to Understanding Seismic Source Processes of the 2011 Tohoku-Oki Earthquake[J]. Geophys Res Lett, 2011, 38(24)
(  0) 0) |
| [6] |
Cambiotti G, Bordoni A, Sabadini R, et al. GRACE Gravity Data Help Constraining Seismic Models of the 2004 Sumatran Earthquake[J]. J Geophys Res, 2011, 116(B10)
(  0) 0) |
| [7] |
Cambiotti G, Sabadini R. Gravitational Seismology Retrieving Centroid-Moment-Tensor Solution of the 2011 Tohoku Earthquake[J]. J Geophys Res, 2013, 118(1): 183-194 DOI:10.1029/2012JB009555
(  0) 0) |
| [8] |
Steketee J A. On Volterra's Dislocations in a Semi-Infinite Elastic Medium[J]. Canadian Journal of Physics, 1958, 36(2): 192-205 DOI:10.1139/p58-024
(  0) 0) |
| [9] |
Okada Y. Surface Deformation Caused by Shear and Tensile Faults in a Half-Space[J]. Bull Seism Soc Am, 1985, 75(4): 1 135-1 154
(  0) 0) |
| [10] |
陈运泰, 林邦慧, 林中洋, 等. 根据地表形变的观测研究1966年邢台地震的震源过程[J]. 地球物理学报, 1966, 18(3): 164-181 (Chen Yuntai, Lin Banghui, Lin Zhongyang, et al. The Focal Mechanism of the 1966 Xingtai Earthquake as Inferred from the Ground Deformation Observations[J]. Acta Gephysica Sinica, 1966, 18(3): 164-181)
(  0) 0) |
| [11] |
陈运泰, 林邦慧, 王新华, 等. 用大地测量资料反演的1976年唐山地震的位错模式[J]. 地球物理学报, 1979, 22(3): 201-215 (Chen Yuntai, Lin Banghui, Wang Xinhua, et al. A Dislocation Model of the Tangshan Earthquake of 1976 from the Inversion of Geodetic Data[J]. Acta Gephysica Sinica, 1979, 22(3): 201-215 DOI:10.3321/j.issn:0001-5733.1979.03.001)
(  0) 0) |
| [12] |
Rundle J B. Static Elastic-Gravitational Deformation of a Layered Half Space by Point Couple Sources[J]. J Geophys Res, 1980, 85(B10): 5 355-5 363 DOI:10.1029/JB085iB10p05355
(  0) 0) |
| [13] |
Okubo S. Gravity and Potential Changes Due to Shear and Tensile Faults in a Half-Space[J]. J Geophys Res, 1992, 97(B5): 7 137-7 144 DOI:10.1029/92JB00178
(  0) 0) |
| [14] |
Takeuchi H, Saito M. Seismic Surface Waves[J]. Methods Comput Phys, 1972, 11: 217-295
(  0) 0) |
| [15] |
Sun W K. Potential and Gravity Changes Raised by Dislocations in Spherically Symmetric Earth Models[D]. Tokyo: University of Tokyo, 1992
(  0) 0) |
| [16] |
Sun W K. Potential and Gravity Changes Caused by Dislocations in Spherically Symmetric Earth Models[J]. Bull Earthquake Res Inst, Univ Tokyo, 1992, 67: 89-238
(  0) 0) |
| [17] |
Sun W K, Okubo S. Surface Potential and Gravity Changes Due to Internal Dislocations in a Spherical Earth-Ⅰ. Theory for a Point Dislocation[J]. Geophys J Int, 1993, 114(3): 569-592 DOI:10.1111/gji.1993.114.issue-3
(  0) 0) |
| [18] |
Sun W K, Okubo S, Fu G Y. Green's Function of Co-Seismic Strain Changes and Investigation of Effects of Earth's Curvature and Radial Heterogeneity[J]. Geophys J Int, 2006, 167(3): 1 273-1 291 DOI:10.1111/gji.2006.167.issue-3
(  0) 0) |
| [19] |
Sun W K, Okubo S, Fu G Y, et al. General Formulations of Global Co-Seismic Deformations Caused by an Arbitrary Dislocation in a Spherically Symmetric Earth Model: Applicable to Deformed Earth Surface and Space-Fixed Point[J]. Geophys J Int, 2009, 177(3): 817-833 DOI:10.1111/gji.2009.177.issue-3
(  0) 0) |
| [20] |
Sun W K, Zhou X. Coseismic Deflection Change of the Vertical Caused by the 2011 Tohoku-Oki Earthquake (MW=9.0)[J]. Geophys J Int, 2012, 189(2): 937-955 DOI:10.1111/gji.2012.189.issue-2
(  0) 0) |
| [21] |
Okubo S. Reciprocity Theorem to Compute the Static Deformation Due to a Point Dislocation Buried in a Spherically Symmetric Earth[J]. Geophys J Int, 1993, 115(3): 921-928 DOI:10.1111/gji.1993.115.issue-3
(  0) 0) |
| [22] |
Pollitz F F. Coseismic Deformation from Earthquake Faulting on a Layered Spherical Earth[J]. Geophys J Int, 1996, 125(1): 1-14
(  0) 0) |
| [23] |
Wang R J, Lorenzo-Martín F, Roth F. Computation of Deformation Induced by Earthquakes in a Multi-Layered Elastic Crust-FORTRAN Programs EDGRN/EDCMP[J]. Computers and Geosciences, 2003, 29(2): 195-207
(  0) 0) |
| [24] |
郝金来, 姚振兴. 均匀弹性分层介质模型中的同震位移, 应变以及应力[J]. 地球物理学报, 2012, 55(5): 1 682-1 694 (Hao Jinlai, Yao Zhenxing. The Coseismic Displacement, Strain and Stress is the Layered Elastic Model[J]. Chinese J Geophys, 2012, 55(5): 1 682-1 694)
(  0) 0) |
| [25] |
Fu G Y, Sun W K. Surface Co-Seismic Gravity Changes Caused by Dislocations in a 3-D Heterogeneous Earth[J]. Geophys J Int, 2008, 172(2): 479-503 DOI:10.1111/gji.2008.172.issue-2
(  0) 0) |
| [26] |
Rundle J B. Viscoelastic-Gravitational Deformation by a Rectangular Thrust Fault in a Layered Earth[J]. J Geophys Res, 1982, 87(B9): 7 787-7 796 DOI:10.1029/JB087iB09p07787
(  0) 0) |
| [27] |
Pollitz F F. Postseismic Relaxation Theory on the Spherical Earth[J]. Bulletin of the Seismological Society of America, 1992, 82(1): 422-453
(  0) 0) |
| [28] |
Piersanti A, Spada G, Sabadini R, et al. Geobal Post-Seismic Deformation[J]. Geophys J Int, 1995, 120(3): 544-566 DOI:10.1111/j.1365-246X.1995.tb01838.x
(  0) 0) |
| [29] |
Sabadini R, Piersanti A, Spada G. Toroidal/Poloidal Partitioning of Global Post-Seismic Deformation[J]. Geophys Res Lett, 1995, 22(8): 985-988 DOI:10.1029/95GL00819
(  0) 0) |
| [30] |
Ma X Q, Kusznir N J. Effects of Rigidity Layering, Gravity and Stress Relaxation on 3-D Subsurface Fault Displacement Fields[J]. Geophys J Int, 1994, 118(1): 201-220 DOI:10.1111/gji.1994.118.issue-1
(  0) 0) |
| [31] |
Wang H S. Surface Vertical Displacements, Potential Perturbations and Gravity Changes of a Viscoelastic Earth Model Induced by Internal Point Dislocations[J]. Geophys J Int, 1999, 137(2): 429-440
(  0) 0) |
| [32] |
Tanaka Y, Okuno J, Okubo S. A New Method for the Computation of Global Viscoelastic Post-Seismic Deformation in a Realistic Earth Model (Ⅰ)-Vertical Displacement and Gravity Variation[J]. Geophys J Int, 2006, 164(2): 273-289 DOI:10.1111/gji.2006.164.issue-2
(  0) 0) |
| [33] |
Wang R J, Lorenzo-Martín F, Roth F. PSGRN/PSCMP—A New Code for Calculating Co-and Post-Seismic Deformation, Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J]. Computers & Geosciences, 2006, 32(4): 527-541
(  0) 0) |
| [34] |
Dong J, Sun W K, Zhou X, et al. An Analytical Approach to Estimate Curvature Effect of Coseismic Deformations[J]. Geophys J Int, 2016, 206(2): 1 327-1 339 DOI:10.1093/gji/ggw215
(  0) 0) |
| [35] |
孙文科. 地震位错理论[M]. 北京: 科学出版社, 2012 (Sun Wenke. Theory on Earthquake Dislocation[M]. Beijing: Science Press, 2012)
(  0) 0) |
2. Key Laboratory of Computational Geodynamics, CAS, A19 Yuquan Road, Beijing 100049, China
 2017, Vol. 37
2017, Vol. 37

