2. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079;
3. 国家测绘地理信息局第一大地测量队,西安市测绘路4号,710054
相比于卫星重力测量,航空重力测量空间分辨率更高,具备恢复重力场中短波信号的能力;相比于地面重力测量,航空重力测量具有高效率、低成本的优势,不受地面环境影响,在高山和荒漠地区也可以获取空间分布均匀的重力观测资料[1-3]。
GT-2A航空重力仪在GT-1A的基础上将测量动态范围由±500 Gal提高到了±1 000 Gal,能够适用于更复杂的测量环境。欧阳永忠等[4]的同机测试实验表明,相比于TAGS、WZ01和GDP-1三种型号的航空重力仪,GT-1A具有更好的综合性能技术指标。Wooldrigde[5]通过对重复测线的数据分析发现,GT-1A获取的2 km分辨率重力测量结果的精度优于1 mGal。之后他又通过对200 000 km航线上GT-1A重力观测值100 s滤波结果进行统计得出,由交叉点数据计算的测量精度为0.67 mGal,由重复测线数据计算的测量精度为0.70 mGal[6]。Olson [7]的研究表明,GT-2A与GT-1A的观测精度一致,且均优于AIR-Grav重力仪,在山谷地带进行的GT-1A和GT-2A同机测试实验中,有195个观测数据超出GT-1A的量程而无法记录,GT-2A却没有出现记录中断的情况。
2015年国家测绘地理信息局第一大地测量队采用引进的国内首台GT-2A航空重力仪在两个实验区实施了航空重力测量,同时在实验区地面布网,进行高精度的重力测量。本文基于两个实验区的航空重力和地面重力测量结果,评定GT-2A航空重力仪的内符合和外符合精度,为GT-2A航空重力仪在全国开展基础性航空重力测量业务提供技术指标的制定依据。
1 数据处理方法 1.1 航空重力数据归算航空重力数据归算包括将测线上的重力观测值归算到平均高程面上,然后进行测线网平差,并且格网化,具体方法见文献[8]。本文不同之处在于采用整体网平差法取代文献[8]中的两步平差法进行测线网平差,整体网平差法的具体实施见文献[9]。
主副测线交叉点不符值主要由传感器测量误差等低频误差引起[9]。本文假设这些误差为观测时间的线性函数,则第i条测线上第j个测点的观测误差可以表示为:
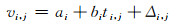
|
(1) |
式中,vi, j为观测误差,ti, j为由测线i第一个观测历元起算的第j个测点的观测时间,ai、bi为系统误差参数,Δi, j为随机误差。
假设第i条测线上的第j个测点与第k条测线上第p个测点重合形成交叉点,交叉点不符值li, jk, p可以表示为:
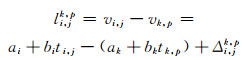
|
(2) |
写成矩阵形式为:
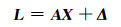
|
式中,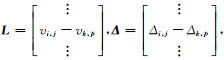
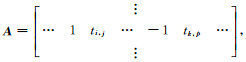
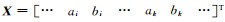
测线网平差属于秩亏网平差,本文采用L曲线法确定正则化参数α,依据最小二乘准则求解系统误差参数,即
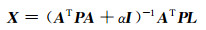
|
(3) |
式中,I为单位阵。
1.2 重力扰动延拓采用泊松积分法实现重力扰动延拓。对于球外的调和函数,可以利用泊松积分由球面上的函数值计算球外任意一点的函数值,即
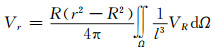
|
(4) |
式中,Vr和VR分别为球外和球面上的调和函数,R为球半径,r为球心与计算点的距离,l为球上面元dΩ到计算点的距离。
重力扰动是地球外部的调和函数,可以采用泊松积分实现重力扰动向上延拓。利用泊松积分将地面重力数据向上延拓到航空重力数据归算结果所在格网点上,实现航空重力与地面重力测量结果的比较。
另一种方法是将航空重力测量得到的空中重力扰动向下延拓到地面重力观测点上进行比较。本文采用泊松积分迭代法先将空中重力扰动延拓到大地水准面,再向上延拓到地面重力数据观测点处。泊松积分迭代法具体实施可参考文献[10-12]。
将空中重力扰动延拓到大地水准面上时,为了使重力扰动在大地水准面外满足泊松积分条件,需要先移除出大地水准面外的地形质量,计算得到地面重力扰动后,再恢复大地水准面外地形质量的影响。本文采用SRTM3地形模型和线质量模型[13]计算大地水准面外地形质量对重力扰动的影响:
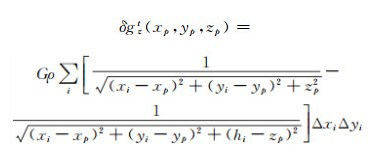
|
(5) |
式中,δgzt为地形对重力扰动的影响,G为引力常数,(xp, yp, zp)为计算点坐标。利用数字地形模型进行数值计算时,将地形划分为多个棱柱形质量块,xi、yi分别为质量块i的底面中心位置,ΔxiΔyi为质量块i的底面积,hi为地形模型中提取的质量块i的高程,ρ取地壳平均密度2.67 g/cm3。
另外,在利用泊松积分向上延拓时,将积分区域划分为近区和远区,近区贡献可以采用重力观测资料进行数值积分计算,远区贡献则采用重力位模型计算。泊松积分的远区贡献计算公式为:
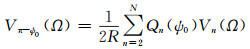
|
(6) |
式中,V为调和函数,Vn(Ω)为计算点Ω处V的第n阶分量,V代表重力扰动时,可以由重力位模型计算Vn(Ω);N为截断阶数,其选取可参考文献[14];Qn(ψ0)为泊松截断系数,ψ0为近区半径。Qn(ψ0)的逼近公式为[15]:
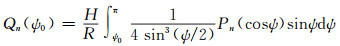
|
(7) |
式中,H为延拓高度,Pn(cos)为勒让德多项式。
2 精度评定 2.1 实验数据说明采用A、B两个测区的航空重力实测数据和对应的地面重力观测数据对GT-2A的精度进行评定。A区属于荒漠地区,地形起伏平缓;B区为山地,地形起伏较大。表 1为测区内SRTM3数据的统计结果(单位m)。
|
|
表 1 测区SRTM3数据统计结果 Tab. 1 Statistical results of SRTM3 data |
空中作业范围约为1°×0.5°,东西向测线与南北向测线交叉,飞行速度约为80 m/s,数据处理中空中重力扰动结果经过100 s低通滤波,相邻测线间隔约5 km,即空中重力扰动的空间分辨率为4~5 km。同时采用相对重力仪采集测区内的地面重力数据,在A区布设间隔为5 km的规则重力观测网点;B区受到地形限制,地面重力观测点沿公路布设,分布不均匀。两个测区在实施地面重力测量时都进行了二等重力联测,结果表明,地面重力观测结果的精度优于0.07 mGal,远高于航空重力测量的精度。空中和地面重力数据的空间分布见1,图中灰色线为飞机航线,即空中测量结果的分布情况,黑色圆点为地面重力观测点。
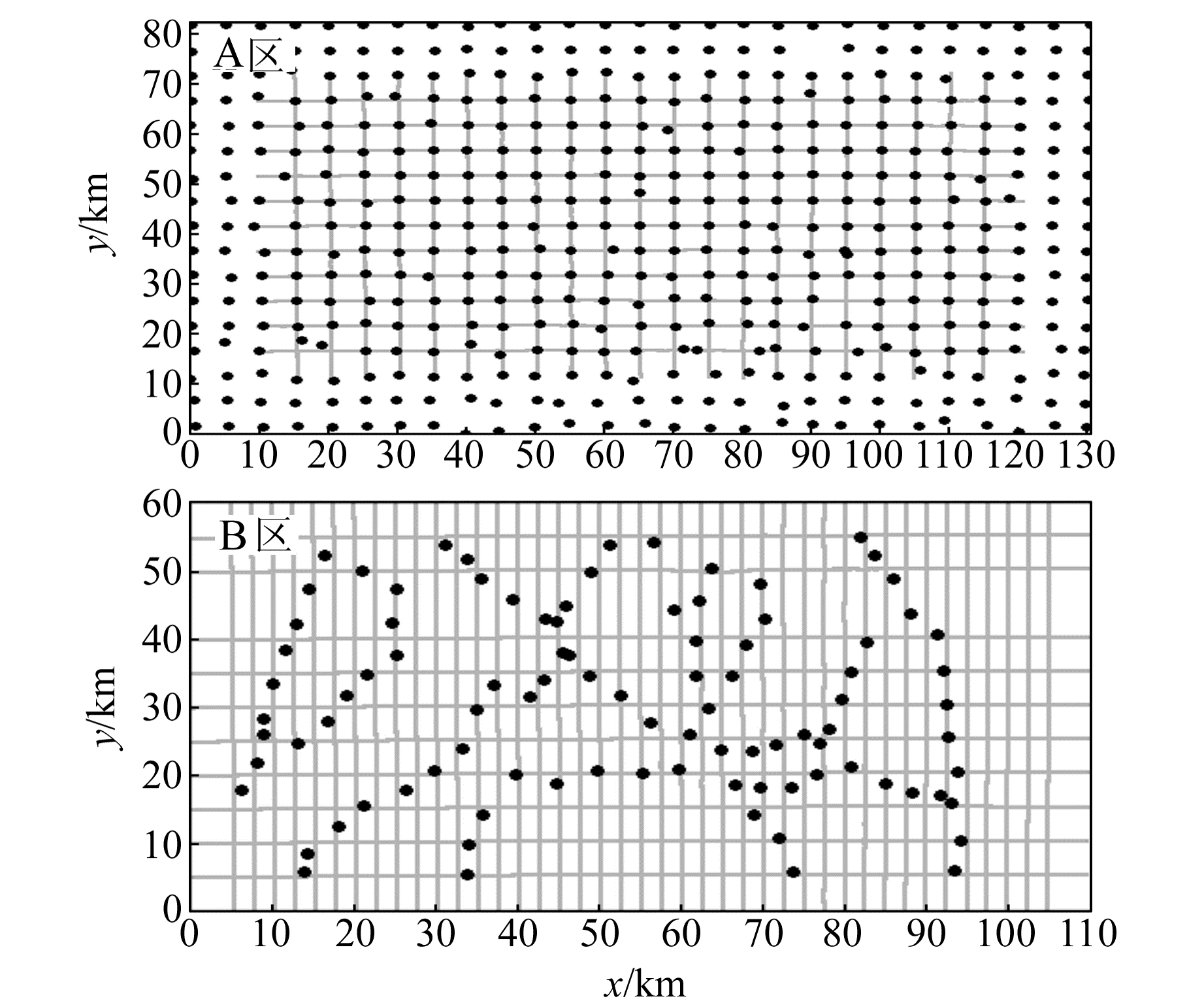
|
图 1 空中和地面重力观测数据空间分布 Fig. 1 The spatial distribution of airborne and ground gravity data |
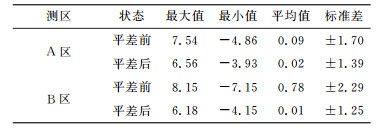
采用南北向与东西向测线交叉点处的重力扰动观测结果评定GT-2A的内符合精度。分别计算测线网平差前与平差后的交叉点不符值,其分布见图 2和图 3,统计结果见表 2(单位mGal)。
|
|
表 2 交叉点不符值统计结果 Tab. 2 Statistical results of the discrepancies on cross points |

|
图 2 测线网平差前交叉点不符值 Fig. 2 The discrepancies on cross points before crossover adjustment |
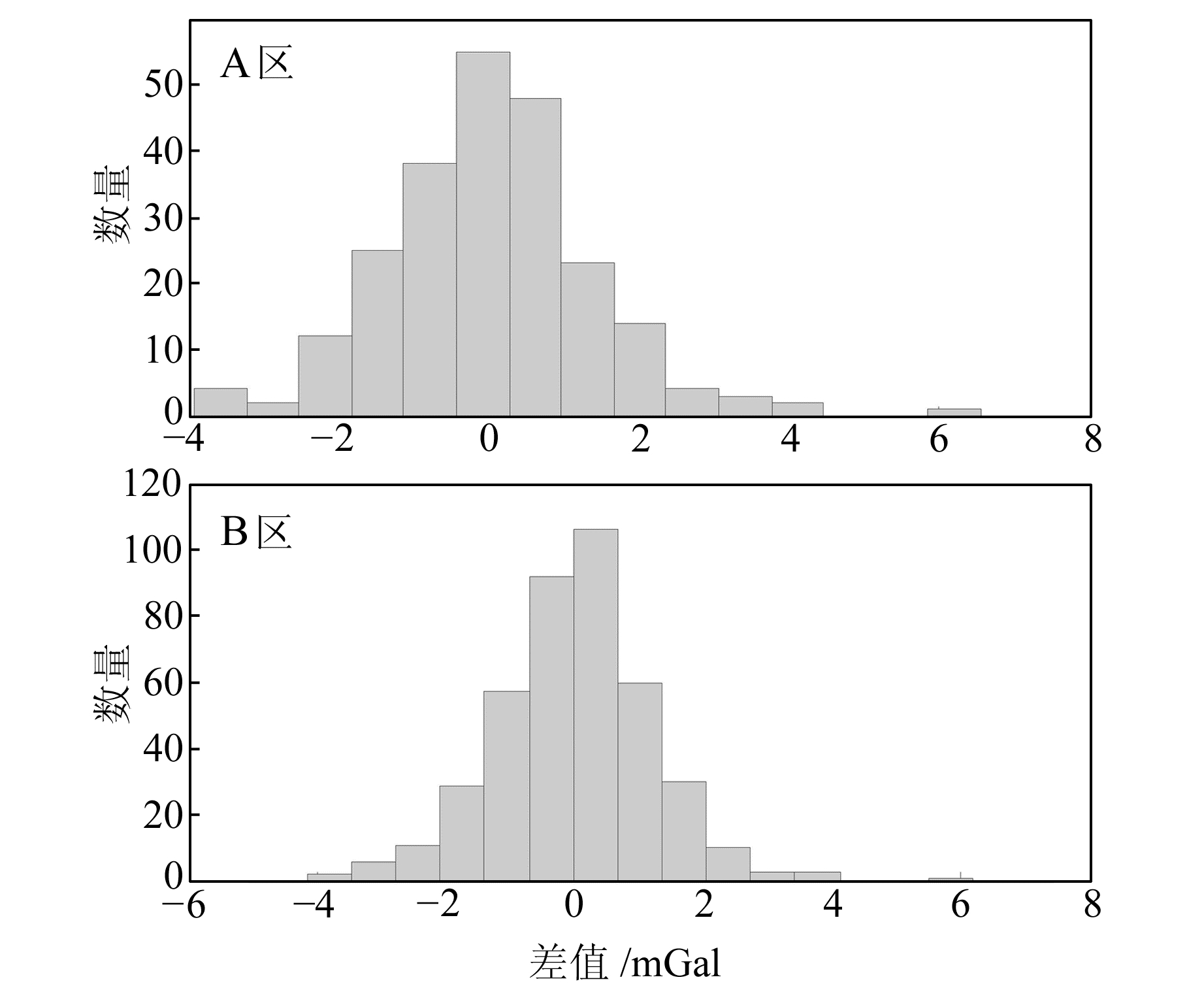
|
图 3 测线网平差后交叉点不符值 Fig. 3 The discrepancies on cross points after crossover adjustment |
从表 2可以看出,平差前A区交叉点不符值的标准差为±1.70 mGal,B区交叉点不符值的标准差为±2.29 mGal;平差后A区交叉点不符值的标准差为±1.39 mGal,B区交叉点不符值的标准差为±1.25 mGal。根据误差传播定律,将交叉点不符值标准差的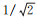
从图 3可知,平差后B区交叉点不符值更接近于正态分布。B区交叉点数量为410个,A区交叉点数量为331个,B区交叉点更多,统计结果更接近于真实精度。而A区由于交叉点较少,统计结果容易受到个别较大不符值的影响,这可能是导致A区交叉点统计精度比B区略低的原因。总体而言,GT-2A航空重力仪的内符合精度优于1.0 mGal。
2.3 外符合精度采用精度较高的地面重力数据评定GT-2A的外符合精度,主要工作在于将两类数据延拓到相同的位置进行比较。对于A区,由于地面重力数据分布均匀且超出空中作业范围,可以将地面重力扰动延拓到空中数据归算后所在格网点上进行比较,也可以将空中重力扰动延拓到地面重力观测点上进行比较;对于B区,由于地面重力数据较少且分布不均匀,只能将空中重力扰动延拓到地面重力观测点上进行比较。在延拓过程中,为了减弱边缘效应的影响,采用EGM08重力场模型填充重力扰动数据,使得原有测区向外扩展30′。
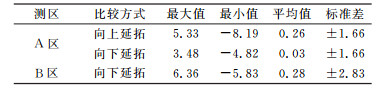
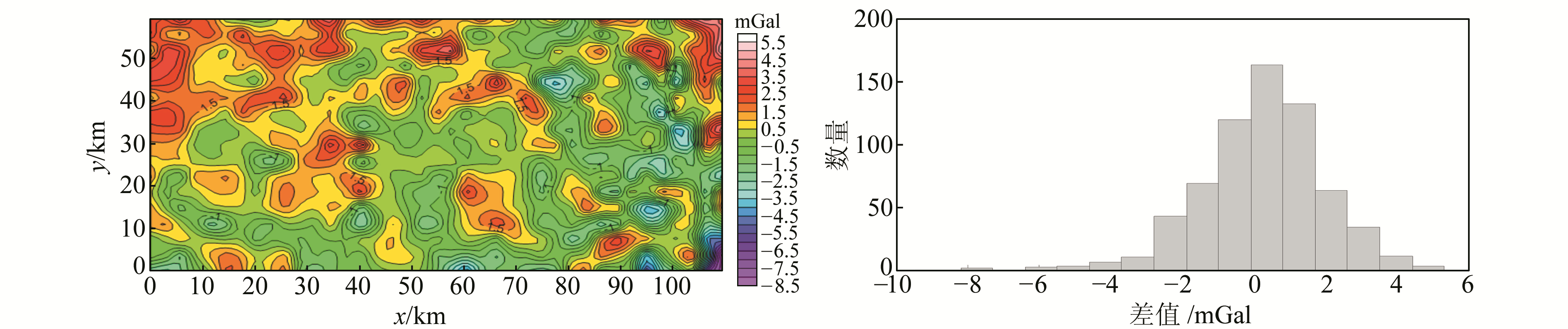
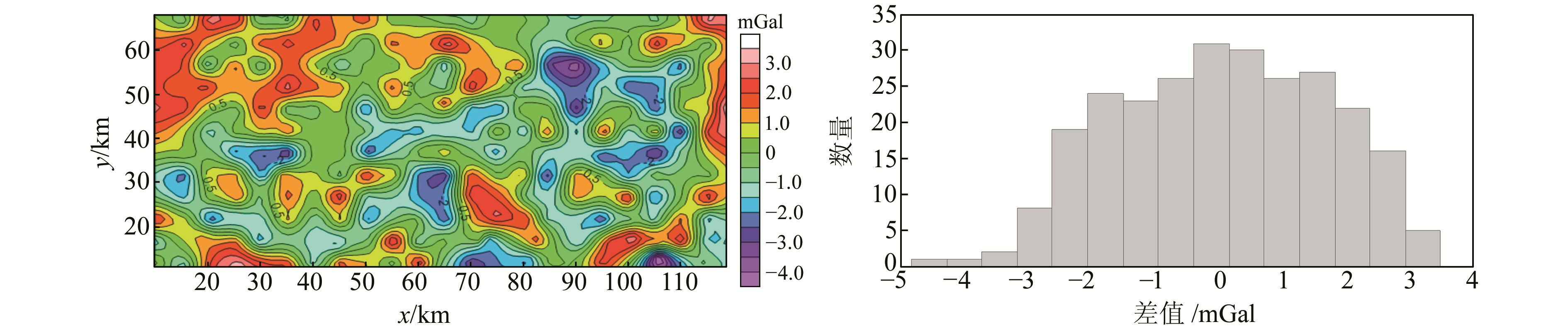
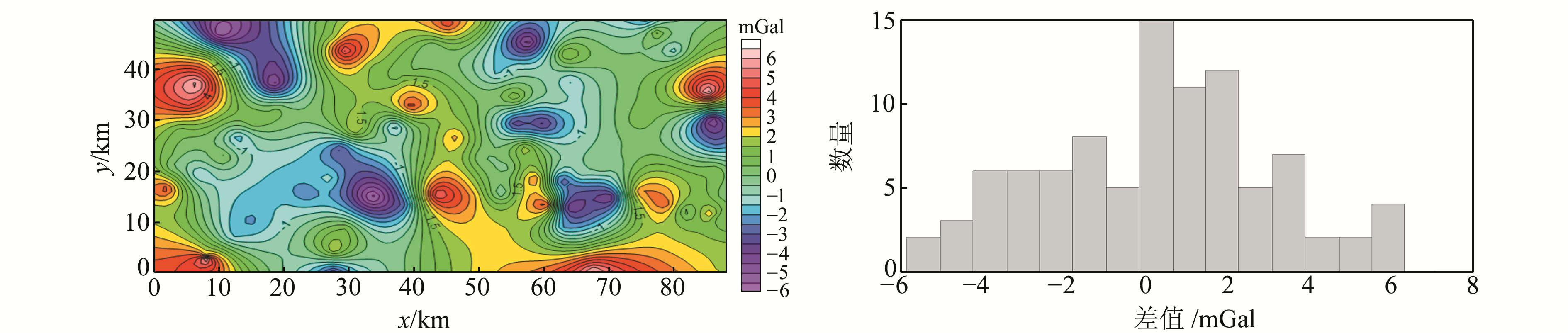
A区地面重力扰动数据向上延拓到空中格网点,与空中重力扰动观测结果的差值见图 4。A区和B区的空中重力扰动数据分别向下延拓到地面,与地面重力扰动观测结果的差值分别见图 5和图 6。表 3给出了3项比对实验的差值统计结果(单位mGal)。
|
图 4 A区向上延拓比对结果 Fig. 4 The differences between upward results of ground gravity and airborne gravity in zone A |
|
图 5 A区向下延拓比对结果 Fig. 5 The diffrences between downward results of airborne gravity and gound gravity in zone A |
|
图 6 B区向下延拓比对结果 Fig. 6 The diffrences between downward results of airborne gravity and gound gravity in zone B |
|
|
表 3 空中与地面重力扰动观测结果比对 Tab. 3 Comparison of airborne and ground gravity data after continuation |
表 3的统计结果表明,无论是采用向上延拓还是向下延拓的方式进行比较,A区差值标准差均为±1.66 mGal;B区采用向下延拓的方式进行比较,差值标准差为±2.83 mGal。由于地面重力测量结果的精度远远高于航空重力测量,所以在不考虑格网化和延拓等数据处理过程引入的误差时,此处的差值标准差可以直接代表航空重力测量获取的空中重力扰动的外符合精度。
3 结语GT-2A航空重力测量结果在A、B测区的内符合精度一致,均优于1 mGal。用地面重力观测结果评定的外符合精度存在差异,在A区为1.66 mGal,在B区为2.83 mGal。前者表明航空重力观测结果几乎不受地形的影响,后者表明空中重力扰动向下延拓结果受地形影响较大。在地形起伏较大的山区,空中重力扰动向下延拓结果的精度偏低,可能的原因有:1)山区施测时飞行高度和速度较大,造成延拓高度大,而向下延拓是一个高频噪声放大过程,致使延拓结果的精度较低,数据分辨率也会降低;2)山区SRTM3地形模型和EGM08模型的误差较大,该误差会引入到向下延拓结果中。后续研究需要改进向下延拓方法,有望进一步提高航空重力向下延拓结果的精度。
| [1] |
王丽红.航空重力测量中载体矢量加速度的确定方法[D].郑州: 信息工程大学, 2008 (Wang Lihong. Determination of Vector Acceleration for Airborne Vector Gravimetry[D]. Zhengzhou: Information Engineering University, 2008)
(  0) 0) |
| [2] |
王静波.航空重力测量数据处理方法技术研究[D].北京: 中国地质大学(北京), 2010 (Wang Jingbo. Methodologies and Technology of Data Processing for Airborne Gravimetry[D]. Beijing: China University of Geosciences, 2010)
(  0) 0) |
| [3] |
Mueller F, Mayer-Guerr T. Comparison of Downward Continuation Methods of Airborne Gravimetry Data[A]//A Window on the Future of Feodesy[M].Berlin Heidelberg: Springer, 2005
(  0) 0) |
| [4] |
欧阳永忠, 邓凯亮, 陆秀平, 等. 多型航空重力仪同机测试及其数据分析[J]. 海洋测绘, 2013, 33(4): 6-11 (Ouyang Yongzhong, Deng Kailiang, Lu Xiuping, et al. Tests of Multi-type Airborne Gravimeters and Data Analysis[J]. Hydrographic Surveying and Charting, 2013, 33(4): 6-11 DOI:10.3969/j.issn.1671-3044.2013.04.002)
(  0) 0) |
| [5] |
Wooldridge A. GT-1A Airborne Gravity: A Case History over the Vredefort Dome, South Africa[C]. ASEG Airborne Gravity Workshop, Sydney, 2004
(  0) 0) |
| [6] |
Wooldridge A. Review of Modern Airborne Gravity Focusing on Results from GT-1A Surveys[J]. First Break, 2010, 28(5): 85-92
(  0) 0) |
| [7] |
Olson D. GT-1A and GT-2A Airborne Gravimeters: Improvements in Design, Operation and Processing from 2003 to 2010[C]. ASEG-PESA Airborne Gravity 2010 Workshop, Sydney, 2010
(  0) 0) |
| [8] |
周波阳, 罗志才, 钟波, 等. 航空重力测量的数据归算方法[J]. 大地测量与地球动力学, 2015, 35(2): 336-341 (Zhou Boyang, Luo Zhicai, Zhong Bo, et al. Data Reduction Methods of Airborne Gravimetry[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 336-341)
(  0) 0) |
| [9] |
蔡劭琨.航空重力测量网络平差方法研究[D].长沙: 国防科学技术大学, 2009 (Cai Shaokun. Research on the Network Adjustment of Airborne Gravimetry[D]. Changsha: National University of Defense Technology, 2009)
(  0) 0) |
| [10] |
卢雪盈, 柳林涛, 梁星辉, 等. 航空重力数据向下延拓的逆泊松积分算法[J]. 大地测量与地球动力学, 2015, 35(6): 919-922 (Lu Xueying, Liu Lintao, Liang Xinghui, et al. The Inverse Possion Integral Algorithm for Downward Continuation of Airborne Gravity Data[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 919-922)
(  0) 0) |
| [11] |
周波阳, 罗志才, 许闯, 等. 航空重力数据向下延拓的FFT快速算法比较[J]. 大地测量与地球动力学, 2013, 33(1): 64-73 (Zhou Boyang, Luo Zhicai, Xu Chuang, et al. Comparison among Fast Fourier Transform Algorithms for Downward Continuation of Airborne Gravity Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 64-73)
(  0) 0) |
| [12] |
徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报, 2007, 50(1): 285-289 (Xu Shizhe. A Comparison of Effects between the Iteration Method and FFT for Downward Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2007, 50(1): 285-289 DOI:10.3321/j.issn:0001-5733.2007.01.035)
(  0) 0) |
| [13] |
罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报:信息科学版, 2003, 28(3): 340-344 (Luo Zhicai, Chen Yongqi, Ning Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3): 340-344)
(  0) 0) |
| [14] |
欧阳永忠, 邓凯亮, 黄谟涛, 等. 重力异常延拓积分半径的选择及远区效应[J]. 海洋测绘, 2011, 31(4): 5-12 (Ouyang Yongzhong, Deng Kailiang, Huang Motao, et al. The Choice of Integral Radius and Its Far-Zone Effects in the Continuation of the Gravity Anomaly[J]. Hydrographic Surveying and Charting, 2011, 31(4): 5-12 DOI:10.3969/j.issn.1671-3044.2011.04.002)
(  0) 0) |
| [15] |
Martinec Z. Stability Investigation of a Discrete Downward Continuation Problem for Geoid Determination in the Canada Rocky Mountains[J]. Journal of Geodesy, 1996, 70(11): 805-828 DOI:10.1007/BF00867158
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. The Geodetic First Team of NASMG, 4 Cehui Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37