2. 湖南省精密工程测量与形变灾害监测重点实验室,长沙市麓山南路932号,410083
随着大量连续运行卫星定位服务综合系统的建成,高精度、高时空分辨率的ZTD数据的获取变得简单。直接利用该ZTD数据可建立无需气象参数输入的对流层延迟改正模型[1]。按覆盖范围,可以将现有ZTD模型分为两种:一种是区域模型,如戴吾蛟等[2]建立的香港区域精密对流层模型;另一种是全球模型,如姚宜斌等[3]建立的GZTD全球模型。其中,前者的区域模型需要选择一个站点作为基准,而对于范围较大的区域,选择一个合适的基准较为困难;后者的全球模型建模方法比较复杂,且所需参数较多。本文提出一种基于PCA的ZTD时空建模方法,该方法模型参数较少且建模迅速。
1 PCA进行ZTD时空建模理论方法PCA是一种多变量分析技术,其通过一种变换,将观测到的混合多维数据中包含的主要信息由较少的主成分分量表示。PCA处理的具体步骤参见文献[4]。
1.1 PCA时空建模方法PCA时空建模的基本思想是[5-6]:首先认为在空间上不同站点观测得到的时间数据序列是由少数几种不同影响因素在该点共同作用的结果,这些影响因素即主成分分析时所选取的主成分分量,而各因素在该点作用的大小即该因素对应的空间响应值大小,称为特征向量;根据PCA基本原理,每个站点的ZTD时间序列即为观测得到的混合信号,通过主成分分析时所选取的主成分分量与其所对应的特征向量的乘积之和,即可较好地恢复出原始的混合信号;基于此,对所有测站数据序列进行PCA处理,可得到比站点观测序列个数少很多的主成分分量及对应的特征向量;分别对各主成分分量进行时间序列建模,对各特征向量进行空间建模,再由二者相乘累加即可建立相应的时空模型。
由于PCA处理时,要求其输入信号为平稳序列[7-8],故建模时需对各站点观测数据序列进行去均值化处理。利用PCA进行ZTD时空建模的基本过程如下:
1) 选择某一区域内各站点观测数据序列,计算各站点的年均值avg;
2) 对原始数据进行去均值处理,计算数据去均值后的协方差矩阵R的前m个大的主成分分量及其对应的特征向量,根据各主成分的贡献率、累积贡献率和主成分得分,选取合适数量的主成分分量PCs并得到其对应的特征向量Vs;
3) 分别对年均值avg和各特征向量V进行空间建模;
4) 对各主成分分量PC进行时间趋势建模;
5) 把模型计算的年均值项与各主成分分量与其特征向量的乘积项相加,得到ZTD时空模型。
1.2 ZTD时空建模应用ZTD数据序列是典型的时空数据序列,且具有明显的年周期性[9]。下面详细介绍区域对流层延迟时空模型的建立过程。
1) 建立ZTD年均值模型。若建模区域范围较小或气象条件比较稳定(如香港地区),则将纬度B(rad)按式(1)转化成两倍余弦函数值,再将其和高程h作为参数,对ZTD年均值进行曲面拟合,拟合公式如式(2)所示:
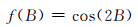
|
(1) |
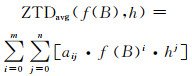
|
(2) |
式中,B为纬度,ZTDavg为ZTD年均值,h为高程(m),[aij]为m×n的系数矩阵。
若建模区域范围较大(如中国地区)或气象条件多变(如云南地区),则采用克里金插值法建立年均值模型。以取整后的检查点经纬度为中心,划定一个5°×5°的正方形移动格网;根据落在移动格网内的各站点与待插值站点的位置(纬度B和高程h)关系及其观测值大小,给其赋予一定的权重;最后进行滑动加权平均。计算公式为:

|
(3) |
式中,ZTDavg为待插值站点的ZTD年均值,n为落在移动格网内的站点数量,λi为第i个测站ZTD年均值的权重,Z(Xi)为第i个测站的ZTD年均值。
2) 建立主成分分量模型。对去除年均值后的ZTD数据进行PCA处理,根据信息提取效果选取合适数量(香港地区3个、云南地区5个、中国地区12个)的主成分分量,并以年积日(doy)为参数,对各主成分分量进行建模。采用傅里叶曲线拟合,模型公式为:
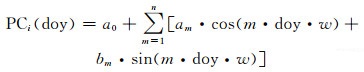
|
(4) |
式中,PCi为第i个主成分分量,doy为年积日,a0为常数项,n为展开级数(根据实际拟合精度确定),am、bm(m=1, 2…, n)为系数项,w为傅里叶展开的频率变量。
3) 建立特征向量模型。先将经度L(rad)、纬度B(rad)按式(5)转换成余弦函数值,对特征向量进行相关性分析,在其中选择相关性较强的一个与高程h作为参数,对特征向量进行建模。模型公式如式(6)所示:

|
(5) |
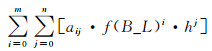
|
(6) |
式中,L(rad)为经度,B(rad)为纬度,Vi为第i个主成分分量对应的特征向量,f(B_L)为经度L和纬度B的两倍余弦值中相关性较大的一个,h为高程(m),[aij]为m×n的系数矩阵,m、n的大小根据实际拟合精度而定。
4) 得到区域时空模型。结合以上结果,得到最终的区域对流层延迟时空模型为:
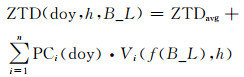
|
(7) |
3个模型建立后,利用参与建模的数据对模型进行内符合精度检验,利用未参与建模的数据对模型进行外符合精度检验,并将新模型与其他已有的模型(Saastamoinen模型,EGNOS模型、UNB3m模型)进行对比。其中,在香港地区,Saastamoinen模型采用香港天文台发布的气象参数;在云南地区和中国地区,采用加拿大纽布伦斯威克大学开发的DIPOP软件[10]计算得到。
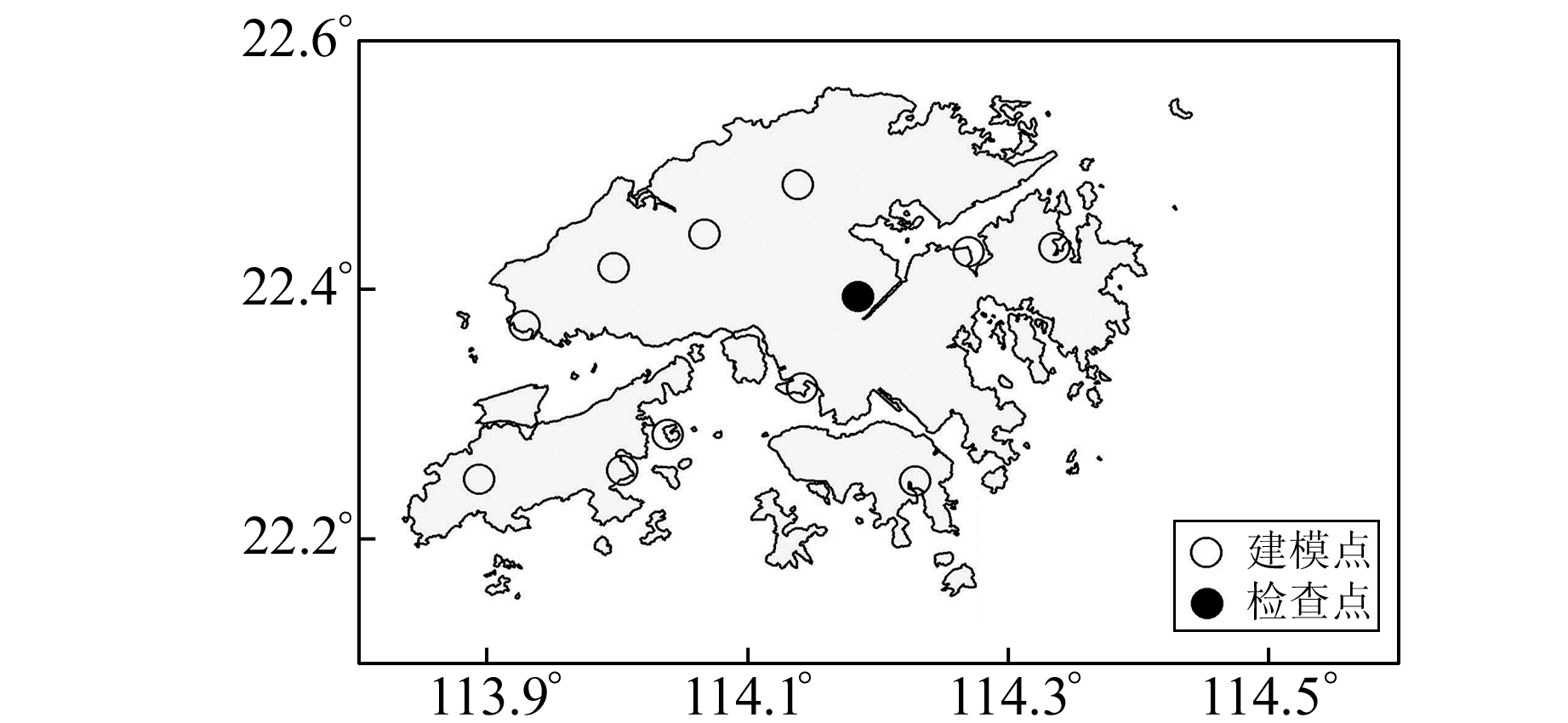
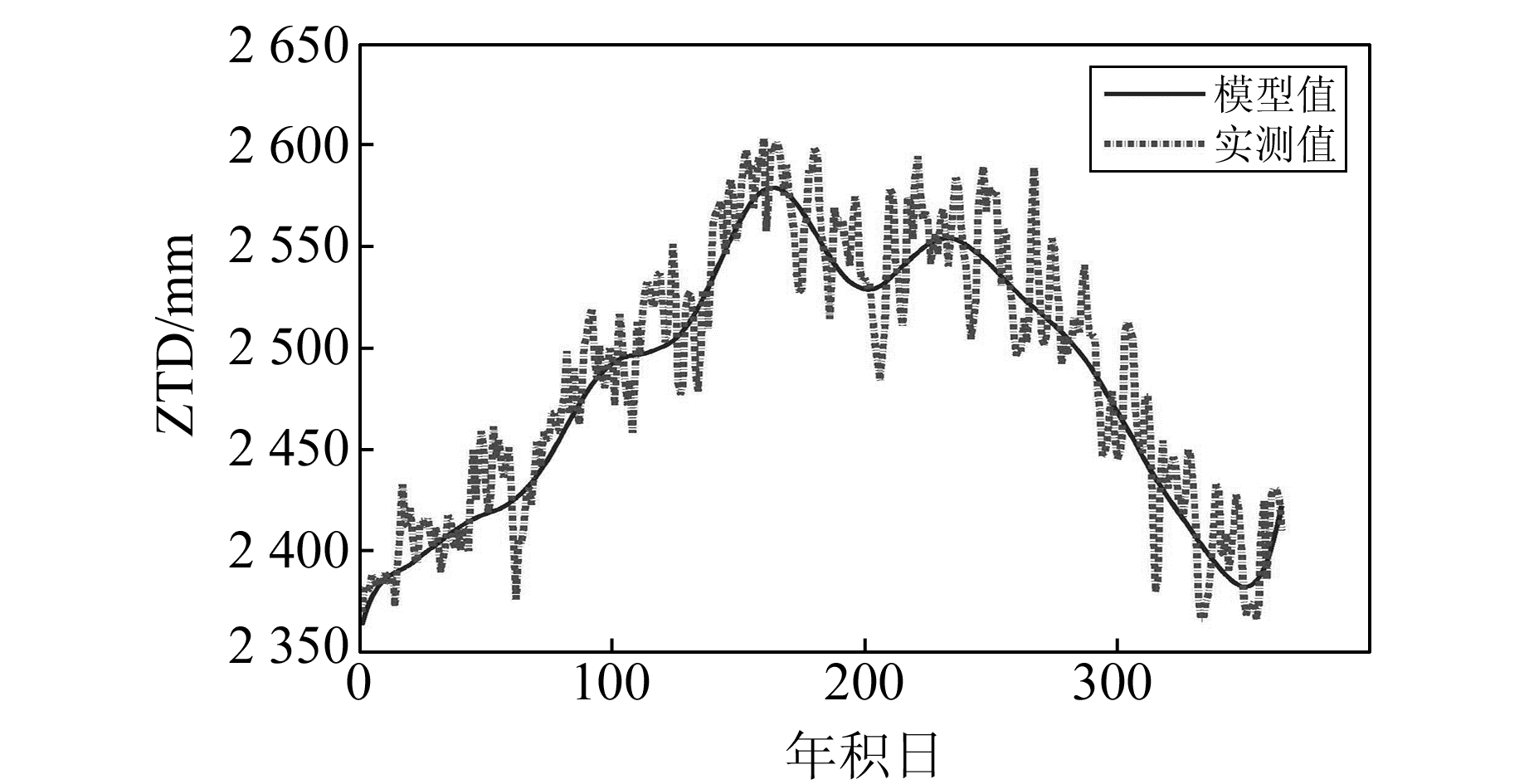
2.1 香港地区选择香港地区CORS网2005~2007年的ZTD观测数据的平均值作为1 a的ZTD时间序列进行处理,时间分辨率为1 d。其中,HKST测站作为检核站点,其他测站作为建模站点,具体点位空间分布情况如图 1所示。图 2为HKST测站新模型计算值和实测值的对比图,表 1(单位mm)为各模型计算值与实测值之差的RMS值。
|
图 1 香港地区所选站点空间分布 Fig. 1 Spatial distribution of selected sites in Hong Kong |
|
图 2 HKST检查点的检核效果 Fig. 2 Check effect of HKST site |
|
|
表 1 不同模型HKST检查点的RMS值 Tab. 1 Comparison of RMS values of different models in HKST site |
从检核效果图中可以看出,对于HKST测站,模型的计算结果与真值吻合良好,模型曲线走势与实测数据高度一致。从表 1可以看出,新模型的RMS值约为Saastamoinen模型的1/2、EGNOS和UNB3m模型的1/3,说明香港地区ZTD时空模型的对流层延迟改正精度降低了RMS值,精度明显高于Saastamoinen、EGNOS和UNB3m模型。为检验新模型在时间上的可靠性,将2008年HKST测站的ZTD观测值与模型计算值进行检验,其误差RMS值为36.6 mm,与建模时段的RMS值差别不大,说明模型在时间上有较好的预报精度,这也验证了根据ZTD年变化周期对其进行时空建模的可行性[2-3]。
2.2 云南地区选择中国大陆构造环境监测网络发布的云南地区30个CORS站点2015年的ZTD观测数据进行处理,将时间分辨率为1 h的ZTD值取日均值,得到时间分辨率为1 d的ZTD时间序列,其中27个站点用于建模,3个站点进行检核,其点位空间分布如图 3所示。图 4为YNTH检核站新模型计算值和实测值的对比图,表 2(单位mm)为各模型计算值与实测值之差的RMS值。

|
图 3 云南地区所选站点空间分布 Fig. 3 Spatial distribution of selected sites in Yunnan |
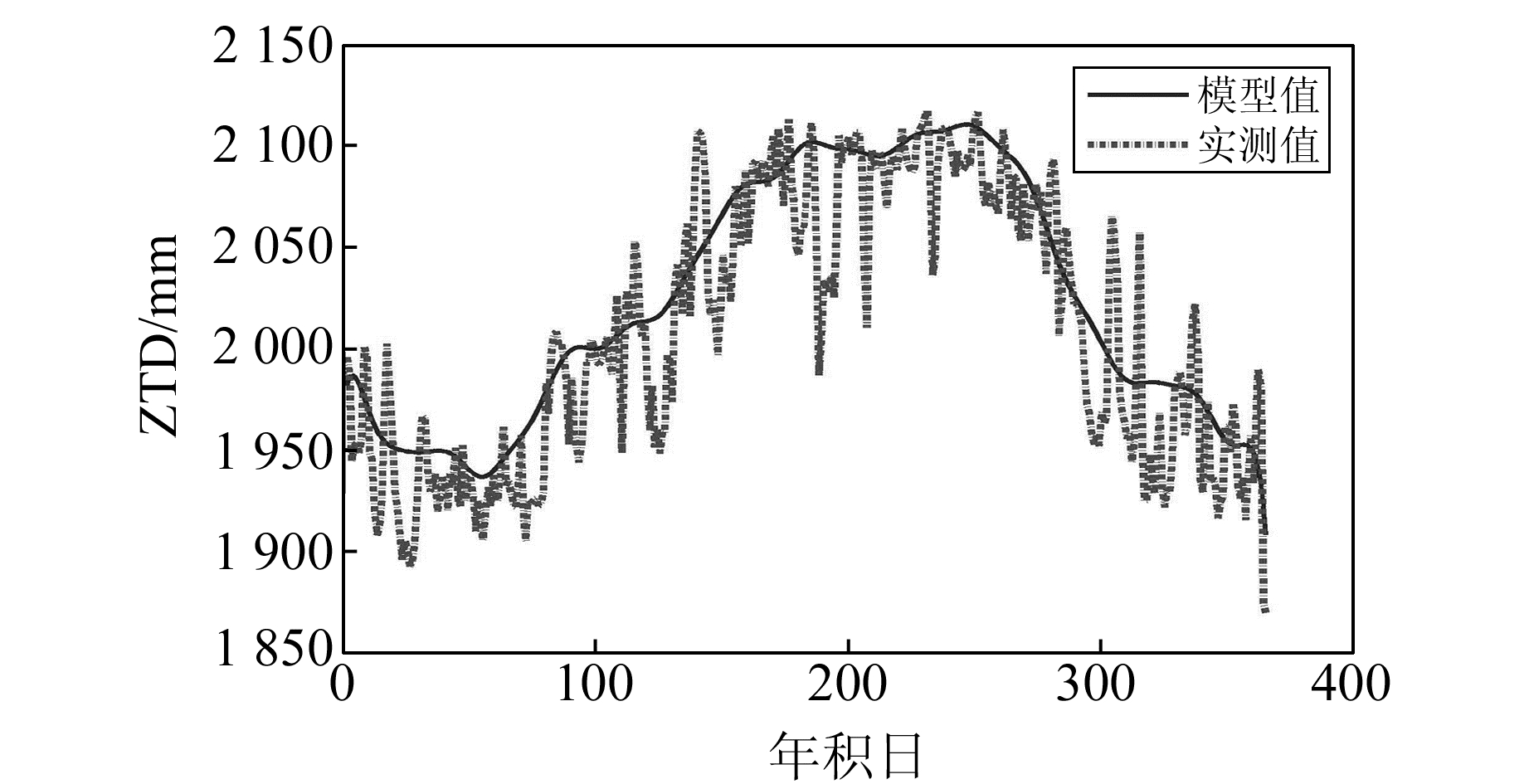
|
图 4 YNTH检核点的检核效果 Fig. 4 Check effect of YNTH site |
|
|
表 2 不同模型3个检核点的RMS值 Tab. 2 Comparison of RMS values of different models in three sites |
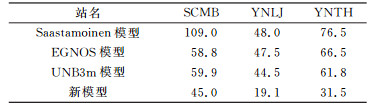
从检核效果图中可以看出,在YNTH检核点上模型的计算结果与真值吻合较好。从表 2可以看出,3个检核点中,新模型的RMS值约为Saastamoinen模型的1/2,除SCMB点外,约为EGNOS和UNB3m模型的1/2;在SCMB点上,新模型的RMS值比EGNOS和UNB3m模型小15 mm左右,说明云南地区ZTD时空模型的改正精度明显高于Saastamoinen、EGNOS和UNB3m模型。受实验数据的限制,只选择了2012年YNTH测站的ZTD观测值来检验新模型在时间上的可靠性,其RMS值为41.5 mm,与建模时段该测站的RMS值差别不大,说明模型在时间上有较高的预报精度,符合时空模型的特征。
2.3 中国地区选择中国大陆构造环境监测网络发布的中国地区163个CORS站点2015年的ZTD观测数据进行处理,将时间分辨率为1 h的ZTD值取日均值,得到时间分辨率为1 d的ZTD时间序列,其中159个站点用于建模,4个站点进行检核,其点位空间分布如图 5所示。为检验新模型在时间上的可靠性,将2012年GSLZ、KMIN、SCDF、TASH测站的ZTD观测值与模型计算值进行检验。图 6为JIXN检核站新模型计算值和实测值的对比图,表 3(单位mm)为2015年各模型计算值与实测值之差的RMS值,表 4(单位mm)为2012年新模型计算值与实测值之差的RMS值。

|
图 5 中国地区所选站点空间分布 Fig. 5 Spatial distribution of selected sites in China mainland |

|
图 6 JIXN检核点的检核效果 Fig. 6 Check effect of JIXN site |
|
|
表 3 不同模型4个检核点的RMS值 Tab. 3 Comparison of RMS values of different models in four sites |
|
|
表 4 2012年4个检核点RMS值统计 Tab. 4 RMS values of four sites in 2012 |
从检核效果图中可以看出,在JIXN检核点上模型的计算结果与真值吻合良好,但是对于一些变化较快的ZTD值,如年积日200附近,新模型计算值与真值存在较大的差别。出现这种情况可能是由于实验过程中没有考虑极端天气条件的影响,因为此时正值我国旱涝发生最频繁的7月[11],对流层中的水汽含量变化比较迅速。从表 3中可以看出,4个检核点中,除GSJT点外,新模型的RMS值约为Saastamoinen模型的1/2;在JIXN点和YNYA点上,新模型的RMS值小于EGNOS和UNB3m模型;而在GSJT点和XJDS点上,新模型的RMS值大于EGNOS和UNB3m模型。从表 4中可以看出,2012年4个检核点的误差RMS值均比较小,而且数值很稳定,说明新模型能在时间上较好地进行预报,稳定性强。
为了找到新模型在个别检核点上RMS值偏大的原因,本文通过代入测站点天顶对流层延迟真实年均值进行检验,结果如表 3所示。可以看出,GSJT点和XJDS点的RMS值得到了显著降低,模型改正效果大大改善。该结果表明,在个别检查点上,新模型改正效果较差可能是由于该站点的年均值插值误差较大。由于实验所收集的数据有限,在采用5°×5°的正方形移动格网进行克里金插值计算站点ZTD年均值时,无法保证格网内站点的数量足够均匀,所以在个别站点上,克里金插值计算年均值的误差较大,这直接导致所建模型的改正效果不佳。如果能获取足够密度站点的ZTD观测数据,那么克里金插值计算年均值的精度应该会有较大的提高,模型的精度也会得到相应的改善。
3 结语本文研究结果表明,利用PCA方法可建立精度更高、使用更简便、无需输入气象参数的ZTD时空模型。若能获得空间分辨率更高的GNSS站点长期稳定的观测数据,利用PCA建立的区域ZTD时空模型的精度将进一步提高。但对一些特殊的天气情况,模型的误差仍较大,今后建模时可以考虑增加特殊气象条件因素。当建模区域范围较大时,建立高精度ZTD年均值模型和特征向量模型是ZTD时空建模的关键,如何利用PCA方法建立更大范围的ZTD时空模型还有待进一步研究。
| [1] |
赵岩.区域对流层延迟建模分析[D].长沙: 中南大学, 2013 (Zhao Yan. Modeling and Analysis of Regional Tropospheric Delay[D]. Changsha: Central South University, 2013)
(  0) 0) |
| [2] |
戴吾蛟, 陈招华, 匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报:信息科学版, 2011, 36(4): 392-396 (Dai Wujiao, Chen Zhaohua, Kuang Cuilin, et al. Modeling Regional Precise Tropospheric Delay[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 392-396)
(  0) 0) |
| [3] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227)
(  0) 0) |
| [4] |
王学民. 应用多元分析[M]. 上海: 上海财经大学出版社, 2004 (Wang Xuemin. Application of Multivariate Analysis[M]. Shanghai: Shanghai University of Finance and Economics Press, 2004)
(  0) 0) |
| [5] |
Dai W J, Liu B, Meng X L, et al. Spatio-Temporal Modelling of Dam Deformation Using Independent Component Analysis[J]. Survey Review, 2014, 46(339): 437-443 DOI:10.1179/1752270614Y.0000000112
(  0) 0) |
| [6] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research Atmospheres, 2006, 111(B3): 1581-1600
(  0) 0) |
| [7] |
孟生旺. 用主成分分析方法进行多指标综合评价应注意的问题[J]. 统计研究, 1992, 9(4): 67-68 (Meng Shengwang. Using Principal Component Analysis Method to Evaluate the Problem of Multi Index Comprehensive Evaluation[J]. Statistical Research, 1992, 9(4): 67-68)
(  0) 0) |
| [8] |
纪荣芳. 主成分分析法中数据处理方法的改进[J]. 山东科技大学学报, 2007, 26(5): 95-98 (Ji Rongfang. Improvement of Data Processing Method in Principal Component Analysis[J]. Journal of Shandong University of Science and Technology, 2007, 26(5): 95-98 DOI:10.3969/j.issn.1672-3767.2007.05.023)
(  0) 0) |
| [9] |
Li W, Yuan Y B, Ou J K, et al. New Versions of the BDS/GNSS Zenith Tropospheric Delay Model IGGtrop[J]. Journal of Geodesy, 2015, 89(1): 73-80 DOI:10.1007/s00190-014-0761-5
(  0) 0) |
| [10] |
Vaníĉek P, Beutler G, Kleusberg A, et al. DIPOP-Differential Positioning Program Package for the Global Positioning System[J]. Progress in Astronautics & Aeronautics, 1985, 35(2): 197-216
(  0) 0) |
| [11] |
熊敏诠, 陈菊英. 中国7月降水分型及其成因[J]. 气象, 2001, 27(6): 43-46 (Xiong Minquan, Chen Juying. Precipitation Distribution Pattern of China in July and Its Cause[J]. Meteorological Monthly, 2001, 27(6): 43-46)
(  0) 0) |
2. Key Laboratory of Precise Engineering Surveying & Deformation Disaster Monitoring of Hunan Province, 932 South-Lushan Road, Changsha 410083, China
 2017, Vol. 37
2017, Vol. 37