基于BDS的时间传递是BDS应用研究的热点问题之一。在BDS精密星历和精密钟差产品发布之前,已有不少学者采用北斗共视法(BDS common view,BDS CV)进行基于BDS的时间传递研究,时间传递精度能达到ns级[1-2]。但BDS CV法缺点明显,如只适用于长度较短的对比链路,一旦链路长度过大,就需要在链路中间选择中继站,否则无法保障链路两端共视同一颗卫星。但增设中继站的做法会带来另一个弊端——链路两端电离层、对流层误差相关性大大降低,同源误差消除效果变差[3]。目前基于GPS的高精度时间传递通常采用载波相位法,时间传递精度通常可以达到亚ns量级[4-5]。张小红等[4]在用GPS PPP方法进行时间传递时,时间比对精度达到0.1~0.2 ns,这与IGS“真值”标称的时间同步精度0.1~0.2 ns相同[6]。Guang等[7]用北斗载波相位法(BDS carrier phase,BDS CP)进行时间传递研究,采用北斗广播星历,证明BDS CP时间传递的精度比BDS CV高。本文利用武汉大学发布的精密卫星轨道和精密卫星钟差产品,以及甘肃省卫星定位连续运行基准站(continuously operating reference station,CORS)网4个站3 d的观测数据进行基于BDS PPP的时间传递研究,并将BDS PPP方法所得结果与GPS PPP方法进行了对比。结果表明,BDS CP时间传递精度与GPS CP在亚ns量级上是相当的。
1 BDS CP时间传递方法数学模型BDS CP算法采用的是精密单点定位解算模型,为了消除电离层影响,采用无电离层双频组合观测值,其数学模型可以表示为[4, 8]:
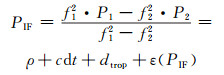
|
(1) |
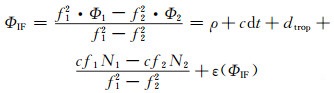
|
(2) |
式中,PIF为伪距无电离层组合值;f1和f2分别为两种载波的频率;P1和P2分别为两个频率的伪距观测值;ρ为星站间几何距离;dt为接收机钟差;ε(PIF)为伪距无电离层组合的其他综合误差;ΦIF为载波无电离层组合值;Φ1和Φ2分别为两个频率的相位观测值;N1和N2分别为两个频率的整周模糊度;ε(ΦIF)为载波无电离层组合的其他综合误差;dtrop为对流层延迟改正,可以表示为:
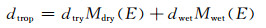
|
(3) |
式中,ddry、dwet分别为对流层延迟干分量和对流层延迟湿分量,M(E)代表与卫星高度角E有关的投影函数。为更好地消除对流层误差的影响,对流层干分量延迟采用Saastamoinen模型进行修正,而对流层湿分量延迟采用分段参数估计的方法进行估计,最后利用全球投影函数模型GMF[9]求得投影系数,并将其投影至卫星信号传播路径方向。
为得到时间传递监测站的观测方程,将式(1)和式(2)线性化[6]:
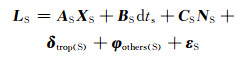
|
(4) |
式中,LS为组合观测值;AS和BS为系数矩阵;XS为监测站S的坐标;dts为接收机钟差;CS形式为[0 I]T;NS为组合观测值的模糊度;δtrop(S)为组合观测值的对流层延迟;φothers(S)为其他误差总和,其中包含相对论效应、地球自转改正、固体潮、海潮改正、卫星和接收机天线相位中心改正等;εS为残差[10-11]。
精密单点定位参数估计方法通常采用卡尔曼滤波或序贯平差的方法[12],本文采用卡尔曼滤波法进行计算。
2 数据处理及精度评估方法 2.1 数据准备实验选用甘肃CORS网4个站(A、B、C、D)的双频观测数据,观测时间为3 d(2013-11-24~11-26),采样间隔为15 s。选用武汉大学发布的事后精密星历和5 min间隔的精密卫星钟差产品进行求解。为适应本文数据处理的要求,对开源的RTKLIB中PPP钟差估计模块进行修改,包括周跳探测、数据质量控制等。改进后PPP定位精度为1~2 cm。本文在解算接收机钟差时采用固定测站坐标的方式。
2.2 数据预处理数据预处理主要是进行周跳探测,步骤如下:1)用M-W方法判断是否有周跳或粗差;2)利用电离层残差法对步骤1)的结果进行补充探测;3)采用多项式拟合法对疑似发生周跳的历元进行检核,作出最终判断。由于周跳修复较为困难且不是时间传递工作的重点内容,故本文采取只探测不修复的策略,在发生周跳的历元增加一个模糊度参数进行估计[4]。
2.3 参数估计本文静态PPP算法中,待估参数主要包括接收机钟差参数、模糊度参数、对流层延迟参数。参数估计采用卡尔曼滤波法,由于文中采用的是静态定位,位置参数被描述为不变的,因此在卡尔曼滤波时相应的状态噪声矩阵中对应位置取0;天顶方向对流层湿延迟参数初始值由Saastamoinen模型求得,对应的状态噪声系数取经验值10-8m2;接收机钟初始值为单点定位解的钟差,状态噪声系数取经验值900 m2。
2.4 精度评估方法由于GPS CP时间传递方法所能达到的精度为0.1~0.2 ns,与IGS“真值”标称的时间同步精度0.1~0.2 ns相当,故本文将BDS CP法所得结果与GPS CP法所得结果进行对比分析,将BDS CP方法与GPS CP方法之差的RMS作为评定BDS CP时间传递精度的依据。
3 算例分析为了验证算法的稳定性,本实验设计了两条对比链路:1)链路A-B,距离约62 km;2)链路C-D,距离约70 km。采用以下两种处理方案进行分析。
方案1:在两个测站上分别进行单站GPS PPP计算,得到两个测站的接收机钟差。对两个测站的接收机钟差作差,即为测站间的时间传递结果(GPS CP算法)。
方案2:在两个测站上分别进行单站BDS PPP计算,得到两个测站的接收机钟差。对两个测站的接收机钟差作差,即为测站间的时间传递结果(BDS CP算法)。
需要说明的是,本文所用的原始观测数据采样间隔为15 s,实际的时间同步中不需要如此高采样率的钟差序列。为此,采用每5 min输出一个钟差,所以方案1和方案2中所得的是5 min的离散钟差序列。分析方案1和方案2所得结果的差异,进而评估GPS CP算法与BDS CP算法在时间传递中的差异。
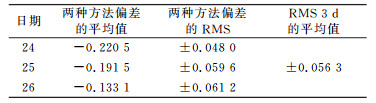
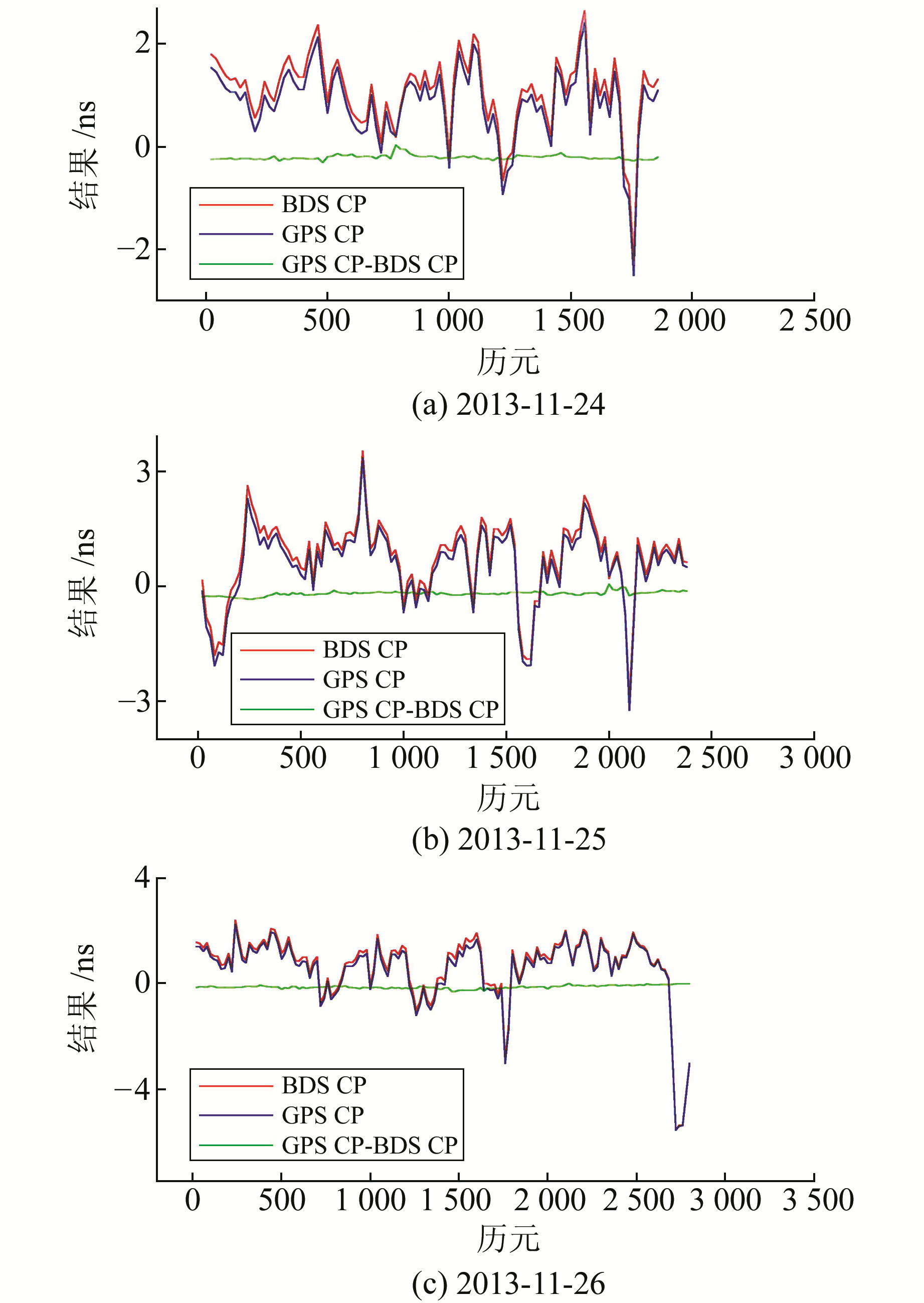
首先分析链路A-B上两种算法之间的差异情况,如图 1所示(图中红色线条表示用BDS CP法计算得到的A、B两站接收机钟差之差;蓝色线条表示GPS CP法计算得到的A、B两站接收机钟差之差;绿色线条表示两种方法所得结果的差值)。对比图 1(a)、图 1(b)、图 1(c)BDS CP法和GPS CP法的结果发现,红、蓝线条走势几乎完全一致,且代表两种方法差值的绿色线条几乎为一条水平直线,由此可以知道两种方法的时间传递能力是相当的。A-B链路3 d的实验结果数值统计见表 1(单位ns)。
|
图 1 链路A-B两种算法结果之间的差异 Fig. 1 Difference between results with two methods (A-B) |
|
|
表 1 链路A-B最终结果数值统计 Tab. 1 Numerical statistics of A-B |
由表 1可以看出,3 d内链路A-B中两种方法差值的RMS分别为±0.048 0 ns、±0.059 6 ns、±0.061 2 ns,3 d的RMS平均值为±0.056 3 ns。
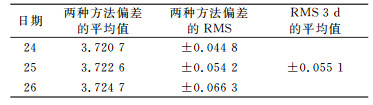
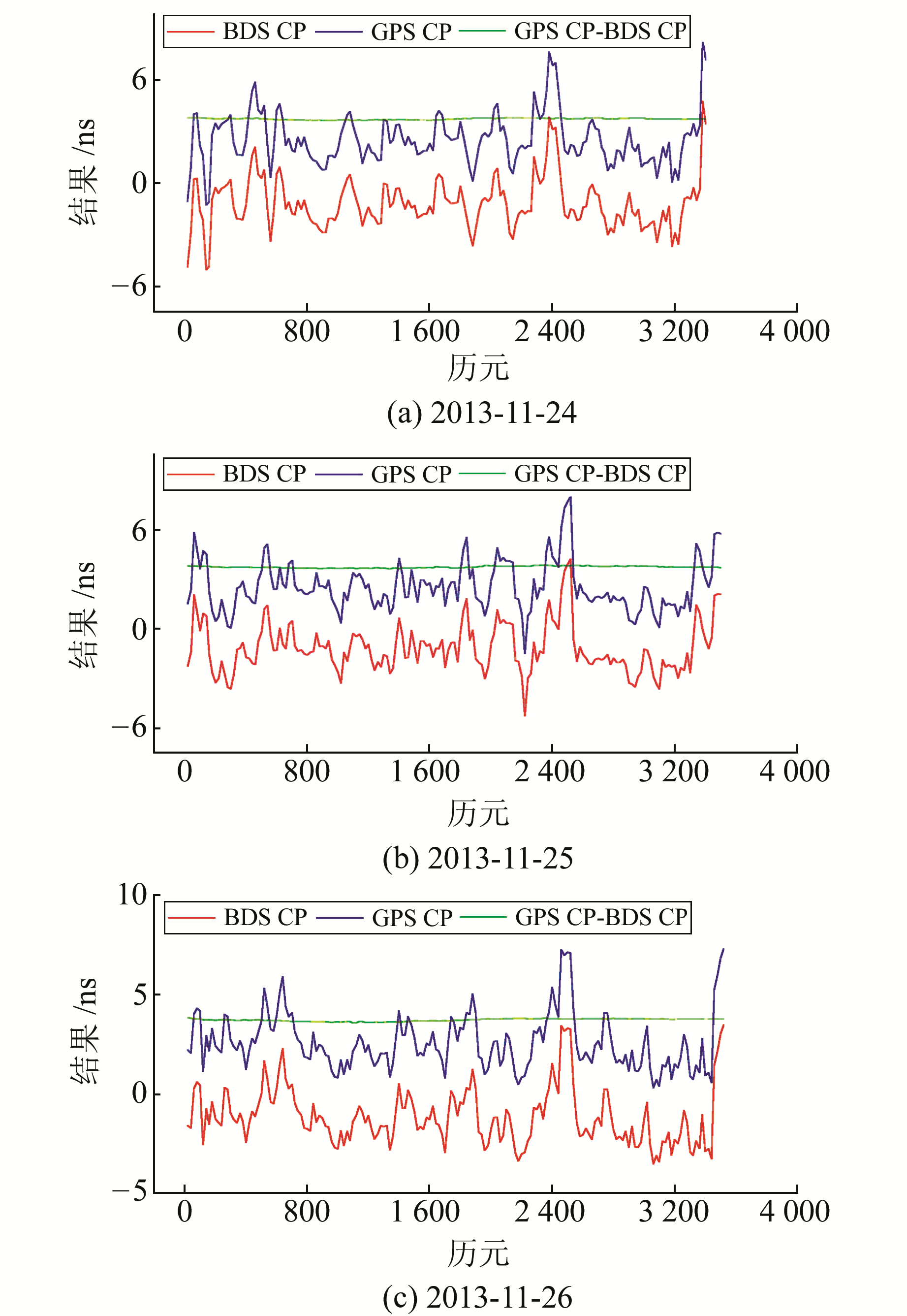
为进一步验证链路A-B所得的结论,对链路C-D按照相同的方案进行处理,如图 2所示。与图 1类似,通过对比分析同样可以得出BDS CP法和GPS CP法的时间传递能力相当。链路C-D中3 d的实验结果数值统计见表 2(单位ns)。
|
图 2 链路C-D两种算法结果之间的差异 Fig. 2 Differences between results with two methods (C-D) |
|
|
表 2 链路C-D最终结果数值统计 Tab. 2 Numerical statistics of C-D |
由表 2可以看出,3 d内链路C-D中两种方法差值的RMS分别为±0.044 8 ns、±0.054 2 ns、±0.066 3 ns,3 d的RMS平均值为±0.055 1 ns。
对比表 1和表 2可以发现,对于链路A-B和链路C-D,BDS CP法所得结果与GPS CP法所得结果之间偏差的RMS分别为±0.056 3 ns和±0.055 1 ns,说明两种方法所得结果之间的偏差波动很小,而GPS CP法时间传递的精度为0.1~0.2 ns,因此在亚ns这个量级上可以认为两种方法的精度是相当的。
另外,比较表 1和表 2的第2列可以发现,在不同的链路上,两种方法所得结果偏差的平均值不是固定的,而且差别较大,这可能是由于不同接收机对GPS信号和BDS信号的硬件延迟不同或系统间偏差造成的,但这并不影响用二者偏差的RMS评估它们在时间传递精度上的差异。
4 结语本文对BDS CP法时间传递模型进行详细阐述,并对其时间传递精度进行对比分析。通过两个不同链路的实验结果可以看出,BDS CP法与GPS CP法之差的RMS大约在±0.055 ns,而GPS CP法时间传递的精度在亚ns量级,因此在亚ns量级上可以认为BDS CP法和GPS CP法时间传递的精度基本相当。
| [1] |
杨帆.基于北斗GEO和IGSO卫星的高精度共视时间传递[D].北京: 中国科学院大学, 2013 (Yang Fan. High-Precision Common View Time Transfer Based on Beidou GEO and IGSO Satellites[D]. Beijing: University of Chinese Academy of Science, 2013)
(  0) 0) |
| [2] |
许国宏.北斗共视授时技术研究与设计[D].哈尔滨: 哈尔滨工程大学, 2007 (Xu Guohong. Research and Realization of Beidou Common-View Time Service Method[D]. Harbin: Harbin Engineering University, 2007)
(  0) 0) |
| [3] |
顾胜, 陈洪卿, 曾亮. 基于北斗-GNSS精密时频量值传递综述[J]. 宇航计测技术, 2012, 32(1): 41-44 (Gu Sheng, Chen Hongqing, Zeng Liang. Review of the Precise Traceability of Time and Frequency Based on Beidou/GNSS Transfer[J]. Journal of Astronautic Metrology and Measurement, 2012, 32(1): 41-44)
(  0) 0) |
| [4] |
张小红, 蔡诗响, 李星星, 等. 利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报:信息科学版, 2010, 35(3): 274-278 (Zhang Xiaohong, Cai Shixiang, Li Xingxing, et al. Accuracy Analysis of Time and Frequency Transfer Based on Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 274-278)
(  0) 0) |
| [5] |
张小红, 程世来, 李星星, 等. 单站GPS载波平滑伪距精密授时研究[J]. 武汉大学学报:信息科学版, 2009, 34(4): 463-465 (Zhang Xiaohong, Cheng Shilai, Li Xingxing, et al. Precise Timing Using Carrier Phase Smoothed Pseudorange from Single Receiver[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 463-465)
(  0) 0) |
| [6] |
黄观文, 杨元喜, 张勤, 等. 一种单差观测值的连续实时载波相位时频传递方法[J]. 武汉大学学报:信息科学版, 2013, 38(9): 1018-1022 (Huang Guanwen, Yang Yuanxi, Zhang Qin, et al. A New Continuous Time and Frequency Transfer Algorithm Based on GPS Single Different Carrier Phase Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1018-1022)
(  0) 0) |
| [7] |
Guang W, Zhang P F, Yuan H B, et al. The Research on Carrier Phase Time Transfer of Beidou Navigation Satellite System [C]. European Frequency and Time Forum, Neuchatel, 2014
(  0) 0) |
| [8] |
陈宪东. 基于大地型时间传递接收机的精密时间传递算法研究[J]. 武汉大学学报:信息科学版, 2008, 33(3): 245-248 (Chen Xiandong. Precision Time Transfer Methods Based on Geodetic Time and Frequency Transfer Receivers[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 245-248)
(  0) 0) |
| [9] |
Boehm J, Niell A, Tregoning P, et al. The Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7): 1-4
(  0) 0) |
| [10] |
Ray J, Senior K. Geodetic Techniques for Time and Frequency Comparisons Using GPS Phase and Code Measurements[J]. Metrologia, 2005, 42(4): 215 DOI:10.1088/0026-1394/42/4/005
(  0) 0) |
| [11] |
Defraigne P, Petit G. Time Transfer to TAI Using Geodetic Receivers[J]. Metrologia, 2003, 40(4): 184 DOI:10.1088/0026-1394/40/4/307
(  0) 0) |
| [12] |
黄观文. GPS精密单点定位和高精度GPS基线网平差研究及软件实现[D].西安: 长安大学, 2008 (Huang Guanwen. Research on GPS Precise Point Positioning and Adjustment of High Precision GPS Baseline Network and the Realization of Its Software [D]. Xi'an: Chang'an University, 2008))
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37