随着Beidou和Galileo系统的发展以及GLONASS的现代化,利用多系统进行精密单点定位(PPP)受到越来越多的关注。国内外学者对GPS/GLONASS、GPS/BDS以及四系统融合精密单点定位的性能进行了大量研究[1-6]。结果表明,多系统组合以后,可见卫星数大大增加,卫星的几何结构更强,可以显著改善单GPS系统收敛时间过长的问题,并且在较高卫星截止高度角的条件下,依然能够保证足够的可见卫星,从而改善山区、城市以及遮挡严重地区的定位精度。本文对比分析了单系统、多系统融合PPP的定位模型、收敛速度、静/动态定位结果以及不同截止高度角下单系统和多系统的定位结果。
1 多系统融合PPP模型及数据处理策略 1.1 基本观测方程基于双频无电离层组合的PPP观测方程为:
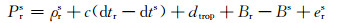
|
(1) |
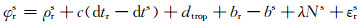
|
(2) |
式中,r和s分别代表测站和卫星,ρrs为卫星到测站的几何距离,dtr为接收机钟差,dts为卫星钟差,dtrop为对流层延迟,λ为无电离层融合的波长,Ns为无电离层组合模糊度, Br、br分别为接收机端无电离层组合伪距和相位的硬件延迟,Bs、bs分别为卫星端无电离层组合伪距和相位的硬件延迟,ers和εrs分别为伪距和相位上其他各项误差之和。IGS提供的精密卫星钟差产品包含Br的影响,而接收机端伪距硬件延迟Br则被吸收到接收机钟差中,即
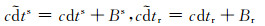
|
(3) |
将式(1)、(2)改写为:
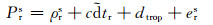
|
(4) |
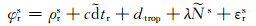
|
(5) |
式中,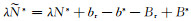
扩展到多系统的定位模型,可以表示为:
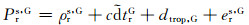
|
(6) |
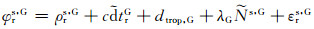
|
(7) |
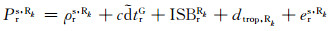
|
(8) |
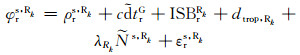
|
(9) |
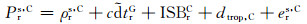
|
(10) |
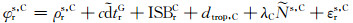
|
(11) |
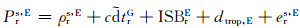
|
(12) |
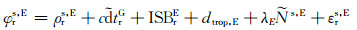
|
(13) |
其中,
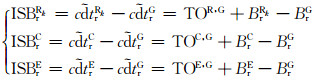
|
(14) |
式中,G、R、C、E分别代表GPS、GLONASS、Beidou、Galileo系统,k为GLONASS卫星的频率号(-7~+6),ISB为系统间偏差,TO为不同系统间固有的时间差。
从式(14)可以看出,ISB包含了系统间的时间差以及不同系统伪距硬件延迟之差。由于GLONASS采用频分多址的信号结构,不同的卫星信号频率不同,因此在GPS-GLONASS ISB中还包含了频间偏差(IFB)。为了对IFB进行补偿,本文根据GLONASS卫星频率设置了不同的ISB参数。而Beidou和Galileo采用和GPS相同的码分多址信号,其ISB只与测站有关,在处理时只需设置一个ISB参数。
1.2 数据处理策略采用扩展卡尔曼滤波进行参数估计。待估参数为测站坐标、接收机钟差、天顶对流层湿延迟、各个卫星的模糊度参数以及各系统相对于GPS的ISB参数。对流层湿延迟的随机模型采用随机游走模型,测站坐标随机模型在静态定位时采用常数模型,动态定位时采用白噪声模型,接收机钟差采用白噪声模型,对流层湿延迟模型采用随机游走,模糊度参数在连续弧段内作为常数,发生周跳时采用白噪声模型。ISB短期内比较稳定,1 d内作为常数处理[2]。卫星轨道和钟差采用GFZ的MGEX 15 min精密轨道和30 s精密钟差。卫星端和接收机端相位中心偏差(PCO)和天线相位中心变化(PCV)采用IGS发布的产品进行改正。目前IGS只提供Beidou和Galileo卫星端PCO,尚未提供接收机端的PCO和PCV,因此在处理Beidou和Galileo系统时只进行了卫星端PCO改正。同时,也考虑了极移、固体潮、海洋潮等改正。
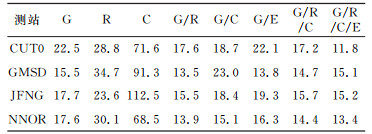
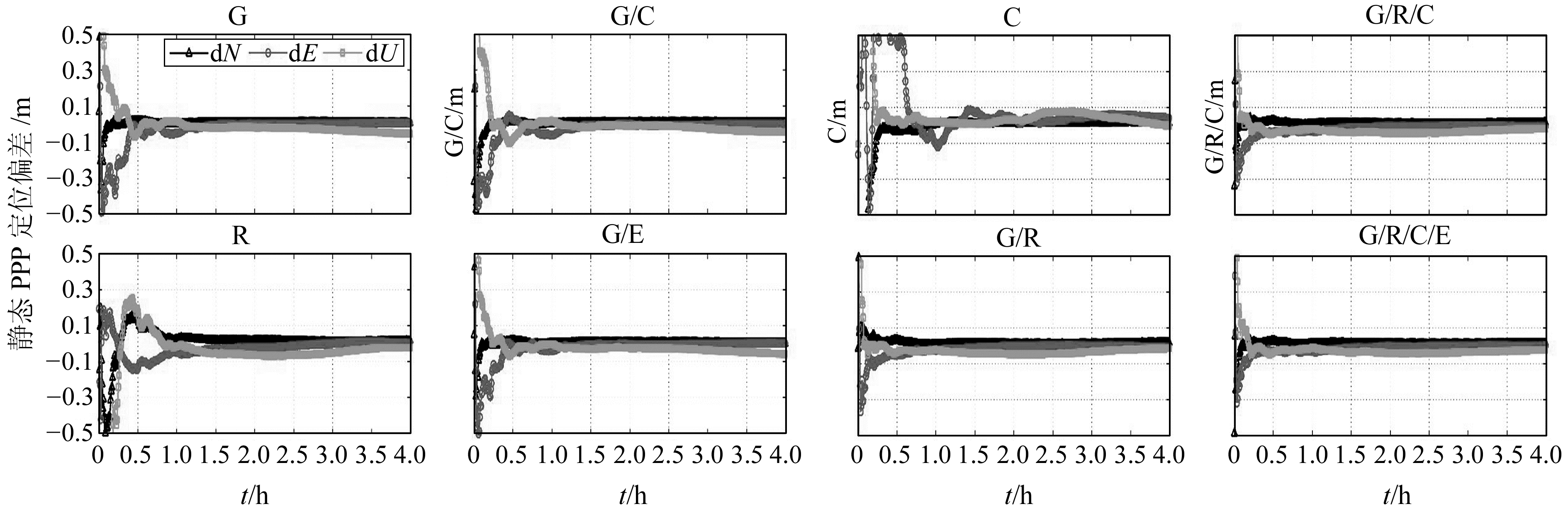
2 实验结果 2.1 静态PPP本文利用4个MGEX跟踪站2016年doy037的数据,采样间隔为30 s。将1 d的数据分为6个时段,每隔4 h重新初始化。定义收敛条件为N、E、U方向定位误差均小于0.1 m,并且其后20个历元定位误差也小于0.1 m。图 1给出了CUT0测站(-30.00°S,115.89°E,澳大利亚)8种定位模式下的第1个时段静态PPP定位偏差序列。可以看到,GPS收敛较快,约为23 min;GLONASS约为40 min;Beidou的收敛时间和GLONASS接近,约为39 min。G/R、G/C、G/E双系统融合都提升了单一系统的收敛速度,而G/R/C三系统融合和G/R/C/E四系统融合则进一步提高了收敛速度,四系统融合只需要8 min即可收敛。表 1给出了4个测站各时段收敛速度的平均值(单位min),表 2列出了各测站6个时段定位偏差RMS平均值(单位cm)。
|
图 1 CUT0站静态PPP定位偏差 Fig. 1 Positioning residuals of static PPP at station CUT0 |
|
|
表 1 各测站静态PPP收敛时间均值 Tab. 1 The mean value of convergence time in static PPP per station |
|
|
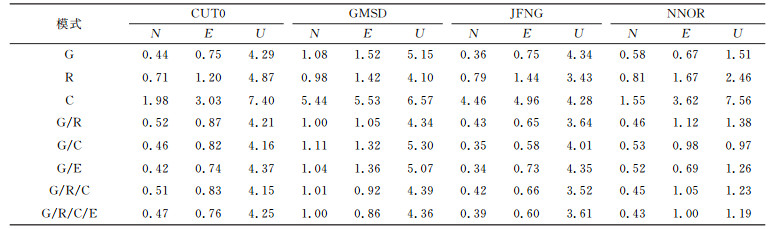
表 2 静态PPP定位偏差RMS均值 Tab. 2 Average RMS of positioning residuals in static PPP |
从表 1、表 2可以看出,GPS收敛速度较快,收敛后北向和东向精度在2 cm以内,天向精度一般不超过5 cm。GLONASS定位精度和GPS接近,但是收敛时间较长。Beidou的收敛时间明显比GLONASS更长,一般至少需要1 h。收敛后北向和东向精度不超过5 cm, 天向精度不超过8 cm。这一方面是因为Beidou的精密星历和精密钟差精度有限,另一方面是因为Beidou大多数为GEO和IGSO卫星,MEO卫星较少,几何图形强度不如GPS和GLONASS[4, 7-8]。而G/R、G/C、G/E融合的收敛速度均快于单系统,四系统融合的收敛速度最快,特别是CUT0测站,相较于单GPS系统,四系统融合的收敛速度提高了50%。在定位精度方面,多系统融合相对于GPS区别不大,在U方向有略微提升。
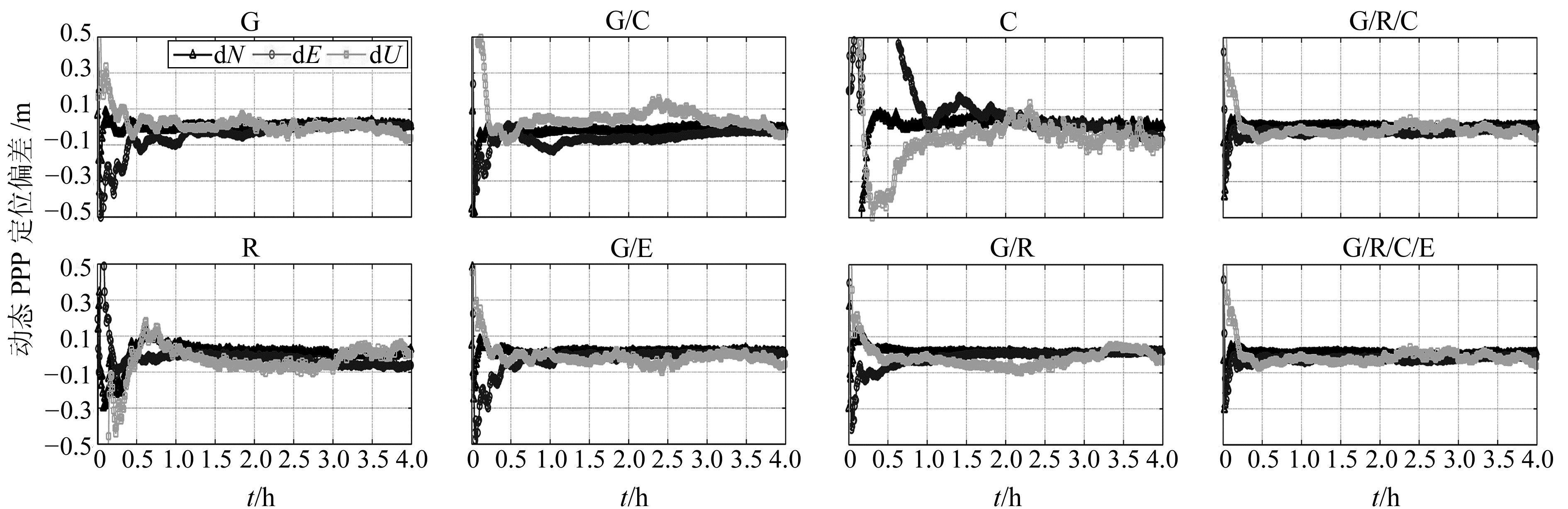
2.2 动态PPP图 2给出了CUT0站动态PPP定位偏差序列。GPS和GLONASS收敛时间都约为30 min。Beidou需要约60 min收敛,G/R/C/E四系统融合只需要11 min。
|
图 2 CUT0动态PPP定位偏差 Fig. 2 Positioning residuals of kinematic PPP at station CUT0 |
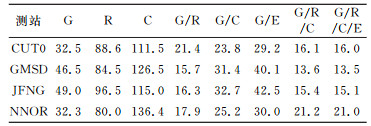
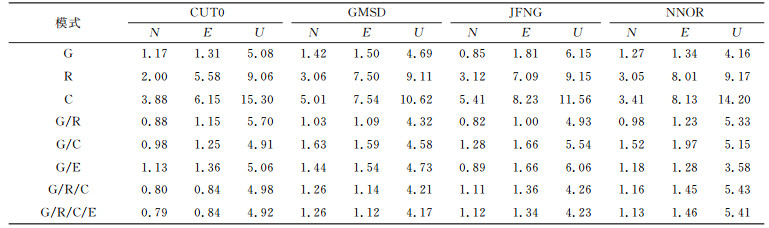
从表 3(单位min)、表 4(单位cm)可以看出,动态定位时,GPS收敛较快,定位精度较高。GLONASS收敛速度明显慢于GPS,定位精度也更差。Beidou平均收敛时间都在110 min以上,U方向定位偏差不超过16 cm。G/R、G/C、G/E融合的收敛速度比GPS更快,G/R/C/E四系统融合对收敛速度的提升非常显著。G/R/C三系统融合和四系统融合区别不大,主要是因为Galileo系统卫星数较少。在定位精度方面,四系统融合和GPS区别不大。
|
|
表 3 各测站动态PPP收敛时间均值 Tab. 3 The mean value of convergence time in kinematic PPP per station |
|
|
表 4 静态PPP定位偏差RMS均值 Tab. 4 Average RMS of positioning residuals in kinematic PPP |
图 3给出GMSD测站不同截止高度角下单GPS系统和四系统融合动态PPP的对比结果。从左至右,第1~4列分别对应截止高度角10°、20°、30°、40°的定位结果。可以看出,多系统融合可见卫星数量相较于单系统大大增加,在截止角为10°时,PDOP值一般不超过1.5,卫星几何结构更强。在截止高度角为40°时,GPS的可见卫星数在5颗以下,动态PPP的定位偏差也急剧增加,而多系统依然可以保证可见卫星数在10颗以上,从而保证可靠的定位精度。

|
图 3 GMSD测站不同截止高度角条件下动态PPP定位结果 Fig. 3 Comparisons of kinematic PPP under different cutoff elevations(from 10°to 40°) at station GMSD |
1) 静态定位时,GLONASS和GPS的定位精度相当,但收敛速度慢于GPS。Beidou由于轨道精度和几何构型的限制,定位精度和收敛速度差于GLONASS。四系统融合的收敛速度最快,定位精度和GPS相比没有明显提升。
2) 动态定位时,GLONASS的定位精度和收敛速度都略差于GPS,Beidou一般需要110 min收敛,收敛后平面精度优于8 cm, 高程精度优于16 cm。四系统融合对收敛速度的提升非常显著,定位精度和GPS接近。
3) 多系统可以明显改善山区、城市等卫星信号被严重遮挡地区的定位精度,尤其在截止高度角超过30°时,GPS系统出现较大的定位偏差,而多系统融合依然能够接收到足够数量的卫星,从而保证可靠的定位精度。
致谢: 感谢IGS提供MGEX观测数据,感谢GFZ提供MEGX精密轨道和钟差。
| [1] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2009 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [2] |
Li X X, Ge M R, Dai X L, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. J Geod, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
| [3] |
Cai C S, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations: GPS, Beidou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143 DOI:10.1016/j.asr.2015.04.001
(  0) 0) |
| [4] |
Bruyninx C. Comparsing GPS Only with GPS+GLONASS Positioning in a Regional Permanent GNSS Network[J]. GPS Solutions, 2007, 11(1): 97-106
(  0) 0) |
| [5] |
Li M, Qu L Z, Zhao Q L, et al. Precise Point Positioning with the Beidou Navigation Satellite System[J]. Sensors, 2014, 14(1): 927-943 DOI:10.3390/s140100927
(  0) 0) |
| [6] |
任晓东, 张柯柯, 李星星, 等. Beidou, Galileo, GLONASS, GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307-1313 (Ren Xiaodong, Zhang Keke, Li Xingxing, et al. Precise Point Positioing with Multi-Constellation Satelllite Systems:Beidou, Galileo, GLONASS, GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307-1313)
(  0) 0) |
| [7] |
屈立忠, 赵齐乐, 郭靖, 等. GNSS融合动态精密单点定位性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 298-302 (Qu Lizhong, Zhao Qile, Guo Jing, et al. Performance Analysis on Multi-GNSS Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 298-302)
(  0) 0) |
| [8] |
丁赫, 孙付平, 李亚萍, 等. BDS/GPS/GLONASS组合精密单点定位模型及性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 304-306 (Ding He, Sun Fuping, Li Yaping, et al. Modeling and Performance Analysis of Combined BDS/GPS/GLOANSS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 304-306)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37