2. 中国测绘科学研究院,北京市莲花池西路28号,100830;
3. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
GPS位置坐标时间序列噪声包含白噪声和与时间相关的有色噪声[1]。一般认为,卫星轨道误差、电离层和对流层影响、多路径效应、站点区域气候季节变化、地质构造活动、非构造形变等因素会产生有色噪声[2]。与此同时,区域的GPS站点坐标时序间存在一种来源尚不明确的时空相关的共模误差(common mode error, CME)[3-5]。共模误差的剔除通常采用区域叠加滤波、主成分分析(PCA)和改进主成分分析法(KLE)。殷海涛等[5]利用PCA/KLE结合的方法对四川CORS网进行共模误差的提取,虽然其中考虑了站点非均匀分布及局部效应的多样性,但所得结果的精度相较于区域叠加滤波只有略微提高,且其算法较为复杂。田云峰等[6]考虑到站点间距和总体相关性水平,对区域叠加滤波进行改进,虽然对大尺度GPS网的共模误差剔除效果较好,但对于小尺度而言其残差RMS也只改进了5%左右,且算法繁琐。
若站点附近发生地震,一般会在提取共模误差前将同震位移和震后弛豫形变去除,但拟合的坐标时序不可能将其完全剔除,最后得到的残差时序依然会含有地震的影响,而诸多文献在分析坐标时序噪声时几乎都未将地震影响考虑在内。本文以2011年东日本MS9.0大地震前后坐标时间序列数据为例,通过极大似然估计和相关评价准则,在多种噪声模型组合中确定地震前后基准站各分量最优噪声模型,研究并分析各基准站时序随机特性是否因为此次地震而发生显著变化,同时分析共模误差的特点及其对坐标时间序列噪声特性的影响。
1 最优噪声模型评价准则与数据处理策略当选取的噪声模型不同时,依据MLE方法原理可得到不同的极大似然对数值,数值越大,结果越可靠。但是不能简单地选取MLE值较大的模型组合作为最优噪声模型,因为MLE值越大, 模型中的参数也越多[7]。本文依据Langbein保守估计准则来选取最优噪声模型。首先选取两组模型并计算其MLE值,MLE值较大者作为零假设。将另外的模型组合的MLE值与零假设进行对比,若MLE差值大于2.6,则拒绝零假设,反之则接受。接受带通+幂律噪声模型的阈值设为2.6,接受一阶高斯马尔科夫+随机漫步噪声模型的阈值为5.2[7-8]。
在数据解算之前,需根据GPS站点非线性运动模型原理[1],在震后坐标时序中剔除同震位移和呈对数形式的震后弛豫形变,以便提取较为精确的残差时序,并以此计算共模误差的大小。对于共模误差的剔除,本文采用区域叠加滤波法[9-12]。
一般认为白噪声+闪烁噪声是描述GPS时间序列噪声比较恰当的模型[1-2, 6, 8]。但Langbein[7, 13]发现,坐标时间序列中还包含有一阶高斯-马尔科夫噪声和带通滤波噪声,并在美国南加州等地检测到此类噪声。因此,本文选取白噪声+闪烁噪声(WN+FN)、白噪声+随机游走噪声(WN+RWN)、白噪声+闪烁噪声+随机游走噪声(WN+FN+RWN)、白噪声+幂律噪声(WN+PL)、带通滤波噪声+幂律噪声(BP+PL)、一阶高斯-马尔科夫噪声+随机漫步噪声(FOGM+RWN)共6种组合噪声模型进行分析。
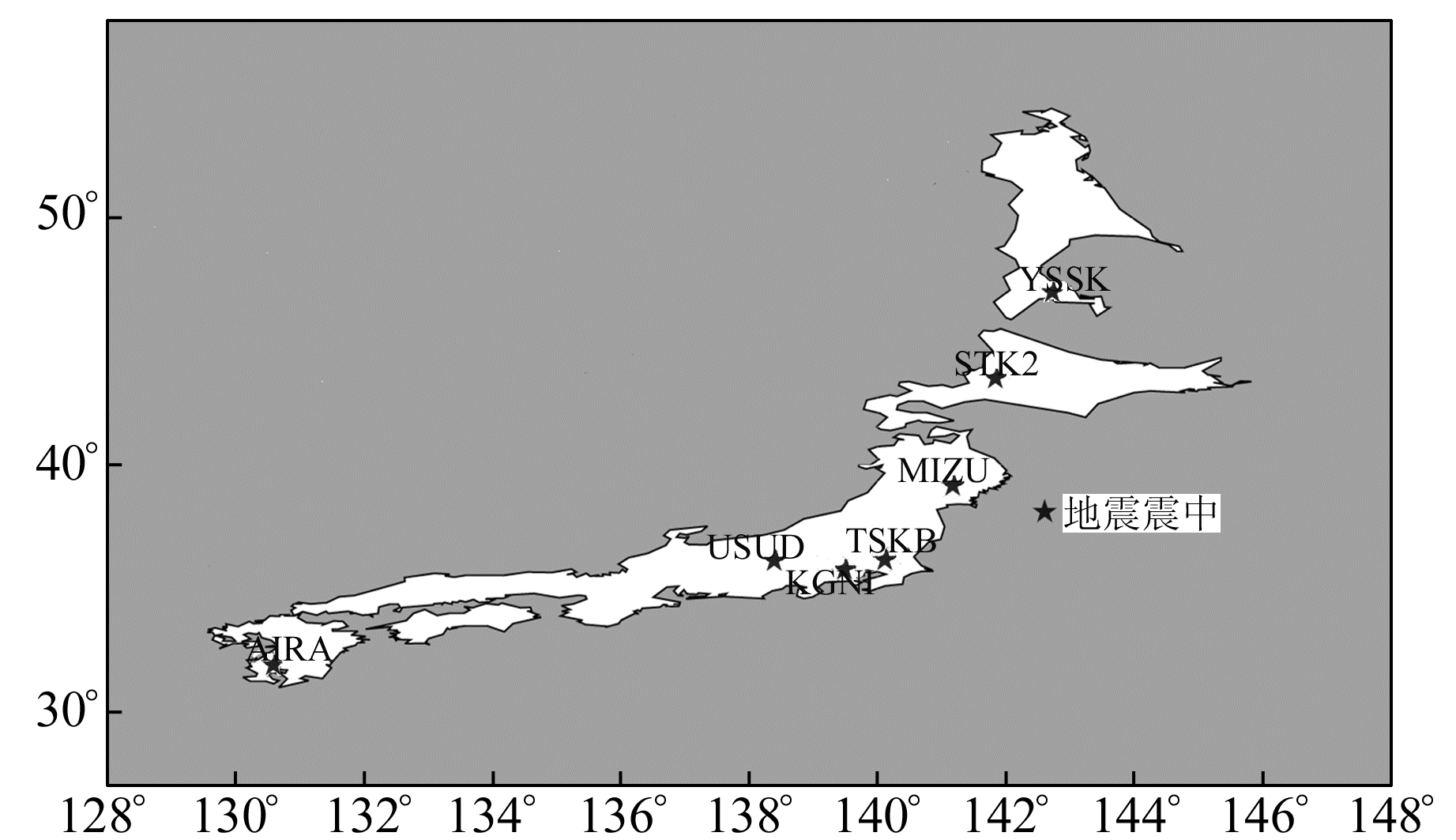
MLE方法不仅可以分析噪声类型,还可对噪声大小进行估计[11, 14-15]。本文将采用基于MLE方法的CATS软件,对图 1所示的日本7个IGS站点(AIRA、KGNI、MIZU、STK2、TSKB、USUD、YSSK)进行噪声分析,以研究共模误差剔除和东日本大地震前后噪声特性的变化,并从中选取最佳噪声模型。
|
图 1 IGS站点分布 Fig. 1 The distribution map of IGS site |
为了避免共模误差对坐标时间序列分析的影响,本文采用区域叠加滤波方法将其剔除。
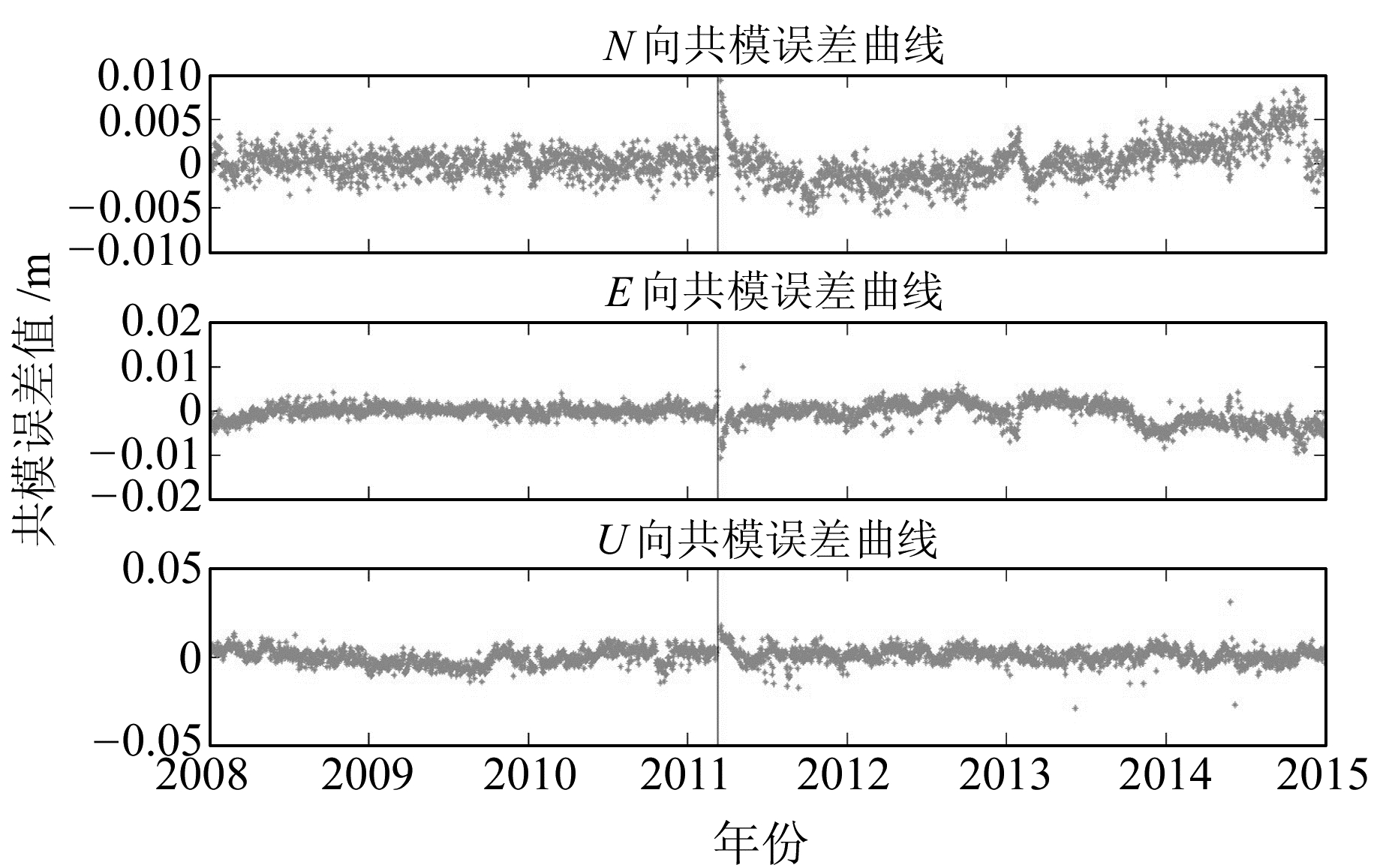
图 2为站点区域7 a的共模误差曲线,竖线为地震时刻;图 3为2008年下半年共模误差拟合曲线。可以看出:
|
图 2 N、E、U向共模误差曲线 Fig. 2 The common mode error curve of N, E, U direction |
|
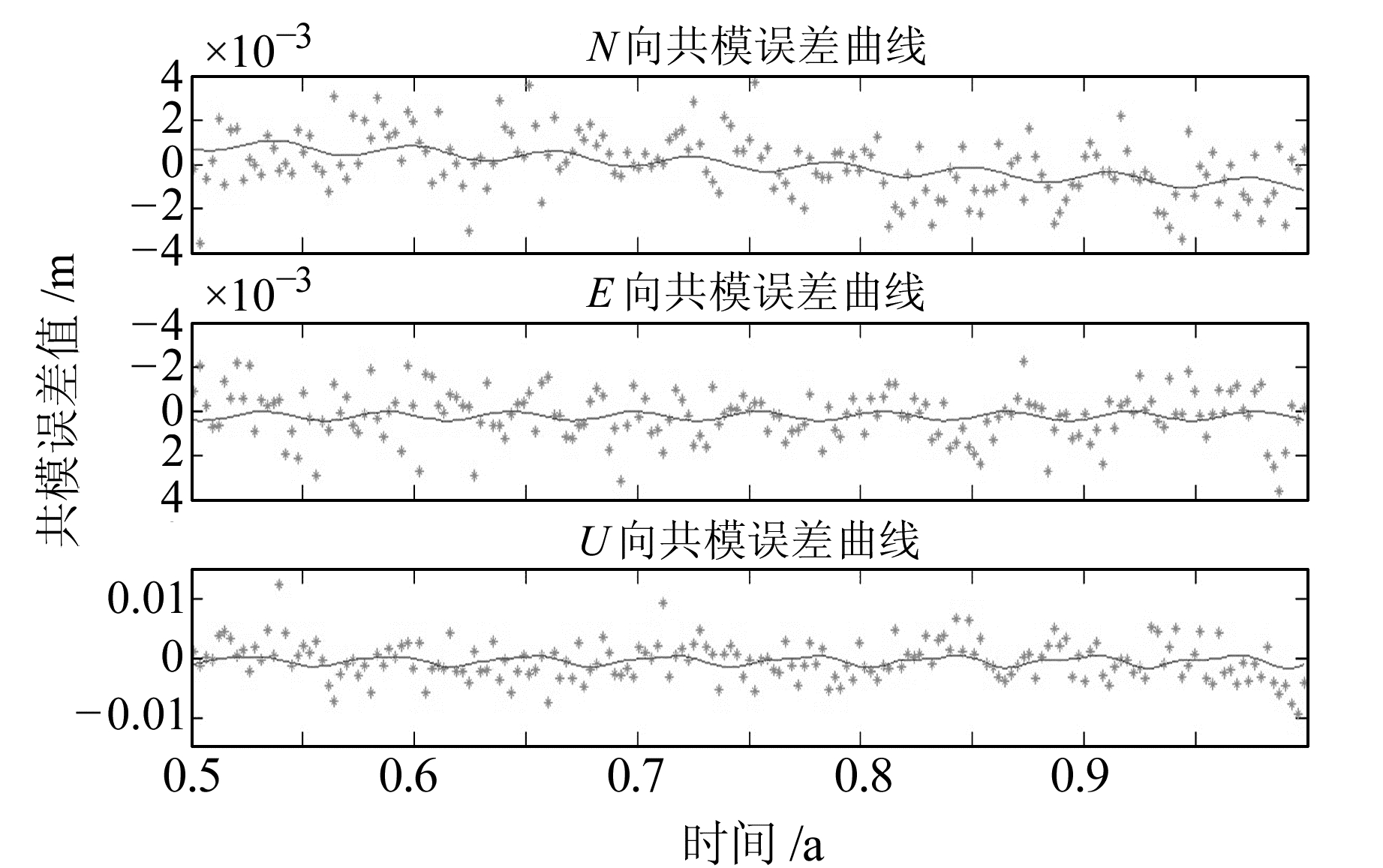
图 3 2008年下半年共模误差拟合曲线 Fig. 3 The fitting curve of common mode error in the latter half of 2008 |
1) 共模误差在N、E、U向均表现出较为明显的周期特性,地震之后E向周期特性尤为明显。
2) 地震发生后共模误差会发生对数形式的变化,之后逐渐趋向于震前水平, 这里可能存在未被完全剔除的震后弛豫形变的影响。
3) 震前共模误差N、E、U向均值分别为0.06 mm、0.13 mm、0.35 mm,而震后各方向均值皆有所增大,U向增加近1.5倍,为0.82 mm;其次为N向的0.19 mm,增加2倍多;变化最小的为E向的0.15 mm,与震前基本相近。
虽然共模误差来源尚不明确,但利用区域叠加滤波的方法能较好地将其剔除。当发生地震时,地震对共模误差的影响也应充分考虑,以提高IGS基准站坐标的精度。
2.2 共模误差对坐标时序噪声的影响从图 2、3中可以看出,在不同方向上共模误差表现出不一样的特性, 其在N、E、U向的最大值分别为10.65 mm、9.36 mm、15.35 mm;共模误差的周期特性在各方向也有差异,N、U向为明显的短周期特性,而E向在震后则表现出非常明显的长周期特性,且周期振幅增大明显;地震发生时,共模误差在各方向表现出与震后弛豫形变相似的变化规律,这其中可能含有未被完全剔除的震后弛豫形变的影响。
剔除共模误差后,IGS站点坐标时序的均方根有较明显的降低。各站震前N、E、U向坐标时序平均均方根相较于滤波前分别减小48%、41%、32%,震后则减小更多,分别为57%、49%、40%。因此,利用区域叠加滤波去除共模误差后,IGS基准站坐标的可靠性和精确性将得到较大提高。
除了震前USUD站以及震后MIZU站的N、E向最优噪声模型在剔除共模误差前后未变化外,其他大部分站点3个方向的最优噪声模型均有变化。图 4、图 5为剔除共模误差前后最优噪声模型分布图,纵轴表示最优噪声模型的个数。可以看出,共模误差剔除后,BP+PL比例明显下降(震前降幅40%,震后降幅62%),PL+WN比例增加,而FN+WN比例在地震前后截然相反,这很可能是地震影响所致。

|
图 4 剔除共模误差前后的震前最优噪声模型分布 Fig. 4 Before and after the elimination of the common mode error, optimal noise model distribution before earthquake |
|
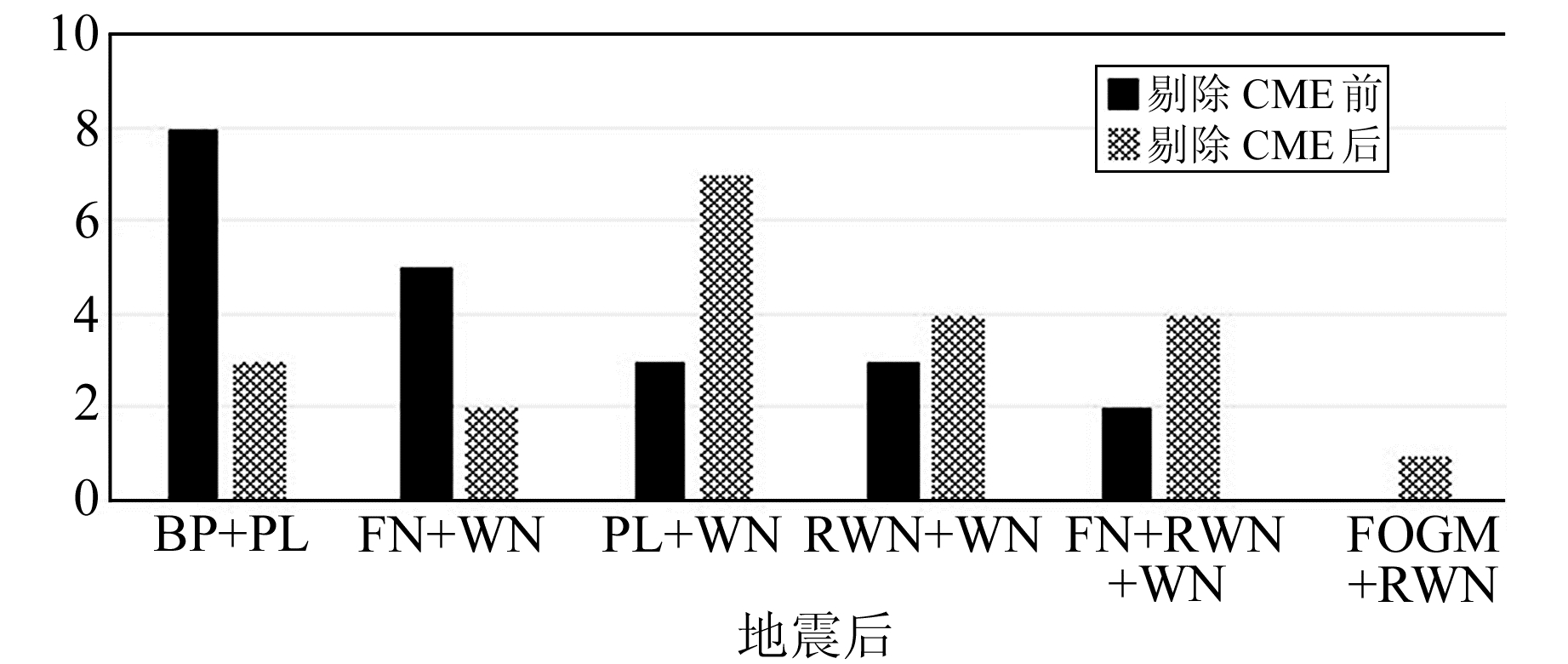
图 5 剔除共模误差前后的震后最优噪声模型分布 Fig. 5 Before and after the elimination of the common mode error, optimal noise model distribution after earthquake |
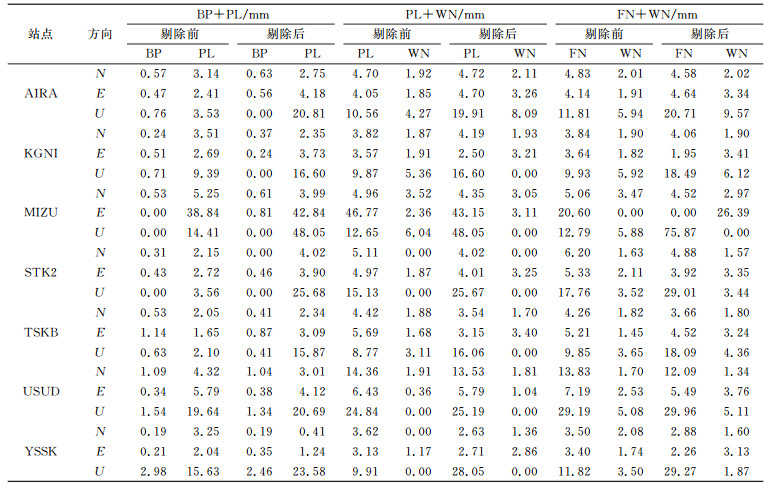
为了更好地理解共模误差剔除前后最优噪声模型的分布变化及其对坐标时序噪声的影响,此处只列出震前3个主要最优噪声模型在共模误差剔除前后的噪声参数估值,以排除地震的影响。如表 1所示,共模误差剔除后:1)除MIZU、STK2站U方向不存在BP及距震中较远的AIRA、YSSK站N、E方向BP增大外,其他站点各方向BP均有减小,这与BP+PL比例下降明显一致。2)在BP+PL模型中,除YSSK在N、E向的PL估值减小外,其他站点各方向PL均明显增大;而在PL+WN中,AIRA站N、E向和所有站点U方向的PL增大明显,其他站点各方向皆减小,几乎成相反的变化,说明共模误差剔除后,BP的存在掩盖了大部分站点N、E向PL的减小趋势。3)各基准站U方向的FN均增大,而绝大多数站点N、E方向的FN均有较明显减小,这与空间滤波可分离空间相关噪声、且主要削弱水平方向闪烁噪声的结论是一致的[12-13]。
|
|
表 1 剔除共模误差前后的震前主要最优噪声模型的噪声参数估值 Tab. 1 Before and after the elimination of the common mode error, estimation of noise parameters of the main optimal noise model before the earthquake |
综上可知,共模误差剔除后带通滤波噪声(BP)与闪烁噪声(FN)均发生明显变化,谱指数为非整数的幂律噪声(PL)及随机漫步噪声(RWN)皆有增强。这再次说明,坐标时序中的幂律噪声指数并非都像WN、FN、RWN呈整数形式存在。同时,利用区域叠加滤波剔除共模误差后,可明显削弱水平方向的闪烁噪声(FN)。因此,在分析站点坐标时序的噪声特性时,具有空间相关性的共模误差的影响不可忽略,应予以剔除。
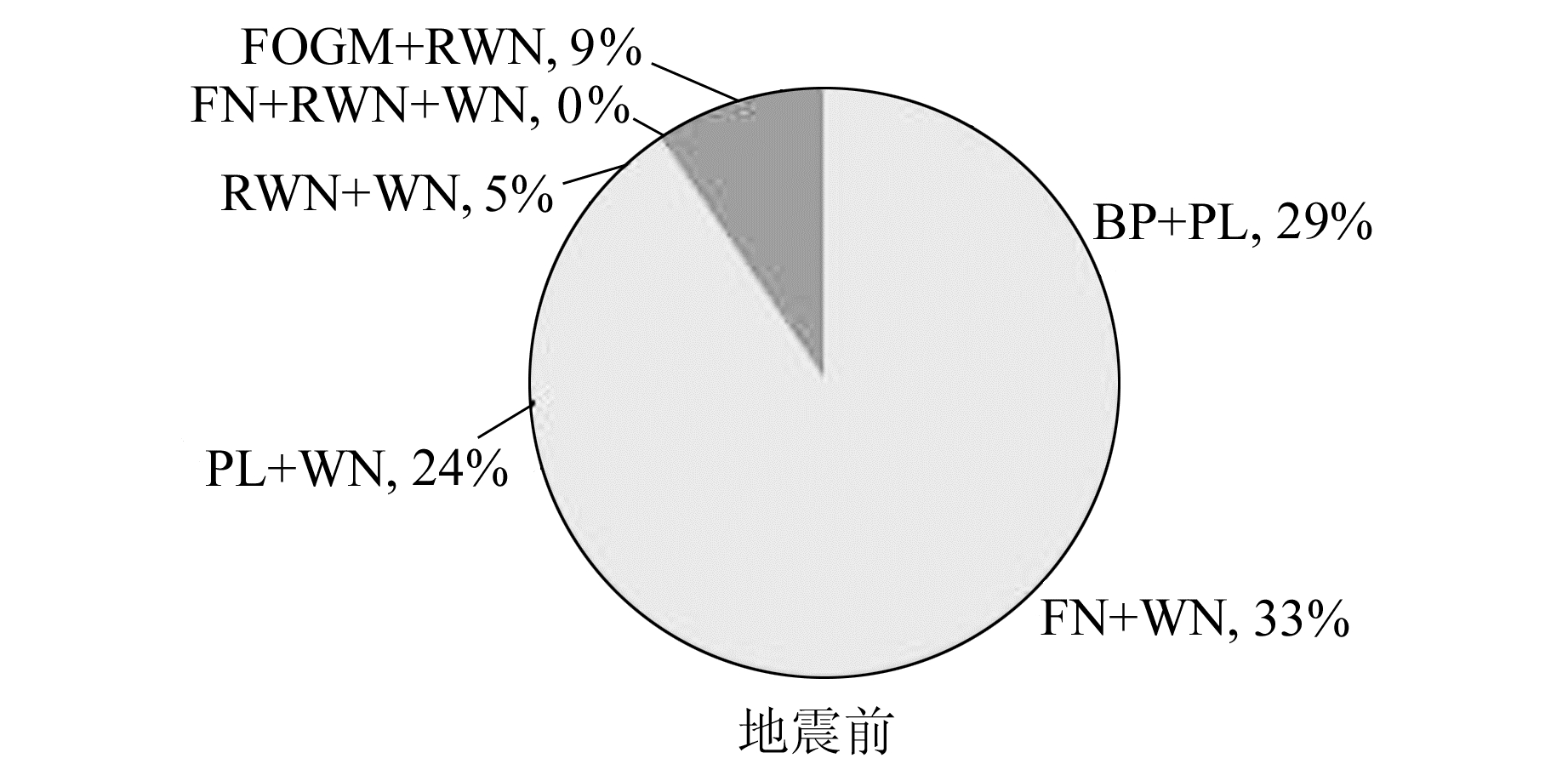
3 地震对坐标时序噪声的影响从表 2和图 6、图 7可以看出,除TSKB站E、U方向外,其他站点各方向最优噪声模型在震后全部发生变化,大部分基准站在3个方向的坐标分量的噪声特性均表现出较大差异。震前以BP+PL、FN+WN、PL+WN为主要噪声模型,而震后BP+PL和FN+WN比例明显降低,降幅分别达52%、69%,FOGM+RWN略有减小。FN+RWN+WN比例从0增加至19%,RWN+WN和PL+WN均有所增加,且成为主要噪声模型。
|
图 6 震前最优噪声模型分布 Fig. 6 The optimal noise model distribution before earthquake |

|
图 7 震后最优噪声模型分布 Fig. 7 The optimal noise model distribution after earthquake |
|
|
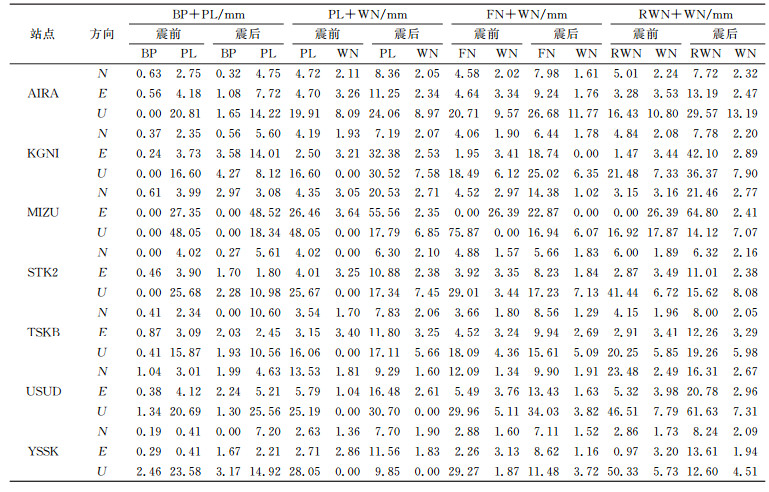
表 2 地震前后主要最优噪声模型的噪声参数估值 Tab. 2 Estimation of the noise parameters of the main optimal noise model before and after the earthquake |
如表 2所示,地震发生后基准站各方向噪声估值均有变化。除距震中较近的MIZU站点E、U向不存在BP外,绝大多数基准站各方向BP估值均明显增大;而对于PL估值,除MIZU、YSSK站U向明显降低外,其他站点各方向均呈增大趋势;除距震中较近的MIZU、STK2、YSSK、TSKB站点U方向FN、RWN降幅近50%外,几乎所有站点各方向的FN、RWN均有增大;而在大多数噪声模型中均有考虑的WN,其在E方向近乎全部减小,N、U方向均呈增大趋势。
由此可以看出,基准站坐标各分量表现出不同的噪声特性,U方向噪声明显大于N、E方向,这与普遍认为的垂直方向精度低于水平方向的结论是一致的。地震能较明显地削弱大部分站点U方向的闪烁噪声(FN)和随机漫步噪声(RWN),同时能引起谱指数为非整数的幂律噪声(PL)以及带通滤波噪声(BP)的增强,且距震震中越近,其对基准站坐标各分量噪声特性的影响越明显。
闪烁噪声(FN)主要归因于空间相关的物理性偏差, 而区域叠加滤波可以大幅削弱闪烁噪声[5, 14]。在剔除共模误差之后,地震依然明显降低了大部分站点U方向的闪烁噪声,并使其在水平方向增大。虽然目前地震对闪烁噪声的影响机制还不明确,但其影响不可忽视,应充分考虑。
目前,随机漫步噪声(RWN)一般认为是源自天线墩的运动,受外部温度、土壤水分、气候以及地质构造活动等因素影响[16]。由以上分析可知,地震发生后,许多站点均出现RWN增大的现象。虽然外部温度、太阳照射、气压等因素可能导致天线墩的运动,从而使RWN增强,但是根据历年的数据分析可知,它们对天线墩的影响非常有限。所以地震等地质构造活动是引起站点天线墩运动、导致上述现象发生的重要因素。
本文选取的7个IGS站点中,地震对FOGM的影响不大。但地震均能较明显地增强BP和指数为非整数幂律噪声(PL),其影响均需考虑。
4 结语本文利用CATS软件计算了日本7个IGS基准站区域的共模误差,确定了地震前后站点各方向的最优噪声模型,并分析共模误差和东日本大地震对坐标时间序列噪声特性的影响,得出以下结论:
1) 日本7个IGS基准站N、E、U 3个方向坐标分量表现出不同的噪声特性,其变化因站而异,并未表现出明显的规律,最优噪声模型主要表现为BP+PL、FN+WN、PL+WN。
2) 在对IGS站点东日本大地震前后的坐标时序进行区域叠加滤波和剔除共模误差后,IGS站点坐标时序的均方根明显降低,IGS基准站坐标的可靠性和精确性得到较大提高。共模误差在各方向均表现出较为明显的周期特性,地震之后E方向周期特性尤为明显且振幅明显增大。地震的发生改变了共模误差的特性,其具体影响还需进一步研究。共模误差剔除后,大部分站点3个方向最优噪声模型均发生变化,BP+PL、PL+WN比例下降明显,PL、RWN得以增强,BP、FN均有明显变化,且水平方向的FN得到明显削弱。
3) 地震会使站点坐标时序噪声特性发生明显变化。震前站点以BP+PL、FN+WN、PL+WN为主要噪声模型,而震后BP+PL和FN+WN比例降幅明显,RWN+WN和PL+WN均有所增加,且成为主要噪声模型。
地震对站点坐标时序噪声的影响主要表现为BP、FN和RW特性。且距离震中越近,其对基准站坐标各分量噪声特性的影响越明显。而地震与共模误差对基准站坐标时序噪声中的FN影响结果几乎截然相反。
本文虽然得到了一些有益于探索噪声来源的结论,但在计算共模误差时未考虑站点区域范围和站间距离大小,且时间序列只选择了地震前后各3 a;同时,本文中的结论仅基于2011年MS9.0东日本大地震,由地震类型及发震构造等因素而导致的差异并未考虑。
致谢: 感谢SOPAC提供IGS基准站坐标时间序列,感谢Williams博士提供CATS软件,感谢导师在数据处理方面的悉心指导。
| [1] |
黄立人. GPS基准站时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33 (Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31-33)
(  0) 0) |
| [2] |
蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355-363 (Jiang Zhihao, Zhang Peng, Bei Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 355-363)
(  0) 0) |
| [3] |
吕成亮, 张胜凯, 沈飞, 等. 基于共性误差的CORS站坐标时间序列分析[J]. 大地测量与地球动力学, 2016, 36(1): 16-20 (Li Chengliang, Zhang Shengkai, Shen Fei, et al. The Analysis of Coordinate Time Series of CORS Based on Common Mode Errors[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 16-20)
(  0) 0) |
| [4] |
伍吉仓, 孙亚峰, 刘朝功. 连续GPS站坐标时间序列共性误差的提取与形变分析[J]. 大地测量与地球动力学, 2008, 28(4): 97-101 (Wu Jicang, Sun Yafeng, Liu Chaogong. Extraction of Common Mode Erros for Continuous GPS Network and Deformation Analysis[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 97-101)
(  0) 0) |
| [5] |
殷海涛, 甘卫军, 熊永良, 等. PCA空间滤波在高频GPS定位中的应用研究[J]. 武汉大学学报:信息科学版, 2011, 36(7): 825-829 (Yin Haitao, Gan Weijun, Xiong Yongliang, et al. Study on the Effect of PCA Spatial Filtering on High-rate GPS Positioning[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 825-829)
(  0) 0) |
| [6] |
田云峰, 沈正康. GPS观测网络中共模分量的相关加权叠加滤波[J]. 地震学报, 2011, 33(2): 198-208 (Tian Yunfeng, Shen Zhengkang. Correlation Weighted Stacking Filtering of Common-Mode Component in GPS Observation Network[J]. Acta Seismologica Sinica, 2011, 33(2): 198-208 DOI:10.3969/j.issn.0253-3782.2011.02.007)
(  0) 0) |
| [7] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research Atmospheres, 2008, 113(B5): 620-628
(  0) 0) |
| [8] |
李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503 (Li Zhao, Jiang Weiping, Liu Hongfei, et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica, 2012, 41(4): 496-503)
(  0) 0) |
| [9] |
Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18057-18070 DOI:10.1029/97JB01378
(  0) 0) |
| [10] |
Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego: University of California, 2002
(  0) 0) |
| [11] |
田云峰. GPS位置时间序列中的中长期误差研究[D].北京: 中国地震局地质研究所, 2011 (Tian Yunfeng. Study on Intermediate and Long Term Errors in GPS Position Time Series[D].Beijing: Institute of Geology, CEA, 2011)
(  0) 0) |
| [12] |
田云峰, 沈正康. GPS坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68-81 (Tian Yunfeng, Shen Zhengkang. Progress on Reduction of Nontectonic Noise in GPS Position Time Series[J]. Acta Seismologica Sinica, 2009, 31(1): 68-81 DOI:10.3321/j.issn:0253-3782.2009.01.008)
(  0) 0) |
| [13] |
Langbein J. Noise in Two-Color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B4)
(  0) 0) |
| [14] |
Williams S D P, Bock Y, Fang P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [15] |
Williams S D P. CATS:GPS Coordinate Time Series Analysis Software[J]. GPS Solutions, 2008, 12(2): 147-153 DOI:10.1007/s10291-007-0086-4
(  0) 0) |
| [16] |
Zhang J, Bock Y, Johnson H, et al. Southern Califonia Permanent GPS Geodetic Array:Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18035-18053 DOI:10.1029/97JB01380
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China;
3. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2017, Vol. 37
2017, Vol. 37