2. 78125部队,成都市, 610066
北斗卫星三频信号的发播[1],使得三频情形下周跳的实时探测与修复更加可靠。针对组合观测量的选取,范建军等[2]与董丽娜等[3]分别给出了筛选三频周跳探测检测量的4个基本原则,并依此原则选取3个观测值组合作为周跳检验量,实现了三频非差观测数据周跳的自动探测与改正。基于以上选取原则与标准,熊伟[4]与Lacy等[5]分别利用模拟的三频GPS观测数据对三频伪距/载波相位组合法探测周跳展开研究。Dai等[6]选取电离层影响最小的两个几何无关检测量来探测周跳,然后通过估计几何项并结合最小二乘法、LAMBDA搜索法来确定周跳的大小。伍岳等[7]研究了多频数据组合在大采样率条件下对周跳的探测与修复,并得出多频数据组合可以实时探测出0.2周以上周跳值的结论。以上方法主要局限于GPS三频模拟数据,对于三频实测数据,尤其是北斗数据研究较少。基于北斗三频实测数据,李金龙[8]和谢凯等[9]研究比较了三频伪距相位组合和三频无几何相位组合周跳探测与修复的方法,得出伪距相位组合法明显受采样率及伪距噪声影响的结论。黄令勇等[10]针对三频无几何相位组合难以实时修复周跳的问题,提出利用两个无几何相位组合和一个三频伪距/载波组合联立方程组修复周跳的方法,并采用搜索法克服方程解不稳定的问题,表明周跳探测精度受电离层影响。
本文基于单差模型提出一种电离层残差辅助伪距相位组合周跳探测的方法,即通过优选组合确定3个线性无关的超宽巷宽巷组合(0, -1, 1)、(1, 4, -5)、(4, -2, -3),然后针对三频伪距相位法可能出现的误探情况采用电离层残差辅助周跳探测。
1 周跳探测模型 1.1 周跳探测三频伪距相位组合观测量方程可表示为[11]:
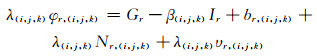
|
(1) |
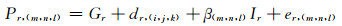
|
(2) |
式中,φr, (i, j, k)为以周为单位的载波相位观测量,Pr, (m, n, l)为以m为单位的伪距观测量,dr, (i, j, k)与br, (i, j, k)分别为伪距和载波硬件延迟偏差,Gr为与频率无关的几何项,Ir为频点f1上的一阶电离层延迟,β(i, j, k)为组合观测量的电离层延迟影响系数,λ(i, j, k)为组合观测量波长,Nr, (i, j, k)为组合观测量的整周模糊度,υr, (i, j, k)为载波相位观测噪声,er, (m, n, l)为伪距观测噪声。
两式相减并作站间单差可消除卫星钟差、对流层误差等与频率无关的误差,得到方程如下:
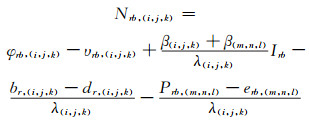
|
(3) |
在相邻历元间求差可消除硬件时延项,忽略历元间多路径延迟变化项,可得周跳估值为(后面公式中将省略站间单差标记rb):
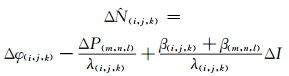
|
(4) |
则周跳探测条件为:

|
(5) |
式中,
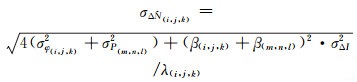
|
(6) |
为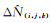
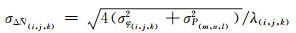
|
(7) |
由相位组合观测量周跳估值直接取整获得正确周跳值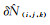

|
(8) |
为了探测并修复3个原始频点上的周跳值,需要3个组合系数线性无关的伪距相位组合。根据Feng[12]和Cocard等[13]提出的三频最优组合观测量的选取标准,可以确定两个最优超宽巷组合(0, -1, 1)、(1, 4, -5),因此需要确定第3个伪距相位组合。李金龙[14]研究指出,组合系数之和越小,电离层对超宽巷或宽巷组合的噪声影响越小。表 1列出所有组合系数之和不为0且小于2的组合观测量系数,比较了忽略与考虑电离层延迟影响两种情况下周跳估值标准差的大小。根据北斗三频观测值特点,假设北斗3个频点伪距与相位观测值为等精度独立观测值,观测噪声标准差分别为σP1=σP2=σP3=0.3 m和σφ1=σφ2=σφ3=0.003 m,经站间单差及历元间单差(以下简称双差)后电离层延迟的误差噪声标准差为σδI=0.02 m。
|
|
表 1 组合系数之和小于2的超(宽)巷组合 Tab. 1 EWL(WL)combination (the sum of combination coefficient less than 2) |
由表 1可见,无论是忽略还是考虑双差电离层延迟影响,超宽巷组合(4, -2, -3)的周跳估值标准差均是最小,因此选用(0, -1, 1)、(1, 4, -5)、(4, -2, -3)3个线性无关的组合观测量进行周跳的探测与修复。表 2给出了这3个组合的周跳估值标准差及其取整成功率,可以看出,在忽略电离层延迟的影响下,3个组合的取整成功率均很高,但考虑电离层影响的情况下,组合(4, -2, -3)会受到影响。
|
|
表 2 所选组合周跳估值标准差及取整成功率 Tab. 2 Standard deviation and bootstrapping success rate of the selected combinations |
分别选取350 m及72 km两种长度的基线进行实验分析(表 3)。
|
|
表 3 BDS实验数据概述 Tab. 3 Overview of BDS data |
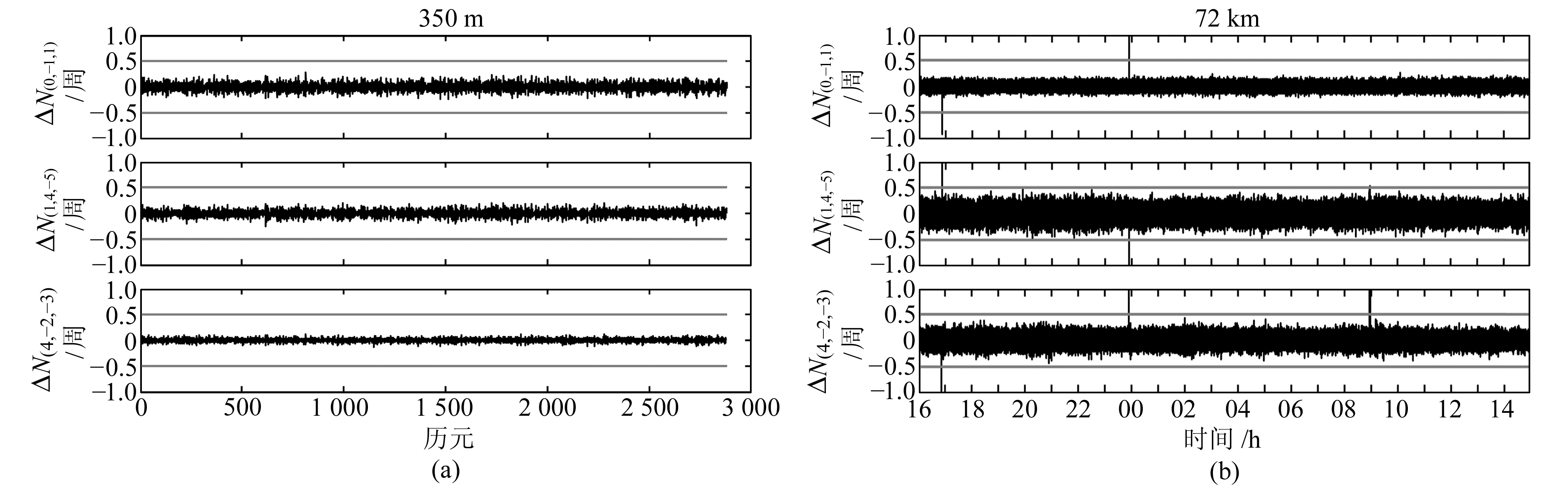
图 1给出两种基线下三频伪距相位组合的周跳探测量序列。对于中长基线72 km,因原始观测数据中存在周跳值,在图 1(b)的估值序列中可以看到3个跳变值,在进行后续实验分析时只要剔除这3个周跳值的影响,就不会影响实验结论。以下不再赘述。
|
图 1 三频伪距相位组合周跳探测量序列 Fig. 1 Estimation of the triple-frequency code-phase cycle slip detect values |
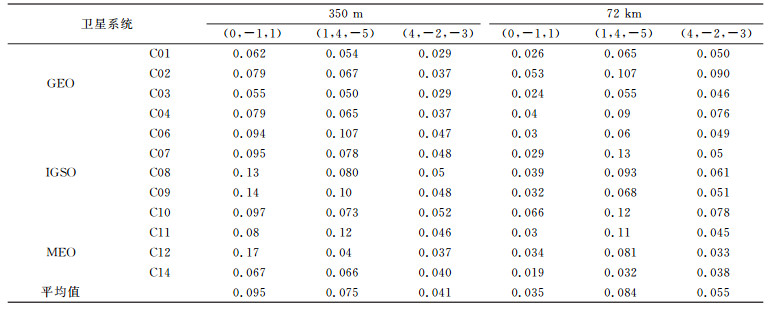
由图 1可见,无论是短基线还是中长基线,3个周跳探测量的估值序列均在0.5周内,保证了周跳探测的准确率。同时注意到,随着基线增长,组合(1, 4, -5)、(4, -2, -3)估值序列噪声会变大。表 4(单位:周)列出了3个组合周跳估值序列的标准差(STD),3个伪距相位组合探测量的标准差均较小,大部分小于0.1周;组合(4, -2, -3)表现良好,甚至优于组合(1, 4, -5)。随着基线长度的增加,组合(1, 4, -5)、(4, -3, -2)由于受噪声以及电离层延迟的影响,变化幅度较大,但其变化范围能够稳定在0.2周之内,仍可以有效准确地确定组合周跳整数估值。
|
|
表 4 三频伪距相位组合探测量的STD值 Tab. 4 STD of the triple-frequency code-phase cycle slip detect values |
为了验证选取的3个三频伪距相位组合的周跳探测效果,选择在350 m和72 km的两条基线不同历元的3个原始频点上分别加上1周的小周跳(表 5)。
|
|
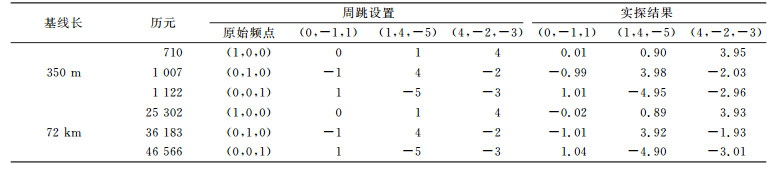
表 5 设置周跳及实探结果 Tab. 5 Results of simulated cycle slip |
在表 5最后3列及图 2中给出了设计周跳的实探结果。可以看出,对于3个原始频点上,即使1周的小周跳,利用3个三频伪距相位组合(0, -1, 1)、(1, 4, -5)及(4, -2, -3)也可以准确探测出。

|
图 2 三频伪距相位周跳探测结果 Fig. 2 Results of triple-frequency code-phase cycle slip detect |
通过大量的实验发现,随着基线长度的增加,受残留电离层影响,组合(1, 4, -5)及(4, -2, -3)周跳估值序列的噪声变大,在某些历元上可能会出现1周小周跳的误探情况,将给周跳的探测与修复带来困难。例如,在某一历元中如果只有组合(1, 4, -5)发生了1周的小周跳,有时无法判断其是真实周跳还是误探,因此需进一步改善三频伪距相位组合周跳探测与修复算法。
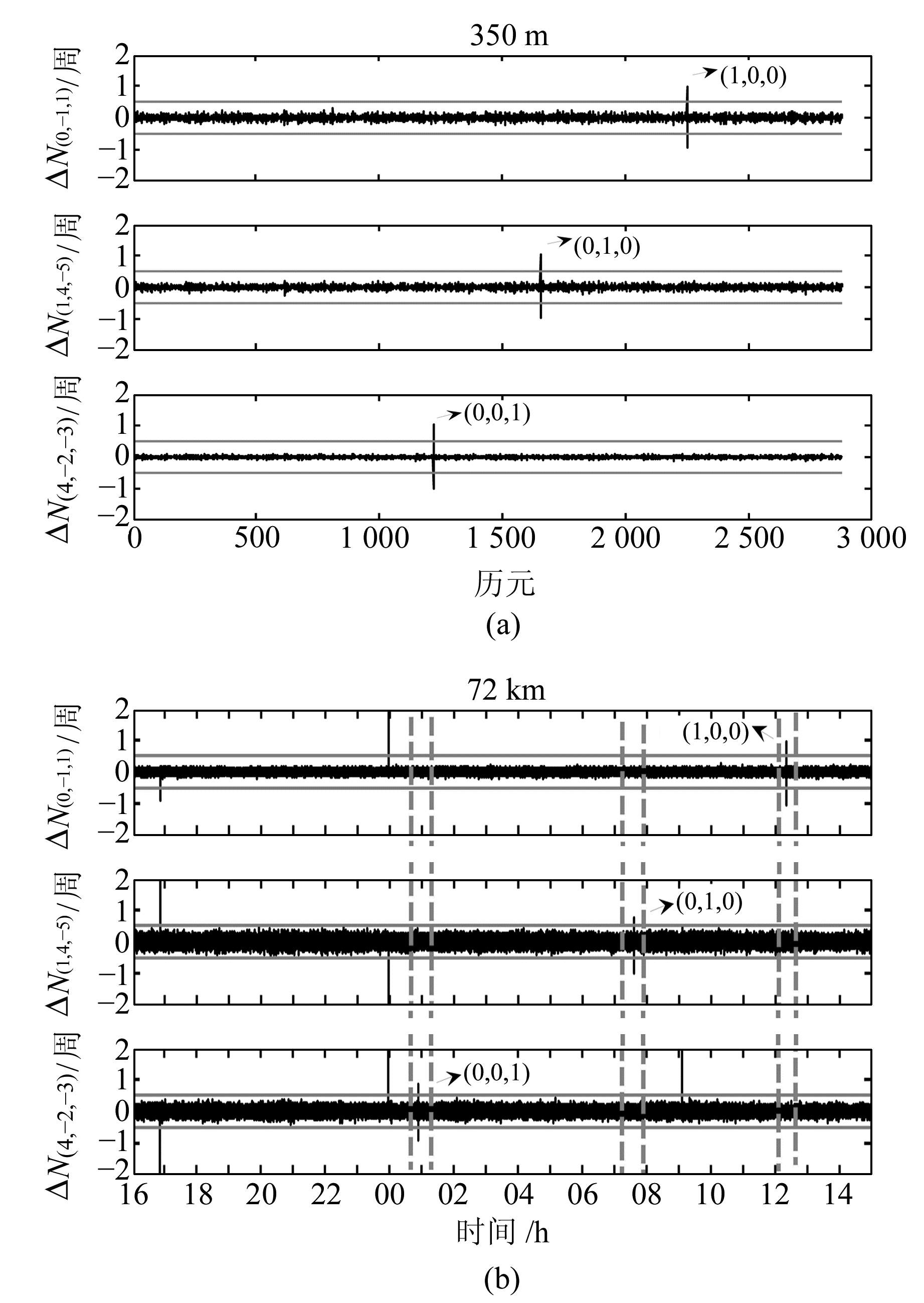
图 3模拟了三频伪距相位组合(0, -1, 1)、(1, 4, -5)及(4, -2, -3)周跳误探情况,即分别在350 m基线的1 252历元、1 650历元、2 302历元以及72 km的33 162历元、58 210历元、78 235历元上模拟了1周的小周跳(大部分实验中对于1周的小周跳无法判断是真实周跳还是误探情况)。表 6(单位:周)列出了组合(0, -1, 1)、(1, 4, -5)及(4, -2, -3)出现1周的误探情况时对3个频点上周跳探测值所产生的影响,例如组合(1, 4, -5)出现1周的误探,在频点B1上将产生5周的误探。
|
图 3 三频伪距相位组合周跳误探 Fig. 3 Sketch of detecting a wrong slip |
|
|
表 6 组合(0, -1, 1)、(1, 4, -5)及(4, -2, -3)可能出现的误探 Tab. 6 The probability of detecting a wrong slip |
基于以上可能出现的误探情况,提出利用电离层残差法辅助三频伪距相位周跳探测的方法:
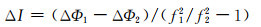
|
(9) |
式中,ΔI为经过站间单差及历元间单差所得双差电离层残差。
当有周跳发生时,ΔI会显著增大,但由于基线长度的增加,ΔI通过双差后不能被完全消除,且可能会有较大的波动幅度,无法判断发生的较大跳变是由于周跳还是电离层残差自身的变化。值得注意的是,前后历元间的电离层残差变化不是很大,因此可将ΔI再在历元间作差:
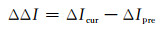
|
(10) |
得到周跳探测条件为:
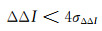
|
(11) |
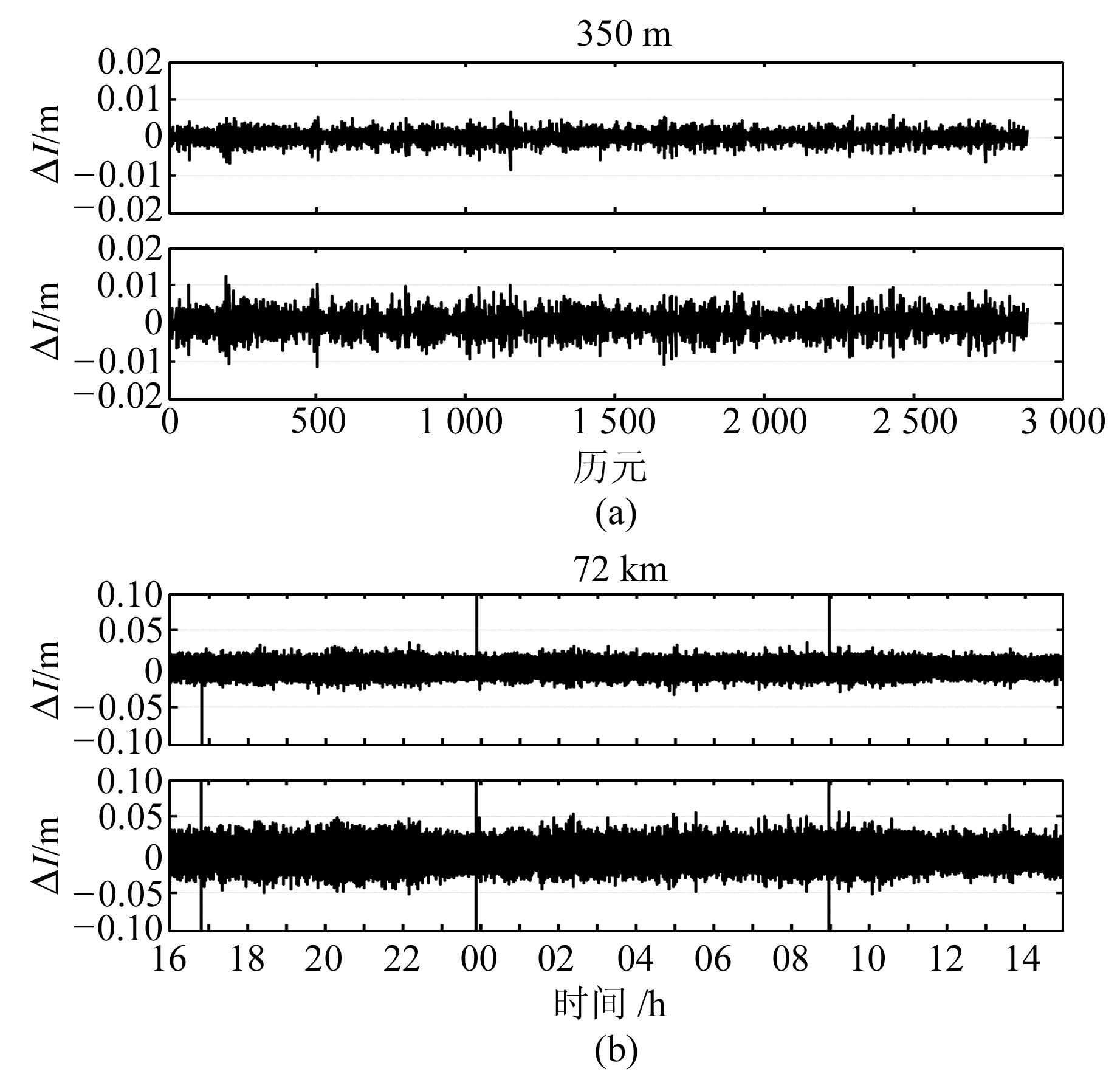
图 4及表 7(单位m)给出了电离层残差及电离层残差的标准差(STD)。可以看出,电离层残差及其历元间作差后具有较小的噪声,无论是短基线还是中长基线,所有卫星的电离层残差的STD值均在1 cm以内,保证了周跳的正确探测。
|
图 4 电离层残差 Fig. 4 The residual ionospheric delay |
|
|
表 7 电离层残差STD值比较 Tab. 7 STD of the residual ionospheric delay |
图 5给出与图 3三频伪距相位组合周跳探测相对应的电离层残差辅助周跳探测实验结果,在利用伪距相位组合(1, 4, -5)或(4, -2, -3)无法判断是真实周跳还是电离层干扰的情况下,利用电离层残差辅助探测法可以进一步辅助判定。当三频伪距相位组合周跳探测法与电离层残差辅助法同时探测到某一历元上有周跳发生时,认为此时在该历元上发生了周跳,否则是误探。值得注意的是,电离层残差法对于组合(0, -1, 1)上发生的1周小周跳不敏感,但由于组合(0, -1, 1)周跳估值取整成功率非常高,几乎为100%,不会出现误探情况,因此电离层残差辅助法主要是用来针对组合(1, 4, -5)或(4, -2, -3)可能出现的误探情况。

|
图 5 电离层残差辅助周跳探测实验 Fig. 5 Results of the cycle slip with the ionospheric residual error method |
本文针对北斗不同长度基线下的周跳探测与修复展开研究,首先以周跳估值噪声标准差为选取标准,优选了组合(4, -2, -3),并与两个确定的超宽巷组合(0, -1, 1)、(1, 4, -5)构成3个线性无关的伪距相位组合进行周跳探测与修复,并模拟周跳实验,在原始频点上各加上1周周跳。结果表明,优选的3个伪距载波组合能够成功探测到1周的小周跳;针对三频伪距相位组合可能出现误探的情况,采用电离层残差辅助三频伪距相位组合周跳探测,两种方法结合可以成功准确地探测出所有大小的周跳。
| [1] |
Yang Y X. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Science Bulletin, 2011, 56(26): 2813-2819 DOI:10.1007/s11434-011-4627-4
(  0) 0) |
| [2] |
范建军, 王飞雪, 郭桂蓉. GPS三频非差观测数据周跳的自动探测与改正研究[J]. 测绘科学, 2006, 31(5): 24-26 (Fan Jianjun, Wang Feixue, Guo Guirong. Auotomated Cycle Slip Detection and Correction for GPS Triple-Frequency Undifferenced Observations[J]. Science of Surveying and Mapping, 2006, 31(5): 24-26 DOI:10.3771/j.issn.1009-2307.2006.05.006)
(  0) 0) |
| [3] |
董丽娜, 袁运斌, 王海涛, 等. 一种GPS三频非差周跳探测相位组合的优选方法研究[J]. 大地测量与地球动力学, 2012, 32(3): 106-110 (Dong Li'na, Yuan Yunbin, Wang Haitao, et al. On an Optimum Selection Method of GPS Triple-Frequency Phase Combination Applied to Undifferenced Cycle Slip Detection[J]. Journal of Geodesy and Geodynamics, 2012, 32(3): 106-110)
(  0) 0) |
| [4] |
熊伟. 多频数据组合在周跳探测和修复上的应用[J]. 武汉大学学报:信息科学版, 2007, 32(4): 319-322 (Xiong Wei. Application of Multi-Frequency Combination Observation in Cycle Slip Detection and Restoration[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 319-322)
(  0) 0) |
| [5] |
Lacy M C D, Reguzzoni M, Sansò F, et al. Real-Time Cycle Slip Detection in Triple-Frequency GNSS[J]. GPS Solutions, 2012, 16(3): 353-362 DOI:10.1007/s10291-011-0237-5
(  0) 0) |
| [6] |
Dai Z, Knedlik S, Loffeld O. Real-Time Cycle-Slip Detection and Determination for Multiple[C]. The 5th Workshop on Positioning, Navigation and Communication, Hannover, 2008
(  0) 0) |
| [7] |
伍岳, 黄学斌, 程温鸣, 等.多频数据在原始载波观测值预处理中的应用[C].中国全球定位系统技术应用协会第8次年会, 北京, 2005 (Wu Yue, Huang Xuebin, Cheng Wenming, et al. Application of Multi-Frequency Data in the Process of Original Carrier Observations[C]. The 8th Annual Conference of China Association for Global Positioning System(GPS) Technolog, Beijing, 2005)
(  0) 0) |
| [8] |
李金龙. GNSS三频精密定位数据处理方法研究[D].郑州: 信息工程大学, 2011 (Li Jinlong. Researches on the Algorithms of GNSS Three Frequency Precise Positioning[D]. Zhengzhou: Information Engineering University, 2011)
(  0) 0) |
| [9] |
谢凯, 柴洪洲, 王敏. 不同采样间隔下的三频周跳探测与修复算法研究[J]. 大地测量学与地球动力学, 2014, 34(1): 139-143 (Xie Kai, Chai Hongzhou, Wang Min. Cycle Slip Detection and Repair with Different Sampling Interval Based on Compass Triple-Frequency[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 139-143)
(  0) 0) |
| [10] |
黄令勇, 宋力杰, 王琰, 等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5): 763-768 (Huang Lingyong, Song Lijie, Wang Yan, et al. Beidou Triple-Frequency Geometry-Free Phase Combination for Cycle-Slip Detection and Correction[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 763-768)
(  0) 0) |
| [11] |
李博峰.混合整数GNSS函数模型及随机模型参数估计理论与方法[D].上海: 同济大学, 2010 (Li Bofeng. Theory and Method of Parameter Estimation in Mixed Integer GNSS Model[D]. Shanghai: Tongji University, 2010)
(  0) 0) |
| [12] |
Feng Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862 DOI:10.1007/s00190-008-0209-x
(  0) 0) |
| [13] |
Cocard M, Bourgon S, Kamali O, et al. A Systematic Investigation of Optimal Carrier-Phase Combinations for Modernized Triple-Frequency GPS[J]. Journal of Geodesy, 2008, 82(9): 555-564 DOI:10.1007/s00190-007-0201-x
(  0) 0) |
| [14] |
李金龙.北斗/GPS多频实时精密定位理论与算法[D].郑州: 信息工程大学, 2014 (Li Jinlong.BDS/GPS Multi-Frequency Real-Time Kinematic Positioning Theory and Algorithms [D].Zhengzhou: Information Engineering University, 2014)
(  0) 0) |
2. 78125 Troops of PLA, Chengdu 610066, China
 2017, Vol. 37
2017, Vol. 37