2. 现代工程测量国家测绘地理信息局重点实验室, 上海市四平路1239号, 200092
地基GPS反演可降水量是GPS气象学中的重要方法[1]。为了获取高精度的可降水量,地面气象数据必不可少。但实际工作中,由于操作失误、仪器失灵等原因会造成部分时段气象数据缺失。因而,在气象数据缺失时如何通过地基GPS反演可降水量是一项十分重要的工作。王勇等[2]在气象数据缺失时,推导了由GPS对流层延迟直接推算可降水量的模型;常亮等[3]利用NCEP/NCAR全球再分析资料估算可降水量,但获得的数据时间分辨率较低;穆宝胜[4]利用GAMIT中的模型估计气象数据,从而获得气象数据缺失时的可降水量。但以上研究较为单一,没有对不同的方法进行比较。
本文选取两类插值对象、GAMIT生成Z文件共3种方案,将缺失数据分为长、短时段,分别计算气象数据缺失时的可降水量,试图选取不同情况下合适的、具有高时间分辨率的反演方法。
1 可降水量计算方法 1.1 插值方法选用三次样条插值和奇异谱分析迭代插值方法,对缺失的气象数据进行插值。奇异谱分析迭代插值方法[5]是一种数据驱动、自适应的方法,且无需预知时间序列的先验信息,能够反映原始数据内部的周期特性。该方法分两个步骤[6]:
1) 循环选取最佳窗口长度L和主成分个数P。将原始数据分为训练数据Xt、交叉验证数据Xc、缺失数据Xl,Xc用于判定所选参数L和P是否为最佳。原始数据除Xc、Xl外的数据为Xt;将Xt去中心化,Xc、Xl赋值0,得到新序列Xn。
选取一组L和P,对Xn进行奇异谱分析得到重构序列Xr。用Xr对应位置的值替换Xc、Xl处的值,得到新序列Xn2。循环进行奇异谱分解与替换的过程,直至Xn2与Xn之差的绝对值的最大值满足限差要求,计算Xc与已知数据的均方根误差。选取一组新的L和P,重复上述过程。选取满足均方根误差最小的一组L0和P0作为最佳参数。
2) 缺失数据插值。将Xl赋值0,其余数据进行去中心化处理,得到Xn3。选取窗口长度L0和主成分个数P0,循环进行奇异谱分解与替换的过程,直至满足限差要求, 此时得到的序列Xn4即为对缺失数据插值后的序列。
1.2 GAMIT生成Z文件方法在GAMIT中,metutil程序可以使用RINEX格式的气象文件或由内部模型估计得到的Z文件计算可降水量。Z文件由model程序计算得到,包括气压、温度、先验天顶干延迟等参数[7]。将sestbl.表中Output met属性改为Y,即可在解算基线的同时生成Z文件。在气象数据缺失时,可以使用Z文件代替气象文件进行可降水量计算,简称为Z文件法。地基GPS反演可降水量的具体原理在文献[8-9]中有详尽叙述,这里不再重复。
2 实验方案 2.1 数据源实验中用于反演可降水量的GPS观测数据由同济大学GPS参考站(TJCH站)获得,气象数据由TJCH站的气象仪获得,微波辐射计数据由与TJCH站并址的微波辐射计获得。由于晴空下微波辐射计数据质量较高[10],可作为真值使用,但在雨天数据质量会下降。因此实验时段选为2015-02-02 02:00~02-14 15:00(共302 h,称为总时段1)和2015-10-09 00:00~10-26 12:00(共421 h,称为总时段2),时段内均无降雨,为连续时段。下文中不同方案提取得到的可降水量时间间隔均为1 h。
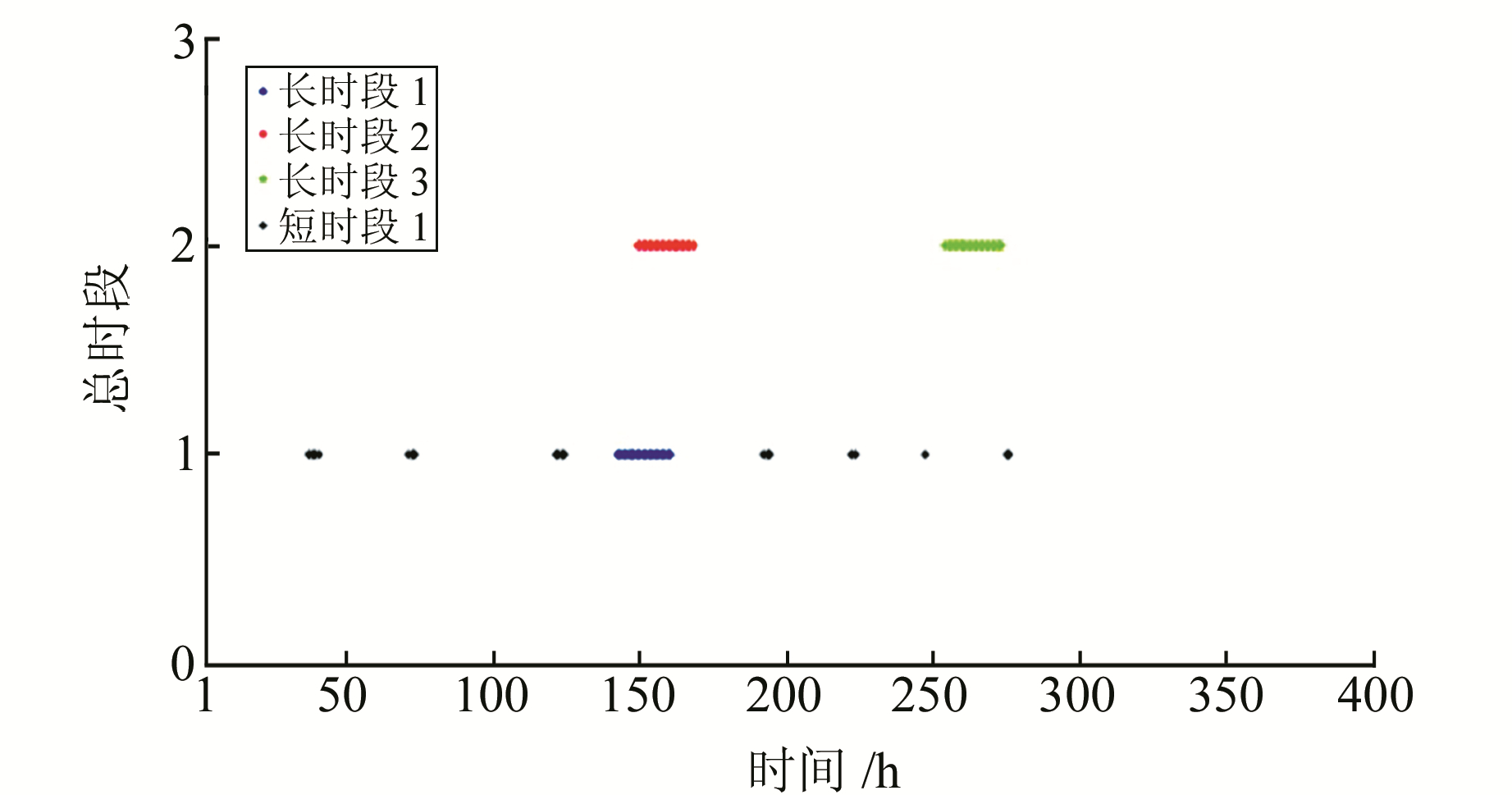
2.2 方案设计假设实验时段中有气象数据缺失,为了更加全面地分析缺失数据时间长短对不同方法计算可降水量的影响,将实验时段分为长时段缺失和短时段缺失两种情况。其中总时段1分为1个19 h的长时段(称为长时段1)数据缺失,以及2个4 h、2个3 h、2个2 h、1个1 h共19 h的短时段(称为短时段1)数据缺失,总时段2分为2个20 h的长时段(称为长时段2、3)数据缺失。缺失分布情况如图 1所示,图中横坐标为总时段内的小时数。
|
图 1 数据缺失分布 Fig. 1 Location of missing data |
因为计算较高精度的可降水量需要用到气象数据,所以在气象数据缺失的时段可降水量也是缺失的。因而将插值对象分为两种:直接对缺失的可降水量数据进行插值;对缺失的气象数据进行插值,再利用插值得到的气象数据计算可降水量。插值方法采用三次样条插值和奇异谱分析迭代插值。
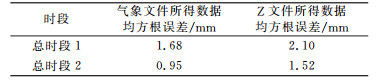
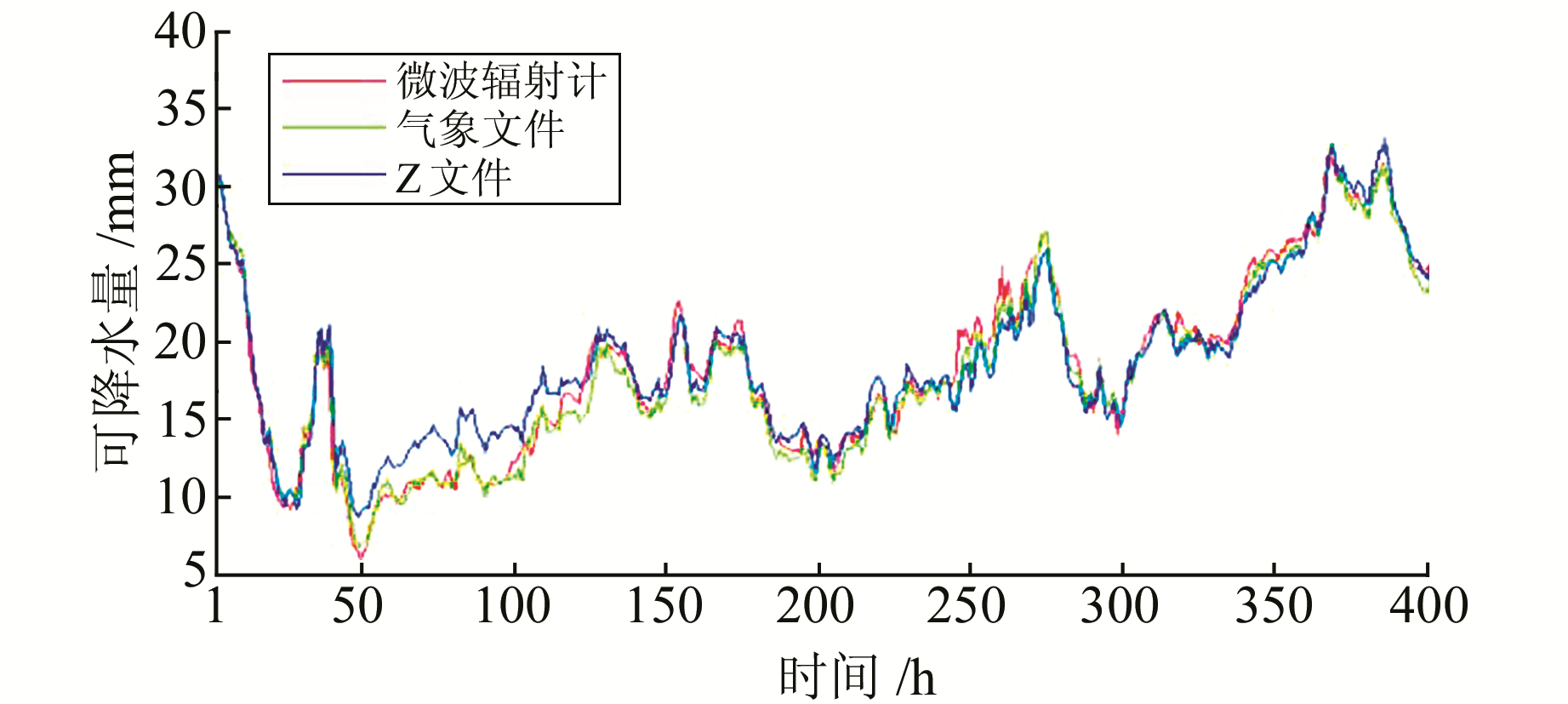
3 实验分析 3.1 Z文件法实验在GAMIT中,利用Z文件法可以得到完整的实验时段可降水量数据,其中总时段1、2分别如图 2、3所示。计算利用气象文件和Z文件得到的完整时段可降水量与微波辐射计数据的均方根误差,得到表 1。可以发现,利用实测气象数据计算得到的可降水量精度优于利用Z文件计算得到的数据。

|
图 2 总时段1 Z文件计算结果 Fig. 2 Results of Z files in total period 1 |
|
图 3 总时段2 Z文件计算结果 Fig. 3 Results of Z files in total period 2 |
|
|
表 1 总时段几种数据间均方根误差 Tab. 1 RMSE between several data in total period |
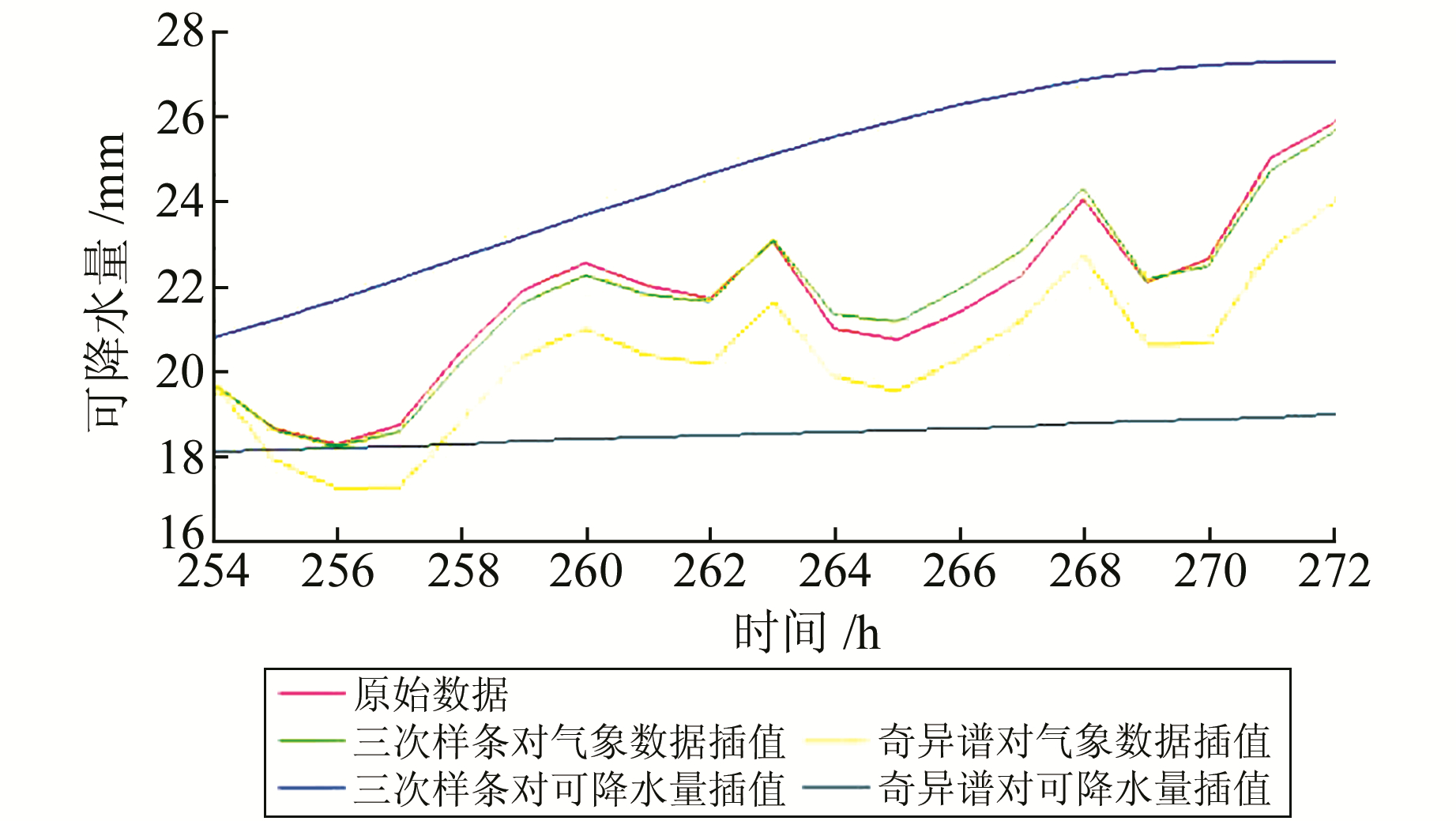
采用三次样条插值和奇异谱分析迭代插值对长时段1、2、3的可降水量数据直接进行插值,得到图 4~6中蓝色和黑色线段;采用三次样条插值和奇异谱分析迭代插值对长时段1、2、3的气象数据进行插值,再利用插值得到的气象数据计算此时的可降水量,得到图 4~6中绿色和黄色线段。红色线段为利用气象仪采集的气象数据计算的可降水量。

|
图 4 长时段1插值结果 Fig. 4 Data interpolation in long period 1 |

|
图 5 长时段2插值结果 Fig. 5 Data interpolation in long period 2 |
|
图 6 长时段3插值结果 Fig. 6 Data interpolation in long period 3 |
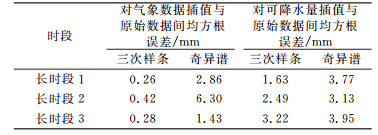
在图 4~6中,三次样条插值能较好地反映原始数据的变化趋势,但对可降水量的插值结果较为平缓,无法反映数据变化;而奇异谱迭代插值的结果与原始数据相差较大,其效果不如样条插值。分别计算长时段内几种数据与原始数据(由气象文件计算的可降水量)间的均方根误差,见表 2。
|
|
表 2 长时段几种数据间均方根误差 Tab. 2 RMSE between several data in long period |
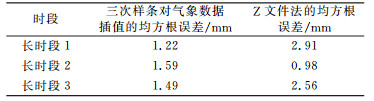
由表 2可知,对气象数据进行插值再计算可降水量的方法的精度优于直接对可降水量插值,而且采用三次样条插值对气象数据插值与实测气象数据间均方根误差最小。该方法能够在一定程度上反映原始数据的变化趋势,在长时段该对原始数据的插值效果最好。分别计算3个长时段内该方法所得数据和Z文件法所得数据与微波辐射计数据间的均方根误差,见表 3。
|
|
表 3 长时段几种数据间均方根误差 Tab. 3 RMSE between several data in long period |
由表 3可知,在长时段1、3中,三次样条对气象数据插值的方法精度较高,而长时段2中Z文件法精度较高。总地来说,三次样条对气象数据插值的方法精度优于Z文件法,在长时段气象数据缺失情况下,可以用该方法计算可降水量。
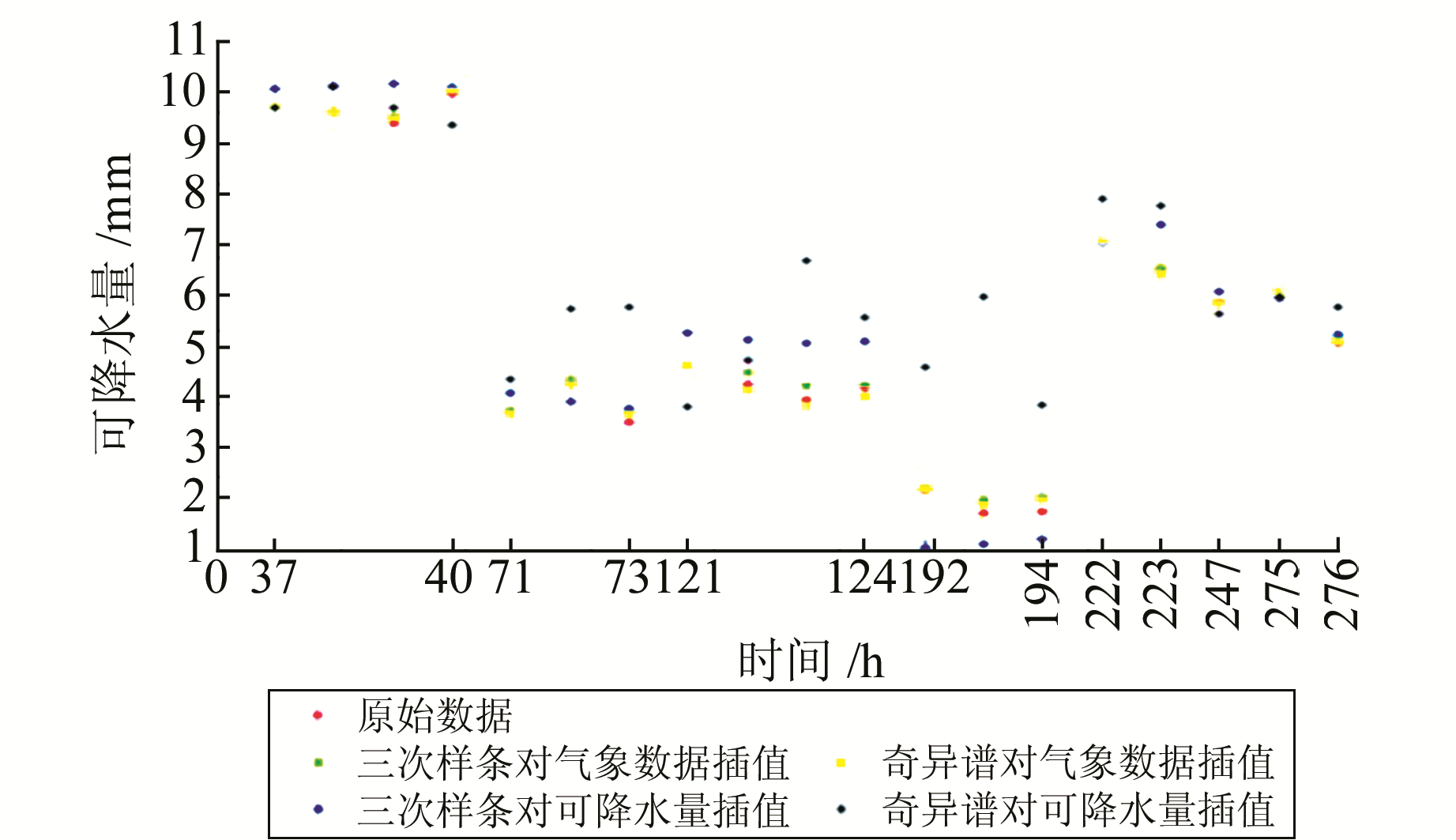
3.3 短时段实验在总时段1中选取37~40 h、71~73 h、121~124 h、192~194 h、222~223 h、247 h、275~276 h共7个短时段,采用与上节同样的方法进行实验。因为每个时段较短,采用散点图表示不同方法所得数据(图 7)。
|
图 7 短时段插值结果 Fig. 7 Data interpolation in short period |
计算短时段内几种不同数据间的均方根误差,见表 3和表 4。由表 4可知,两种插值方法在短时段内的插值效果优于长时段。与长时段相同,采用对气象数据插值的方法效果优于对可降水量直接插值。采用奇异谱迭代插值对气象数据插值的方法与由实测气象文件所得数据间均方根误差最小。分别计算得到短时段内该方法所得数据和Z文件法所得数据与微波辐射计数据间的均方根误差为1.75 mm和2.04 mm。因此,该方法计算结果精度优于Z文件法,在短时段气象数据缺失的情况下,可以采用奇异谱迭代插值对气象数据插值计算可降水量。
|
|
表 4 短时段几种数据间均方根误差 Tab. 4 RMSE between several data in short period |
在气象数据缺失时进行地基GPS反演可降水量,无论长、短时段,对气象数据插值再计算可降水量的方法精度优于直接对可降水量数据插值。在长时段,可以采用三次样条对气象数据插值方法计算可降水量;在短时段,可以采用奇异谱迭代对气象数据插值方法计算可降水量。而利用GAMIT内部模型生成Z文件计算可降水量的方法精度在2 mm左右,虽然不如对气象数据插值再计算可降水量的方法,但当缺失数据占总数据比例较大,通过已知数据不足以进行插值或插值效果较差时,可以考虑采用Z文件法。
| [1] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [2] |
王勇, 刘严萍, 柳林涛, 等. 无气象要素的GPS对流层延迟推算可降水量的研究[J]. 测绘科学, 2007, 32(3): 122-124 (Wang Yong, Liu Yanping, Liu Lintao, et al. The Study of Calculating Precipitable Water Vapor Using GPS Zenith Tropospheric Delay without Meteorological Data[J]. Science of Surveying and Mapping, 2007, 32(3): 122-124 DOI:10.3771/j.issn.1009-2307.2007.03.048)
(  0) 0) |
| [3] |
常亮, 何秀凤. 综合GPS和NCEP在区域降水预报中的应用研究[J]. 中国科学:物理学力学天文学, 2010, 40(5): 685-692 (Chang Liang, He Xiufeng. Regional Precipitation Forecast Using GPS and NCEP[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2010, 40(5): 685-692)
(  0) 0) |
| [4] |
穆宝胜.地基GPS反演大气可降水量在昆明地区的应用研究[D].昆明: 昆明理工大学, 2013 (Mu Baosheng. Ground-based GPS Inversion of the Applied Research of Atmospheric Precipitation in Kunming Area[D]. Kunming: Kunming University of Science and Technology, 2013)
(  0) 0) |
| [5] |
Kondrashov D, Ghil M. Spatio-Temporal Filling of Missing Points in Geophysical Data Sets[J]. Nonlinear Processes in Geophysics, 2006, 13(2): 151-159 DOI:10.5194/npg-13-151-2006
(  0) 0) |
| [6] |
王辉赞, 张韧, 刘巍, 等. 奇异谱迭代插补的改进算法及其在缺损数据恢复中的应用[J]. 应用数学和力学, 2008, 29(10): 1227-1236 (Wang Huizan, Zhang Ren, Liu Wei, et al. Improved Interpolation Method Based on Singular Spectrum Analysis Iteration and Its Application in Missing Data Recovery[J]. Applied Mathematics and Mechanics, 2008, 29(10): 1227-1236 DOI:10.3879/j.issn.1000-0887.2008.10.010)
(  0) 0) |
| [7] |
Department of Earth and Planetary Sciences, MIT. Document for GAMIT GPS Analysis Software[Z].Cambridge: MIT, 2010
(  0) 0) |
| [8] |
李国平.地基GPS遥感大气可降水量及其在气象中的应用研究[D].成都: 西南交通大学, 2007 (Li Guoping. On the Remote Sensing of Precipitable Water Vapor Using Ground-based GPS Technique and Applications in Meteorology[D].Chengdu: Southwest Jiaotong University, 2007)
(  0) 0) |
| [9] |
王勇, 柳林涛, 梁洪有, 等. 基于GPS技术的高原与平原地区可降水量的研究[J]. 大地测量与地球动力学, 2006, 26(1): 88-91 (Wang Yong, Liu Lintao, Liang Hongyou, et al. Research on Precipitable Water Vapor in Plateau and Plain Areas with GPS Technique[J]. Journal of Geodesy and Geodynamics, 2006, 26(1): 88-91)
(  0) 0) |
| [10] |
毕研盟, 毛节泰, 刘晓阳, 等. 应用地基GPS遥感倾斜路径方向大气水汽总量[J]. 地球物理学报, 2006, 49(2): 335-342 (Bi Yanmeng, Mao Jietai, Liu Xiaoyang, et al. Remote Sensing of the Amount of Water Vapor along the Slant Path Using the Ground-base GPS[J]. Chinese Journal of Geophysics, 2006, 49(2): 335-342 DOI:10.3321/j.issn:0001-5733.2006.02.005)
(  0) 0) |
2. Key Laboratory of Modern Engineering Survey of NASMG, 1239 Siping Road, Shanghai 200092, China
 2017, Vol. 37
2017, Vol. 37