2. 中国空气动力研究与发展中心高速所,绵阳市二环路南段6号,621000;
3. 中国人民解放军陆军工程大学训练基地,徐州市,221004
磁力勘探是利用地表的磁测数据来评估地下未知磁异常体的轮廓形态[1]。在传统反演方法中,常假设总磁化方向与感应磁化方向是一致的。然而,大多数情况下,由于剩余磁化的存在,导致总的磁化方向产生明显的改变,与感应磁化的方向并不一致[2]。同时,由于地下待求未知参数远远多于观测数据点数[3],会导致线性方程求解的模糊性,难以得到方程最优解。为了降低测量误差,常采用L2或者Tikhonov正则化思想[4-5]。确定正则化参数的主要方法有L(LC)曲线、广义交叉验证(GCV)[6-8],其中LC曲线法计算量较大,需要计算多个正则化参数来确定最优解; GCV方法难以保证在每次迭代过程中都能获得GCV功能矩阵的极小值。
针对上述问题,本文提出基于归一化磁源强度的自适应正则化聚焦反演方法。首先,利用归一化磁源强度数据进行反演,减弱剩余磁化对反演结果的影响;然后,引入深度加权矩阵和最小支撑矩阵,避免由于反演参数多于采集点数而导致的欠定问题,并有效解决核函数随深度增大而快速衰减的问题;最后,根据Morozov偏差原则自适应地确定目标函数在迭代过程中的正则化参数,提高了迭代速度和求解精度。
1 Tikhonov正则化聚焦原理磁测数据正演公式如下:
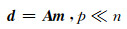
|
(1) |
式中,核函数矩阵A的元素Aij为第i(i=1, 2, 3, …, p)个观测点第j(1, 2, 3, …, n)个单元的响应, 向量d ∈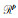
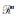
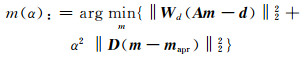
|
(2) |
式中,Wd=diag(1/η1, …, 1/ηp)为数据加权矩阵,ηi为第i个基准噪声的标准偏差,D为正则化矩阵,mapr为模型参数先验信息,α为正则化参数。将式(2)转为如下形式:
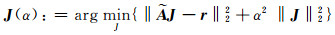
|
(3) |
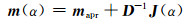
|
(4) |
式中,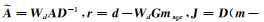
正则化矩阵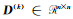
设置迭代过程为:
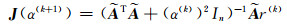
|
(5) |
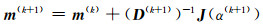
|
(6) |
在求解J(α)时,对矩阵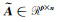
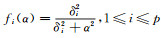
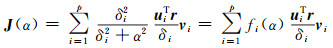
|
(7) |
式中,ui和vi分别为矩阵U和V的第i列。
2.2 归一化磁源强度数据计算磁梯度张量可以由一个二阶矩阵表示:
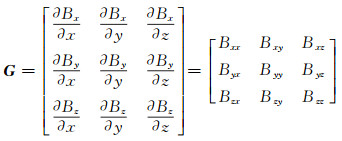
|
(8) |
式中,G为磁梯度张量,Bi(i=x,y,z)为磁场三分量,Bαβ(α、β=x, y, z)为磁梯度张量的9个分量。
归一化磁源强度是由磁偶极子磁梯度张量矩阵推导的旋转不变量,分布于场源中心。假定磁偶极子在观测面(x,y,z)上引起的磁梯度张量矩阵的特征值按单调递减顺序为λ1≥λ2≥λ3,则归一化磁源强度u(x、y、z)可以表示为:
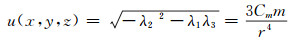
|
(9) |
式中,Cm=10-7H/m,m为磁偶极子磁矩,r为异常源到观测点的距离。由式(9)可见,归一化磁源强度与距离的四次方成反比,与磁矩成正比。
2.3 基于Morozov偏差原则的自适应正则化参数选择徐新禹等[9]讨论了在Tikhonov正则化方法中如何有效选择正则化参数。Zhdanov等[10]提出一种自适应正则化参数的选择方法,定义α(k)=α(1)q(k),q为衰减因子。但是这种方法不能保证每次迭代得到的正则化参数为最佳解,影响求解精度。本文提出基于Morozov偏差原则(MDP)的正则化参数选择方法。
Mead[11]指出,MDP是基于后验策略的偏差原理,利用先验误差信息,使得实测数据与预测数据的残差为最小值的正则化参数即为最优正则化参数。MDP遵循自由度为p-n的卡方分布:
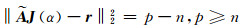
|
(10) |
利用奇异值分解法求解最终的正则化参数:
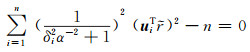
|
(11) |
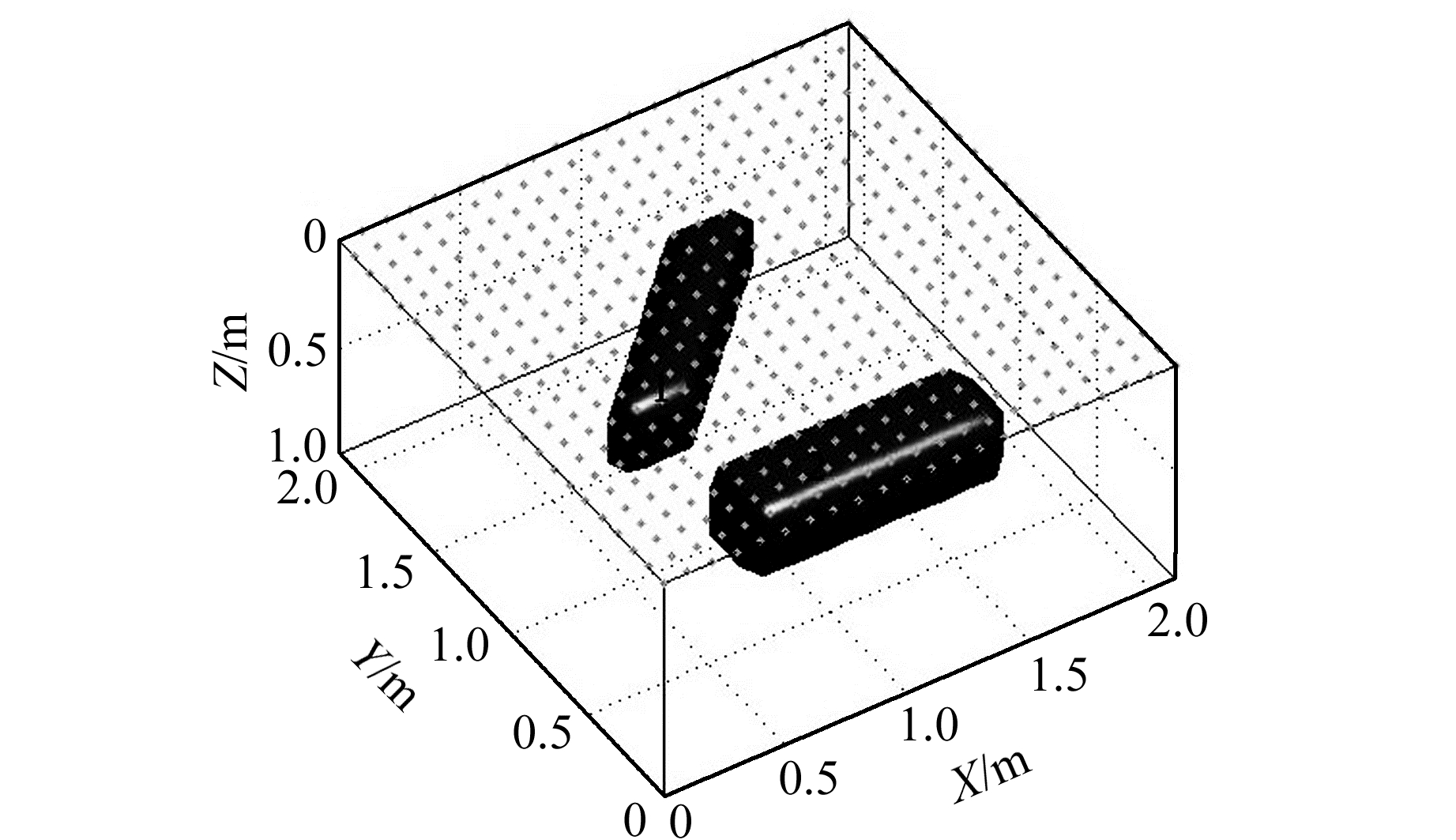
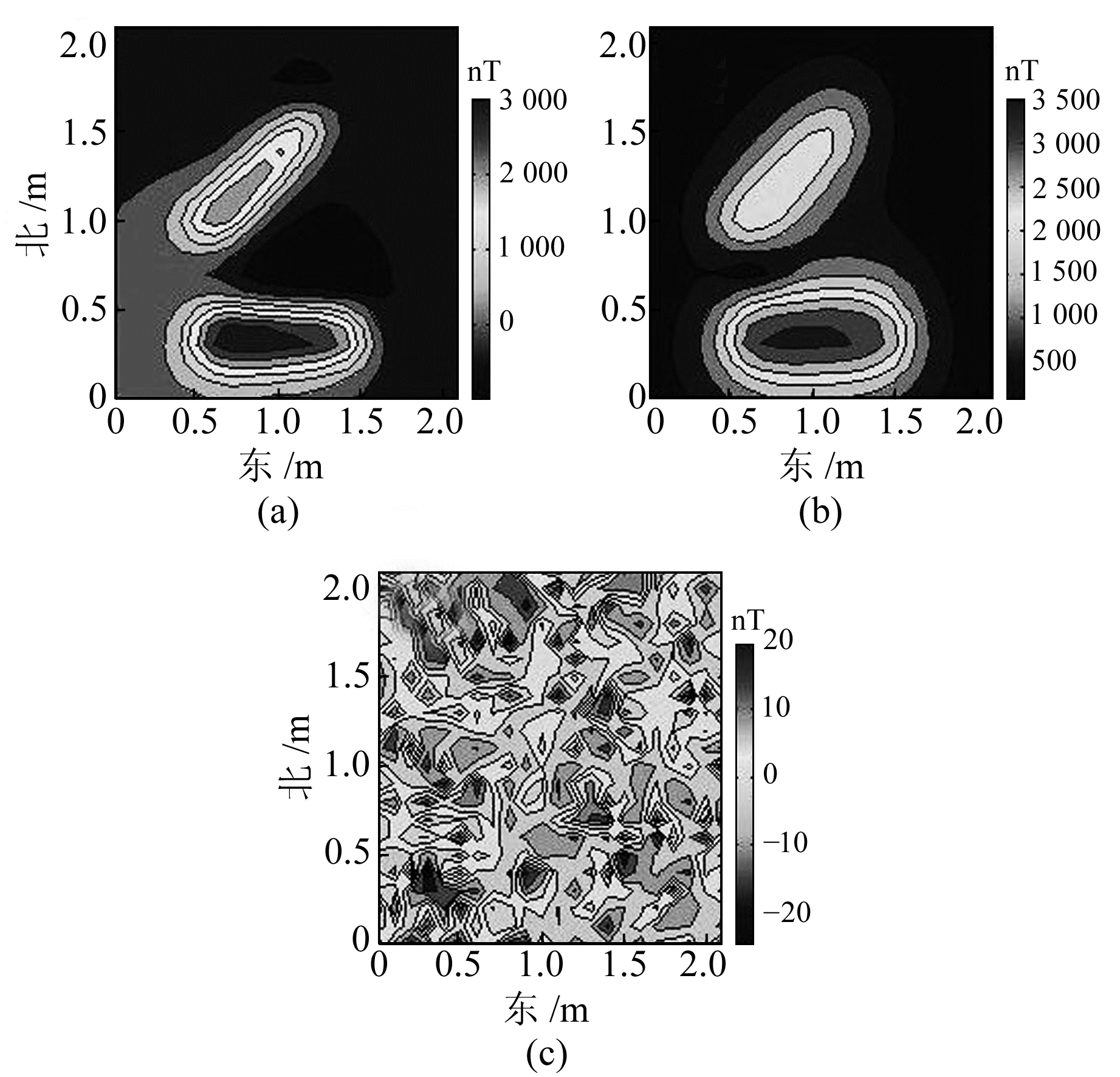
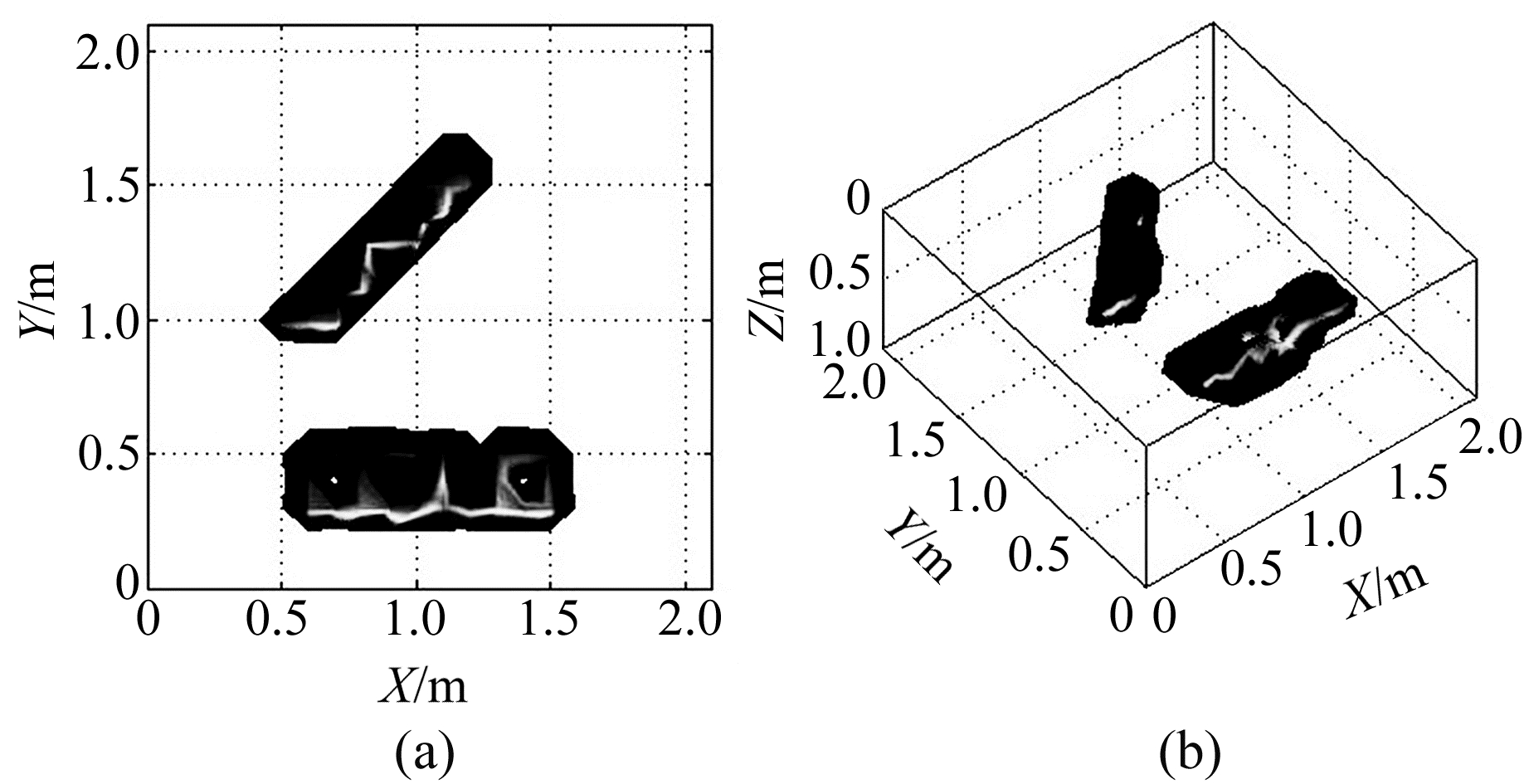
测试模型见图 1,黑色表示待测异常体,其中格点代表观测点矩阵,各部分参数见表 1,其中地磁场倾角为65°,地磁场偏角为-25°。将地下待测空间划分为22×22×10=4 840个单元格,每个单元格均为边长为0.1 m的正方体,地面观测点为22×22=484个网格。反演时,在模型理论归一化磁源强度数据中加入0.03×std(d, 1)×rand(484, 1)的高斯噪声作为实测数据,理论模型正演结果见图 2。可以看出,归一化磁源强度数据与异常体理论模型位置基本重合,进一步论证了归一化磁源强度数据是弱敏感于磁化方向的。反演结果见图 3,可以看出,该方法能够准确还原不同位置、不同形状的模型的轮廓形态,具有较好的横向分辨率。从图 3(b)可以看出,纵向分辨率有所下降,存在一定的边缘效应,这是由于磁总场模量数据仅包含异常体的幅值信息,不包含相位信息。
|
图 1 异常体理论模型 Fig. 1 Theoretical model figure |
|
图 2 磁源强度数据及高斯噪声 Fig. 2 NSS data and Gaussian noise |
|
图 3 反演结果 Fig. 3 Inversion results |
|
|
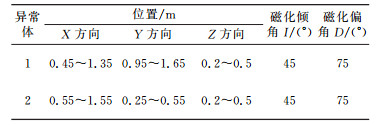
表 1 异常体参数 Tab. 1 Abnormal body parameters |
测试装置为十字形传感器阵列结构,利用Bartington公司的三轴磁通门传感器搭建的磁梯度张量探头,该传感器的分辨率为0.1 nT,实测仪器包括十字形探头、数字采集模块以及软件操作终端。实验中,将探头固定在无磁台架上,在台架的横向和纵向滑道上标注刻度值,通过扫描对实测区域的每一点磁梯度张量值进行测量(图 4)。测区位于石家庄某地,在地理坐标系下,对水平圆柱体铁筒和长方体铁块的组合磁异常进行测试。

|
图 4 实测区域及传感器阵列 Fig. 4 The actual measurement area and sensor array |
长方体铁块位于测区东南方向,中心坐标为(1.5, 0.4, 0.3),尺寸为0.23 m×0.36 m×0.2 m。铁筒位于测区西北方向,中心坐标为(0.6, 1.2, 0.2),圆筒直径为0.1 m,长0.46 m。
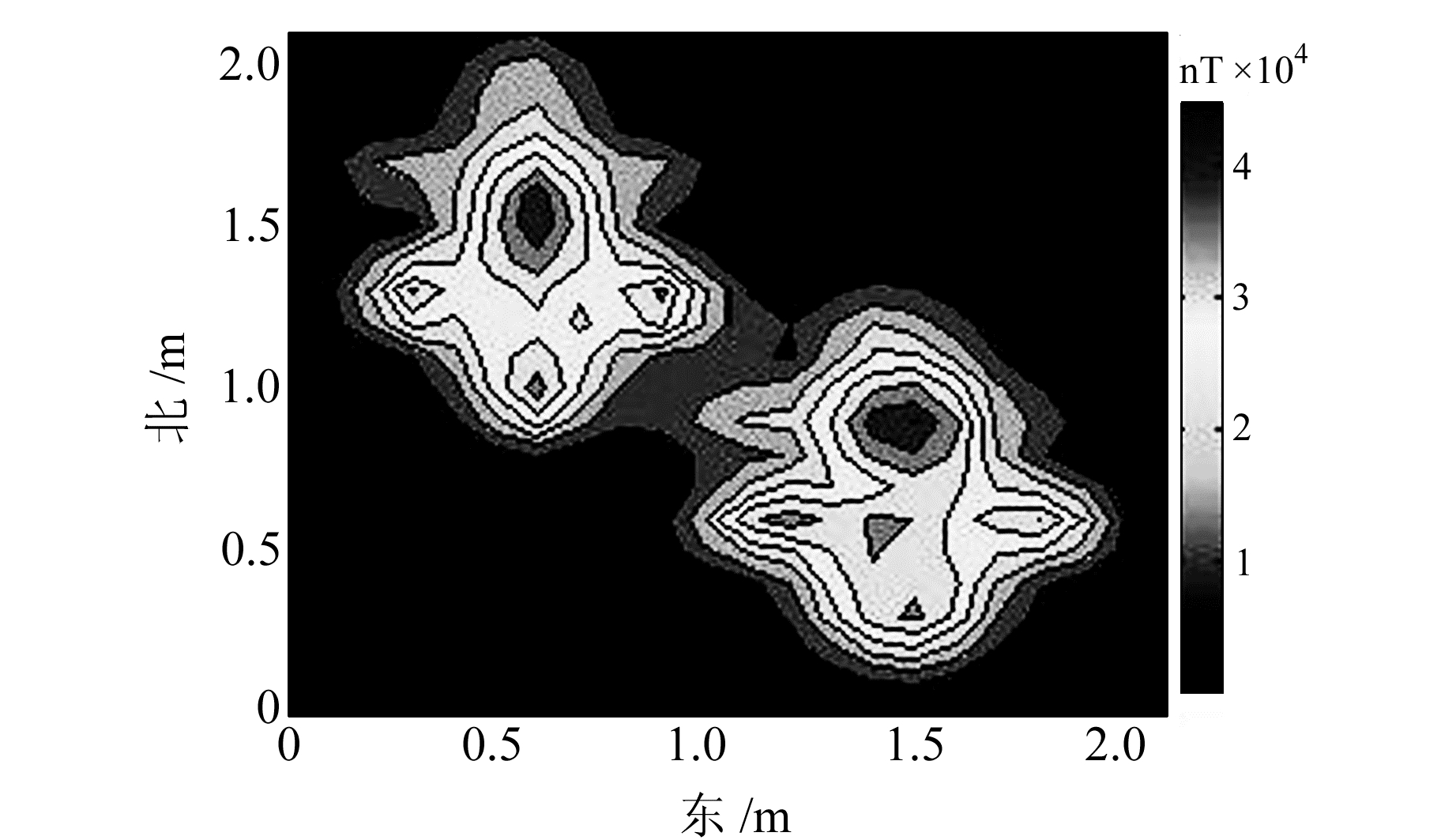
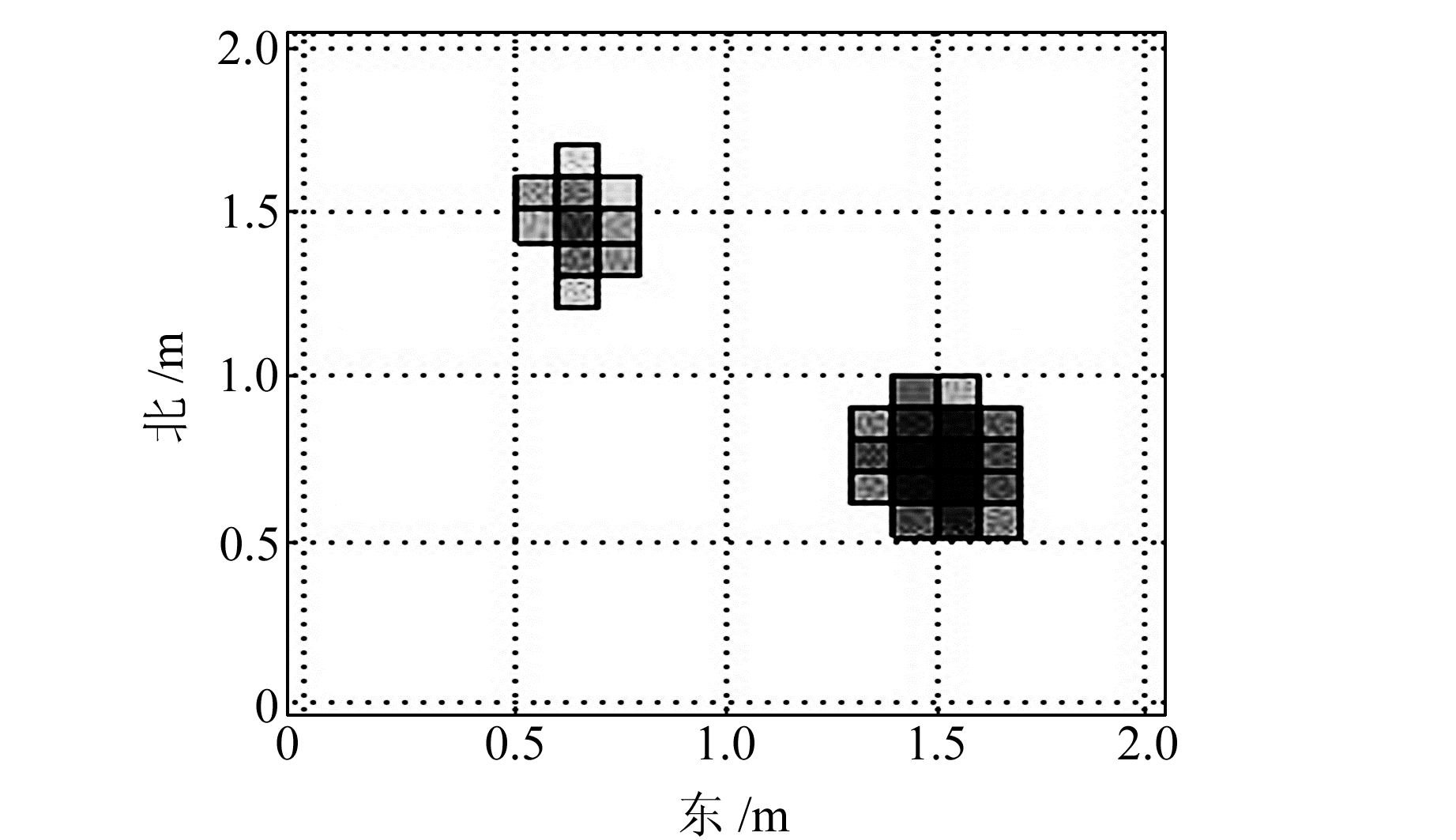
实测数据见图 5。利用归一化磁源强度数据进行反演,获得的三维反演结果见图 6。由反演结果可以看出,本文方法均能很好地重构地下磁性体的轮廓形态,而且反演更加灵活,能够对任意数量的磁性体进行反演。其缺点是在反演过程中损失了相位信息。
|
图 5 归一化磁源强速数据 Fig. 5 Normalized source strength data |
|
图 6 三维反演结果 Fig. 6 3D inversion results |
1) 利用归一化磁源强度数据对磁性目标进行反演,反演结果不受剩余磁化方向的影响,能够很好地校正剩磁效应带来的偏差。
2) 引入深度加权矩阵和最小支撑矩阵对反演模型进行约束,避免了由于反演参数多于采集点数而导致的多解性问题,有效解决了核函数随深度增大而快速衰减的问题。
3) 在迭代过程中,通过奇异值分解法对核函数矩阵进行奇异值分解,利用物性参数上下限函数将反演解转换到合理值域;采用Morozov偏差原则对迭代过程中的正则化参数进行选择,实现了正则化参数的自适应调整。
虽然本文方法能够重构异常体的轮廓形态,但是归一化磁源强度数据仅具有幅值信息,不包含相位信息,反演结果存在一定的边缘效应。
| [1] |
陈召曦, 孟小红, 郭良辉. 重磁数据三维物性反演方法进展[J]. 地球物理学进展, 2012, 27(2): 503-511 (Chen Zhaoxi, Meng Xiaohong, Guo Lianghui. Review of 3D Property Inversion of Gravity and Magnetic Data[J]. Progress in Geophysics, 2012, 27(2): 503-511 DOI:10.6038/j.issn.1004-2903.2012.02.013)
(  0) 0) |
| [2] |
石磊, 孟小红, 郭良辉, 等. 剩磁影响下磁性体磁化方向估计的一种简单算法[J]. 地球物理学进展, 2014, 29(4): 1748-1751 (Shi Lei, Meng Xiaohong, Guo Lianghui, et al. A Simple Algorithm for Estimating the Magnetization Direction of Magnetic Bodies under the Influence of Remanent Magnetization[J]. Progress in Geophysics, 2014, 29(4): 1748-1751)
(  0) 0) |
| [3] |
Boulanger O, Chouteau M. Constraint in 3D Gravity Inversion[J]. Geophysical Prospecting, 2001, 49(2): 265-280 DOI:10.1046/j.1365-2478.2001.00254.x
(  0) 0) |
| [4] |
Tveito A, Langtangen H P, Nielsen B F, et al. Parameter Estimation and Inverse Problems[A]//Elements of Scientific Computing[M]. Berlin Heidelberg: Springer, 2010
(  0) 0) |
| [5] |
Karaoulis M, Revil A, Minsley B, et al. Time-Lapse Gravity Inversion with an Active Time Constraint[J]. Geophysical Journal International, 2013, 196(2): 748-759
(  0) 0) |
| [6] |
Li Y, Oldenburg D W. 3-D Inversion of Magnetic Data[J]. Geophysics, 1996, 61(2): 394-408
(  0) 0) |
| [7] |
Farquharson C G, Oldenburg D W. A Comparison of Automatic Techniques for Estimating the Regularisation Parameter in Non-Linear Inverse Problems[J]. Geophysical Journal International, 2004, 156(3): 411-425 DOI:10.1111/gji.2004.156.issue-3
(  0) 0) |
| [8] |
Vatankhah S, Ardestani V E, Renaut R A. Automatic Estimation of the Regularization Parameter in 2-D Focusing Gravity Inversion: An Application to the Safo Manganese Mine in Northwest of Iran[J]. Journal of Geophysics & Engineering, 2014, 11(4)
(  0) 0) |
| [9] |
徐新禹, 李建成, 王正涛, 等. Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J]. 测绘学报, 2010, 39(5): 465-470 (Xu Xinyu, Li Jiancheng, Wang Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Msission[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 465-470)
(  0) 0) |
| [10] |
Zhdanov M S, Tartaras E. Three-Dimensional Inversion of Multitransmitter Electromagnetic Data Based on the Localized Quasi-Linear Approximation[J]. Geophysical Journal International, 2002, 148(3): 506-519 DOI:10.1046/j.1365-246x.2002.01591.x
(  0) 0) |
| [11] |
Mead J L. Discontinuous Parameter Estimates with Least Squares Estimators[J]. Applied Mathematics & Computation, 2013, 219(10): 5210-5223
(  0) 0) |
2. High Speed Institute, Aerodynamic Research and Development Center, 6 South-Erhuan Road, Mianyang 621000, China;
3. Training Base, Army Engineering University, Xuzhou 221004, China
 2017, Vol. 37
2017, Vol. 37