2. 北京国研数通软件技术有限公司,北京市朝内大街298号,100010
由于地球不可入性等问题的存在[1],很难直接获取地壳内部的结构信息,而是往往利用一些监测手段进行间接反演。正演是反演的基础[2],只有在明确已知断层所产生重力异常现象的前提下,才能根据重力异常测量结果,通过与正演结果的比对,完成断层信息的反演。倾斜台阶可近似表示地层的超覆、倾斜的接触带及倾斜断裂等,因此开展倾斜台阶的相关研究工作具有现实意义。本文所开展的二维倾斜断层的重力异常正演研究工作遵循倾斜台阶正演的数学原理。倾斜断层重力异常正演表达式的推导可追溯至上个世纪四十年代[3],其后国内外学者不断对其进行丰富和完善,其中二维倾斜断层沿剖面方向的正演表达式概括有两种[4-5]。其推导结果很好地修正了在某种特定情况下出现重力异常,导致计算结果畸变(图 1)的问题,给出了畸变发生的条件,形式上虽有不同,但本质相同。然而两者推导的前提条件是沿横坐标正方向倾斜断层延伸至无穷远处,这显然与实际情况不符。本文在前人研究的基础上,将倾斜断层沿横坐标正方向的延伸距离限定在某一固定常数K上,进而推导出了有限长度的二维倾斜断层重力异常正演表达式。其推导前提虽仍然与自然界中真实断层情况存在差异(表达式推导的前提是假定倾斜断层是密度均匀的二度地质体),但与无限延伸的重力异常正演表达式相比,本文推导结果显然更符合实际情况。
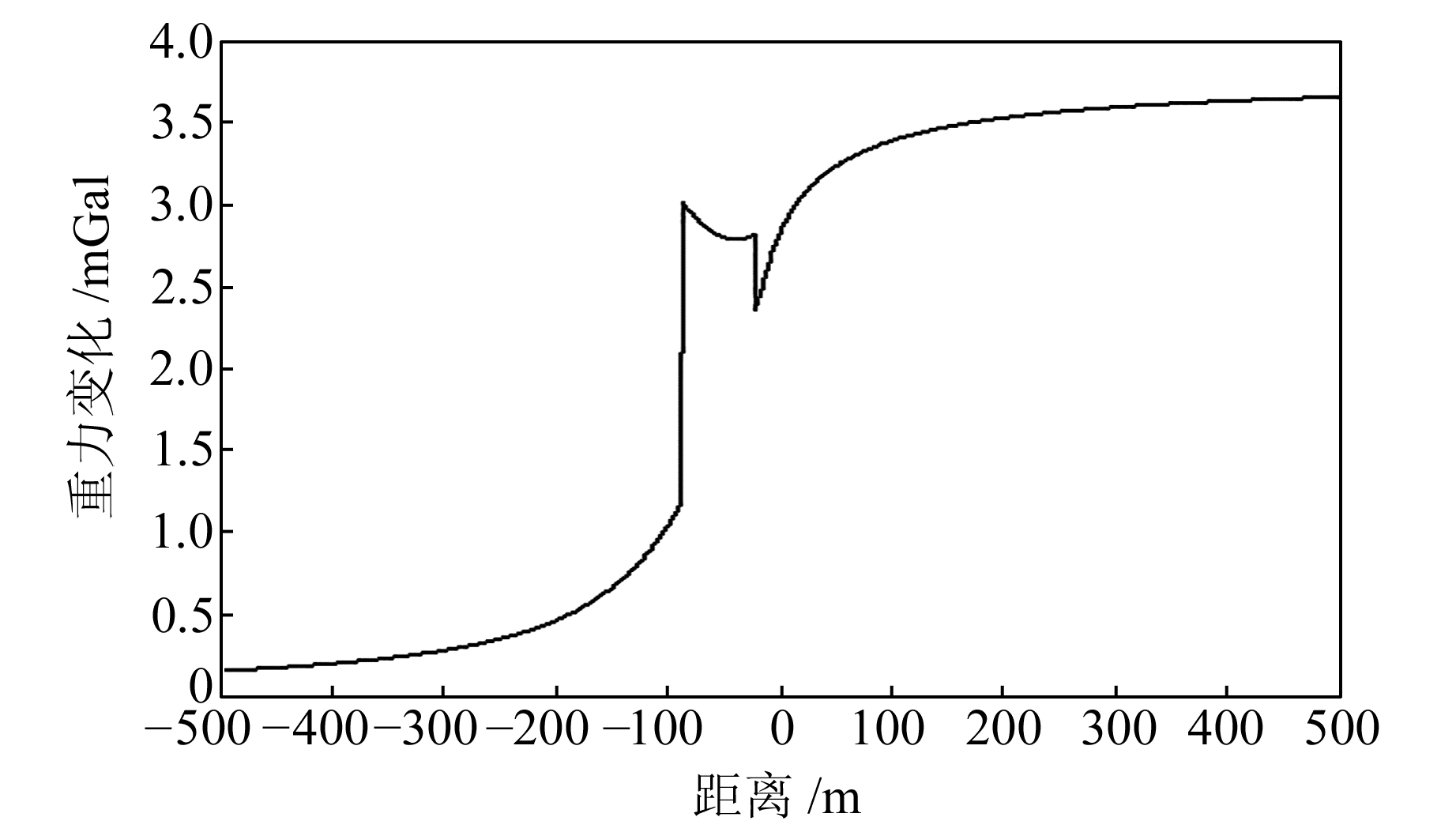
|
图 1 出现畸变的二维倾斜断层重力异常正演 Fig. 1 Illustration of distortion of gravity anomaly forward modeling of inclined fault |
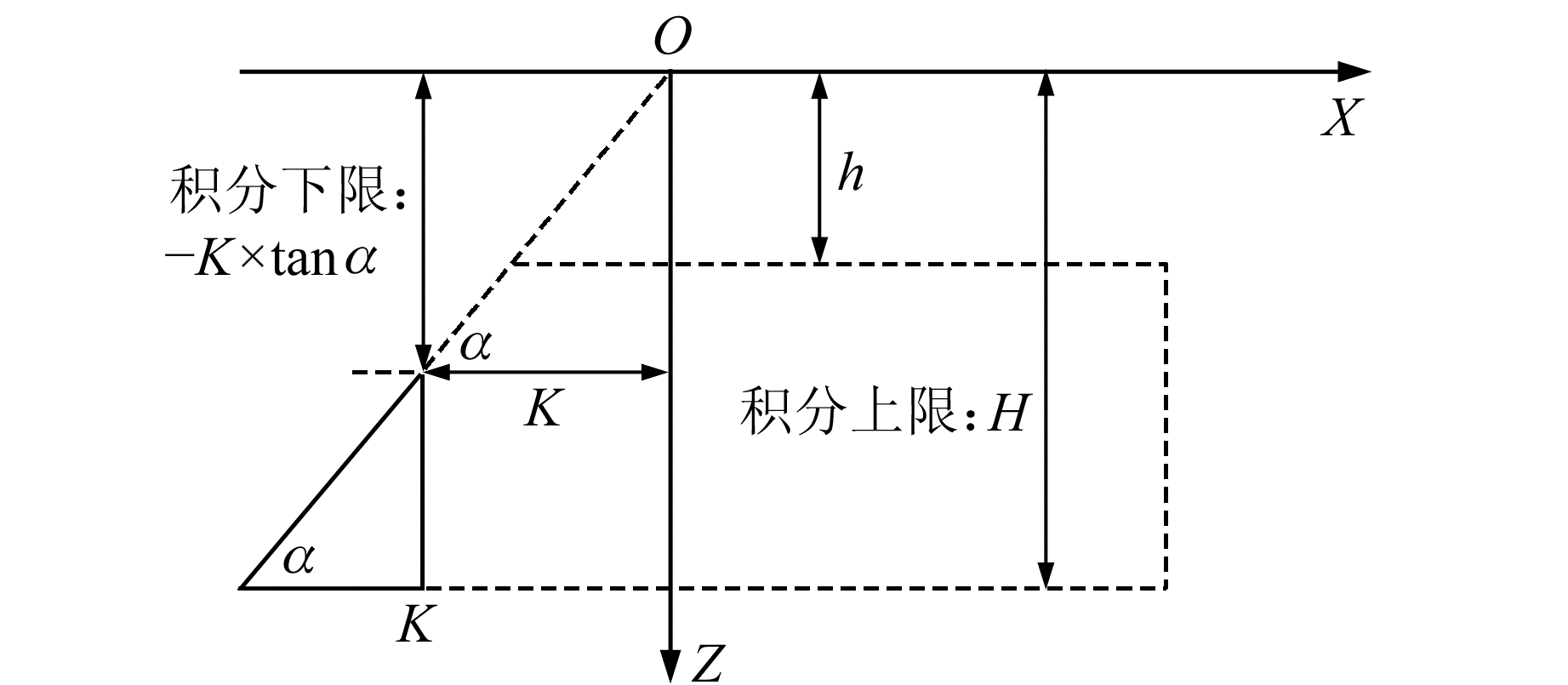
二维倾斜断层重力异常剖面正演坐标系如图 2所示,原点选在断层斜面延伸线与地面交线上,X轴垂直断层走向,Z轴铅垂向下,倾斜断层的夹角为α,上顶高为h,下底高为H。
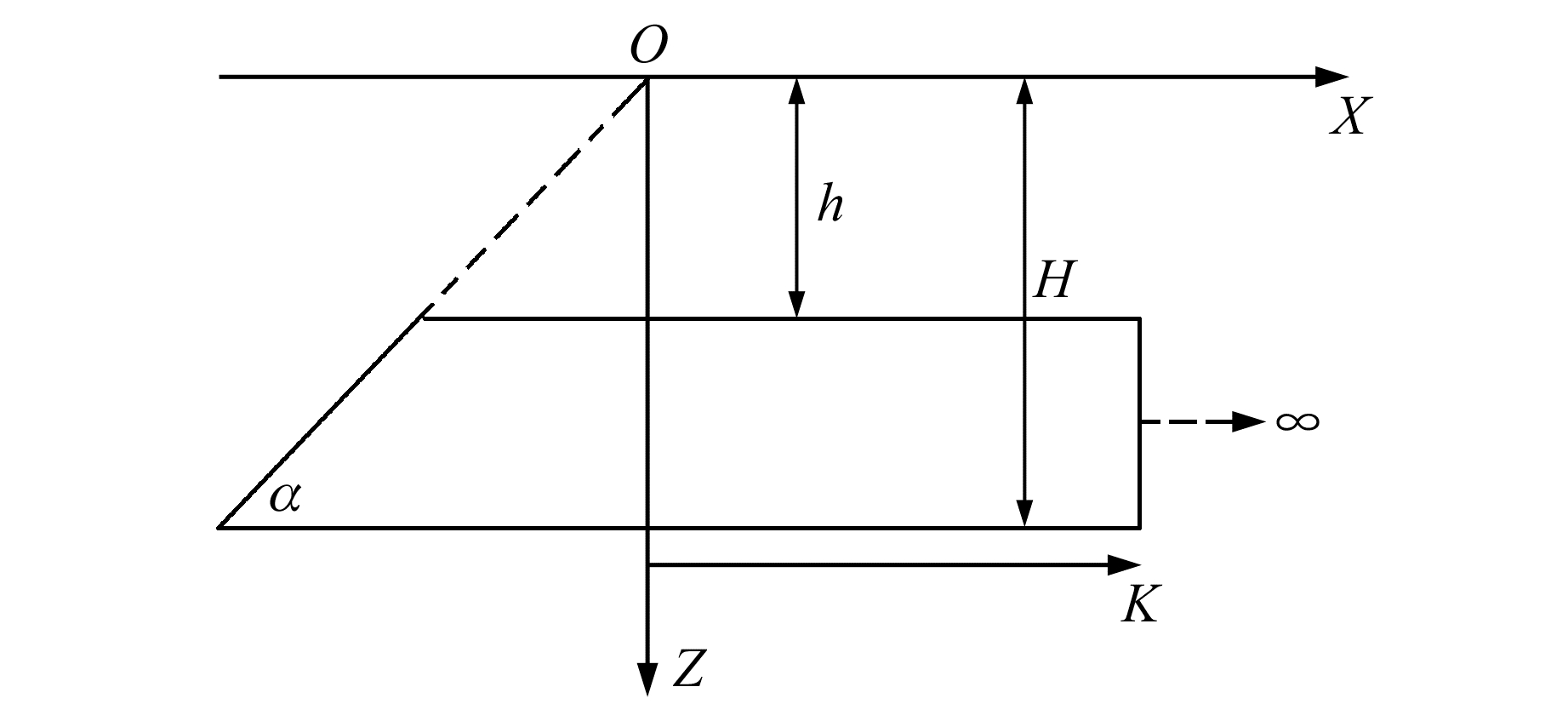
|
图 2 倾斜断层重力异常正演坐标系及相关参数的定义 Fig. 2 Illustration of definition of coordination and other parameters of gravity anomaly forward modeling of inclined fault |
根据初始定义,原始的二维倾斜断层重力异常正演表达式为[2]:
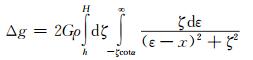
|
(1) |
式中,G为万有引力常数,ρ为倾斜断层与围岩的密度差,x为观测点坐标,(ε, ζ)为倾斜断层场源点坐标。
结合有限长度的二维倾斜断层的特点(即对ε的积分上限不再是∞,而是某一常数K),则原始表达式改写为:
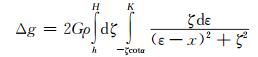
|
(2) |
根据不定积分相关公式[6]:
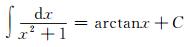
|
(3) |
可得:
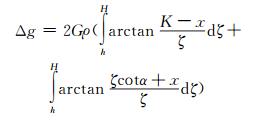
|
(4) |
令
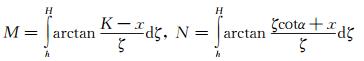
|
仍然结合不定积分相关公式,分别对M和N进行积分,并将积分结果代入式(4),即可得到二维倾斜断层沿X方向上的重力异常正演表达式:
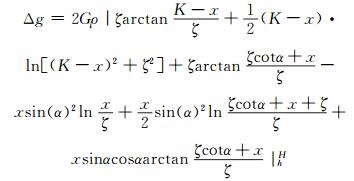
|
(5) |
式中,H>h>0, α∈(0, π/2)。
2 关于常数K取值范围的确定当倾斜断层沿横坐标正方向无限延伸时,不存在K的取值范围的问题; 当K为某一固定常量时,结合对坐标系的定义,其取值范围并非任意。理论上K的取值范围应该为K∈(-∞, ∞)。根据对倾斜断层所处坐标系的定义,不妨将K的取值范围分为以下3个区间(-∞, -Hcotα]、(-Hcotα, -hcotα]和(-hcotα, +∞)。根据式(2),结合实际物理意义,K作为积分上限其值的大小至少应大于-Hcotα,否则通过积分计算得出的重力异常值为负值。如图 3,若-hcotα≥K≥-Hcotα,则式(2)中ζ的积分下限不再是h,而是-Ktanα,此时倾斜断层为图中实线所示的三角形,这与本文最初所假设的断层模型(梯形)不符,其最终的积分结果也将不再等同于式(5)中的形式。因此上述两个区间均不符合实际情况,而满足假设条件的K取值范围应该为(-hcotα, +∞)。
|
图 3 -hcotα≥K≥Hcotα时倾斜断层重力异常正演坐标系及相关参数的定义 Fig. 3 Illustration of definition of coordination and other parameters of gravity anomaly forward modeling of inclined fault when -hcotα≥K≥Hcotα |
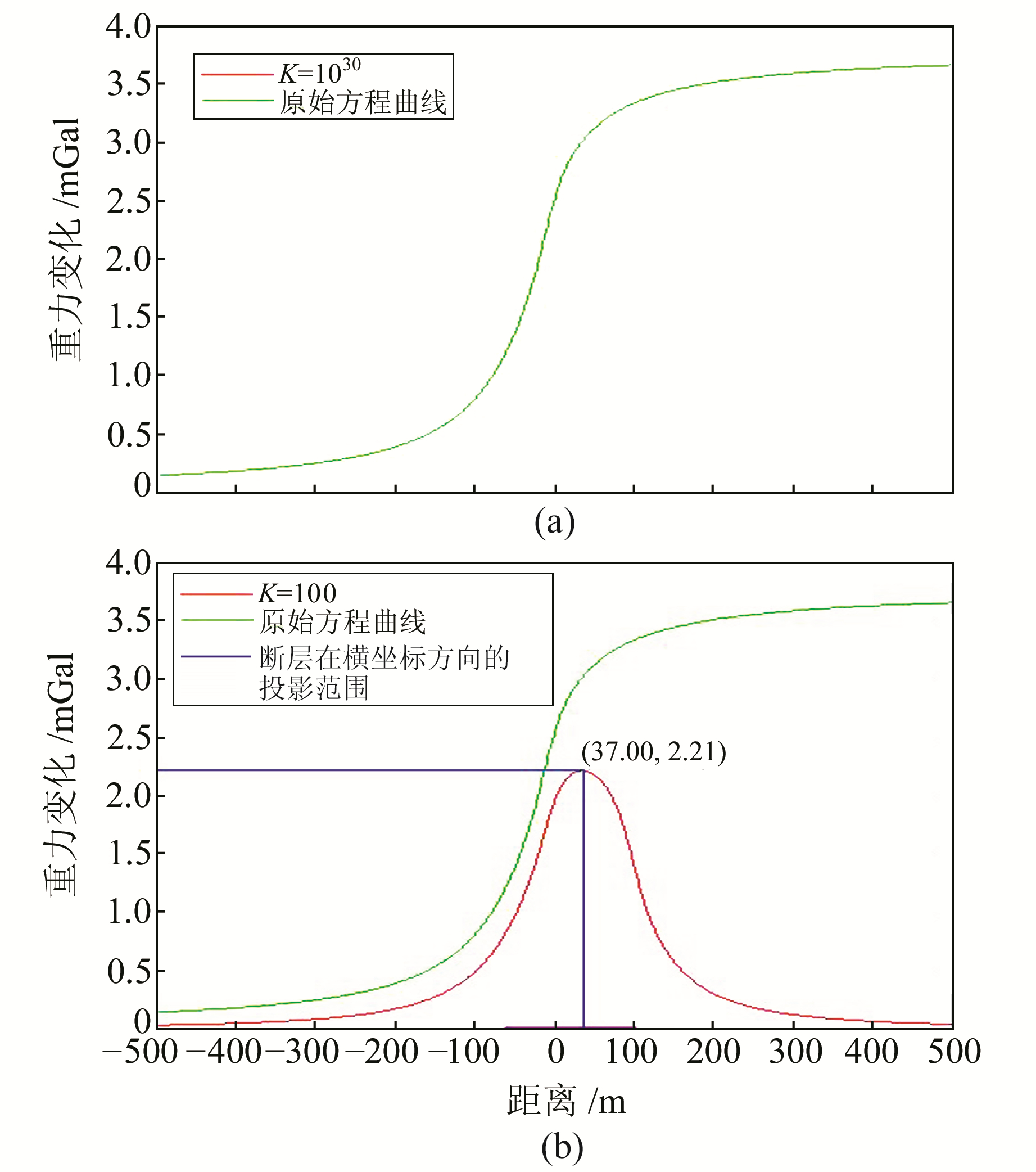
当K取无穷大时,式(5)的计算结果应等同于文献[4-5]的计算结果。为验证推导结果的正确性,本文从两个方面进行验证:1)进行公式推导; 2)绘制重力异常正演图进行比较。
当K→∞时,易证明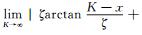
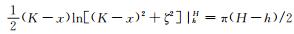
其次,假定h=10 m,H=100 m,剩余密度为1 g/cm3,α=π/3,取K=1030(即在计算机中利用较大的数值近似模拟为无穷大)绘制重力异常正演图(图 4(a))。结果发现,两条曲线几乎重合。综上两点,充分说明了推导结果的正确性。
|
图 4 K=1030和K=100时推导出的表达式绘制曲线与原始表达式绘制曲线的比较 Fig. 4 Illustration of comparison between deduced formula and the initial formula when K=1030 and K=100 |
仍利用上述假定条件,令K=100 m,代入式(5)便可计算出二维倾斜断层力异常正演结果。图 4(b)为有限延伸和无限延伸的重力异常正演曲线比较结果。
从图 4(b)可以看出,在假设条件下,重力异常值呈现倒U型分布,峰值位于约X=37.00 m处,大小约为2.21 mGal。倾斜断层所在投影区域(图中粉红色直线代表区域)的重力异常的变化率较大,超出投影范围所在区域重力异常变化率迅速衰减,逐步趋近于0。
4 结语本文在前人研究的基础上,推导出了沿剖面方向倾斜断层延伸距离为有穷远时的重力异常正演表达式,并论证了“有穷远处”K这一常数的取值范围,同时分析比较了“延伸至无穷远处的倾斜断层”和“延伸至有穷远处的倾斜断层”重力异常剖面正演表达式的异同之处。与原始方程表达式相比,其假设的前提条件无疑更接近自然界中倾斜断层的真实情况。
致谢: 感谢中国地震局第一监测中心黄立人研究员给予的指导和帮助!
| [1] |
陈运泰. 地震预测回顾与展望[J]. 中国科学:地球科学, 2009, 39(12): 1 633-1 685 (Chen Yuntai. Earthquake Prediction:Retrospect and Prospect[J]. Science China Earth Sciences, 2009, 39(12): 1 633-1 685)
(  0) 0) |
| [2] |
曾华黎. 重力场与重力勘探[M]. 北京: 地质出版社, 2005 (Zeng Huali. Gravity Fields and Exploration[M]. Beijing: Geology Press, 2005)
(  0) 0) |
| [3] |
Hubbert M K. A Line-Integral Method of Computing the Gravimetric Effects of Two-Dimensional Masses[J]. Geophysics, 1948, 13(2): 215-225 DOI:10.1190/1.1437395
(  0) 0) |
| [4] |
冯兰天. 台阶(断层)模型重力异常正演计算的一种新算法[J]. 世界地质, 2014, 33(2): 477-483 (Feng Lantian. A New Algorithm for Gravity Anomaly Forward Calculation of Stepped(Fault) Model[J]. Global Geology, 2014, 33(2): 477-483 DOI:10.3969/j.issn.1004-5589.2014.02.026)
(  0) 0) |
| [5] |
苏和明. 倾斜断层重力异常的改进[J]. 地球物理学进展, 2014, 29(5): 2 066-2 071 (Su Heming. Some Improvements on the Formula for Inclined Steps Gravit Anomaly[J]. Progess in Geophysics, 2014, 29(5): 2 066-2 071)
(  0) 0) |
| [6] |
同济大学数学系. 高等数学[M]. 北京: 高等教育出版社, 2007 (Faculty of Mathmatics of Tongji University. Higher Mathmatics[M]. Beijing: Higher Education Press, 2007)
(  0) 0) |
2. SRIT Software Technology Co Ltd, 298 Chaonei Street, Beijing 100010, China
 2017, Vol. 37
2017, Vol. 37

