2. 辽宁科技大学土木工程学院,鞍山市千山中路185号,114051
小波分析因具有多分辨率分析的特点,被广泛应用于变形监测数据处理中,并取得了不错的效果。例如对桥梁风振变形监测数据的处理[1]、高层建筑物的动态监测[2]以及桥梁的变形数据分析[3]。但小波分析主要是提取低频信号的有用信息,而忽略了高频信号的有用信息,使重构的信号失真[4]。小波阈值去噪法对此进行了改进,能对信号的高频部分进行分析,其关键是阈值的选取和小波函数的构造。但传统的小波阈值去噪能力有限,所以很多学者提出了相应的改进方法。在阈值的选取方面进行改进的方法有BayesShrink阈值[5]、MapShrink阈值[6]等; 对于阈值函数的改进方法有软硬阈值折中法、半软阈值法和模平方处理法[7]。这些方法虽然取得了一定的成果,但仍有待进一步改进。有学者在小波阈值去噪中应用了一些新的方法,如袁开明等[8]将模拟退火算法应用于最优阈值的求解; 纪跃波[9]提出了一种分层阈值的小波阈值去噪处理方法; 焦明连等[10]将灰色预测模型和小波分析结合起来。
本文对阈值函数进行了改进,将小波系数与分解层数的相关Lip指数应用到最优阈值的求解中,提出新的阈值选取方法,并通过实例证明该方法的优越性和有效性。
1 小波阈值去噪法 1.1 小波阈值去噪法的原理小波阈值去噪法的基本思想是:带有噪声的信号在经小波分解后,得到代表噪声的高频系数和代表有用信号的低频系数; 于是可以找到一个合适的阈值,对小波分解后的系数进行阈值量化处理,即绝对值小于给定阈值的系数置为0,而让绝对值大于给定阈值的系数保留或者收缩,得到估计的小波系数; 最后用这些估计的小波系数重构信号,即达到去噪的目的。
1.2 小波阈值去噪法的步骤1) 小波分解。选择一种小波函数,对信号进行N层分解。常用的小波基函数有symN、dbN和coifN,分解层数一般为1~4层。
2) 阈值的选取。目前常用的阈值选取准则有sqtwolog准则、rigrsure准则、heursure准则和minimaxi准则等[11]。4种阈值准则虽然在不同程度上取得了不错的去噪效果,但仍然存在一些不足。sqtwolog准则以及heursure准则都是将全部的系数进行处理[12],这样的处理方式虽然可以较强地去除噪声,但同时也扼杀了一些有用信号的系数。rigrsure准则以及minimaxi准则只是折中地处理部分小波系数,可以防止有用信号在去噪过程中被扼杀,但容易出现去噪不明显的现象。
针对4种阈值准则在去噪中存在的不足,本文提出了基于Lip指数阈值寻优法确定每层阈值。该方法是根据有用信号对应的小波系数在各尺度上的相关性较强,而噪声对应的小波系数在各尺度上无相关性,在各尺度上进行相关性运算,从而减小噪声的系数,能够很好地滤去噪声,保留原始信号。由文献[13]可知:
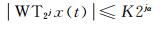
|
(1) |
式中,WT2jx(t)为第j层小波分解系数,α为Lip指数,K为常数。Lip指数与信号的平滑度有关,α越大,信号越平滑。对于一般的信号,有用信号的Lip指数为正,即随着分解尺度的增大,有用信号的小波系数也随之增大; 而带有噪声的信号Lip指数为负,即随着分解尺度的增大,白噪声信号系数随之减小。
白噪声的Lip指数满足[14]:
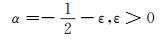
|
(2) |
由式(1)和式(2)可知:
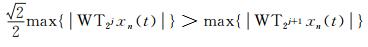
|
(3) |
式中,第j层噪声所对应的小波系数是WT2jxn(t)。由式(3)可以看出,第j+1层对应的噪声小波系数的最大值小于噪声对应的第j层小波系数最大值的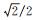
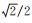
3) 阈值函数的确定。选择合适的阈值函数对小波系数进行阈值处理。常用的阈值函数有硬阈值函数和软阈值函数。两者虽然已经在实际工程中得到广泛的应用,但其本身还有一些缺陷[15]。本文提出改进的阈值函数:
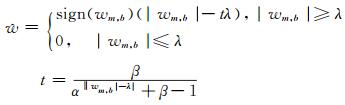
|
(4) |
式中,参数α、β均为大于1的常数,并且可以根据实际情况进行调整。

|
(5) |
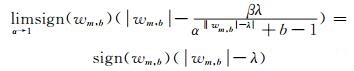
|
(6) |
从式(5)和式(6)可以看出,当α→∞时,式(4)接近硬阈值函数; 当α→1时,式(4)接近软阈值函数,并且新的阈值函数还可以通过调整α和β的值来得到不同的去噪效果。
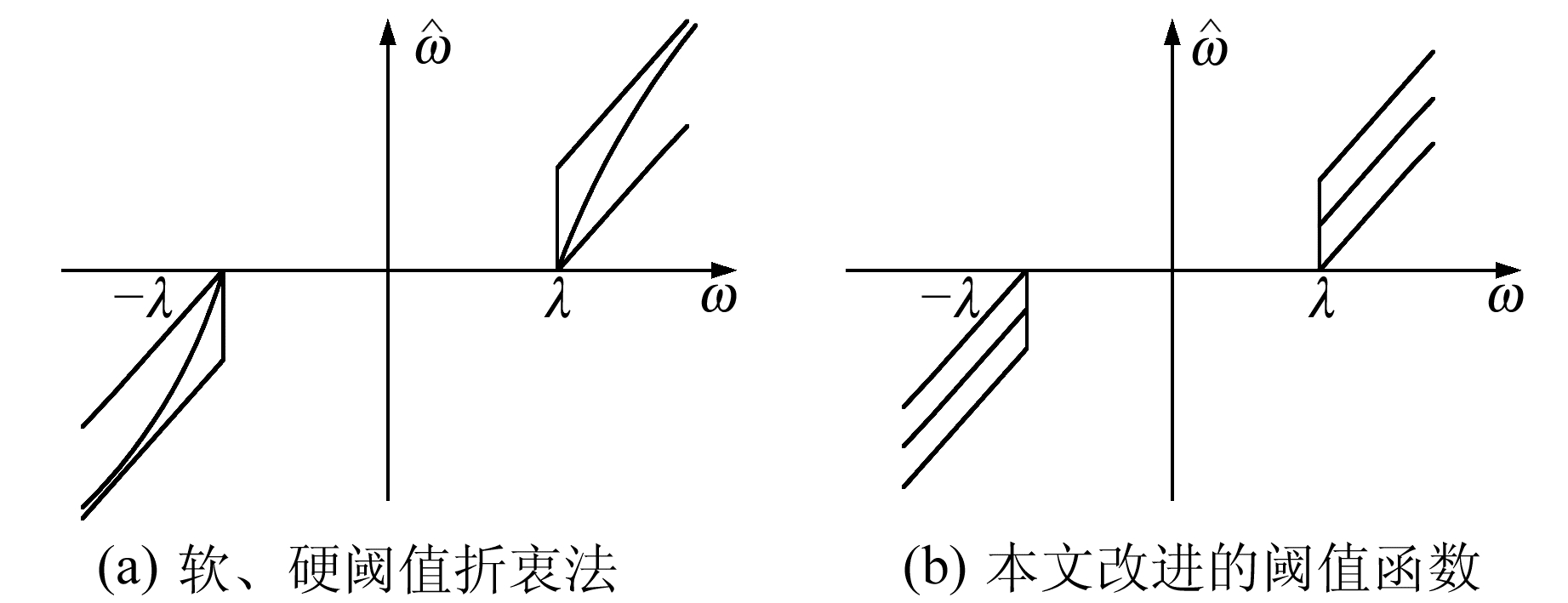
由图 1可以看出,软、硬阈值折衷法相对传统的阈值函数,通过调整α的值可以达到不同程度的去噪效果,但是其只是软、硬阈值的折衷。显然α=1时,此函数在±λ处是连续的; 当α≠1时,阈值函数在±λ处是不连续的,这样重构的信号会引起一定程度的振荡。
|
图 1 改进阈值函数 Fig. 1 Improved threshold function |
本文改进阈值函数以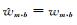
4) 小波重构。降噪处理后的系数通过小波重建恢复原始信号。
2 算例分析和比较利用抚顺市某广场的沉降观测数据进行小波去噪处理,测量仪器是天宝(DINI12)GPS接收机,观测时间为2012-12-11~2013-04-26,观测频率为每h一次,每天观测6 h,共256期。利用小波阈值去噪法对带有误差的沉降数据进行去噪处理。
2.1 小波阈值去噪性能的评价标准以信噪比SNR和均方根误差RMSE为标准,评定改进的阈值函数的去噪效果。信号去噪后SNR越大、RMSE越小,去噪的效果越好[16]。
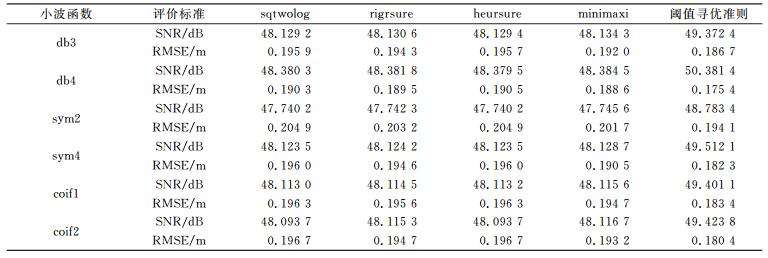
2.2 各种阈值选取准则去噪效果分析 2.2.1 不同小波函数下各种阈值选取准则效果分析使用MATLAB软件,以含有噪声的沉降观测数据为信号,采用sqtwolog、rigrsure、heursure、minimaxi及本文提出的阈值寻优准则,选取不同的小波函数,采用传统的硬阈值函数,分解层数取3进行计算,去噪效果如表 1所示。
|
|
表 1 不同小波基下的5种阈值准则的去噪效果 Tab. 1 Denoising effect of five threshold rules under different wavelet base |
从表 1可以看出,db4小波函数在5种不同的阈值选取准则下,去噪效果最好,并且db4小波函数下阈值寻优准则去噪后的效果最好。从而验证了基于Lip指数的阈值寻优方法的优越性。
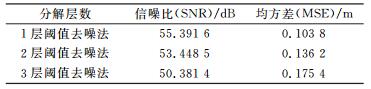
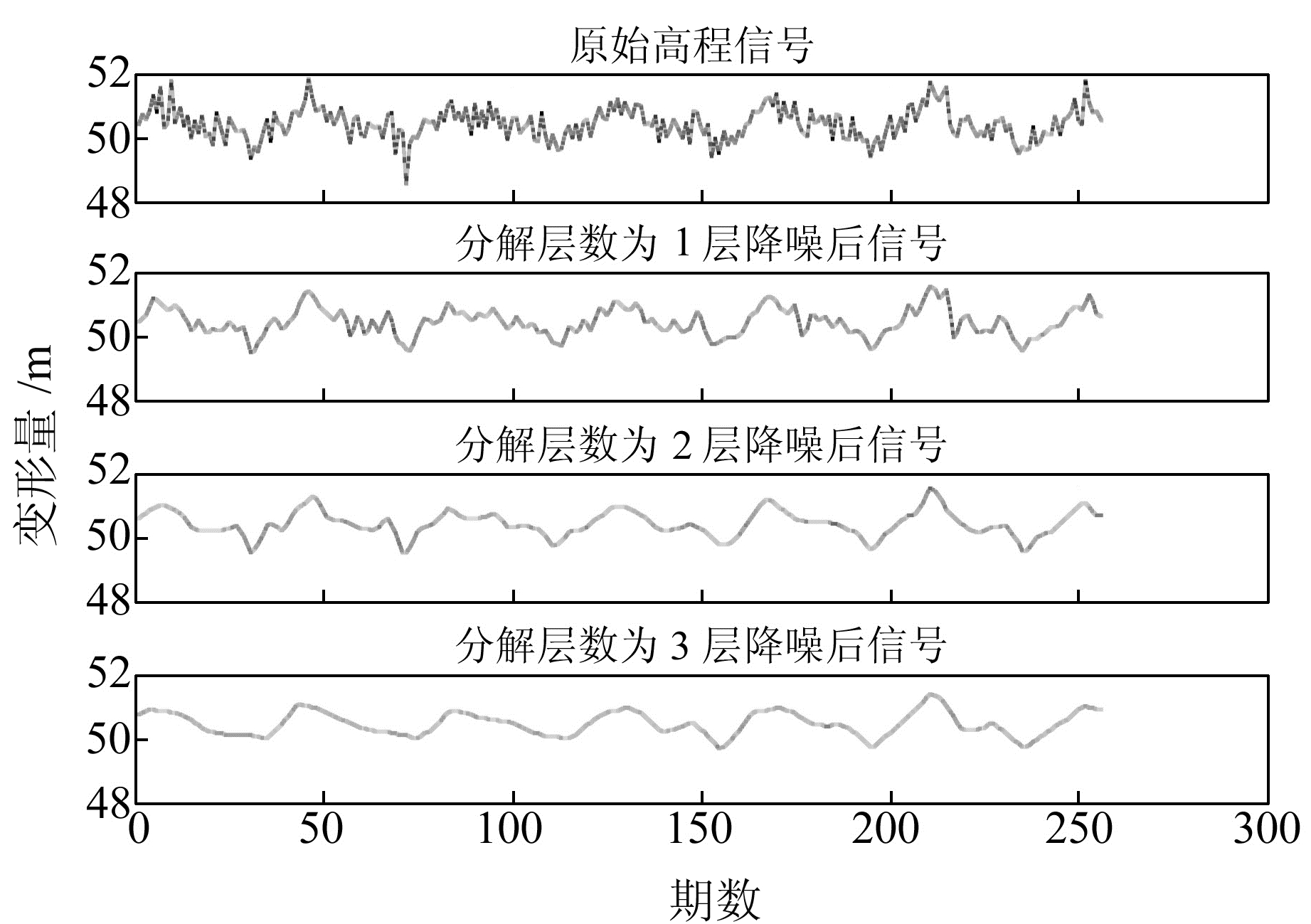
2.2.2 不同分解层数下各种阈值准则效果分析选取db4小波函数,分解层数为1~3层,采用阈值寻优准则进行计算,去噪效果如图 2所示。从图 2可以看出,3种分解层数去噪后的信号比原始信号更光滑,达到了一定的去噪效果; 分解层数为3层去噪后信号虽然最光滑,但失去了原有信号的变化趋势。从表 2也能明显看出,3层分层阈值去噪法信噪比最低,这是因为分解层数过大,会使有用信号的高频部分在阈值处理过程中被去掉,造成信号失真。分解层数为1层去噪后的信噪比虽然最高,但是去噪后的信号却是最粗糙的,这是因为分解层数过少,很多带有高频部分的系数保留在低频部分中,去噪不彻底。分解层数为2层在去噪的过程中不仅提高了信噪比,而且保留了有用信号的高频部分,防止了信号失真。所以,分解层数为2层时,去噪效果最好。
|
图 2 不同分解层数的分层阈值法去噪效果 Fig. 2 Denoising effect of hierarchical threshold of different decomposition level |
|
|
表 2 不同分解层数分层阈值法降噪性能比较 Tab. 2 Denoising performances of hierarchical hreshold of different decomposition level |
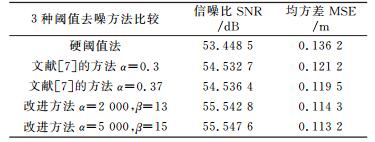
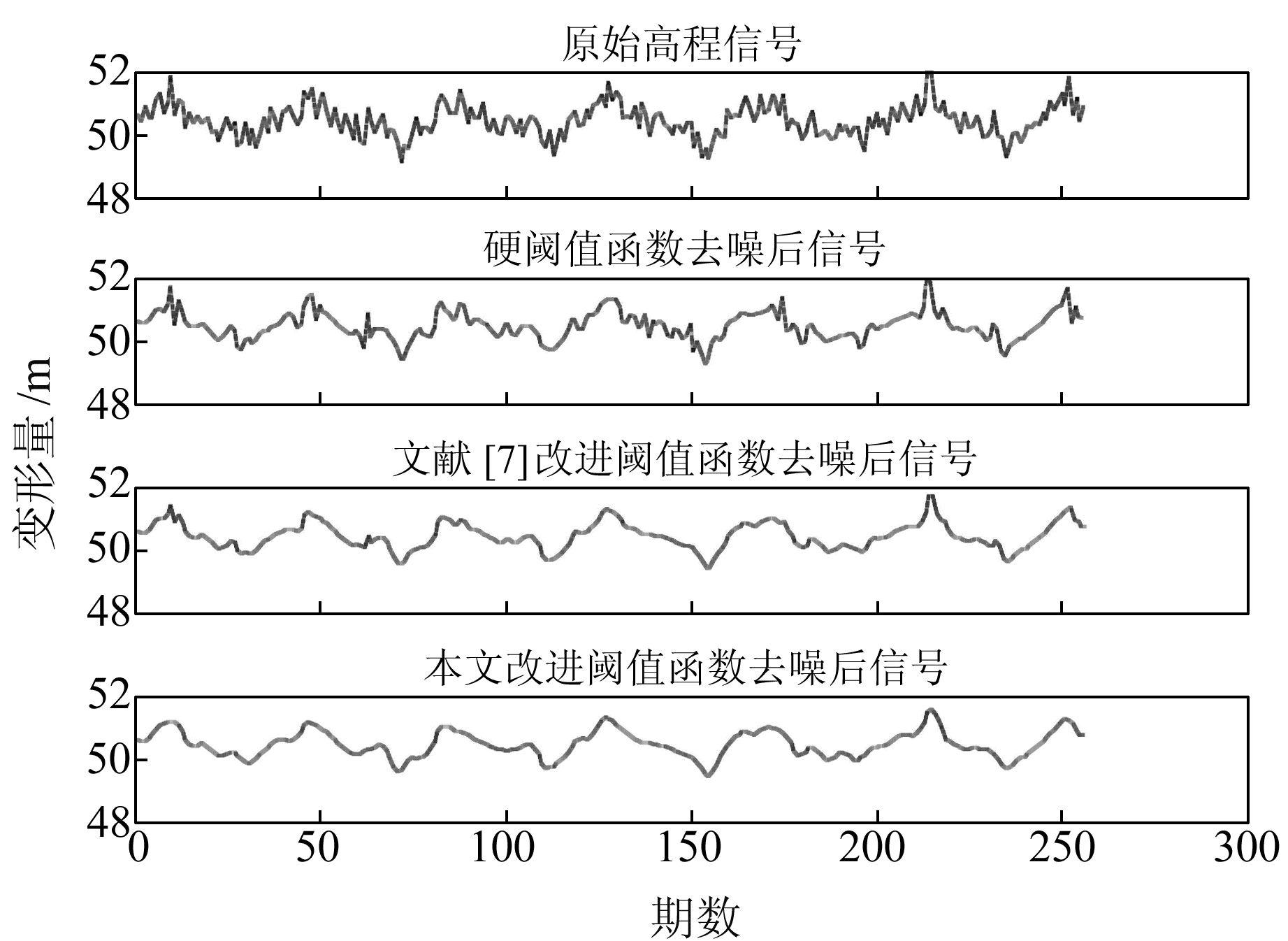
选取db4小波函数,分解层数为2层,阈值选取准则为阈值寻优准则,采用传统的硬阈值函数、文献[7]改进的阈值函数和本文改进的阈值函数进行去噪处理,结果如图 3所示。从图 3可以看出,由于硬阈值函数在处理过程中得到的估计小波函数不连续,重构后的信号会产生一些振荡,去噪后的信号不够光滑。文献[7]的方法和本文改进方法克服了以上两种缺点,去噪后的信号较硬阈值函数去噪后的信号光滑,达到了较好的去噪效果。从表 3也可以看出,文献[7]的方法和本文改进方法去噪后的信噪比和均方差均优于传统的软、硬阈值函数,同时本文改进方法去噪后的信噪比最高,均方差最小,且在一定范围内选取适当的α和β值,去噪效果会更明显。
|
图 3 3种阈值函数去噪效果 Fig. 3 Denoising effect of three threshold functions |
|
|
表 3 3种阈值去噪方法比较 Tab. 3 Denoising performances of three threshold functions |
1) 变形监测数据会被误差所掩盖,使用小波阈值去噪方法,不但可以将原始数据中的噪声剔除,而且能提取带有噪声观测值中的有用信息,得到观测对象精确的变化趋势,适合变形监测数据处理。
2) 本文对小波阈值去噪法进行了两个方面的改进——Lip指数阈值寻优法和改进的阈值函数,比传统的阈值选取规则去噪及软、硬阈值去噪方法在信噪比和均方差上都有所提高。本文改进的新阈值函数有两个待定系数α和β,它们会直接影响到去噪的效果,如果选择得当会更加突出新方法的优越性。
3) 小波函数、分解层数、阈值选择准则和阈值函数的选取都会直接影响到小波去噪的效果,如何选取最优小波函数及分解层数还有待进一步研究。
| [1] |
李振, 朱峰, 陈家君. 基于小波变换的桥梁风振变形监测数据处理[J]. 测绘通报, 2011(11): 18-20 (Li Zhen, Zhu Feng, Chen Jiajun. Analysis and Processing of Wind Shock Deformation Monitoring Data for Bridge Based on Wavelet Transform[J]. Bulletin of Surveying and Mapping, 2011(11): 18-20)
(  0) 0) |
| [2] |
黄声享, 刘经南, 柳响林. 小波分析在高层建筑物动态监测中的应用[J]. 测绘学报, 2003, 32(2): 153-157 (Huang Shengxiang, Liu Jingnan, Liu Xianglin. Deformation Analysis Based on Wavelet and Its Application in Dynamic Monitoring for High-Rise Buildings[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 153-157 DOI:10.3321/j.issn:1001-1595.2003.02.012)
(  0) 0) |
| [3] |
王建波, 栾元重, 许君一, 等. 小波分析桥梁变形监测数据处理[J]. 测绘科学, 2012, 37(3): 83-85 (Wang Jianbo, Luan Yuanzhong, Xu Junyi, et al. Wavelet Analysis on Data Processing of Bridge Deformation Monitoring[J]. Science of Surveying and Mapping, 2012, 37(3): 83-85)
(  0) 0) |
| [4] |
唐进元, 陈维涛, 陈思雨, 等. 一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击, 2009, 28(7): 118-121 (Tang Jinyuan, Chen Weitao, Chen Siyu, et al. Wavelet-Based Vibrationsignal Denoising with a New Adaptive Thresholding Function[J]. Journal of Vibration and Shock, 2009, 28(7): 118-121 DOI:10.3969/j.issn.1000-3835.2009.07.025)
(  0) 0) |
| [5] |
Nasri M, Nezamabadi-Pour H. Image Denoising in the Wavelet Domain Using a New Adaptive Thresholding Function[J]. Neurocomputing, 2009, 72(4-6): 1 012-1 025 DOI:10.1016/j.neucom.2008.04.016
(  0) 0) |
| [6] |
Shark L K, Yu C. Denoising by Optimal Fuzzy Thresholding in Wavelet Domain[J]. Electronics Letters, 2000, 36(6): 581-582 DOI:10.1049/el:20000451
(  0) 0) |
| [7] |
朱艳芹, 杨先麟. 几种基于小波阈值去噪的改进方法[J]. 电子测试, 2008(2): 18-22 (Zhu Yanqin, Yang Xianlin. Several New Methods Based on Wavelet Thresholding Denoising[J]. Electronic Test, 2008(2): 18-22 DOI:10.3969/j.issn.1000-8519.2008.02.005)
(  0) 0) |
| [8] |
袁开明, 舒乃秋, 孙云莲, 等. 基于阈值寻优法的小波阈值去噪分析[J]. 武汉大学学报:工学版, 2015, 48(1): 74-80 (Yuan Kaiming, Shu Naiqiu, Sun Yunlian, et al. Wavelet Denoising Based on Threshold Optimization Method[J]. Engineering Journal of Wuhan University, 2015, 48(1): 74-80)
(  0) 0) |
| [9] |
纪跃波. 小波包的频率顺序[J]. 振动与冲击, 2005, 24(3): 96-98 (Ji Yuebo. Frequecy Order of Wavelet Packet[J]. Journal of Vibration and Shock, 2005, 24(3): 96-98 DOI:10.3969/j.issn.1000-3835.2005.03.028)
(  0) 0) |
| [10] |
焦明连, 蒋廷臣. 基于小波分析的灰色预测模型在大坝安全监测中的应用[J]. 大地测量与地球动力学, 2009, 29(2): 115-117 (Jiao Minglian, Jiang Tingchen. Applcation of Greymodel Based on Wavelet Analysis in Dam Safety Monitoring[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 115-117)
(  0) 0) |
| [11] |
章浙涛, 朱建军, 匡翠林, 等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报, 2014, 43(1): 13-20 (Zhang Zhetao, Zhu Jianjun, Kuang Cuilin, et al. Multi-threshold Wavelet Packet De-Noising Method and Its Application in Deformation Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 13-20)
(  0) 0) |
| [12] |
Beenamol M, Prabavathy S, Mohanalin J. Wavelet Based Seismic Signal De-Noising Using Shannon and Sallis Entropy[J]. Computers and Mathematics with Applications, 2012, 64(11): 3 580-3 593 DOI:10.1016/j.camwa.2012.09.009
(  0) 0) |
| [13] |
张德丰. Matlab小波分析[M]. 北京: 机械工业出版社, 2009 (Zhang Defeng. Matlab Wavelet Analysis[M]. Beijing: China Machine Press, 2009)
(  0) 0) |
| [14] |
Stefan W, Chen K W, Guo H B, et al. Wavelet-Based De-noising of Positron Emission Tomography Scans[J]. Journal of Scientific Computing, 2012, 50(3): 665-677 DOI:10.1007/s10915-011-9529-8
(  0) 0) |
| [15] |
邵鸿翔, 高宏峰. 改进小波阈值去噪方法处理FBG传感信号[J]. 激光与红外, 2014, 44(1): 73-76 (Shao Hongxiang, Gao Hongfeng. Processing of FBG Sensor Signal with Improved Wavelet Threshold De-Noising Method[J]. Laser & Infrared, 2014, 44(1): 73-76 DOI:10.3969/j.issn.1001-5078.2014.01.016)
(  0) 0) |
| [16] |
吴继忠. GPS观测数据的小波阈值法消噪[J]. 大地测量与地球动力学, 2009, 29(4): 79-82 (Wu Jizhong. De-Noising of GPS Observations with Wavelet Threshold Method[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 79-82)
(  0) 0) |
2. College of Civil Engineering, University of Science and Technology Liaoning, 185 Mid-Qianshan Road, Anshan 114051, China
 2017, Vol. 37
2017, Vol. 37