2. 武汉大学测绘学院,武汉市珞喻路129号,430079
当前各种隧道变形预测模型层出不穷,如传统分析方法、根据沉降测量数据建立统计模型的岩土力学方法,但受小样本、经验公式及不完整的力学构造假设等制约,预测精度有限[1]。梅文勇[2]基于新曲儿岔隧道地表沉降回归分析,实施隧道口浅埋地段的沉降监测,并确定相关的实施控制标准。王源等[3]通过分析九华山隧道现场爆破振动监测数据,利用4种不同相关因子进行回归分析处理,得到等间距采样点变化规律,但模型结构简单且缺失全综合分析处理。威纲等[4]通过对测量数据进行概率分析,建立时间序列分析预测模型,但对突发改变的时间序列分析处理预测精度结果存在缺陷。卡尔曼滤波法对于当前估计状态具有最小方差无偏特征,通过递推方式计算且简单有效,在进行实时拟合估计后对未来状态进行预测,但滤波的合理应用需要精确的已知模型以及噪声统计[5]。灰色系统理论在处理少样本、贫信息、不确定性等问题时有较好的效果,被广泛应用于隧道监测数据处理中,但需要综合考察监测数据的相关统计规律、理论的适应性和局限性[6]。近年来,人工免疫、蚁群算法、神经网络等智能算法在隧道变形预测中得到较好的应用[7-9],但智能算法容易陷入局部最优、模型鲁棒性较低、理论基础知识并不完善。谭鹏等[10]提出支持向量机的隧道变形预测模型,预测精度有较大提高,但核函数受Mercer定理限制,同时核函数的构建与合理组合、核参数的确定严重影响模型的预测精度。相关向量机具有小样本、非线性、参数少、稀疏性高等特点[11],且核函数不受Mercer定理限制、模型计算过程和结果都有相关概率解释,因此本文建立基于灰色关联和相关向量机的隧道地表沉降预测模型。通过实例结果的精度指标分析,证实该方法具有更好的预测精度。
1 灰色关联和相关向量机模型 1.1 灰色关联度原理设系统特征序列为X0=(x0(t1), x0(t2), …, x0(tn)),相关因素特征序列为Xi=(xi(t1), xi(t2), …, xi(tn)),其中n为数据个数,tn为第n个监测数据时间,i为影响因素种类。
由于各影响因素之间的量纲不同,为归纳统一样本的统计分布性,加快梯度下降以求解最优解速度,采用初始值法对数据进行处理。该方法还能适当降低计算量和减小误差。
影响因素关联系数γ(x0(k), xi(k))为:

|
(1) |
式中,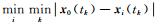
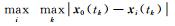
设训练样本集输入数据为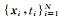
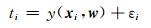
|
(2) |
根据样本数据建立相关向量机学习模型y(x, w):
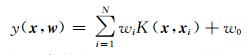
|
(3) |
式中,w为权参数向量,K(x, xi)为核函数,不需要满足Mercer定理条件的限制。
由于ti服从独立分布,则t的似然函数可以表示为:

|
(4) |
式中,基函数Φ =(Φ1, Φ2, …, ΦN)T,基函数向量Φi=(1, K(xi, x1), …, K(xi, xn))。
如果对权向量w直接求解最大似然估计,容易导致模型过度拟合,与实际数据集偏差较大。学习相关向量机模型期间,似然边缘函数进行最大化算法是第Ⅱ类最大似然估计方法,故超参数向量α的边缘似然分布为:
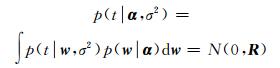
|
(5) |
式中,每一个相互独立的超参数分别控制对应权参数先验分布,协方差R =σ2E + ΦH-1ΦT。
最大化求解超参数向量边缘似然分布,通过设置迭代运算,计算超参数向量和高斯噪声误差,最后解得优化参数:
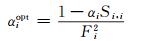
|
(6) |

|
(7) |
式中,Si, i为后验分布S的第i个权值对角元素,Fi为后验分布均值期望值的第i个权参数,迭代更新得出超参数向量和误差向量。
机器模型学习方法根据迭代公式进行,不断更新式(6)和式(7),及时更新后验分布均值和对应协方差,设定适量的迭代次数或者达到规定的收敛区间,计算最后输出的结果。在目标函数训练结束之后,大部分超参数值趋于无穷大,对应权值为0,此时删除基函数,小部分权值不为0的函数对应的向量被称为相关向量机[13]。
融入完善的核函数可以将低维空间数据映射到高维空间,合理计算相应空间变化。通过矩阵运算计算核函数,与样本输入数据的维数无关,可以有效处理高维输入数据带来的难题并能适当减少计算量。高斯核函数和多项式核函数分别在局部核函数与全局核函数中广泛应用,对其进行加权组合,能够提高模型预测精度:
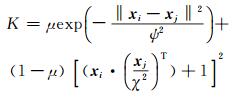
|
(8) |
式中,前部分为高斯核函数,μ、ψ为高斯核函数所占权重与核宽度,后部分为多项式核函数,χ为多项式核宽度,xi、xj为样本数据集输入向量,核函数参数为[μ, ψ, χ]。
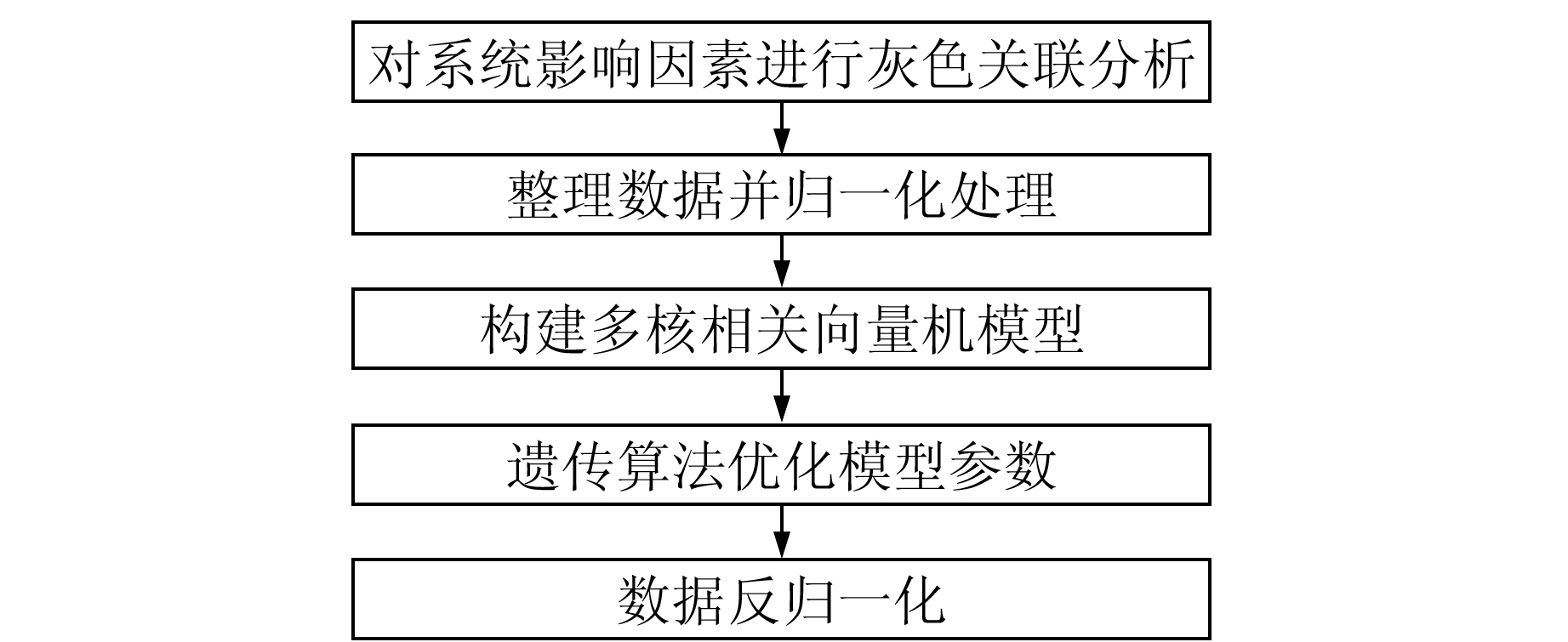
1.3 模型结构和优化参数利用灰色关联度算法计算各影响因素对沉降槽的变化关联度,算法流程如图 1所示。
|
图 1 GR-RVM预测模型结构 Fig. 1 Sketch of GR-RVM's prediction model |
由图 1可知,首先通过对监测点实测数据进行归一化处理,可减小无量纲的影响并提高计算速度,然后根据灰色关联度算法确定沉降槽i变化的主要影响因素,构建加权核函数实现非线性转换和有效解决高维难题,利用遗传算法来搜索相关向量机模型的最优参数,最后将预测结果进行反归一化处理得到预测值。
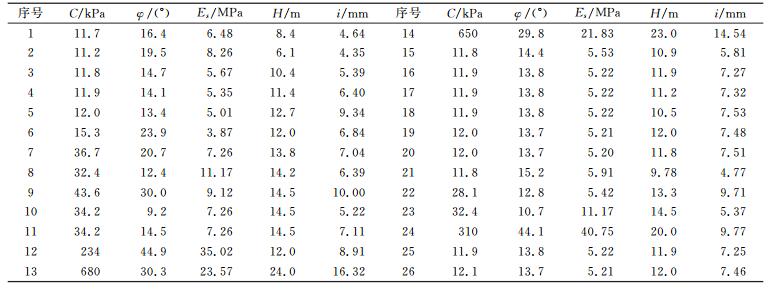
2 实例分析 2.1 灰色关联度计算采用文献[14]中26期连续施工监测点的实测数据(南京地铁、上海地铁和广州地铁盾构工程)进行分析处理,地表沉降槽i的观测参数有土层黏结力C、内摩擦角φ、割线弹模Es、隧道埋深H,实验样本参数见表 1。
|
|
表 1 地表沉降的实验样本参数 Tab. 1 The experimental sample parameters of surface subsidence |
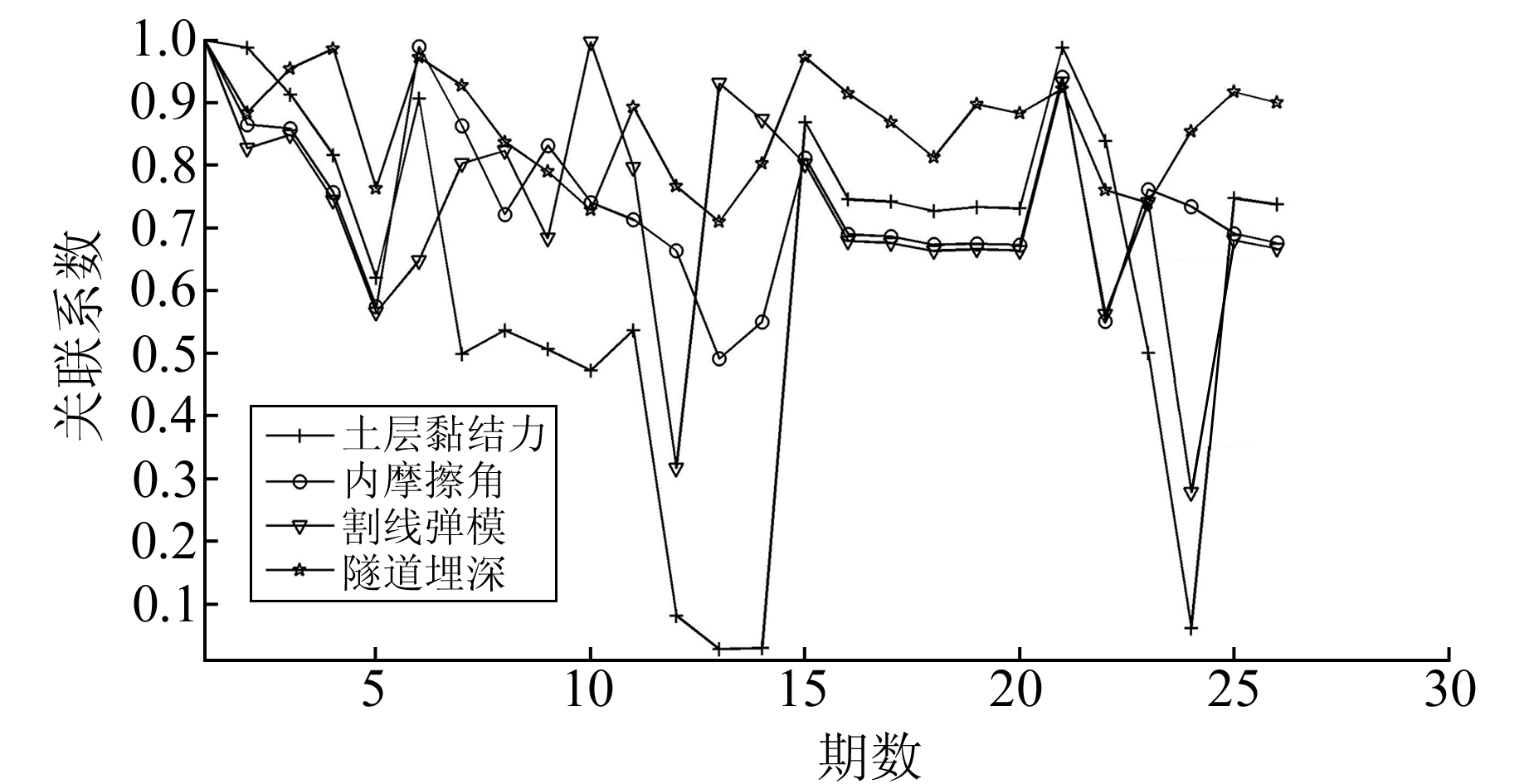
根据实验样本数据计算各影响因素对沉降槽i的变化灰色关联系数,各影响因素与地表沉降变化的关联程度如图 2所示。由图 2可见,影响因素内摩擦角φ、割线弹模Es和隧道埋深H与沉降槽变化i紧密关联,反映内部机理之间的影响,而计算土层黏结力C关联系数偏低且多次接近于0。
|
图 2 各影响因素灰色关联系数计算结果 Fig. 2 The results of gray relational coefficient of each influencing factor |
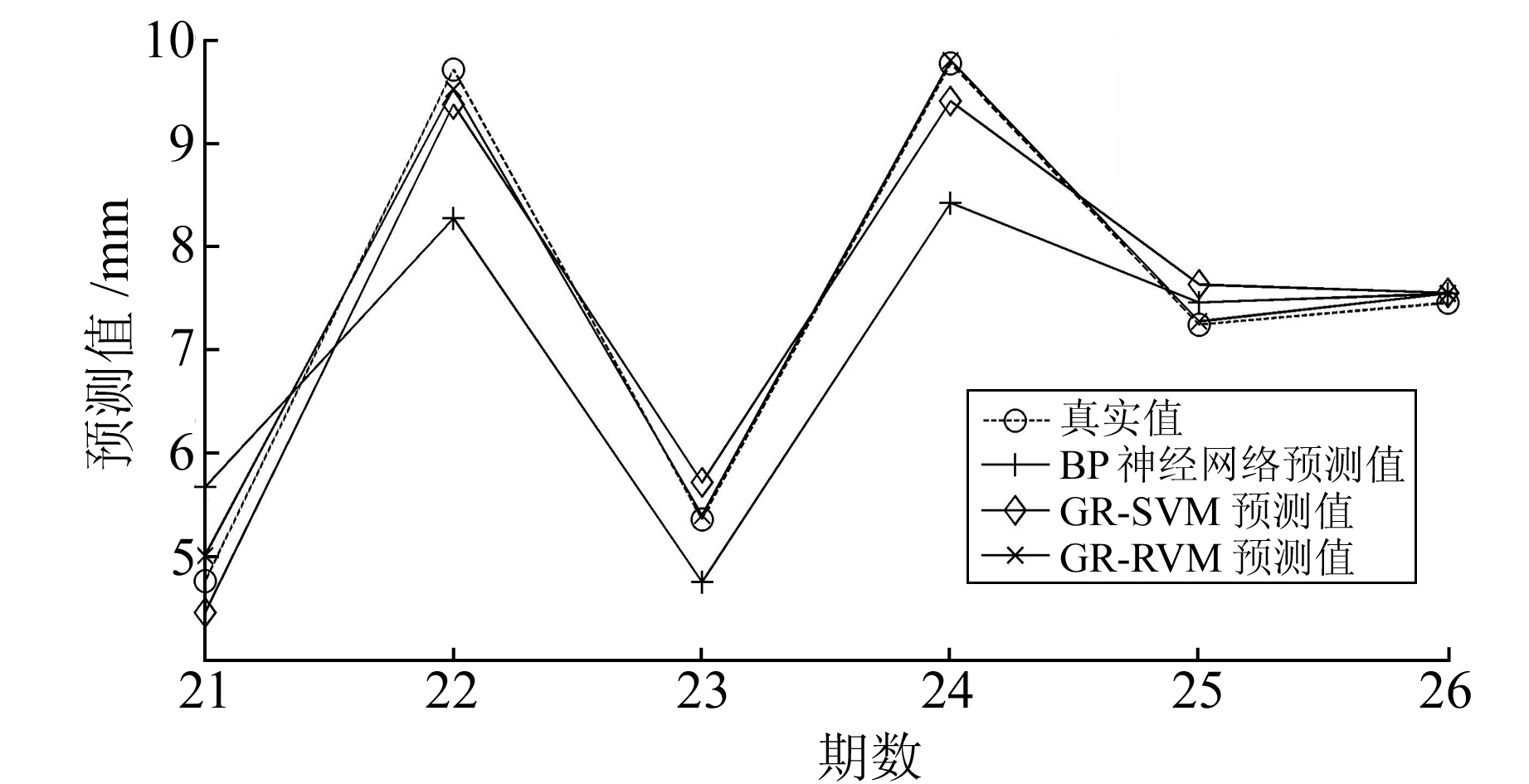
根据前20个训练样本数据建立GR-RVM拟合模型,利用遗传算法优化训练模型参数,参数设置原则及要求见文献[15],迭代34次算法收敛,最优参数为[0.642, 0.240, 0.116]。其余6个测试样本数据作为模型的测试能力,输入测试样本数据,输出对应预测结果。GR-RVM方法、BP神经网络方法和GR-SVM方法预测结果如图 3所示。
|
图 3 各模型方法预测结果 Fig. 3 The prediction results of each model method |
由图 3可知,BP神经网络方法预测结果与真实值相差较大,在处理小样本、贫信息数据时存在较大不足; GR-SVM方法大部分预测结果较好,模型在解决高度非线性问题时有较大提升; GR-RVM方法预测结果与真实值基本吻合,整体预测效果较好。
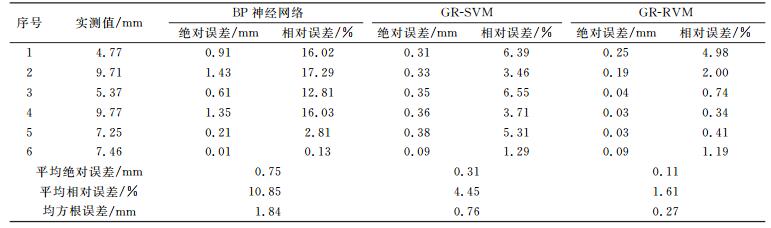
2.3 结果分析采用绝对误差、相对误差、平均绝对误差、平均相对误差及均方根误差等精度评价指标评定3种方法的预测精度,结果见表 2。
|
|
表 2 预测结果及精度评价指标 Tab. 2 Predictive results and accuracy evaluations |
由表 2可知,BP神经网络方法大部分预测结果不理想,智能算法容易陷入局部最优,在处理小样本及泛化能力等方面存在不足; GR-SVM方法的绝对误差较好,但相对误差一般,对正确反映预测结果质量还有改进空间,但机器学习算法在解决小样本、非线性问题有较强的泛化能力与较好的鲁棒性; GR-RVM方法与真实值的偏离程度很小,能更确切地反映预测的准确程度,多项精度评定指标值均较小,比BP神经网络方法、GR-SVM方法均有提高。
3 结语1) 通过对实验数据进行灰色关联分析,能够有效处理信息不是完全明确的灰色系统,对于小样本、规律性不强指标的评价问题有较高的决策准确性,对于模型结构以及预测准确性有较大改善。
2) 基于相关向量机的地表沉降预测模型在处理小样本、贫信息及复杂非线性问题等方面具有很大优势,且计算过程与结果均可作出概率解释。该模型方法求得的多项精度指标值均优于BP神经网络方法和GR-SVM方法,证实该方法具有较好的鲁棒性和较强的泛化能力,在隧道地表沉降预测中有较高的精度。
| [1] |
谢家杰. 浅埋隧道的地层压力[J]. 土木工程学报, 1964, 10(6): 58-70 (Xie Jiajie. Formation Pressure of Shallow Tunnel[J]. China Civil Engineering Journal, 1964, 10(6): 58-70)
(  0) 0) |
| [2] |
梅文勇. 双线软岩浅埋隧道施工地表沉降预测及控制[J]. 长沙铁道学院学报, 2003, 21(2): 36-38 (Mei Wenyong. Calculation and Control of Surface Settement in Double-Track Soft Shallow Tunnel[J]. Journal of Changsha Railway University, 2003, 21(2): 36-38 DOI:10.3969/j.issn.1672-7029.2003.02.008)
(  0) 0) |
| [3] |
王源, 刘松玉, 谭跃虎, 等. 九华山隧道爆破施工对明城墙振动影响的监测与分析[J]. 岩土力学与工程学报, 2007, 27(增1): 3 584-3 589 (Wang Yuan, Liu Songyu, Tan Yuehu. Monitoring and Analysis of Ming Dynasty Wall Vibration Influnced by Explosion Construction of Jiuhuashan Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 27(S1): 3 584-3 589)
(  0) 0) |
| [4] |
威纲, 袁曦. 盾构隧道地面长期沉降的时间序列预测[J]. 市政技术, 2008, 26(4): 317-319 (Wei Gang, Yuan Xi. Prediction of Long-Term Surface Settlement Induced by Shield Tunnelling with Time Series Method[J]. Municipal Engineering Technology, 2008, 26(4): 317-319 DOI:10.3969/j.issn.1009-7767.2008.04.017)
(  0) 0) |
| [5] |
刘伟诚, 王青, 高俊强. 基于自适应卡尔曼滤波的沉降变形监测数据估计[J]. 水利与建筑工程学报, 2012, 10(5): 26-29 (Liu Weicheng, Wang Qing, Gao Junqiang. Estimation for Deformation Monitoring Data Based on Adaptive Kalman Filtering Method[J]. Journal of Water Resources and Architectural Engineering, 2012, 10(5): 26-29 DOI:10.3969/j.issn.1672-1144.2012.05.007)
(  0) 0) |
| [6] |
霍玉华. 隧道围岩变形量预测的灰色模型应用比较研究[J]. 北京交通大学学报, 2006, 30(4): 42-45 (Huo Yuhua. Study on the Gray Model and Its Application in Forecasting Deformation of Tunnel Surrounding Rock[J]. Journal of Beijing Jiaotong University, 2006, 30(4): 42-45 DOI:10.3969/j.issn.1673-0291.2006.04.011)
(  0) 0) |
| [7] |
姜德义, 任松, 刘新荣, 等. 隧道拱顶下沉时序遗传算法神经网络预测模型[J]. 地下空间与工程学报, 2006, 2(4): 547-550 (Jiang Deyi, Ren Song, Liu Xinrong, et al. Predicting the Vault Crown Settlement Tendency of Tunnel with the Genetic Neural Network[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(4): 547-550)
(  0) 0) |
| [8] |
潘国荣. 地铁隧道变形的神经网络法预测[J]. 大地测量与地球动力学, 2007, 27(1): 80-84 (Pan Guorong. Deformation Prediction of Subway Tunnel with Neural Network Method[J]. Journal of Geodesy and Geodynamics, 2007, 27(1): 80-84)
(  0) 0) |
| [9] |
胡纪元, 文鸿雁, 周吕, 等. 基于小波神经网络的隧道变形预测模型研究[J]. 公路工程, 2014(4): 26-29 (Hu Jiyuan, Wen Hongyan, Zhou Lü, et al. Research on Prediction Model of Tunnel Deformation Based on Wvelet Neural Network[J]. Highway Engineering, 2014(4): 26-29 DOI:10.3969/j.issn.1674-0610.2014.04.006)
(  0) 0) |
| [10] |
谭鹏, 曹平. 基于灰色关联支持向量机的地表沉降预测[J]. 中南大学学报:自然科学版, 2012, 43(2): 632-637 (Tan Peng, Cao Ping. Predicting Surface Settlement of Tunnel Using Grey Relational-Support Vector Machine[J]. Journal of Central South University(Science and Technology), 2012, 43(2): 632-637)
(  0) 0) |
| [11] |
Tipping M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244
(  0) 0) |
| [12] |
吕峰. 灰色系统关联度之分辨系数的研究[J]. 系统工程理论与实践, 1997, 17(6): 49-54 (Lü Feng. Research on the Identification Coefficient of Relational Grade for Grey System[J]. System Engineering Theory and Application, 1997, 17(6): 49-54 DOI:10.3321/j.issn:1000-6788.1997.06.011)
(  0) 0) |
| [13] |
Zhao W G, Gao Y F, Li C L. RVM Based on PSO for Groundwater Level Forecasting[J]. Journal of Computers, 2012, 7(5): 1 073-1 079
(  0) 0) |
| [14] |
李守巨, 刘应曦, 孙伟. 智能计算与参数反演[M]. 北京: 科学出版社, 2008 (Li Shouju, Liu Yingxi, Sun Wei. Intelligent Calculation and Parameter Inversion[M]. Beijing: Science Press, 2008)
(  0) 0) |
| [15] |
胡坤.灰色预测评价方法与应用研究[D].南京: 南京航空航天大学, 2004 (Hu Kun. Evaluation Method and Its Application Research on Grey Prediction[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2004) http://cdmd.cnki.com.cn/Article/CDMD-10287-2004051570.htm
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37