2. 三峡大学计算机与信息学院,宜昌市大学路8号,443002
滑坡变形预测模型大体上分为两种,一种是确定性模型,即通过力学的方法建立滑坡荷载与滑坡变形之间的力学关系。由于确定性模型需要获取滑坡中一些岩土体的力学参数,而这些参数具有高度的非线性[1-4],难以得到,加之滑坡变形的力学机制比较复杂,要想准确地建立滑坡荷载与滑坡变形之间的力学关系往往十分困难,从而导致确定性模型准确预测滑坡的变形比较困难。另外一种是统计模型,即借助于滑坡变形观测数据,建立时间或环境因素与滑坡变形之间的数学关系式,通过求解相关参数预测滑坡的变形。
滑坡的变形与很多因素密切相关,其中降雨和气温对滑坡的变形影响较为显著。大气降雨对滑坡稳定性的破坏主要表现在降雨除产生坡面径流外,还有相当部分的雨水渗入到滑坡体中,加大了滑坡体的重量,从而增加了滑坡体的下滑力。此外,降雨渗透到滑坡隔水层顶面时,将在这里聚集,使物质软化甚至泥化,降低了滑坡的摩阻力,从而形成滑面或滑带。大气降雨还使坡体中的孔隙水压力增大,从而降低了滑坡体的有效应力,最终导致滑带摩阻力降低。大气温度的变化导致滑坡裂隙的伸缩和变形,从而影响滑坡的稳定性。
考虑到大气降雨和温度会对滑坡的稳定性产生较大的影响,本文将滑坡的变形看作时间、月降雨量、气温的函数,使用泰勒级数建立卡尔曼滤波模型,并用于滑坡变形的预测预报。
1 卡尔曼滤波模型离散线性系统的卡尔曼滤波模型的状态方程和观测方程分别为[5-7]:
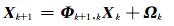
|
(1) |
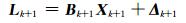
|
(2) |
式中,Xk和Lk分别为tk时刻的状态向量和观测向量,Φk+1, k为tk时刻至tk+1时刻的状态转移矩阵,Bk+1为tk+1时刻的观测矩阵,Ωk和Δk分别为tk时刻的动态噪声和观测噪声。
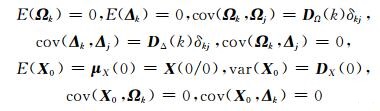
|
(3) |
当j=k时,δkj=1;当j≠k时,δkj=0。
由状态方程、观测方程和随机模型,即可推出如下卡尔曼滤波方程[5-7]:
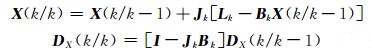
|
(4) |
式中,I为单位矩阵,且
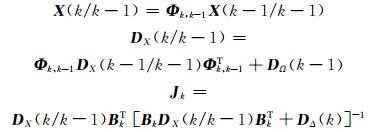
|
(5) |
土质滑坡的变形主要受大气降雨及气温的影响。为此,可以将土质滑坡的变形看作时间、月降雨量和气温的函数,即
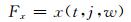
|
(6) |
式中,t为时间(时刻),j为t时刻的月降雨量,w为t时刻的气温,Fx为t时刻滑坡的变形量。
由于滑坡变形观测的时间间隔较短(一般为每月观测一次),且变形量的变化较小,现将tk+1时刻(对应的月降雨量为jk+1、气温为wk+1)的变形量x(tk+1, jk+1, wk+1)在tk时刻用泰勒级数展开,仅取泰勒级数的一次项及二次项得:
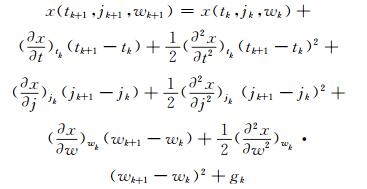
|
(7) |
式中,令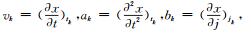
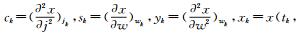
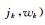
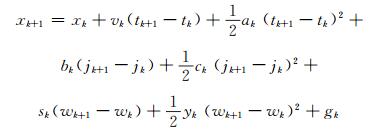
|
(8) |
式中,vk为tk时刻的变形速度,ak为tk时刻的变形加速度,bk为月降雨量的变化对变形的影响,ck为月降雨量的变化的二次方对变形的影响,sk为气温的变化对变形的影响,yk为气温的变化的二次方对变形的影响,gk为泰勒级数的余项,其值微小,可以看作数学期望为0的动态噪声。令
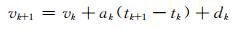
|
(9) |
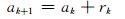
|
(10) |
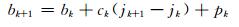
|
(11) |
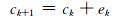
|
(12) |
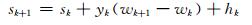
|
(13) |
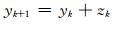
|
(14) |
式中,dk、rk、pk、ek、hk、zk分别为微小的扰动,也可以看作数学期望为0的动态噪声。
将式(8)~(14)写成矩阵形式,得:
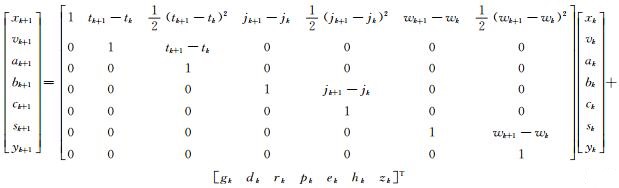
|
(15) |
式中,令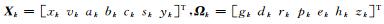
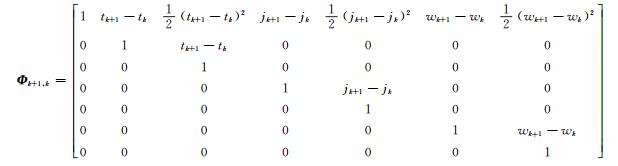
|
则式(15)变为:
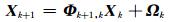
|
(16) |
式(16)即为卡尔曼滤波模型的状态方程。
对于变形观测,有:
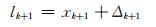
|
(17) |
式中,lk+1为tk+1时刻变形量的观测值,Δk+1为tk+1时刻的观测噪声。令Lk+1为lk+1,Bk+1=[1 0 0 0 0 0 0],则式(17)变为:
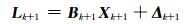
|
(18) |
式(18)即为卡尔曼滤波模型的观测方程。
由状态方程(16)及观测方程(18),并顾及随机模型,由卡尔曼滤波方程即可进行卡尔曼滤波。
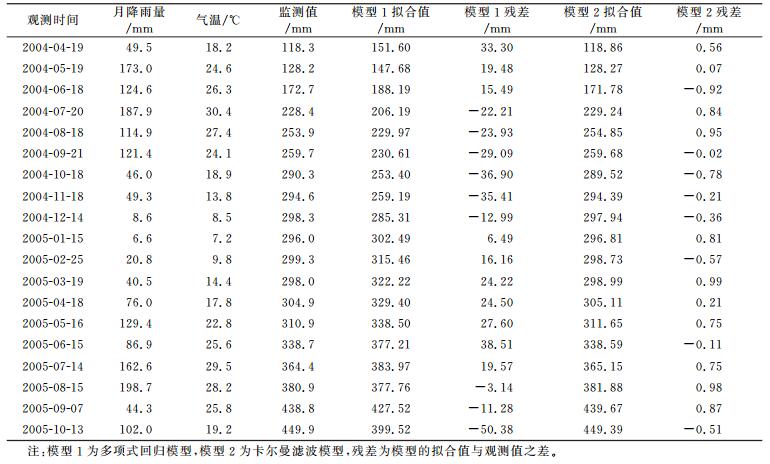
3 算例分析基于上述建模思路,取某滑坡(该滑坡为土质滑坡,且有多条裂隙贯穿该滑坡体)ZG118监测点2004-04~2005-12的水平位移监测资料进行计算(其中2004-04~2005-10的水平位移监测资料用于建模,2005-11及2005-12的水平位移监测资料用于与预测值进行比较),并将计算结果与多项式回归模型(即将变形看作是时间、月降雨量和气温的二次函数建立的模型)进行比较,计算结果见表 1。
|
|
表 1 ZG118点水平位移变形监测值与相应的滤波值 Tab. 1 Horizontal displacement deformation monitoring values and their filter values at ZG118 |
根据变形监测资料分析,水平位移变形监测的中误差(方差)取DΔ(k)=±1 mm,另外,计算时取X (0/0)=[115.4 0 0 0 0 0 0]T,其中,115.4为ZG118点2004-03-15的水平位移变形监测值。状态向量的初始值及动态噪声可以认为是独立不相关的,此时可取:
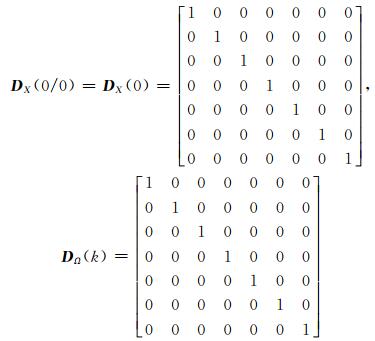
|
相关计算结果见表 1。
由表 1可以看出,当月降雨量增大及气温升高时,ZG118点变形明显增大,表明滑坡变形与月降雨量及气温具有明显的相关性。多项式回归模型残差普遍较大,都超过了3 mm,最大为-50.38 mm,最小为-3.14 mm,大部分残差超过10 mm,表明多项式回归模型的拟合误差较大; 而卡尔曼滤波模型残差普遍较小,都小于1 mm,最大只有0.99 mm,最小只有-0.02 mm,另外,残差的符号有正有负,具有随机性,表明卡尔曼滤波模型的拟合误差较小。多项式回归模型预测2005-11-15和2005-12-15 ZG118点水平位移变形值分别为431.84 mm和445.30 mm,而监测值分别为454.9 mm和463.7 mm,预测误差分别为23.06 mm和18.40 mm。卡尔曼滤波模型预测2005-11-15和2005-12-15 ZG118点水平位移变形值分别为456.20 mm和466.81 mm,预测误差分别为1.30 mm和3.11 mm,表明卡尔曼滤波模型的预测误差小于多项式回归模型。
4 结语由于多项式回归模型将模型的参数作为定值,因此限制了多项式回归模型适应观测数据的能力,从而导致模型的残差较大,拟合效果也不理想,尤其是观测数据较多时更是如此。而卡尔曼滤波模型在卡尔曼滤波的过程中,模型参数不断发生变化,从而提高了其适应观测数据的能力,导致模型的残差较小,拟合效果也较好。
本文考虑到某滑坡的变形主要受大气降雨及气温的影响,以泰勒级数为基础,建立基于时间、月降雨量和气温的卡尔曼滤波模型,并用于滑坡变形的预测预报。实例计算表明,该模型拟合效果和预测效果良好,可用于土质滑坡变形的短期预测预报。
| [1] |
蒋刚, 林鲁生, 刘祖德, 等. 边坡变形的灰色预测模型[J]. 岩土力学, 2000, 21(3): 244-246 (Jiang Gang, Lin Lusheng, Liu Zude, et al. Prediction Grey Model for Slope Displacement[J]. Rock and Soil Mechanics, 2000, 21(3): 244-246 DOI:10.3969/j.issn.1000-7598.2000.03.013)
(  0) 0) |
| [2] |
唐天国, 万星, 刘浩吾. 高边坡安全监测的改进GM模型预测研究[J]. 岩石力学与工程学报, 2005, 24(2): 307-312 (Tang Tianguo, Wan Xing, Liu Haowu. Improved GM Model for Safety Monitoring of High Rock Slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 307-312 DOI:10.3321/j.issn:1000-6915.2005.02.021)
(  0) 0) |
| [3] |
黄志全, 崔江利, 刘汉东. 边坡稳定性预测的混沌神经网络方法[J]. 岩石力学与工程学报, 2004, 23(22): 3 808-3 812 (Huang Zhiquan, Cui Jiangli, Liu Handong. Chaotic Neural Network Method for Slope Stability Prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3 808-3 812)
(  0) 0) |
| [4] |
郑东健, 顾冲时, 吴中如. 边坡变形的多因素时变模型[J]. 岩石力学与工程学报, 2005, 24(22): 3 180-3 184 (Zheng Dongjian, Gu Chongshi, Wu Zhongru. Time Series Evolution Forecasting Model of Slope Deformation Based on Multiple Factors[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 3 180-3 184)
(  0) 0) |
| [5] |
崔希璋, 於宗俦, 陶本澡, 等. 广义测量平差[M]. 北京: 测绘出版社, 1992 (Cui Xizhang, Yu Zongchou, Tao Benzao, et al. General Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 1992)
(  0) 0) |
| [6] |
陆付民, 李劲. 顾及时间和开挖深度的卡尔曼滤波模型在建筑物变形分析中的应用[J]. 测绘通报, 2012(2): 59-61 (Lu Fumin, Li Jin. Application of Kalman Filter Model with the Time and Excavation Depth to Building Deformation Analysis[J]. Bulletin of Surveying and Mapping, 2012(2): 59-61)
(  0) 0) |
| [7] |
周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37-42 (Zhou Letao, Huang Dingfa, Yuan Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 37-42 DOI:10.3321/j.issn:1001-1595.2007.01.007)
(  0) 0) |
2. College of Computer and Information, Three Gorges University, 8 Daxue Road, Yichang 443002, China
 2017, Vol. 37
2017, Vol. 37