2. 西安测绘研究所,西安市雁塔路中段1号,710054;
3. 山东省国土测绘院,济南市经十路2301号,250102
中国大陆地壳运动除了具有明显的整体平移与旋转趋势,在局部区域还存在复杂的非均匀形变。目前,研究地壳运动的方法有两种:1)地球物理模型方法,其能反映长时间的平均形变信息; 2)几何观测方法,即利用GPS等大地测量技术获取高精度地壳形变位移量。国内外学者通常采用欧拉矢量法表示地壳运动趋势,而欧拉矢量法的前提是板块划分可靠且为刚性体[1-2]。但实际上,板块受区域应力及地壳介质差异等多因素影响,呈现复杂的非均匀变形,利用欧亚板块以及二级板块欧拉矢量参数很难真实反映点位实际运动。有学者采用多面函数[3]、有限元插值法[4]、拟合推估法[5]、移动窗口法[2]、综合逼近法[6]、神经网络[1]和混合形变估计法[7]等方法逼近速度场。杨元喜等[7]、赵丽华等[8]充分利用地壳运动的几何观测信息与地球物理信息,提出自适应拟合推估法与自适应滤波方法。神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力,特别适合处理需要同时考虑许多因素和条件的不精确和模糊信息,理论上具有以任意精度逼近连续函数的能力[9],目前已应用于似大地水准面[10]、速度场拟合[1]及组合导航[11]等领域。综合逼近法在统计模型逼近的基础上,利用函数模型进一步逼近速度场模型[6]。本文在前人研究基础上,利用欧拉矢量法估计测站速度,将剩余残差作为Elman神经网络期望输出,利用非线性系统进一步逼近速度场模型,并分析Elman神经网络的适应性。
1 Elman神经网络模型Elman神经网络是一种具有局部记忆单元和局部反馈连锁的BP神经网络结构,其反馈连接是从隐含层的输出到其输入端,这种反馈方式使得Elman神经网络具有探测和识别能力。其隐含层节点有一个与之对应的反馈层节点连接,并且权值可调。反馈层节点的输出实际上起存储网络内部状态的作用,这也是其与BP神经网络的最大区别[12]。
Elman神经网络隐含层的传递函数为tansig函数,设为f1; 输出层的函数为pureline函数,设为f2。隐含层第i个神经元的输出为[12]:
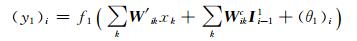
|
(1) |
输出层的第j个输出为:
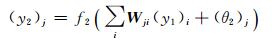
|
(2) |
式中,xk为网络的输入; W′、Wc、W为隐含层、反馈层和输出层的权矩阵; θ1、θ2为阈值; k为迭代次数。
Elman神经网络是基于误差最小原理,目标函数为:
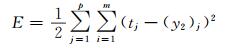
|
(3) |
式中,tj为网络的期望输出; y2为神经网络计算值; p、m分别为输出层、隐含层神经元个数。
隐含层与输出层、隐含层和反馈层的权和阈值的变化量计算方法具体可参考文献[12]。计算过程中,若E不满足限差,根据第k+1次的W′、Wc、W与θ1、θ2,代入式(1)~(3)计算隐含层与输出层的输出、目标函数E,并再次判断,依次循环直至满足要求。
2 基于Elman神经网络的速度场拟合为了有效逼近地壳运动趋势,首先使用欧拉矢量法描述整体趋势,然后再利用拟合推估等方法反映局部形变[7-8]。欧拉矢量法是常用的速度场建模方法,其前提是块体为刚性体。张培震等[13]将中国大陆划分为6个大块体、22个二级块体等; 也有学者提出了不同的二级板块划分方法[14-15]。
欧拉矢量法[1-2]可以整体描述地壳运动趋势,但其残差中仍包含局部地形变信息,而Elman神经网络等拟合方法具有较强的逼近能力,能够在欧拉矢量法整体表示地壳运动的基础上,进一步逼近局部变形信息。
在速度场拟合中,Elman神经网络除了使用拟合点的经纬度(λ, φ)i作为输入向量中的元素外,还可以考虑与拟合点的精度、地质构造差异、断层信息和区域应力等因素,进一步提高拟合的效果。期望输出为拟合点的N、E方向欧拉矢量法的速度残差。在计算过程中,N、E方向单独逼近,不考虑速度之间的相关性; 最后将Elman神经网络计算结果与欧拉矢量法计算速度相叠加,获取各点的最终拟合速度。基于Elman神经网络的速度场拟合流程如图 1所示。

|
图 1 基于Elman神经网络的速度场拟合流程 Fig. 1 The flow chart of velocity field fitting based on Elman neural network |
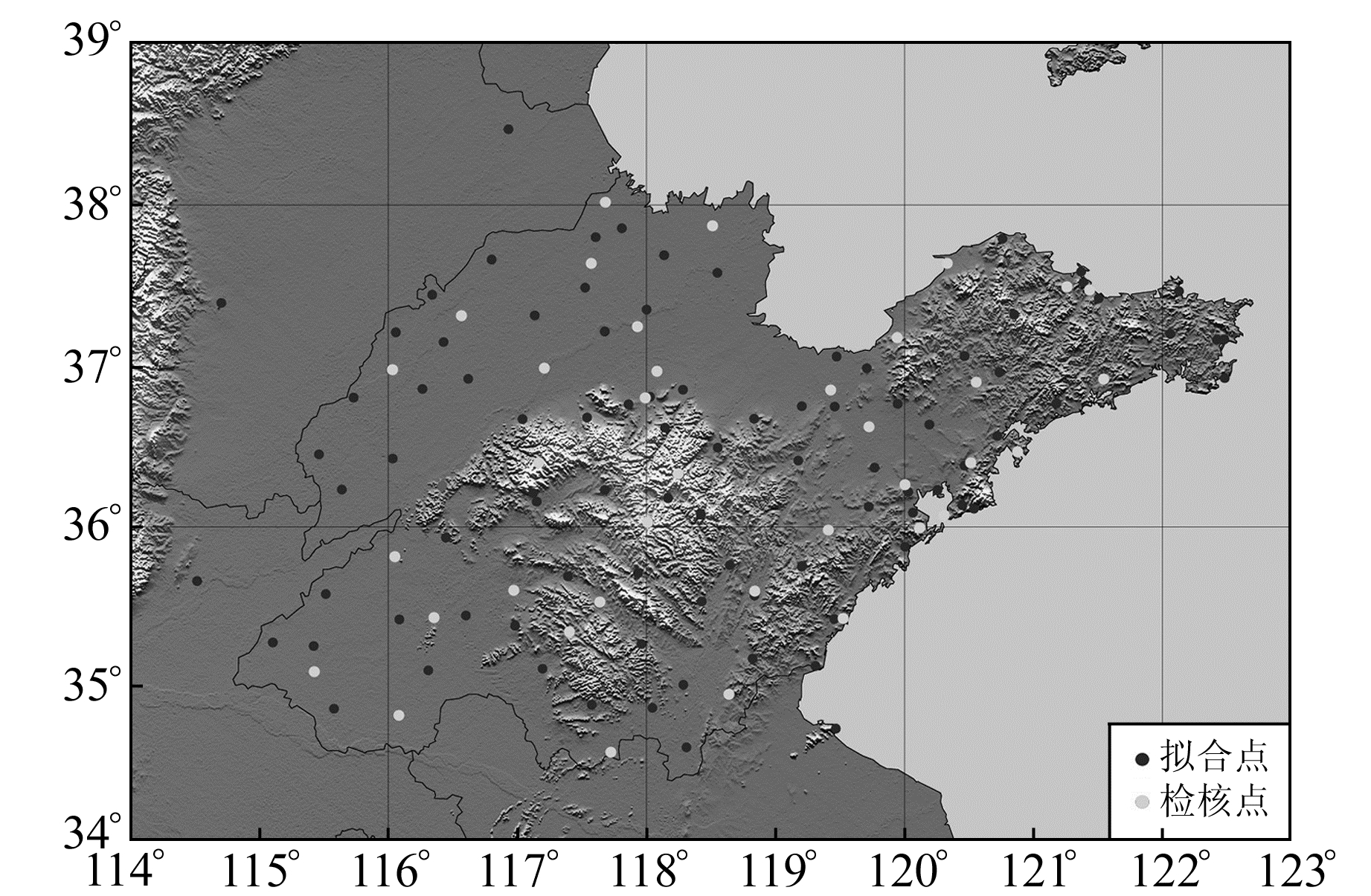
收集山东省135个CORS站2010~2015年连续观测数据,使用GAMIT/GLOBK软件获取山东省CORS站速度,经检验分析剔除2个异常点。利用剩余133个CORS点的速度成果,分析Elman神经网络方法在速度场拟合中的适用性,计算过程中均匀选择95个站点作为拟合点,38个站点作为外部检核点(图 2)。
|
图 2 拟合点与检核点分布 Fig. 2 The distribution of fitting points and check points |
在已有欧拉矢量法估计的基础上,利用Elman神经网络分别逼近E、N方向速度差值。其中Elman神经网络采用单隐含层; 输入向量为站点经纬度; 期望输出为E、N方向的速度差值; 输入层与输出层节点分别为2、1,隐含层节点取10;隐含层与输入层之间采用sigmoid函数,输出层与隐含层之间的传递函数为线性传递函数purelin函数; 神经网络采用traingdx函数,最大训练历元为50 000,训练要求精度为0.000 01。采用8种方案进行验证:
1) 利用NNR_NUVEL1A模型[2]欧拉矢量参数估计速度; 2)在方案1的基础上,利用最小二乘配置方法[7, 15]进一步逼近; 3)在方案1的基础上,利用自适应最小二乘配置方法[7, 15]进一步逼近; 4)在方案1的基础上,利用Elman神经网络进一步逼近; 5)利用华北平原二级板块欧拉矢量参数[14]估计速度; 6)在方案3的基础上,利用Elman神经网络进一步逼近; 7)根据文献[14]中欧拉矢量的计算方法,利用山东省CORS站数据计算山东省局部欧拉矢量参数,并得到的局部欧拉矢量参数估计所有点速度; 8)在方案5的基础上,利用Elman神经网络进一步逼近。计算结果见表 1,误差曲线见图 3~6。
|
|
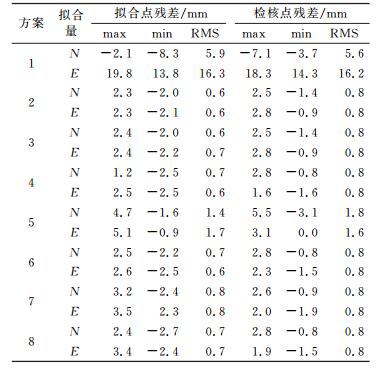
表 1 速度场拟合结果精度统计 Tab. 1 The accuracy statistic of velocity field fitting model |
|
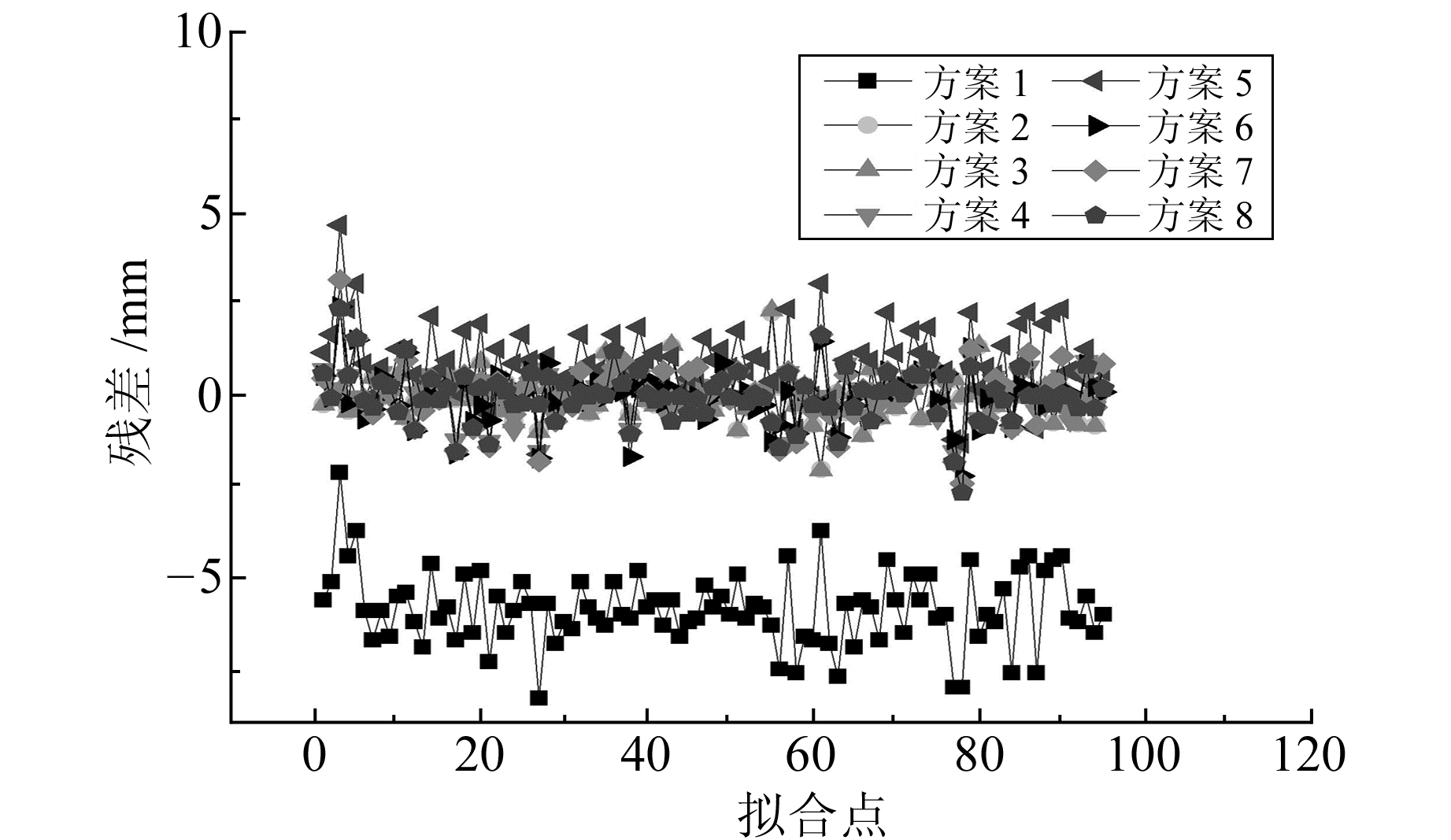
图 3 N方向拟合点残差 Fig. 3 The N direction residual graph of fitting points |
|
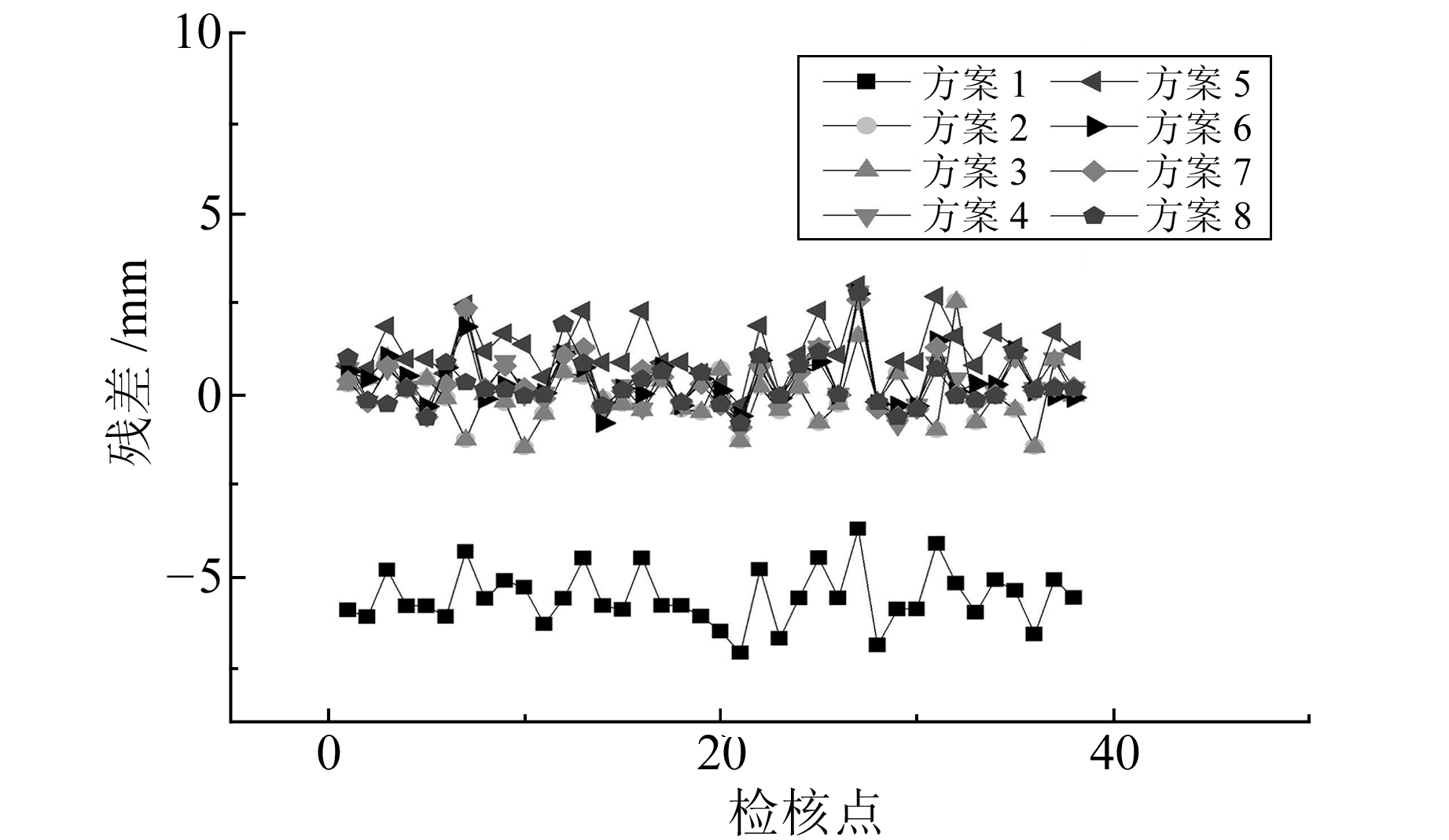
图 4 N方向检核点残差 Fig. 4 The N direction residual graph of checking points |
|
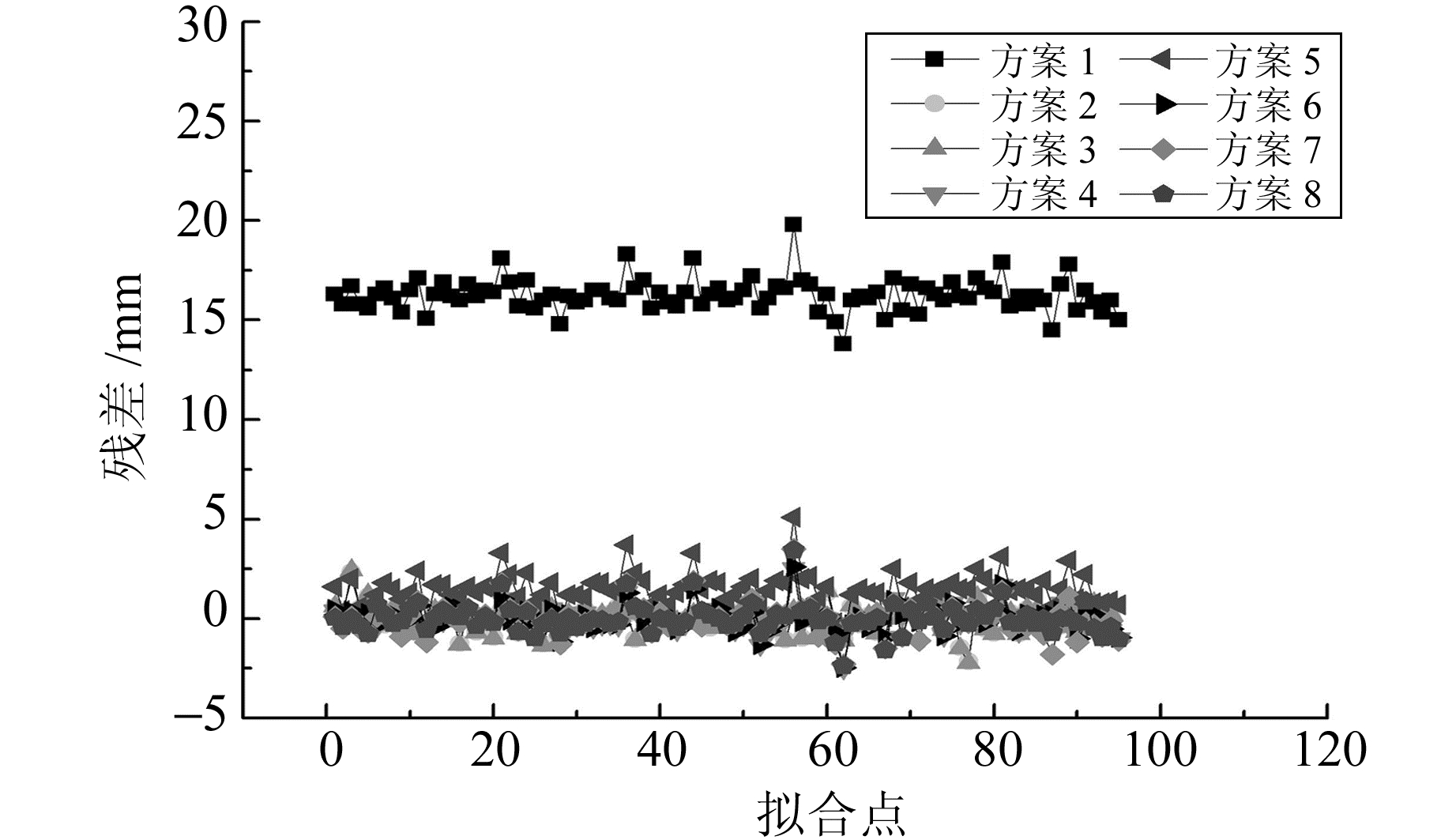
图 5 E方向拟合点残差 Fig. 5 The E direction residual graph of fitting points |
|
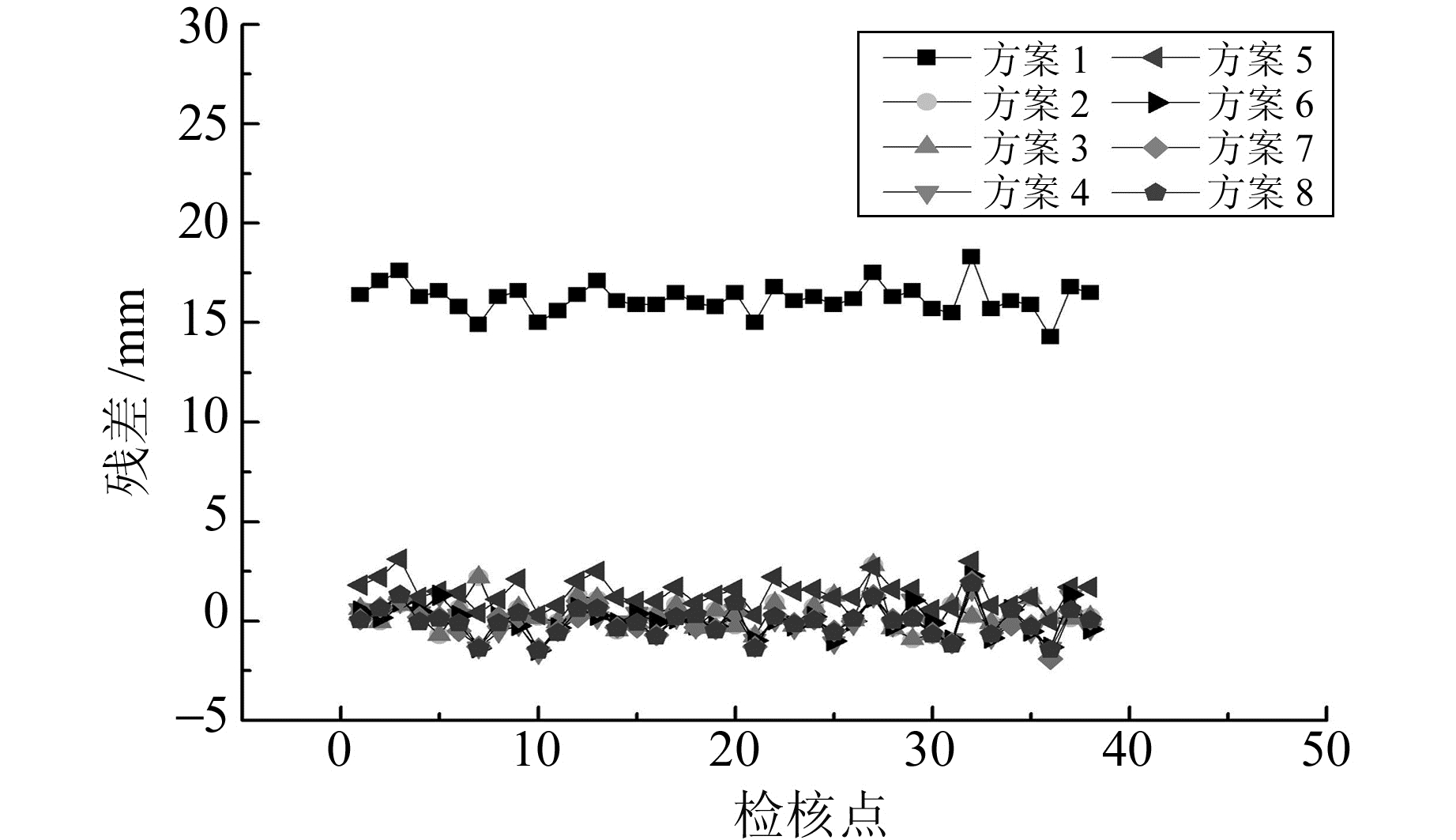
图 6 E方向检核点残差 Fig. 6 The E direction residual graph of checking points |
由以上计算结果可以得到如下结论:
1) 利用山东CORS站估计的欧拉矢量参数所得到的速度结果与利用欧亚板块、华北平原欧拉矢量参数计算的站点速度存在一定差异, 其中N方向拟合精度分别为5.9 mm、1.4 mm、0.8 mm,N方向检核精度分别为5.6 mm、1.8 mm、0.8 mm,E方向拟合精度分别为16.3 mm、1.7 mm、0.8 mm,E方向检核精度分别为16.2 mm、1.6 mm、0.8 mm。其原因是方案7的欧拉矢量参数能够更真实可靠地反映山东省区域的板块运动趋势,而方案1、5的欧拉矢量参数在该区域适用性稍差。
2) 在扣除欧拉矢量估计速度的基础上,Elman神经网络的非线性系统理论上能够无限逼近,提高拟合精度。图 3~6中,方案4、6与方案1、5相比,拟合精度与检核精度有不同程度的提高,如Elman神经网络的N、E方向拟合、检核精度不大于0.8 mm,而方案1、5的N、E方向拟合、检核精度不小于1.4 mm。其原因是方案1、3拟合残差中还存在一定的线性与非线性趋势项,采用Elman神经网络能够进一步削弱趋势项影响; 方案2、3与方案4的N、E方向拟合、检核精度相当,这也证明了Elman神经网络与最小二乘配置方法一样,具有抑制信号影响的作用; 方案8与方案7的各方向拟合、检核精度相当,说明了Elman神经网络与局部逼近函数具有相同的逼近能力。
3) 比较方案4、6、8可知,Elman神经网络的N、E方向拟合精度与检核精度一致,量级在0.8 mm左右,这从另一方面证明了神经网络具有较强的非线性函数映射能力,能够提高计算精度,但这种逼近效果的提高是有限度的,不能完全实现理论上的无限逼近。Elman神经网络具有反馈层,可以存储前一次的数值,并应用于本次计算,不但可以学习空间模式,也可以学习时间模式,这是其与BP神经网络的区别。但Elman神经网络存在容易陷入局部极小值、结果随机性强、训练函数与学习效率等参数选取依靠经验等缺点,在一定程度上限制了其在速度场逼近的进一步推广应用。
4 结语地壳运动模型是大地基准维护、地球动力学等工程与学科的重要基础模型,合理有效的拟合与插值方法是提高区域速度场的精度与可靠性的重要因素。本文在利用欧拉矢量法扣除趋势项的基础上,充分利用Elman神经网络能够进一步增强速度场逼近效果,削弱数据中系统误差及其他不确定因素影响,提高速度场的拟合精度。但Elman神经网络也具有神经网络的缺陷,这影响其在速度场拟合中的进一步应用。
致谢: 感谢山东省国土测绘院与陆态网络中心提供的观测数据。
| [1] |
李冲, 李建成, 黄瑞金, 等. 考虑欧拉矢量的BP神经网络模型建立区域地壳运动速率场[J]. 武汉大学学报:信息科学版, 2014, 39(3): 362-366 (Li Chong, Li Jiancheng, Huang Ruijin, et al. Building up Regional Crustal Movement Velocity Field with BP Neural Network Base on Euler Vector[J]. Geomatics and Information Science of Wuhan University, 2014, 39(3): 362-366)
(  0) 0) |
| [2] |
吴富梅, 刘光明, 魏子卿. 利用局域欧拉矢量法建立CGCS2000速度场模型[J]. 武汉大学学报:信息科学版, 2012, 37(4): 432-435 (Wu Fumei, Liu Guangming, Wei Ziqing. Velocity Field Model of CGCS2000 Based on Euler Vector of Local Area[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 432-435)
(  0) 0) |
| [3] |
刘经南, 姚宜斌, 施闯. 中国地壳运动整体速度场模型的建立方法研究[J]. 武汉大学学报:信息科学版, 2002, 27(4): 331-336 (Liu Jingnan, Yao Yibin, Shi Chuang. Method for Establishing the Speed Field Model of Crustal Movement in China[J]. Geomatics and Information Science of Wuhan University, 2002, 27(4): 331-336)
(  0) 0) |
| [4] |
蒋志浩, 张鹏, 秘金钟, 等. 基于CGCS2000的中国地壳水平运动速度场模型研究[J]. 测绘学报, 2009, 38(6): 471-476 (Jiang Zhihao, Zhang Peng, Bei Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 471-476 DOI:10.3321/j.issn:1001-1595.2009.06.001)
(  0) 0) |
| [5] |
江在森, 刘经南. 应用最小二乘配置建立地壳运动速度场与应变场的方法[J]. 地球物理学报, 2010, 53(5): 1 109-1 117 (Jiang Zaisen, Liu Jingnan. The Method in Establishing Strain Field and Velocity Field of Crustal Movement Using Least Squares Collocation[J]. Chinese J Geophys, 2010, 53(5): 1 109-1 117)
(  0) 0) |
| [6] |
刁法启, 熊熊. 地壳运动速度场插值方法研究[J]. 武汉大学学报:信息科学版, 2008, 33(6): 627-630 (Diao Faqi, Xiong Xiong. Interpolation Approach for Velocity Field of Crustal Movement[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 627-630)
(  0) 0) |
| [7] |
杨元喜, 曾安敏. 顾及几何观测信息和地球物理模型的形变参数自适应滤波解[J]. 中国科学:地球科学, 2009, 39(4): 437-442 (Yang Yuanxi, Zeng Anmin. Adaptive Filtering for Deformation Parameter Estimation in Consideration of Geometrical Measurements and Geophysical Models[J]. Science China Earth Sciences, 2009, 39(4): 437-442)
(  0) 0) |
| [8] |
赵丽华, 杨元喜. 综合地球物理信息与几何观测量的地壳形变分析方法[J]. 武汉大学学报:信息科学版, 2009, 34(9): 1 090-1 093 (Zhao Lihua, Yang Yuanxi. Crustal Deformation Analysis of Combined Geophysical Information with Geodetic Measurements[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 090-1 093)
(  0) 0) |
| [9] |
杨建刚. 人工神经网络使用教程[M]. 杭州: 浙江大学出版社, 2001 (Yang Jiangang. Artificial Neural Network Tutorial[M]. Hangzhou: Zhejiang University Press, 2001)
(  0) 0) |
| [10] |
郭春喜, 聂建亮, 王斌, 等. 利用自适应最小二乘配置的GPS水准与重力似大地水准面的拟合[J]. 武汉大学学报:信息科学版, 2013, 38(1): 44-47 (Guo Chunxi, Nie Jianliang, Wang Bin, et al. The Fitting of GPS-Level and Gravity Quasigeoid Based on Adaptive Collocation[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 44-47)
(  0) 0) |
| [11] |
吴富梅, 聂建亮, 董海静. 基于Elman神经网络和Kalman滤波的捷联惯导精对准[J]. 中国惯性技术学报, 2006, 14(5): 9-13 (Wu Fumei, Nie Jianliang, Dong Haijing. SINS Refined Initial Alignment Based on Elman Neural Network and Kalman Filtering[J]. Journal of Chinese Inertial Technology, 2006, 14(5): 9-13 DOI:10.3969/j.issn.1005-6734.2006.05.003)
(  0) 0) |
| [12] |
聂建亮.神经网络及其在大地测量数据处理中的应用[D].西安: 长安大学, 2007 (Nie Jianliang.Neural Networks and Its Applications in Processing of Data of Geodesy[D]. Xi'an: Chang'an University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-11941-2009257155.htm
(  0) 0) |
| [13] |
张培震, 邓起东, 张国民, 等. 中国大陆的强震活动与活动地块[J]. 中国科学:D辑, 2003, 33(增1): 12-20 (Zhang Peizhen, Deng Qidong, Zhang Guomin, et al. Active Tectonic Blocks and Strong Earthquakes in the Continent of China[J]. Science in China:Ser D, 2003, 33(S1): 12-20)
(  0) 0) |
| [14] |
魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系:中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410 (Wei Ziqing, Liu Guangming, Wu Fumei. China Geodetic Coordinate System 2000:Velocity Field in Mainland China[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 403-410)
(  0) 0) |
| [15] |
程鹏飞, 成英燕, 秘金钟, 等. CGCS2000板块模型构建[J]. 测绘学报, 2013, 42(2): 159-167 (Cheng Pengfei, Cheng Yingyan, Bei Jinzhong, et al. CGCS2000 Plate Motion Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 159-167)
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Institute of Land Surveying and Mapping of Shandong Province, 2301 Jingshi Road, Ji'nan 250102, China
 2017, Vol. 37
2017, Vol. 37